复平面上正多边形的判定及应用
2016-01-28蒋巧云袁邢华
蒋巧云, 袁邢华
(南通大学理学院,江苏南通226007)
复平面上正多边形的判定及应用
蒋巧云,袁邢华
(南通大学理学院,江苏南通226007)
[摘要]结合教学给出复平面上n个点成为正多边形的条件,最后讨论它的一些应用.
[关键词]复平面; 正多边形; n次方根
1引言
设z为复数,n为正整数,方程ωn=z的任一解称为z的一个n次方根,其全部n次方根为

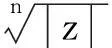
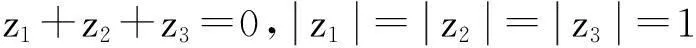
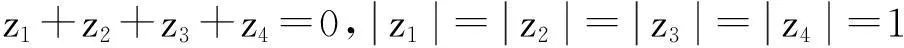
本文在第二部分先讨论一般情况,对于复平面上n(n≥3)个点z1,z2,…,zn,在哪些条件下可以保证n(n≥3)个点z1,z2,…,zn是内接于圆的一个正n边形的顶点.然后讨论当n=4和n=5时的情况,给出另外一个形式的等价条件.
在本文的第三部分简单讨论它的一些应用.
希望通过本文的讨论,在今后的教学过程中更加全面深入的讲解这部分知识,激发学生的学习兴趣,帮助学生更好地理解和掌握相关的内容.
2主要结果与证明
在这部分,先给出如下记号:设复平面上n(n≥3)个点z1,z2,…,zn,令



(1)
则z1,z2,…,zn是中心在原点的正n边形的n个顶点.
证由于z1,z2,…,zn是n次多项式
f(z)=(z-z1)(z-z2)…(z-zn)=zn-T1zn-1+T2zn-2-…+(-1)n-1Tn-1z+(-1)nTn
的根.


f(z)=zn+(-1)nTn=zn+(-1)nz1·z2·…·zn,
即z1,z2,…,zn是方程zn=(-1)n-1z1·z2·…·zn的n个根. 由引言知,这n个复数根均匀的分布在以原点为中心的正n边形的顶点上.
定理2对于复平面上四个点z1,z2,z3,z4,如果满足条件
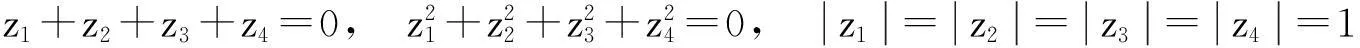
则z1,z2,z3,z4是内接于单位圆的一个正四边形的顶点.
证由于z1,z2,z3,zn是4次多项式
f(z)=(z-z1)(z-z2)(z-z3)(z-z4)=z4-T1z3+T2z2-T3z+T4

知T2=0.再由定理1知z1,z2,z3,z4是内接于单位圆的一个正四边形的顶点.
定理3对于复平面上五个点z1,z2,z3,z4,z5,如果满足条件
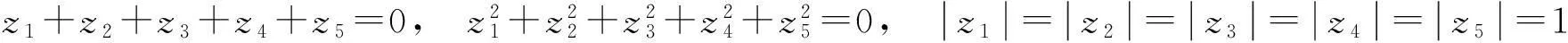
则z1,z2,z3,z4,z5是内接于单位圆的一个正五边形的顶点.
证由于z1,z2,z3,z4,z5是5次多项式
f(z)=(z-z1)(z-z2)(z-z3)(z-z4)(z-z5)=z5-T1z4+T2z3-T3z2+T4z-T5


例判断以下几组点是否构成正多边形:

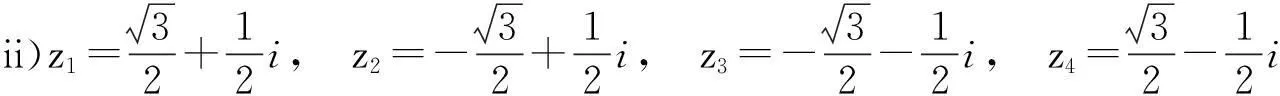
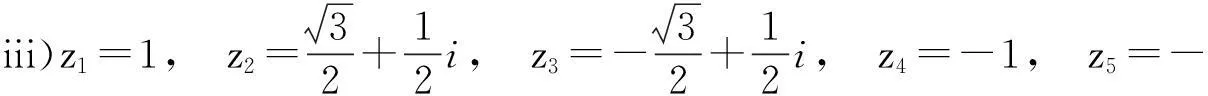
解i) 经计算

故z1,z2,z3,z4是内接于单位圆的一个正四边形的顶点.
3应用
在这部分中我们讨论对于给定的多项式如何判断它的根是否可以构成一个正多边形.
设f(z)=zn+a1zn-1+a2zn-2+…+an-1z+an的n个复根为z1,z2,…,zn,由根与系数的关系知z1+z2+…+zn=-a1. 而由z1,z2,…,zn组成的多边形的中心
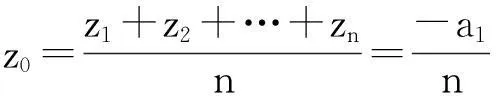
g(z)=zn+a′1zn-1+a′2zn-2+…+a′n-1z+a′n.
若a′k=0,k=1,2,…,n-1,a′n≠0则原多项式的n个复根z1,z2,…,zn构成一个正n边形,否则不能.
例不求方程的根,判断下列多项式的根是否可以构成一个正多边形
i)f1(z)=z4+4z3+6z2+4z+2;
ii)f2(z)=z5-5z4+10z3-10z2+6z+1.
解i) 由于f1(z)的四个根组成的四边形的中心为-1,故经过坐标平移后
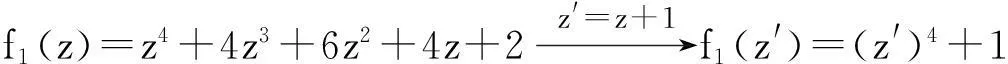
故f1(z)的四个根构成一个正四边形
ii) 由于f2(z)的五个根组成的四边形的中心为1,故经过坐标平移后
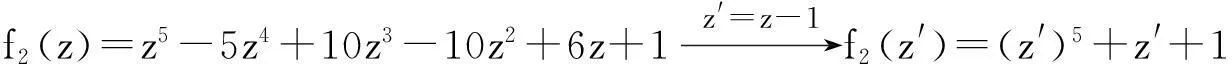
故f2(z)的五个根不能构成一个正五边形.
[参考文献]
[1]钟玉泉. 复变函数论[M]. 3版. 北京:高等教育出版社, 2004.
[2]余家荣. 复变函数论[M]. 3版. 北京:高等教育出版社, 2000.
[3]路见可,钟可寿,等. 复变函数论. (第二版)[M]. 2版. 武汉:武汉大学出版社, 2007.
The Decision to Regular Polygons in Complex Plane and Application
JIANGQiao-yun,YUANXing-hua
(College of Science, Nantong University, Nantong,Jiangsu 226007, China)
Abstract:Connect with teaching we give the condition to n-pionts be a regular polygons in Complex plane and talk about the application.
Key words:complex plane; regular polygons; n-th root
[基金项目]南通大学教学改革课题(2014B7)
[收稿日期]2011-04-22
[中图分类号]O174.5
[文献标识码]C
[文章编号]1672-1454(2015)01-0113-03
