积分变换中常见问题

滕岩梅

(北京航空航天大学数学与系统科学学院，北京100190)



积分变换中常见问题

滕岩梅

(北京航空航天大学数学与系统科学学院，北京100190)

[摘要]积分变换是工科基础课程，具有公式多、难度大、应用广泛的特点.本文对积分变换中教师和学生易忽略问题进行了归纳总结，并举出大量例子.

[关键词]傅立叶变换； 拉普拉斯变换； 广义积分

1引言

积分变换课程是许多工科院系必修的一门课程，具有公式多、计算量大等特点，它对后继课程的学习至关重要，在物理、通讯、图像处理、统计等领域均有着广泛应用.

学生在学习积分变换时多数会感觉有些吃力，公式较多且容易混淆，不容易记忆是一方面的原因；另外积分变换中有一些容易忽略问题，导致错误发生，在讲授积分变换时，也要求教师特别留意.

2积分变换中要注意的问题

1.1　古典傅立叶变换之前提

例1求函数e-2it的傅立叶变换.

按反常积分来计算

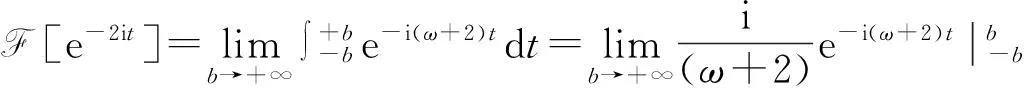
发现此积分无法计算.此种计算方法没有注意到函数e-2it不满足古典傅立叶变换要求的绝对可积条件，它的古典傅立叶变换是不存在的.这时应考虑其广义傅立叶变换.

方法2. 因为

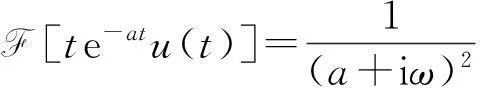
令a=0，则

方法2是错误的，这是因为尽管a>0时，te-atu(t)是绝对可积的，但在a→0的过程中，te-atu(t)收敛的速度越来越慢，以至于当a=0时，te-atu(t)不再绝对收敛.

1.2　关于δ(t)函数

δ(t)函数即为工程中的单位脉冲函数，在工程上，它非常易描述，很直观，学生很好理解.如果用准确的数学语言来描述其本质，对没有学习过弱拓扑的工科学生来说，比较晦涩难懂. 这时，一方面尽量把与δ(t)函数相关问题用工程语言来解释，并注意它的筛选性质；另一方面，强调量化计算时，δ(t)函数作为一个抽象的函数，不能直接运算，而考虑用弱极限的运算来替换.

例3求函数sin2t的傅立叶变换.

表面看起来，这是两个不同结果，而所用两种方法均是正确的，似乎出现奇怪现象.实际上，这两个结果是相等的，可以按δ(t)函数的数学定义或筛选性质来验证.

另外，在验证广义傅立叶变换的积分性质等一些问题时也用到了这一思想[2].

例4求函数δ(t)et的拉普拉斯变换.

解

1.3　性质使用不准确

用积分变换性质计算函数傅立叶变换，有时会出现用不同方法，所得结果完全不同的现象.这也是学生经常感到疑惑的地方.

例5求函数tf(-2t)的傅立叶变换.

解方法1.

方法2.

这两种方法哪种是正确的呢？可以用傅立叶变换的定义来检验.

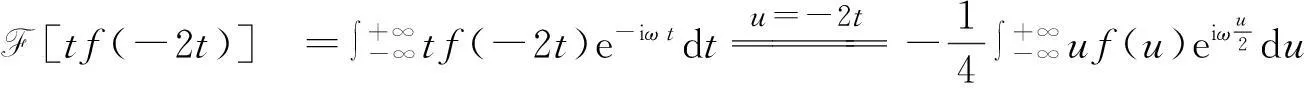
方法1对傅立叶变换的微分性质使用不正确.应对f(-2t)的傅立叶变换求导，它是关于ω的复合函数.

解方法1.

方法2.

方法3.

这里，方法2是错误的，这是用位移性质求积分变换常见问题，一定要注意关于s函数如何赋值问题，必要时用定义检验.

1.4　性质使用时没有注意要求的条件

例如拉普拉斯的延迟性质：

L [f(t-τ)u(t-τ)]=e-sτL [f(t)]，

在使用时要注意公式中的u(t-τ)条件，此条件也可以替换为t<0时，f(t)=0.

例7求下列函数的拉普拉斯变换: (i) sin(t-π)u(t-π); (ii) sin(t-π).

例8求函数f(t)=(t-1)2et的拉普拉斯变换.

方法2. L [(t-1)2et]=L [(t2-2t+1)et]=L [t2et]-2 L [tet]+L [et]

方法1错误的使用了延迟性质，忽视了延迟性质中当t<0时，f(t)=0的要求.

1.5　常见的不能用留数方法求拉普拉斯逆变换情况

例8用拉普拉斯变换求解微分方程

y″+3y′+2y=u(t-1)，y(0)=0，y′(0)=1.

解方法1.设y(s)是y(t)的拉普拉斯变换

第一步：两边求拉氏变换得

第二步：整理得

第三步：求拉普拉斯逆变换

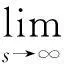
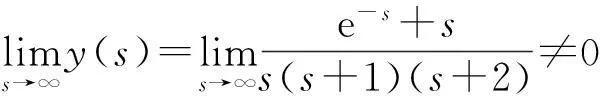
方法2.

第一步：两边求拉氏变换得

第二步：整理得

第三步：求拉普拉斯逆变换

两边进行拉氏逆变换，由延迟性质得

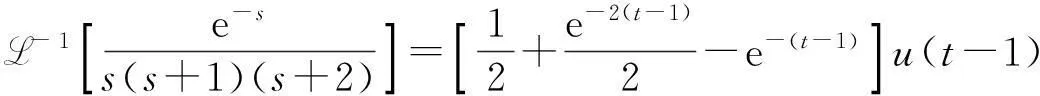
而

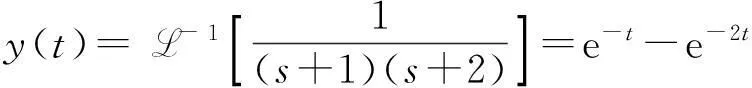
方法2.

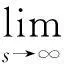
1.6　求分段函数的拉普拉斯变换

例10用拉普拉斯变换求解微分方程

其中y(0)=0，y′(0)=1.

解方法1. 当t<1时，两边进行拉氏变换得

s2y(s)-1+3sy(s)+2y(s)=0，

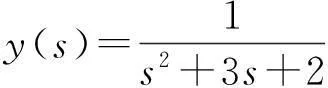
因此

=e-t-e-2t.

当t>1时，两边进行拉氏变换得

整理得

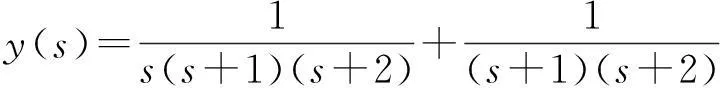
求拉普拉斯逆变换得

方法2. 方程两边同时进行拉普拉斯变换得

整理得

求拉普拉斯逆变换得

例11[3]利用拉普拉斯变换求解微分方程

其中y(0)=0，y′(0)=0.

解方程两边同时进行拉普拉斯变换得

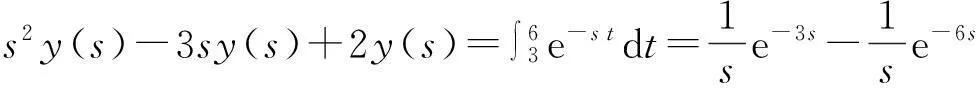
整理得

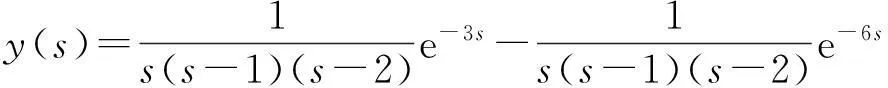
求拉普拉斯逆变换得

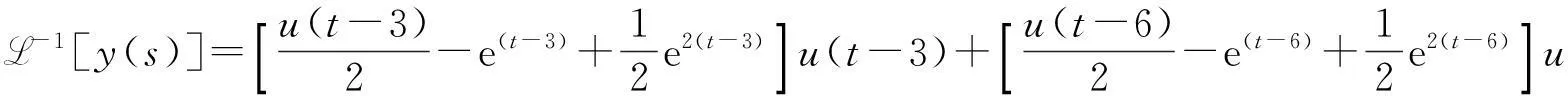
3 结 论

从上述几个问题中可以看到， 有的结果与准确的结果只有极小的差异， 但绝不是计算上的粗心， 而是根本思路上的错误， 为了避免出现类似的情况， 在使用定义， 性质及定理时， 要注意其包含的条件及采用的方法.

[参考文献]

[1]宋琪，容太平.有关傅立叶变换和傅立叶系数求解的有关问题[J].电气电子教学学报，2000，22(3)：40-42.

[2]高宗升，滕岩梅.复变函数与积分变换[M]. 5版.北京航空航天大学出版社， 2010.

[3]Saff E B. Snider AD. Fundamentals of Complex Analysis With Applicationsto Engineering and Science[M]. 3rd Ed. Beijing: China Machine Press， 2005.

Some Problems in Integeral Transform

TENGYan-mei

(School of Mathematics and Systems Science， Beihang University， Beijing 100191， China)

Abstract:Integral transform is fundamental curriculum of higher engineer colledge and has the character of more figure，difficult and widely used. In this paper， we summarize the problems that the teachers and the students easily ignored and some examples are given.

Key words:Fourier transform; Laplace transform

[基金项目]北京航空航天大学校重点教改项目(201413)

[收稿日期]2014-05-15；[修改日期]2015-01-23

[中图分类号]O177.6

[文献标识码]C

[文章编号]1672-1454(2015)01-0105-05