基于极坐标增强的齿轮早期点蚀故障诊断

杨青乐， 张玲玲， 贾继德， 梅检民， 耿　帅

(军事交通学院 军用车辆系，天津　300161)



基于极坐标增强的齿轮早期点蚀故障诊断

杨青乐， 张玲玲， 贾继德， 梅检民， 耿帅

(军事交通学院 军用车辆系，天津300161)

齿轮在机械传动系统中应用广泛，发生故障时将严重影响安全性与可靠性，故对齿轮进行故障诊断具有重要意义。变速器齿轮发生点蚀故障时，其振幅随故障的恶化而加大，并且工作中的冲击将使得振动信号呈现非平稳时变特性。目前，对变速箱故障诊断的方法有多种，由于利用振动信号携带的运行状态信息进行故障诊断可不拆解变速箱，并且振动理论成熟，测量方便，因而得到越来越多的应用[1-4]。

变速器齿轮早期点蚀故障特征十分微弱，在噪声和其他信号干扰下较难被检测与发现，如何有效提取早期微弱故障特征是研究的难点[5-6]。小波分析是一种非平稳信号分析的有效方法，能够将信号的瞬态特征在二维时-频平面上展现出来，但是对于齿轮早期微弱点蚀故障引起的周期性瞬态特征，由于故障引起的振动持续时间短，能量增加不显著，导致周期瞬态冲击特征在直角坐标系下的时频图上反映不明显；相对直角坐标时频分布，极坐标通过极角和极径的表示方法可以形象、直观地将旋转设备振动信号的周期性表现出来，在工程实践中更容易被工程技术人员理解与掌握[7]。

本文提出了一种极坐标增强小波时频图的角频分布方法：首先对信号进行连续小波变换得到瞬态特征的时频分布；然后将直角坐标系的时频分布映射为极坐标系角频分布；最后叠加不同周期的极坐标系角频分布到同一极坐标上，增强点蚀故障引起的周期瞬态冲击。仿真信号和应用实例表明，极坐标增强方法可以有效突出故障信号特征，准确诊断出齿轮早期微弱点蚀故障。

1极坐标增强小波时频图原理

1.1连续小波变换

具有有限能量的函数x(t)∈L2(R)的连续小波变换定义为：

(1)

式中：

(2)

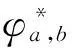
由于小波在频域具有带通特性，其中心频率为f0，在不同尺度a下带通滤波器的中心频率为f0/a，而尺度a、频率f和采样频率fs满足如下关系式：

f=f0×fs/a

(3)

则连续小波变换公式(1)可以重新定义为：

Cx(f,b)=

(4)

式中：Cx(f,b)为小波变换系数，反映了信号通过小波变换后的时频分布。

对信号作小波变换处理时，最重要的是寻找适当的小波基函数作母函数。一般可依照小波基函数的属性、被检信号的特征和所作分析的具体要求选取最佳的小波基函数，齿轮点蚀故障振动信号为冲击型信号，本文选取Morlet小波作为基小波。

1.2极坐标增强小波时频图

如果信号x(t)中存在周期性的且具有相同频率特性的瞬态成分，则小波变换将这些瞬态成分在时频平面上表现为：相对于等时间轴间隔，频率轴同样频宽的区域会出现相似的能量分布。设Cx(f,b)是时频平面的连续小波变换系数, 对于信号x(t)的不同周期Ti, 令：

(5)

由连续小波变换的线性性质可知，Cx(f,b)存在周期为Ti的成分,将存在周期为Ti成分的小波变换系数Cx(f,b)按照式(5)进行坐标转换并累加到同一极坐标图中, 则信号x(t)中周期为Ti的瞬态特征在极坐标上映射为同一角位置，且该处系数等于各个周期系数绝对值之和，从而信号周期性特征在极坐标系上得到增强。

2仿真分析

构造仿真信号x(t)，包含周期性冲击信号和白噪声，表达式为：

(6)

式(6)中载波频率fn=3 000 Hz，位移常数x0=3，阻尼系数ξ=0.1，冲击故障发生的周期T=0.02 s，采样频率fs=20 kHz，采样点数N=4 096，t为采样时刻，n(t)为功率为1的白噪声。

仿真信号的时域波形图和连续小波变换时频分布分别如图1、图2所示。由于噪声影响，时域波形图中冲击成分难以辨识，经过连续小波变换，时频图中周期性冲击特征能够初步识别出来。

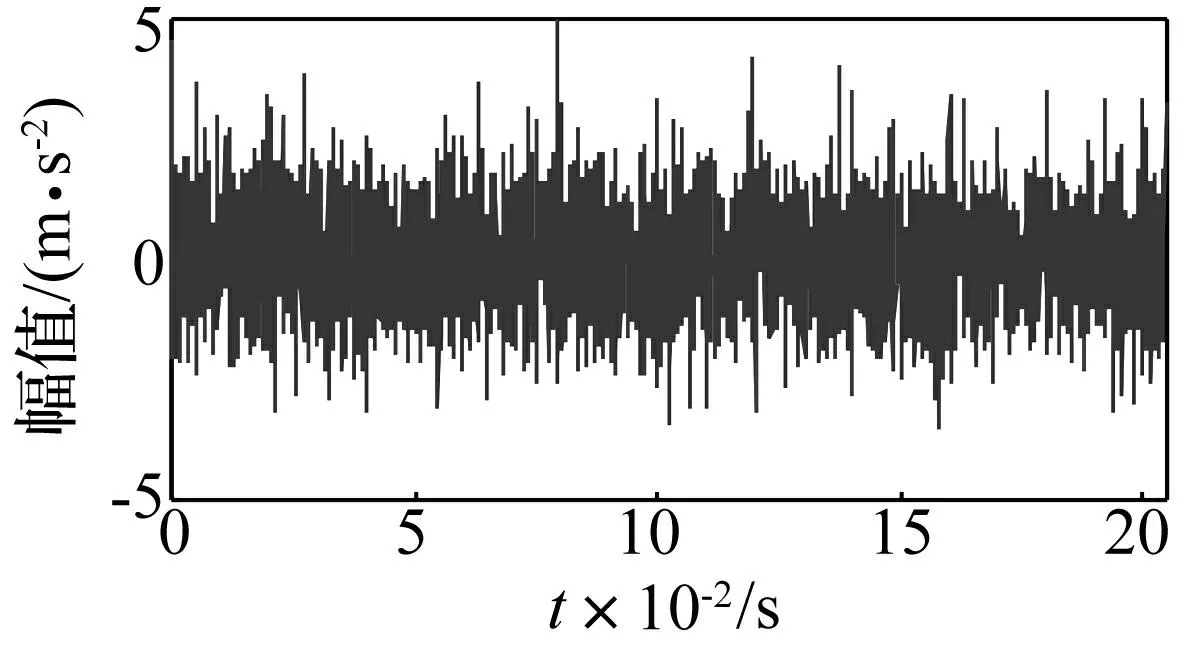
图1　仿真信号时域波形Fig.1 Time domain waveform of simulation signal

图2　仿真信号时频分布图Fig.2 Time-frequency distribution of simulation signal

图3　仿真信号单周期极坐标角频分布图Fig.3 Polar diagram angle frequency distribution of single cycle

按照式(4)、(5)对信号x(t)连续10个周期Ti(i=1,2,3,…,10)的数据分别进行极坐标角频分布表示，极角对应采样时间，沿圆周逆时针方向映射时频分布。极径与频率相对应，5个极径分别对应频率0.8、1.6、2.4、3.2、4 kHz。

周期T5、T6、T7(篇幅限制，仅选取三个周期)的极坐标角频分布如图3，图中每个周期的冲击成分集中在极坐标[0°,3 kHz]附近，但冲击能量较微弱，特征表现不明显。将10个周期极坐标角频分布叠加到一个极坐标系下，结果如图4所示，对比图3(a)~(c)可以看出，瞬态冲击成分明显得到增强，噪声则平均分布在整个单位圆上。

图4　仿真信号极坐标角频分布图Fig.4 Polar diagram angle frequency distribution of simulation signal

3应用实例

3.1变速器信号采集

实验装置如图5所示，其示意图如图6所示，采用电动机模拟发动机驱动变速器，用变速器驱动发电机模拟负载，通过基于PXI的数据采集模块采集转速信号和振动信号。变速器型号为BJ2020S，其传动示意图如图7所示。将8路601A01型振动加速度传感器布置在各轴承座径向壳体上易于安装的位置，如图8所示；转速传感器安装在输入轴上。故障设置为在变速器二档从动齿轮某齿上用电火花加工长宽深为3 mm×1.5 mm×0.15 mm的坑点模拟早期微弱点蚀故障，齿轮故障部位如图9所示。变速器置二档，调节负载励磁电压为200 V来模拟负载工况，输入轴转速为1 440 r/min，分别采集齿轮正常和早期微弱点蚀故障时的振动信号。采样频率为10 kHz，采样点数为16 384点。

图5　变速器试验装置Fig.5 Gearbox experimental setup

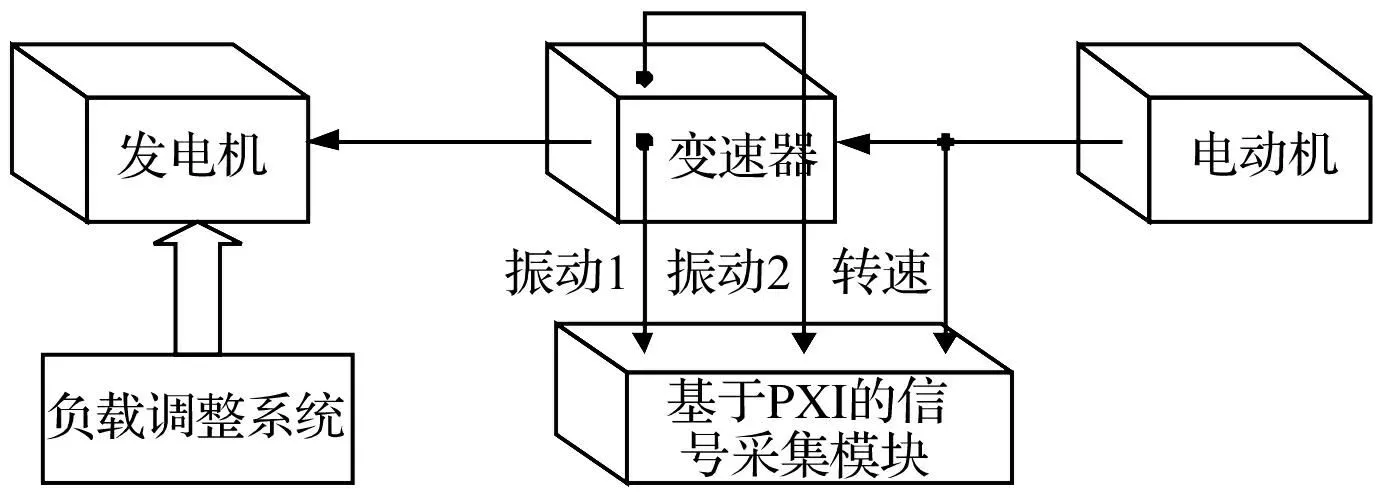
图6　变速器试验装置示意图Fig.6 Sketch map of gearbox experimental setup

图7　BJ2020S变速器传动示意图Fig.7 Drive sketch map of BJ2020S gearbox

图8　振动传感器分布Fig.8 Distribution of vibration sensors

变速器二档从动齿轮的啮合频率为

f=nz/(60i)

(7)

式中：n为输入轴转速，z为齿轮齿数，i为传动比。

二档从动齿轮齿数为28，传动比为2.33，输入轴转速为1 440 r/min，代入式(7)可得f=288 Hz，二档齿轮转频及点蚀故障调制频率为fm=10.3 Hz。

图9　齿轮故障部位Fig.9 Fault part of gear

3.2齿轮故障特征提取

图10(a)、(b)分别为二档齿轮正常与点蚀故障时的变速器壳体振动信号时域波形，从图中无法判断齿轮的故障状态。对振动信号进行连续小波变换，得到直角坐标系下的时频图(见图11)。从图11中可以看出：变速器壳体振动的能量主要集中在[600,1 400]Hz频带内；相比正常齿轮，点蚀故障的时频图中可观察到瞬态冲击成分，但由于故障冲击能量比较微弱，其周期无法辨识，这说明在噪声影响下，直角坐标系下的小波时频图对齿轮早期微弱点蚀故障分析效果不理想。

图10　振动信号时域波形Fig.10 Time domain waveform of vibration signal

图11　直角坐标系下信号时频分布图Fig.11 Time-frequency distribution in rectangular coordinate

为了增强振动信号的周期性瞬态冲击特性，将直角坐标系下的时频分布映射到极坐标系下，得到极坐标角频分布图，具体步骤为：

(1) 根据二档齿轮转频计算其每转周期T=1/fm=0.097 s及每周期采样点数970，以同时采集的某转速脉冲信号为起始点，提取出齿轮正常与点蚀工况下连续10转的振动信号。实验中为了减小转速波动的影响，选用了转速保持恒定时采集的振动信号，这时齿轮每转周期和每周期采样点数保持不变。在轴有转速波动或变转速情况下，需要首先对时域振动信号进行等角度重采样，使齿轮每转周期内重采样信号点数相等，才能提取出齿轮连续10转的振动信号。

(2) 采用Morlet小波基函数，按照式(4)对每转信号进行连续小波变换，得到时频分布系数Cx(f,Ti),i=1,2,3…10。

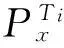
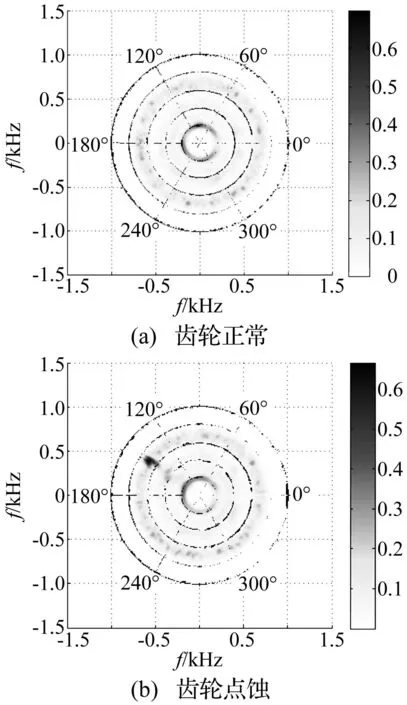
图12　振动信号极坐标角频分布图Fig.12 Polar diagram angle frequency distribution of vibration signal

按照上述步骤，得到正常与点蚀工况极坐标角频分布，如图12。从图12(a)可以看出，在齿轮正常时，由于振动信号中不存在周期性瞬态冲击成分，极坐标角频图中没有明显的增强区域。由图12(b)看出，齿轮点蚀故障时，在极坐标[150°,1 kHz]附近存在一个特征系数较大的区域，说明故障齿轮运转时，相对于每转起始时刻，故障齿转过150°时啮合产生较大的冲击能量(起始时刻不同，故障齿转过的角度也不相同)，点蚀故障引起的冲击特征能量集中在1 kHz频率左右。图12(b)与图12(a)相对比可知，齿轮正常时能量分布比较均匀，当存在点蚀故障时，冲击特征在极坐标角频分布图中得到加强，出现了能量集中(特征系数较大)区域，这是由于齿轮每个运转周期内在点蚀缺陷位置处发生能量较大的碰撞冲击。对比图11 (b)可以看出，极坐标角频图能够简洁直观地将齿轮点蚀故障凸显出来。

作为对比，将同一组点蚀故障信号进行了包络解调分析。由于变速器壳体振动的能量主要集中在[600,1 400]Hz频带内，因此对信号进行[600,1 400]Hz的带通滤波预处理，信号的包络谱如图13。图中干扰成分较多，仅在故障调制频率fm及其4倍频处有明显的峰值，2、3倍频处峰值不明显，需要仔细观察才能判断二档齿轮存在故障。说明在噪声影响下，包络法不能有效提取齿轮早期微弱点蚀故障特征。

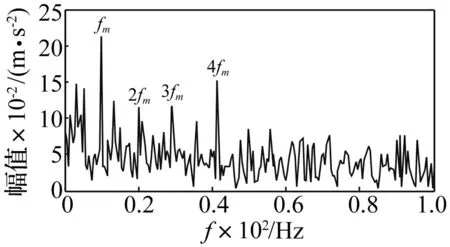
图13　故障信号包络谱Fig.13 The envelope spectrum of fault signal

4结论

(1) 齿轮早期点蚀故障冲击能量比较微弱，在噪声影响下，直角坐标系下的小波时频图无法辨识瞬态冲击的周期性，分析效果不理想。

(2) 基于增强小波时频的极坐标角频分布方法能够增强信号中周期性瞬态冲击成分，抑制非周期性的噪声干扰，与传统包络方法对比，能有效提取齿轮早期微弱点蚀故障特征。

参 考 文 献

[1] 何田，林意洲，郜普刚，等.局部均值分解在齿轮故障诊断中的应用研究[J]．振动与冲击，2011，30(6)：196-201.

HE Tian, LIN Yi-zhou, GAO Pu-gang, et al. Application of local mean decomposition in gear fault diagnosis[J]. Journal of Vibration and Shock,2011,30(6): 196-201.

[2] 李学军，蒋玲莉，杨大炼，等.基于双谱分布区域的齿轮聚类分析与故障诊断[J]．振动工程学报，2011，24(3)：304-308.

LI Xue-jun, JIANG Ling-li, YANG Da-lian,et al. Cluster analysis and fault diagnosis for gear based on bispectrum distribution[J]. Journal of Vibration Engineering,2011,24(3): 304-308.

[3] 程军圣，杨怡，杨宇.基于LMD的谱峭度方法在齿轮故障诊断中的应用[J]．振动与冲击，2012，31(18)：20-23.

CHENG Jun-sheng, YANG Yi, YANG Yu. Application of spectral kurtosis approach based on local mean decomposition(LMD) in gear fault diagnosis[J]. Journal of Vibration and Shock,2012,31(18): 20-23.

[4] 刘小峰，柏林.角域AR谱技术在齿轮故障诊断中的应用[J]．振动工程学报，2010，23(1)：113-118.

LIU Xiao-feng, BO Lin. Application of angle domain-AR spectrum technology in gearbox fault diagnosis[J]. Journal of Vibration Engineering,2010,23(1): 113-118.

[5] 梅检民，肖云魁，杨万成，等.基于分数阶傅里叶变换的邻近阶比分离研究[J]．振动与冲击，2012，31(11)：38-41.

MEI Jian-min, XIAO Yun-kui, YANG Wan-cheng, et al. Adjacent order components separation based on fractional fourier transformation[J]. Journal of Vibration and Shock，2012，31(11)：38-41.

[6] 孙海亮，訾艳阳，何正嘉.多小波自适应分块阈值降噪及其在轧机齿轮故障诊断中的应用[J]．振动工程学报，2013，26(1)：127-134.

SUN Hai-liang, ZI Yan-yang, HE Zheng-jia. Multiwavelet denoising with adaptive block thresholding and its application in gearbox diagnosis of rolling mills[J]. Journal of Vibration Engineering,2013,26(1): 127-134.

[7] 贾继德，张玲玲，曾锐利，等.变速箱齿轮磨损故障的极坐标角-频表示与诊断[J]．农业工程学报，2012，28(22)：58-62.

JIA Ji-de, ZHANG Ling-ling, ZENG Rui-li, et al. Polar diagram angle-frequency representation and diagnosis for gear wear fault of gearbox[J]. Transactions of the Chinese Society of Agricultural Engineering,2012,28(22): 58-62.

第一作者 杨青乐 男，硕士生，1999年生

摘要：针对变速器齿轮早期故障中周期性瞬态冲击不显著的问题，在小波变换的基础上提出了极坐标增强的方法。该方法利用齿轮运行的旋转特性，将直角坐标下多个运转周期的小波时频分布，转化为角度-频率分布并映射到极坐标平面。诊断实例表明，该方法能够抑制非周期性的噪声干扰，增强了振动信号的周期性瞬态冲击特征，有效诊断出齿轮早期微弱点蚀故障。

关键词：齿轮；早期点蚀；极坐标；增强

Fault diagnosis for gear early pitting based on polar coordinate enhancement

YANGQing-le,ZHANGLing-ling,JIAJi-de,MEIJian-min,GENGShuai(Department of Military Automobile, Military Transportation University, Tianjin, 300161)

Abstract:The periodic transient impact effect of gear early fault is weak as usual. In order to settle this problem, the method of polar coordinate enhancement based on Continuous Wavelet Transform was proposed. Considering the rotation feature of a running gear, time frequency distributions of the signal in several cycles obtained in rectangular coordinate were transformed to angular frequency distributions and then mapped into a polar coordinate plane. The experimental results show that the nonperiodic noise is restrained, while the periodic transient impact feature of signal is enhanced, and the gear early pitting fault can be diagnosed more effectively.

Key words:gear; early pitting; polar coordinate; enhancement

中图分类号:TH165+.3

文献标志码：A DOI:10.13465/j.cnki.jvs.2015.24.002

通信作者贾继德 男，教授，硕士生导师，1962年生

收稿日期：2014-07-25修改稿收到日期：2014-12-05

基金项目：总装备部预研课题项目(ZLY2011601)