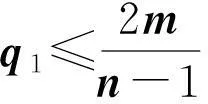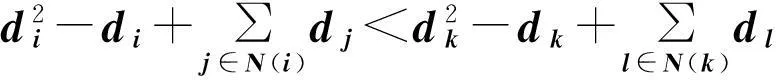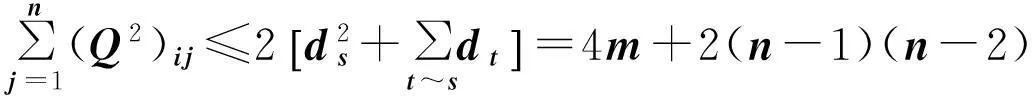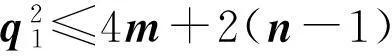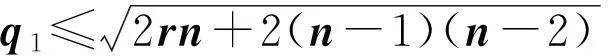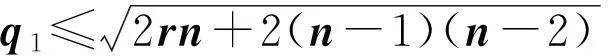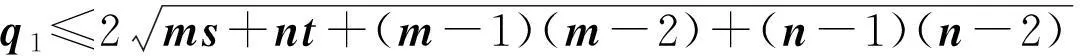循环图的无符号拉普拉斯谱半径

周后卿

(邵阳学院 理学与信息科学系，湖南 邵阳 422000)



循环图的无符号拉普拉斯谱半径

周后卿

(邵阳学院 理学与信息科学系，湖南 邵阳 422000)

摘要：给出一个图G，称矩阵Q=D+A为无符号拉普拉斯谱矩阵，其中A表示G的邻接矩阵，D表示G的顶点度对角矩阵.研究了循环图的无符号拉普拉斯谱半径的上界，得到了几个有意义结果.进一步，讨论了循环图的卡氏积图的无符号拉普拉斯谱半径上界。

关键词:循环图;无符号拉普拉斯矩阵;谱半径

图谱理论的一个思想就是利用大量的图和矩阵之间的关系，即与图形有关的矩阵的特征值来研究图的一些问题.因为有很多图矩阵可用于此目的，譬如，图的邻接矩阵，图的拉普拉斯矩阵.对于图的邻接矩阵，拉普拉斯矩阵研究较多，有许多文献.而研究图的无符号拉普拉斯矩阵的文献相对少一些[1-4].为此，我们在本文中着重讨论循环图的无符号拉普拉斯谱半径问题.设G=(V，E)是一个具有顶点集V={v1，v2，…，vn} 的简单连通图.假设顶点vi的度为di，不妨设d1≥d2≥…≥dn，记G的度对角矩阵为D(G)，邻接矩阵为A(G)(以下简称D与A).假设A的特征值为λ1，λ2，…，λn，并且设λ1≥λ2≥…≥λn.把Q=A+D称作图G的无符号拉普拉斯矩阵，因为无符号拉普拉斯谱相比图的其他矩阵 (拉普拉斯矩阵，Seidel矩阵)，它似乎更方便用于图的性质研究，因而受到部分学者的重视与研究.让R表示图G的关联矩阵，则有RRT=A+D，RTR=AL+2I，这里，AL表示G的线图L(G)的邻接矩阵，I表示n阶单位矩阵.因为矩阵RRT和RTR的非零特征值相同，所以线图L(G)与Q之间有如下关系 PL(G)(λ)=(λ+2)m-nQG(λ+2)，PL(G)(λ)表示矩阵AL的特征多项式；QG(λ)表示矩阵Q的特征多项式，也叫图G的Q多项式；m，n分别图G的边数与顶点数.这个关系揭示了线图与无符号拉普拉斯矩阵的特征值之间的直接联系。

1矩阵Q的谱半径的一些结果

称图G为循环图，若它的邻接矩阵是一个循环矩阵，即它是循环群上的Cayley图.循环图是一类重要的互联网络拓扑图，一些网状互联网络实质上就是循环图对应的网络.循环网络是双环网的自然推广.循环图具有许多优良性质，它具有较好的稳定性，高对称性，可扩展性，它是点可迁的.在过去20多年里，循环图不断出现在编码理论，VLSI设计，Ramsey理论，并行计算和分布式计算中。

定义G与H的Cartesian积G×H:其顶点集为V(G×H)=V(G)×V(H)，其中任何两个顶点 (u，u′)，(v，v′)相邻当且仅当u=v且u′，v′在H中相邻;或u′=v′且u，v在G中相邻，这里u，v∈V(G)，u′，v′∈V(H)。

给出嵌套分裂图的定义[5]:称G为嵌套分裂图，若G的顶点可以排序，只要i≤j且p≤q，则由 jq∈E(G)就可以推出ip∈E(G)。

嵌套分裂图可以是一个连通图，也可以是一个连通图与一些孤立点的并。

图G具有Q特征值q1，q2，…，qn，并且q1≥q2≥…≥qn，称最大特征值q1为G的Q谱半径或G的Q指标.鉴于无符号拉普拉斯矩阵Q是半正定矩阵，它的特征值都是非负的.对于Q谱半径，下列命题成立：

设G是一个具有Q谱半径q1的图.则

(1)q1=0 当且仅当G是一个空图；

(2) 0

(3)对于连通图有q1=4当且仅当G的分支是一个圈图或星图K1，3。

文献[1]证明了连通图的无符号拉普拉斯矩阵Q的最小特征值为0当且仅当该图是一个二部图;并且还证明了任何图的Q特征值为0的重数等于二部图的分支数。

确定图的Q谱半径问题是图谱理论的一个重要问题[6，7]，有一部分学者对与无符号拉普拉斯相关的问题进行了研究，得到了一些深刻的结果[8-11].文献[2]证明了下列结果:设G是一个具有顶点度为d1，d2，…，dn的图，它的最大Q特征值为q1.则

文献[4]同样给出了q1的一个上界：设G是一个具有n个顶点m条边的连通图。

2引理与结论

为了证明本文的定理，我们需要下列引理。

引理1[3]设G是一个固定顶点和边数，且具有最大Q特征值q1的图，则G不可能包含下列任何一个导出子图：2K2，P4，C4。

现在证明下列引理：

引理2设G是一个具有n个顶点m条边的图.则G的最大Q特征值q1满足

Q2=(D+A)2=D2+DA+AD+A2，

（4）当施氮量达到101.46 kg·hm-2时，理论上可达到最高产量，田面水中总氮浓度相对较低，氮素流失风险较低，是兼顾经济效益与环境效益的较好方案，但尚需要通过后期长期试验进一步验证。

接下来证明本文主要结论：

定理4设G是一个具有n个顶点度为r的循环图.则G的最大Q特征值q1满足

证明由G是一个具有n个顶点度为r的循环图，因此，有rn=2m.从而根据引理2，有

定理5设G，H分别是具有m，n个顶点，度为s，t的两个循环图.则G，H的卡氏积图G×H的最大Q特征值q1，有

参考文献：

[6]Zhang X D.The signless Laplacian spectral radius of graphs with given degree Sequence[J].Discrete Applied Mathematics，2009，157:2928-2937。

[7]Liu M，Tan X，Liu B.The (signless) Laplacian spectral radius of unicyclic and bicyclic graphs with n vertices and k pendant vertices[J].Czechoslovak Mathematical Journal，2010，135：849-867。

[8]Abreu N，Cardoso D.M，Gutman I.Bounds for the signless Laplacian energy[J].Linear Algebra and its Applications，2011，435： 2365-2374。

[9]Ayyaswamy S K，Balachandran S，Venkatakrishnan Y B.Signless Laplacian Estrada index[J].MATCH Commun.Math.Comput.Chem，2011，66:785-794。

[10]Binthiya R，Sarasija P B.On the signless Laplacian energy and signless Laplacian Estrada index of extremal graphs[J].Applied Mathematical Sciences， 2014，8：193-198。

[11]Feng L H，Yu G H.On three conjectures involving the signless Laplacian spectral radius of graphs[J].Publ.Inst.Math.(Beograd)，2009，85(99)：35-38。

[12]Cvetkovic D，Doob M，Sachs H.Spectra of Graphs: Theory and Application[M].New York:Academic Press，1980.

Signless Laplacian Spectral Radius for Circulant Graphs

ZHOU Hou-qing

(DepartmentofScienceandInformationScience，ShaoyangUniversity，Shaoyang，Hunan422000，China)

Abstract:Given a graph G，the matrix Q=D+A is called the signless Laplacian，where A is the adjacency matrix and D is the diagonal matrix of vertex degrees.We survey upper bounds of spectral radius of signless Laplacians for circulant graphs.Moreover，we derive upper bounds of the Cartesian product graph。

Key words:circulant graph;signless Laplacian matrix; spectral radius

作者简介：周后卿(1963—)，湖南新邵人，硕士，教授，研究方向：组合数学及应用.E-mail:zhouhq2004@163.com

基金项目：湖南省教育厅科学研究项目(15C1235);邵阳市科技局科技计划项目(2015JH41)

收稿日期：2015-06-01

中图分类号：O157.5

文献标志码：A

文章编号：1672-7010(2015)04-0003-04