环Fq+uFq+u2Fq+…+uk-1Fq上线性码的覆盖半径

钟家伟,　李　平

(合肥工业大学 数学学院,安徽 合肥　230009)



环Fq+uFq+u2Fq+…+uk-1Fq上线性码的覆盖半径

钟家伟,李平

(合肥工业大学 数学学院,安徽 合肥230009)

摘要:文章研究了有限链环R=Fq+uFq+u2Fq+…+uk-1Fq上长为n的线性码关于齐次距离的覆盖半径,其中uk=0,q为某一素数幂。构造了环R上的广义Gray映射,得到了R上线性码关于覆盖半径的相关性质,并研究了环R上线性码覆盖半径的上下界。

关键词:线性码;齐次距离;齐次重量;Gray映射;覆盖半径

0引言

有限链环上的齐次重量是有限域上的Hamming重量和剩余类环Z4上Lee重量的推广,对有限链环上码的结构和相关度量的研究有着重要意义。文献[1]最先将齐次重量的概念引入编码理论研究中;文献[2]研究了有限环上齐次重量的存在性与唯一性,得到了有限环上齐次重量的一种计算公式；文献[3]利用生成特征标研究了Frobenius环上齐次重量的另一种计算公式；文献[4]在文献[2]的基础上得到Galois环上的齐次重量的表达形式,并构造出有限环上的代数几何码,同时还研究了环上齐次重量的上下界。

近年来,有限链环R=Fq[u]/(uk)引起编码爱好者极大的兴趣。有限链环上线性码的齐次重量对揭示有限链环上线性码的结构和相关性质有着非常重要的作用。同时,有限链环上线性码的齐次重量对构造有限链环上的最优码也起着重要作用。目前,已有许多文献研究了环上线性码的齐次重量的相关性质，如文献[5-8]。文献[9]研究了Z4上Lee距离和欧几里德距离的覆盖半径；文献[10]研究了环F2+uF2上Lee距离的覆盖半径;文献[11]研究了Zpm上Lee距离的覆盖半径。 本文在文献[10-11]的基础上构造了环R上的保距广义Gray映射,由此得到R上关于齐次距离覆盖半径的上下界及其相关性质。

1R上的广义Gray映射

设Fq为某一个q元域,取Fq中的向量v=(1,1,1,…，1),w=(0,1,2,…，q-1)。令

(1)

即

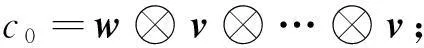
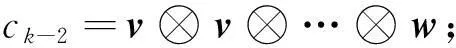
其中，k∈N*；δi,j表示Kronecker符号；i=0,1,…,k-1；⊗表示Fq上的张量积运算。

由文献[12]可知(u)为R的唯一极大理想,对于R中任意元素x可唯一表示为:

其中，xi∈Fq。

定义1对于R上任意元素x=x0+ux1+u2x2+…+uk-1xk-1,若存在φ使得:

环R上长为n的线性码是Rn的R-子模。设C为Fq上长为n的线性码,wh(x)表示C上的码字x=(x0,x1，…，xn-1)的Hamming重量。dh表示线性码C上的Hamming距离,则易知dh为线性C上非零码字的极小Hamming重量,即

定义2设C为环R上的线性码,w(C)表示C的齐次重量,显然w(C)是R上的重量函数,即对于任意的r∈R,w:R→N,且

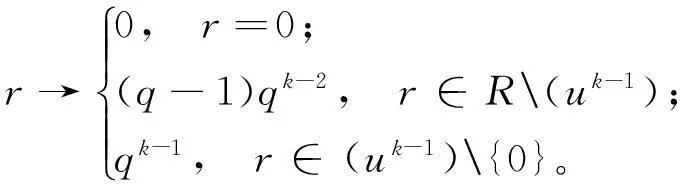
对任意的x=(x0,x1…xn-1)∈C,其齐次重量为:

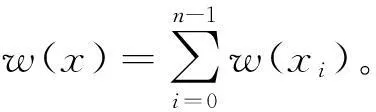
对于线性码C,其齐次距离d(C)为[8]:

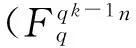
证明对任意的r=r0+ur1+…+uk-1rk-1∈R,则有：

(1) 当r=0时,φ(0)=(0,0,0,…,0),显然

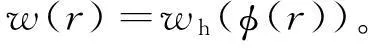
(2) 当r∈(uk-1){0}时,有

由定义2可知w(r)=wh(φ(r))。

(3) 当r∈R(uk-1),令

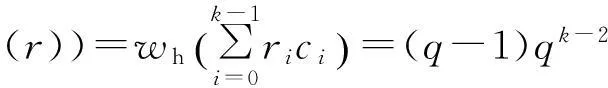
综上可得,设x=(x0,x1,…,xn-1)为R上长为n的码字,则

证毕。

引理2设C为Fq上长为n的线性码,φ(C)是C的广义Gray映射,则

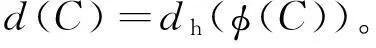
证明对于任意的x∈C,由引理1可知x≠0当且仅当φ(x)≠0,x∈C,当且仅当φ(x)∈φ(C),因此d(x)满足:

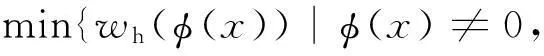
证毕。

2码的覆盖半径

给出环R上线性码关于齐次距离覆盖半径的概念,研究R上线性码关于齐次距离覆盖半径上下界的相关性质。

定义3设C为环R上的线性码,r表示C上齐次距离的覆盖半径,

由上述定义可知,对于任意u∈Rn,令

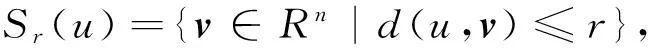
定理1设r(C)为环R上的线性码C关于齐次距离的覆盖半径,则有r(C)=rh(φ(C))成立,其中rh(φ(C))是定义在Fq上关于Hamming距离的覆盖半径。

证明由r(C)的定义以及引理2可得:

r(C)=max{d(u,C)|∀u∈Rn}=

max{dh(φ(u),φ(C))|∀u∈Rn}=

rh(φ(C))。

证毕。

为了更进一步得到R上线性码覆盖半径的性质,研究其上下界的情况。

定理2假设C是环R上长为n的线性码,则有：

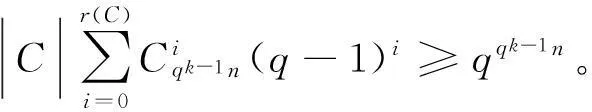
由引理1知φ为保距同构映射,因此有|φ(C)|=|C|成立,定理得证。

定义4设C是环R上长为n的线性码,则对任意的x∈Rn,x+c={x+c|∀c∈C}称作x关于加法子群C的陪集,每个陪集中的最小重量称做该陪集的重量,记为wh(x+c)[10]。

在研究中,发现陪集首对于研究线性码覆盖半径起着非常重要的作用。

定理3设C是环R上长为n的线性码,则C上的线性码关于齐次距离的覆盖半径r(C)等于C的全体陪集的陪集首齐次重量的最大值。

证明当x跑遍Rn时,-x也跑遍Rn,于是

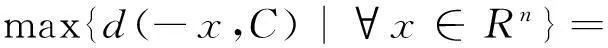
证毕。

由于R上线性码有着良好的性质,显然R上线性码的直和以及直积也是R上的线性码。构造R上线性码直和、直积以及线性组合的码,对其上覆盖半径进行了相关的研究。

定义5设C1、C2是R上长为n的线性码,记C1与C2的直和为:

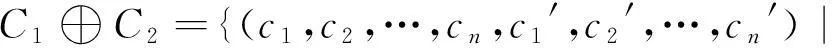
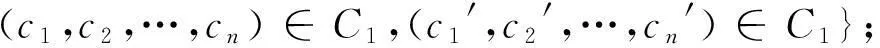
C1与C2的直积为:

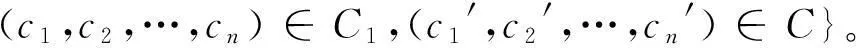
引理3设C1、C2是R上长为n的线性码[13],则

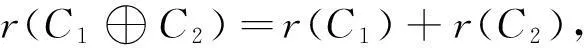
r(C1*C2)≥max{n1r(C1),n2r(C2)}。

引理4令C1、C2为R上长为n的线性码, G1、G2分别为C1、C2的生成矩阵,若线性码C的生成矩阵为[14]：

则r(C)≥r(C1)+r(C2)。其中，A为R上的矩阵。

引理3、引理4可由文献[13-14]直接得到,在此不再证明。以上结论还可以推广至R上有限个线性码的直和、直积以及线性组合码覆盖半径的性质,结果依然成立。

设C1、C2也是R上的线性码,C1⊂C2，则可得到C1覆盖半径的一个下界。

定理4设C1、C2是R上的线性码,C2的极小重量记为d(C2)。若C1⊂C2,则有:

证明令ν是C2C1中极小重量的码字,则ν是C1的陪集首,故w(ν)≥d(C2),所以

证毕。

定义C的对偶码C⊥为:

其中，x·y是x与y的直积。若C⊆C⊥,则称C自正交,若C=C⊥则称C是自对偶。

引理5令ν是C的陪集首,若μ是ν的子集,且μ、ν为非零码字，则μ也是C的陪集首[14]。

在定理5中得到了R上线性码的对偶码的覆盖半径的一个上界。

定理5对于环R上线性码C,记

则有：

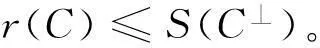
其中，Ai(C⊥)表示C⊥中齐次重量为i的码字的数目。

证明令C是[n,k,d]线性码,D是由C以及C的陪集C+{ν}所生成的(n,k+1)码,其中ν是陪集首。由于C⊂D，则D⊥⊂C⊥,因此D⊥最多有S(C⊥)个不同的齐次重量,由于码字来自C或者C+{aν},其中a≠0,a∈R,aν在DC中有极小齐次重量。因此给出了C的齐次重量分布,当DC中所有码字的极小齐次重量至少为S(C⊥)时,D⊥的齐次重量分布就唯一决定了。由Macwilliams恒等式可知,当w(ν)≥S(C⊥)时,D的齐次重量分布是唯一决定的。由定理3可知,一个陪集首能达到的最大齐次重量是S(C⊥),因此r(C)≤S(C⊥)。证毕。

3结束语

本文构造环上的广义Gray映射,推广了文献[10-11]的结果。研究环R上的线性码关于齐次距离的覆盖半径与域Fq上的线性码关于汉明距离的覆盖半径之间的关系,得到了R上覆盖半径上下界。进一步,还研究了R上线性码的直和、直积以及线性组合码的覆盖半径。最后,得到了R上自对偶码的覆盖半径上下界的相关性质。

[参考文献]

[1]Constantinescu I, Heise W. A metric for codes over residue class rings of integers [J].Problemy Peredachi Infromatsii, 1997,33(3):22-28.

[2]Greferath M, Schmidt S E. Finite-ring combinatorics and Macwilliams’ equivalence theorem [J]. J Combin Theory, Ser A, 2000(92):17-28.

[3]Honold T. Characterization of finite Frobenius ring [J].Arch Math (Basel),2001,76(6):406-415.

[4]Voloch J F,Walker J L.Homogeneous weights and exponential sums [J].Finite Fields Appl,2003,9(3):310-321.

[5]Byrne E, Greferath M, Honold T. Ring geometries, two-weight codes, and strongly regular graphs [J]. Des Codes, Crypt, 2008(48):1-16.

[6]Greferath M, O’Sullivan M E. On bounds for codes over Frobenius rings under homogeneous weights [J]. Discrete Mathematics, 2004, 289:11-24.

[7]Greferath M, McGuire G, O’Sullivan M E.On plotlin-optimal codes over finite Frobenius ring [J]. Journal of Algebra and Its Applications, 2006(5):799-815.

[8]Greferath M,Schmidts S E. Gray isometries for finite chain rings and a nonlinear ternary (36,312,15)ode [J]. IEEE Trans Inform Theory, 1999, 45(7):2522-2524.

[9]Aoki T, Gaborit T, Harada M, Ozeki M and Sole P. On the covering radius of Z4codes and their lattices[J]. IEEE Trans Inform Theory, 1999,45(6):2162-2168.

[10]李平,朱士信,余海峰.环F2+uF2上码的覆盖半径[J].中国科学技术大学学报,2008,38(2):145-148.

[11]Manish. K. Gupta C. Durairajan. On the covering radius of some modular codes[J]. eprint arXiv: 1206-3038.

[12]Heise W, Honold T,Nechaev A. Weighted modules and representations of codes[J]. Probl Peredachi Inf，1999,35(3):18-39.

[13]Assmus E F,Pless V. On the covering radius of extremal self-dual codes[J]. IEEE Trans Inform Theory, 1983(29): 359-363.

[14]Cohen G D, Karpovsky M G, Mattson H F,et al.Covering radius-Survey and recent results[J]. IEEE Trans Inform Theory, 1985(31): 328-343.

(责任编辑马国锋)

李平(1971-),男,安徽无为人,博士,合肥工业大学副教授,硕士生导师.

Covering radius of linear codes over ringFq+uFq+u2Fq+…+uk-1Fq

ZHONG Jia-wei,LI Ping

(School of Mathematics, Hefei University of Technology, Hefei 230009, China)

Abstract:In this paper, the covering radius of linear codes over R=Fspan+uFspan+u2Fspan+…+uspanFspanwith length n about homogeneous distance is studied, where uspan=0, q is a power of prime. Some properties of linear codes over R about homogeneous distance are obtained by generalized Gray map. The upper and lower bounds of covering radius of linear codes over R about homogeneous distance are also studied.

Key words:linear code; homogeneous distance; homogeneous weight; Gray map; covering radius

中图分类号:TN911.22

文献标识码：A

文章编号：1003-5060(2015)03-0424-04

doi:10.3969/j.issn.1003-5060.2015.03.027

作者简介：钟家伟(1990-),男,安徽六安人,合肥工业大学硕士生;

基金项目：国家自然科学基金资助项目(61370089);中央高校基本科研业务费专项资金资助项目(J2014HGXJ0073)和合肥工业大学博士学位人员专项基金资助项目(JZ2014HGBZ0029)

收稿日期：2014-01-15；修回日期：2014-04-10