基于测量值均匀量化的扩展卡尔曼滤波

朱朝阳，文成林，叶海红

(杭州电子科技大学系统科学与控制工程研究所，浙江 杭州 310018)



基于测量值均匀量化的扩展卡尔曼滤波

朱朝阳，文成林，叶海红

(杭州电子科技大学系统科学与控制工程研究所，浙江 杭州 310018)

摘要：介绍了传输信道中传感器节点能量和带宽有限的问题，并进一步提出了带宽受限情况下首先进行量化处理的特点。指出状态非线性量测为线性的模型采用量化处理的扩展卡尔曼滤波与同样条件下未采用量化处理的扩展卡尔曼滤波相比，从量化误差、量化份数两方面对滤波器的性能进行研究，此方法能在带宽小情况下，具有量化误差同样小的优点，并利用计算机对一类状态非线性量测线性模型的仿真结果有效性进行了实验分析。从而得出此类特定系统在带宽有限时，运用此量化策略同样可降低量化误差的结论。

关键词：均匀量化；带宽受限；扩展卡尔曼滤波；量化误差

0引言

卡尔曼滤波(Kalman filter，KF)主要运用于线性系统，扩展卡尔曼滤波(Extended Kalman Filter，EKF)主要运用于非线性系统[1]。国内外同期在EKF的量化上主要有对测量值、新息量化策略研究，和对数量化等非均匀量化方面的探索。无线传感器网络在传输过程中往往有带宽限制。因此，在确保量测量化误差可接受范围下，怎样降低对通信方面带宽要求是传感器网络研究的关键问题[2]。本文在带宽受限情况下，对信息先进行量化后再传输。采用一类模型为状态方程非线性，量测方程线性，并对同模型下是否采用量化策略误差等数据进行对比，计算机仿真结果表明，此类系统采用量化策略的EKF不仅需要带宽小，并且量化误差小。

1采用测量值均匀量化策略的EKF介绍与算法设计

1.1　系统描述

考虑传感器非线性系统，其模型可描述为：

x(k+1)=Φ(x(k)，k)+ω(k)

(1)

z(k)=Η(k)x(k)+v(k)

(2)

式中，x(k)∈Rn为目标状态值，z(k)∈Rq为传感器测量值，Φ∈Rn×1为x(k)、k的非线性函数，Η(k)∈Rq×n为测量转移矩阵，ω(k)∈Rn×1和v(k)∈Rq×1分别为过程噪声和测量噪声向量。

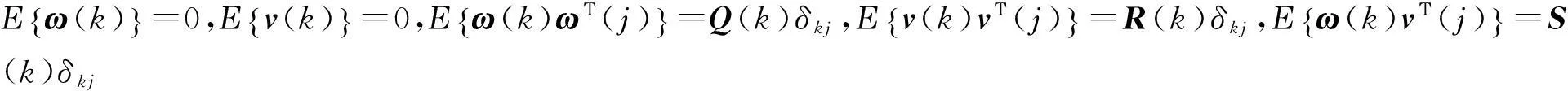
假设2初始状态x(0)统计独立于ω(k)和v(k)[3]。

1.2　测量值量化策略

在此设z(k)为标量值z(k)，测量值z(k)经量化后，形式为m(k)=z(k)+n(k)。其中，m(k)为测量值z(k)经量化后的量，n(k)为量化噪声。

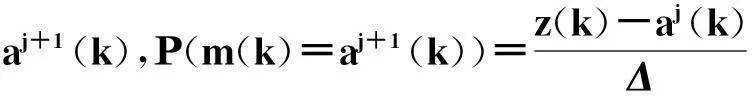
量化噪声方差为：

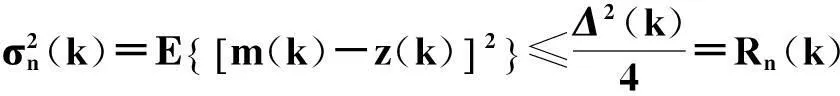
(3)

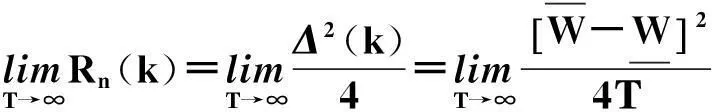
1.3　核心算法

为计算方便，本文设置一维的传感器测量值，基于1.2节中量化策略，系统方程为：

x(k+1)=Φ(x(k)，k)+ω(k)

(4)

m(k)=Η(k)x(k)+θ(k)

(5)

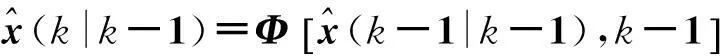
(6)

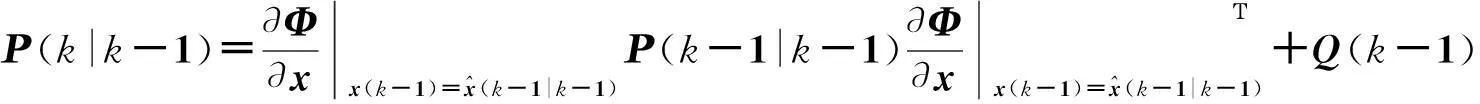
(7)

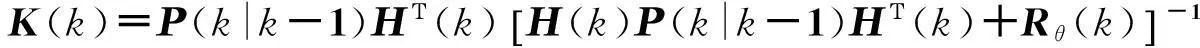
(8)

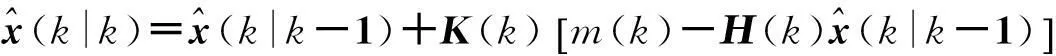
(9)

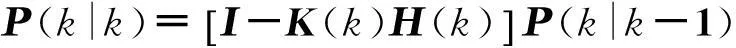
(10)

2仿真实验

2.1　实验数据准备

2.2　仿真结果

为比较采用量化策略的扩展卡尔曼滤波(Kalman Filter Based On Quantitative Measurements，KFBOQM)与未采用量化的最优扩展卡尔曼滤波(Kalman Filter Based On Original Measurements，KFBOOM)的均方误差(MSE)，仿真实验中，状态值x为固定值，取量化份数T为1，5，10，50，100，测量值z分为5组，每组取100个。在同等条件下，随着T值的变化，采用两种量化策略的扩展卡尔曼滤波的MSE变化如表1所示。

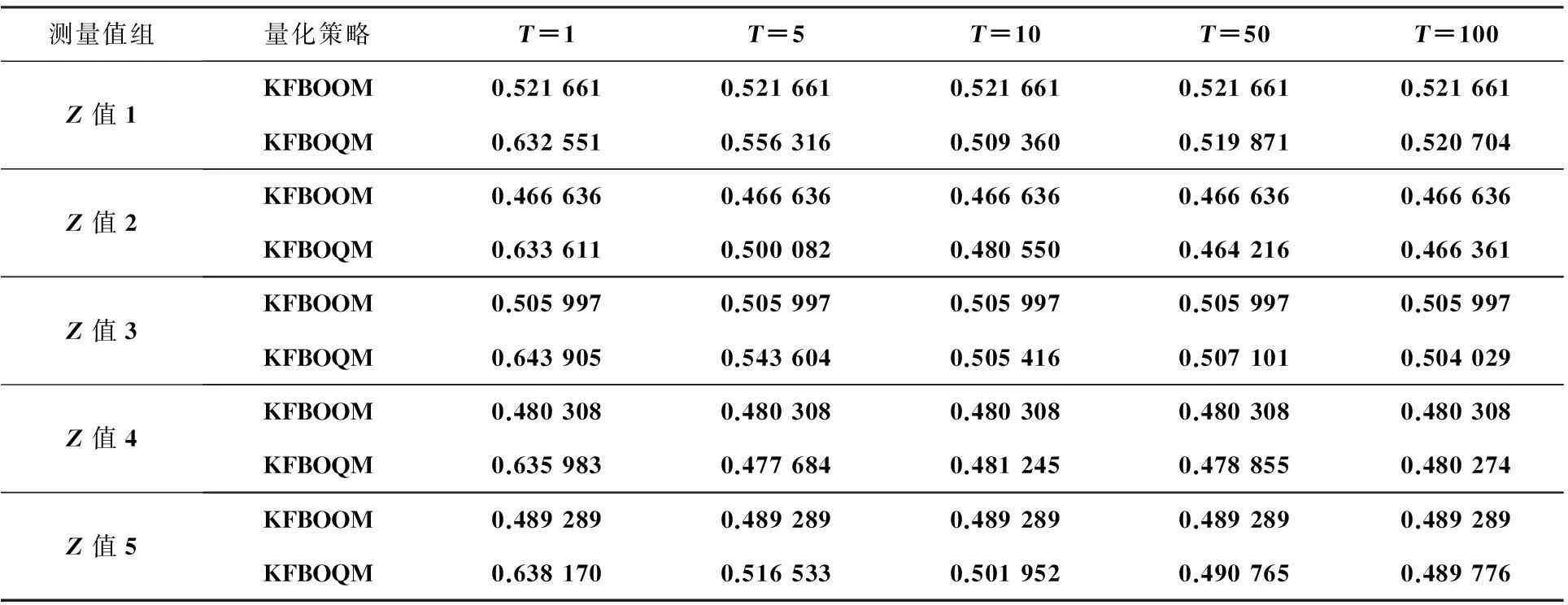
表1　KFBOOM与KFBOQM下的MSE值对比仿真结果

表1中，同样非影响因素条件下，随着量化份数的增加，KFBOQM的MSE越来越接近KFBOOM的MSE，由量化理论知当量化份数趋于无穷时，噪声方差趋于0，即此时KFBOQM与KFBOOM的MSE相等。因此表1的仿真结果验证了量化理论中的噪声方差随量化份数增大而减小。

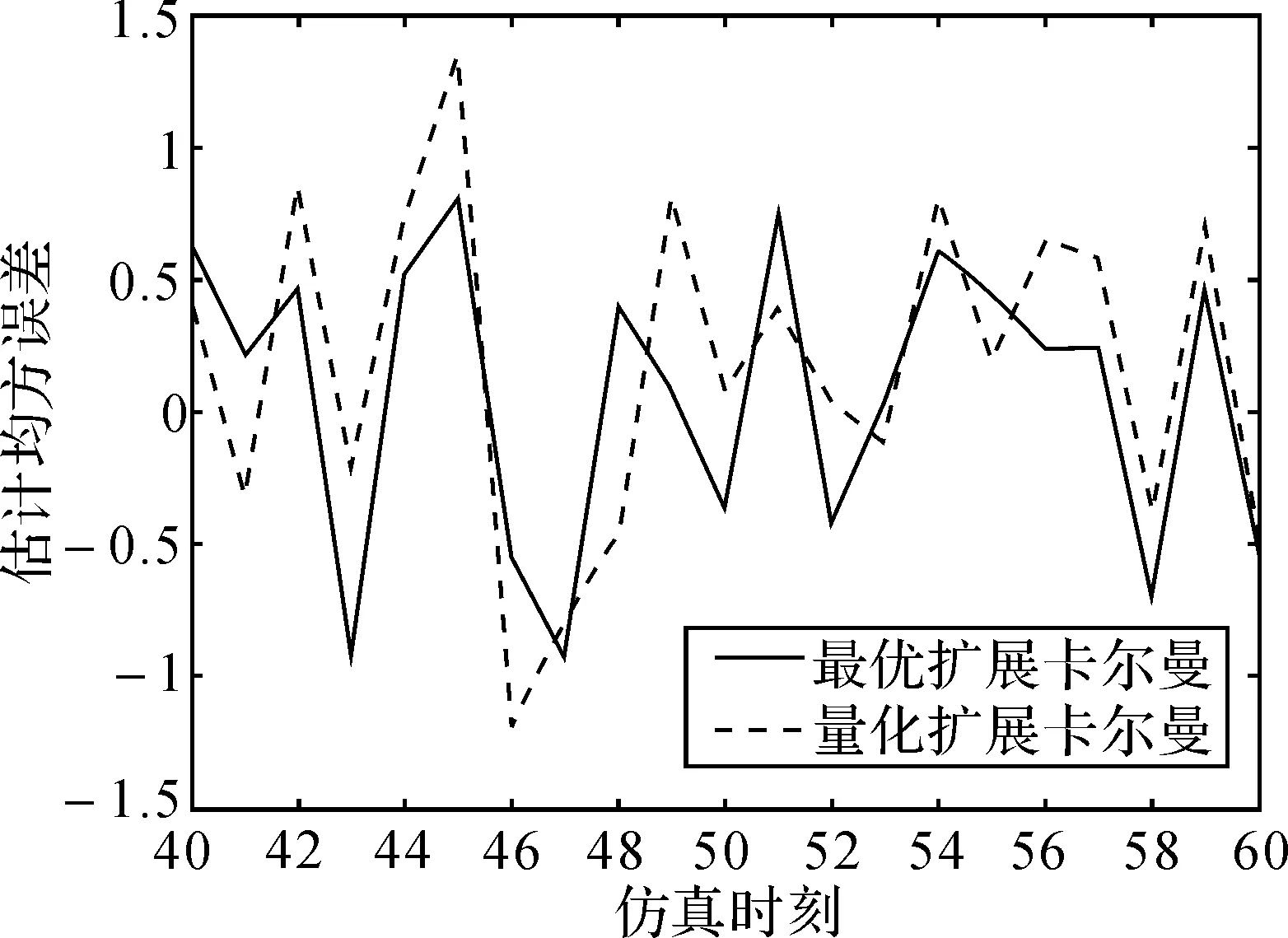
图1　T=1时两种策略均方误差对比

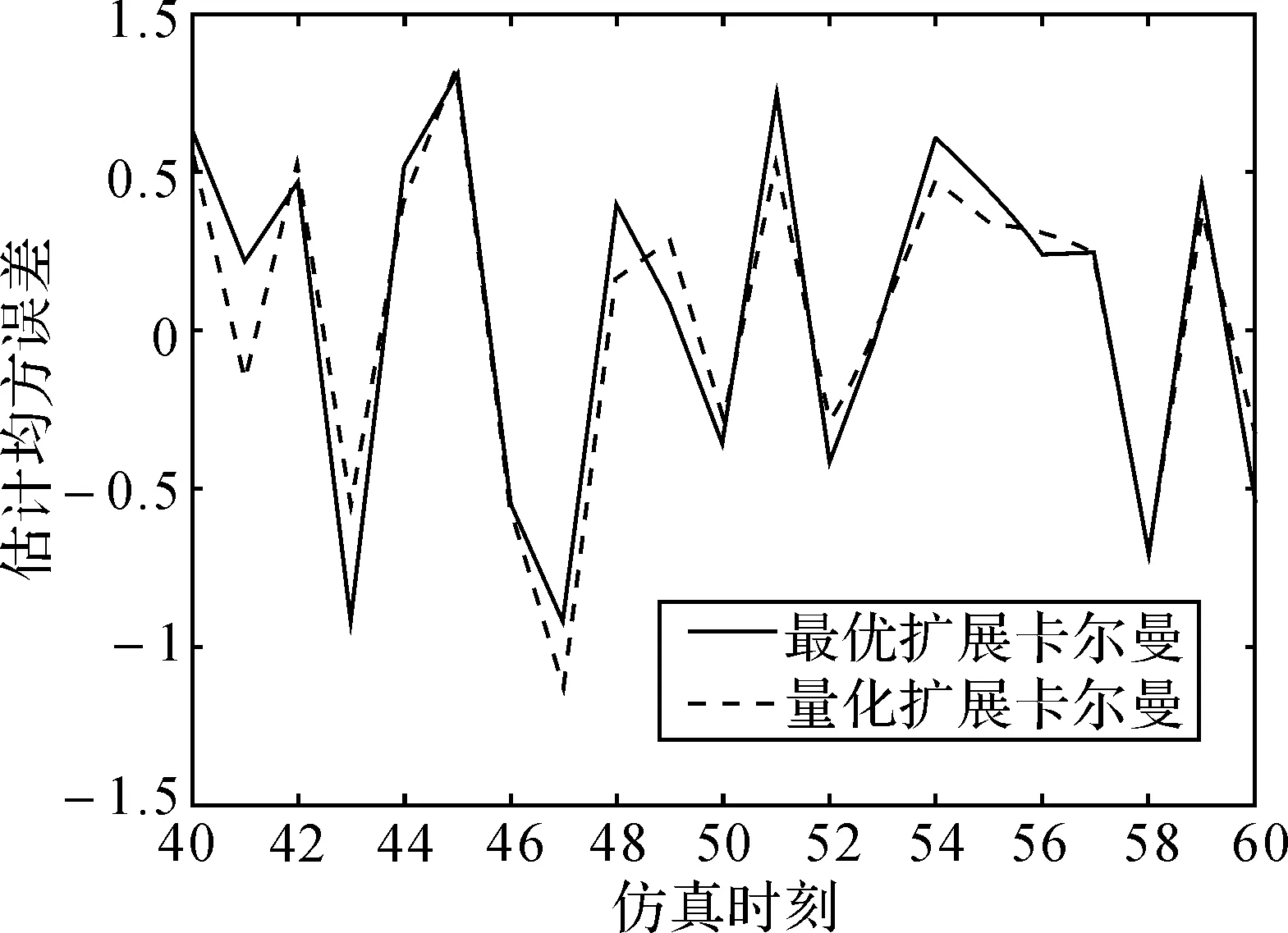
图2　T=5时两种策略均方误差对比

图3　T=10时两种策略均方误差对比

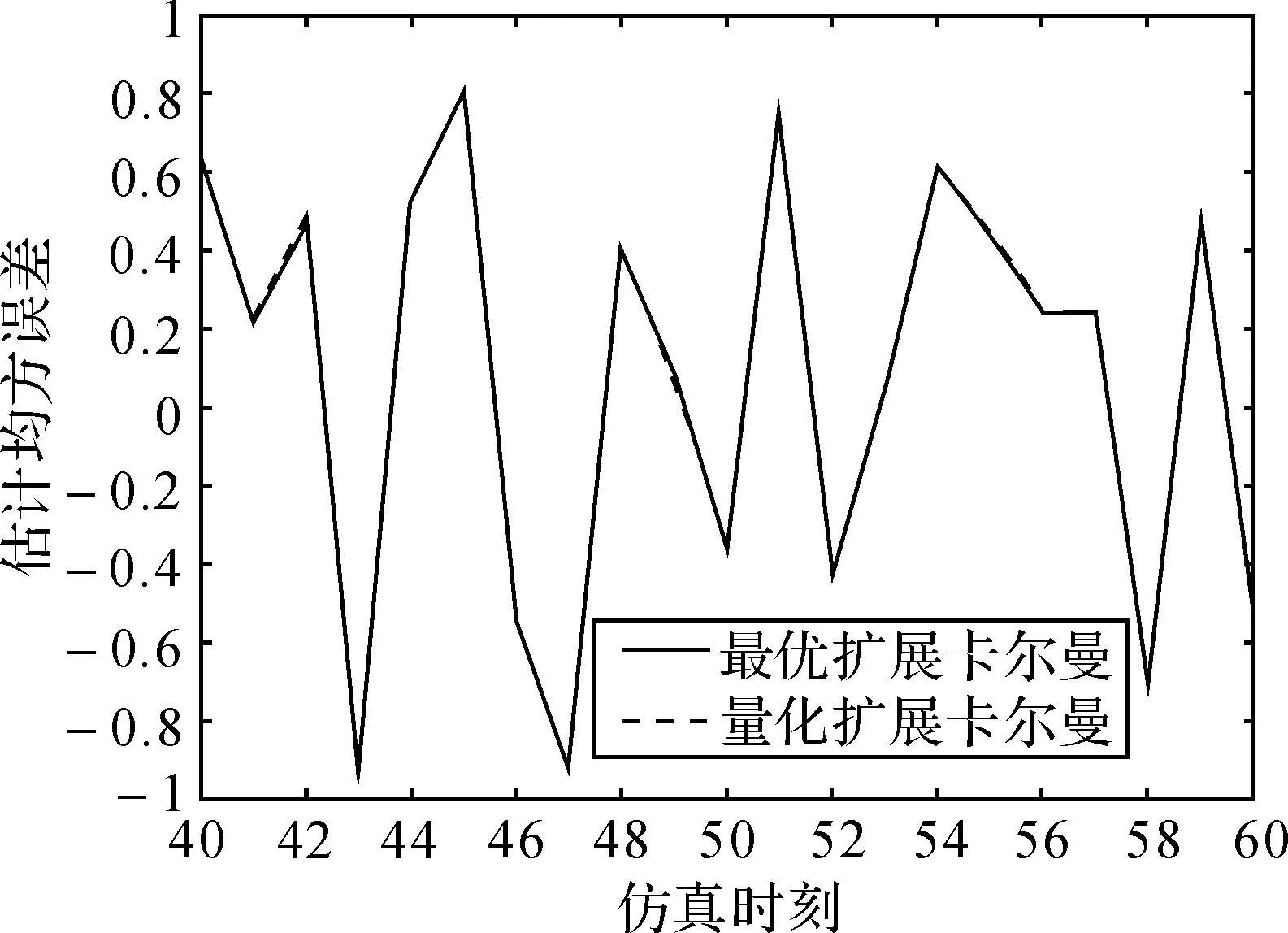
图4　T=100时两种策略均方误差对比

3结束语

EKF适用于系统状态和观测方程不都是线性情况下，在滤波误差及一步预测误差较小时效果好。但无线传感器网络中，传输信道宽不可能是无限的。此刻确保带宽约束下，信息传输不失真成为研究关键。本文的仿真结果验证了KFBOQM算法的准确有效，均方误差能在合理条件下接近KFBOOM的均方误差。且此算法计算量增加不大，在工程上有一定价值。本文主要针对一类非线性系统采用了对测量值的均匀量化策略，在有些实际模型中，非均匀量化效果更好。

参考文献

[1]于洪波，王国宏，孙芸，等.一种融合UKF和EKF的粒子滤波状态估计算法[J].系统工程与电子科学，2013，35(7):1375-1379．

[2]文金仓.基于不同量化策略的Kalman滤波器的性能分析[D].开封:河南大学，2013：1-4．

[3]文成林.多尺度动态建模理论及其应用[M].北京:科学出版社，2008：66-98．

[4]陈博.网络化多传感器信息融合估计算法研究[D].杭州:浙江工业大学，2013：1-12．

[5]葛泉波，李文斌，孙若愚，等.基于EKF的集中式融合估计研究[J].自动化学报，2013，39(6):816-825．

[6]文成林，陈志国，周东华.基于强跟踪滤波器的多传感器非线性动态系统状态与参数联合估计[J].电子学报，2002，30(11):1715-1717．

[7]汤显峰.基于传感器网络的数据融合算法研究[D].杭州:杭州电子科技大学，2009：53-68．

Research on Uniform Quantization for Measured Value of EKF

Zhu Chaoyang，Wen Chenglin，Ye Haihong

(InstituteofSystemsScienceandControlEngineering，HangzhouDianziUniversity，HangzhouZhejiang310018，China)

Abstract:This paper introduces sensor node energy and bandwidth is often limited in bandwidth constraint.Quantitative processing under bandwidth constraints are proposed and comparing whether carry out quantitative processing or not under the model which has linear state and nonlinear measurement，we can know the quantization error is small with low bandwidth by using quantitative processing in terms of quantization error and quantitative copies.It is indicated that the effectiveness of the new algorithm is also illustrated by use.Thus the use of quantitative strategy also can reduce the quantization error when such specific system is in bandwidth constraints．

Key words:uniform quantization；bandwidth constraint；extended Kalman filter；quantization error

中图分类号：TP13

文献标识码：A

文章编号：1001-9146(2015)05-0036-04

通信作者：

作者简介：朱朝阳(1990-)，男，河南禹州人，在读研究生，信息融合.文成林教授，E-mail：wencl@hdu.edu.cn．

基金项目：国家自然科学基金资助项目(61371064，61304186，61271144)

收稿日期：2014-12-16

DOI:10.13954/j.cnki.hdu.2015.05.008