基于ABAQUS/CFD的径向滑动轴承参数化数值模拟

张青雷, 唐玉良, 徐　欣

(1.上海理工大学 机械工程学院,上海　200093;

2.上海电气集团股份有限公司 中央研究院,上海　200070)



基于ABAQUS/CFD的径向滑动轴承参数化数值模拟

张青雷1,2, 唐玉良1, 徐欣2

(1.上海理工大学 机械工程学院,上海200093;

2.上海电气集团股份有限公司 中央研究院,上海200070)

摘要：针对径向滑动轴承种类多,腔内压力油流动复杂,传统的基于理论编程的方法很难获得其精确模型的问题,采用ABAQUS/CFD软件建立了某径向滑动轴承计算流体动力学参数化仿真模型,分析得到了稳态下油膜压力与油膜流速的分布规律。结果表明,该型滑动轴承稳态特性符合设计要求;参数化的模型还可延用于后续大量的计算与分析,不仅为该系列滑动轴承的设计制造及试验分析提供了仿真依据,同时也开辟了一种新的高效经济的研究方法。

关键词：径向滑动轴承; 计算流体动力学; 参数化; 数值模拟

1引言

滑动轴承是大型旋转类装备机械的核心部件,其性能的优劣很大程度地影响着设备能否安全高效地运转[1,2],因此在设计或选用滑动轴承时需要对其支承特性进行计算与评估。目前国内外学者在工程应用上仍借助有限差分等方式求解雷诺方程,通过人工编程,进而模拟滑动轴承的静动特性[3-5]。而雷诺方程是纳维-斯托克斯方程的简化,推导过程忽略了假设黏度、密度不变及油膜曲率等因素的影响[6,7];当待测轴承结构较复杂或者种类较多时,人工编程不仅难以获得精确的分析模型,而且费时费力,传递性也不够好。

计算流体动力学(Computational Fluid Dynamics,CFD)与计算机的结合,可通过数值模拟和图像显示对油膜润滑过程进行仿真分析,用一系列离散单元来模拟原本在时间和空间域上连续的物理场,通过建立这些单元上场变量的代数方程组并加以求解,最终获得整体流场的数值解。近年来Fluent、CFX、FIDIP等流体分析软件应运而生,已在工程应用方面取得了良好效果。蔡林[8]基于计算流体动力学软件Fluent,分析了流体动压滑动轴承静特性,给出了供油压力、供油温度和空穴压力对静特性的影响规律。孟凡明[9]等人探讨了CFX和Fluent软件在径向滑动轴承润滑计算结果的异同。Deligant[10]等人建立了发动机涡轮增压器径向滑动轴承三维流体分析模型,得到了其摩擦功率损耗值。但采用上述软件进行流体分析时也存在着一定的不足:网格划分需要其它软件预处理,数据传输存在失真,无法实现参数化建模。

ABAQUS/CFD采用间断Galerkin有限体积/有限元法来计算不可压缩流体的层流和湍流问题,该方法为二阶精度计算方法,比目前常用流体分析软件所采用的一阶精度计算方法更先进,并且可在一个统一的界面下完成流体分析的前、后处理,便于实现参数化建模,并行运算效率也非常高。

本文基于ABAQUS/CFD软件,建立了某型径向滑动轴承参数化三维模型,实现了边界条件参数化设置和六面体网格自动划分,计算得到了稳态下的油膜压力及油膜流速的分布规律,为该型滑动轴承的设计及试验提供了仿真依据,该方法也可有效地应用于后续更多滑动轴承的研发与试验过程。

2控制方程

流体运动遵循的物理定律主要包括质量守恒定律(连续性方程)、动量守恒定律(运动方程)和能量守恒定律。本文所涉及的宏观流体力学范围内的流体运动,可由以下控制方程加以描述。

2.1质量守恒定律

单位时间内,从外界流入某流体微元的质量与流出该微元的质量之差等于该流体微元质量的增量,即:

(1)

当流体为不可压缩且定常流动流体时,上式(1)可写成:

(2)

2.2动量守恒定律

流体微元的动量对时间的变化率等于流体微元所受外部作用力之和,即:

(3)

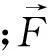
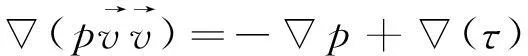
(4)

(5)

式中:μ为黏性系数;I为单位张量。

2.3能量守恒定律

流体微元中输入与输出的能量之差等于总能量的增量,即

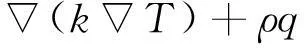
(6)

式中:e为流体微元储能;v为流速;为梯度算子;k为传热系数;T为温度;q=-λT表示轴瓦固体内部导热方程,λ为导热系数。

3模型的建立

3.1三维模型

以图1所示的某型径向滑动轴承为研究对象,轴承的结构示意图如图2所示,具体尺寸如下:转子轴颈d=150 mm,轴承宽度b=90 mm,进油口宽度lin=18 mm,出油口宽度lout=15 mm,半径间隙c=0.04 mm。润滑油从上部进油口进入楔形油腔,在转子旋转带动其运动过程中,润滑油先流经出油口,再从两端面泄出。根据轴承结构尺寸,本文在ABAQUS前处理环境中建立了滑动轴承油膜的参数化三维仿真模型,如图3所示,可通过修改参数方便地改变轴承油膜的结构与尺寸,自动生成相应的三维模型。

图1　某型径向滑动轴承Fig.1　Radial sliding bearing

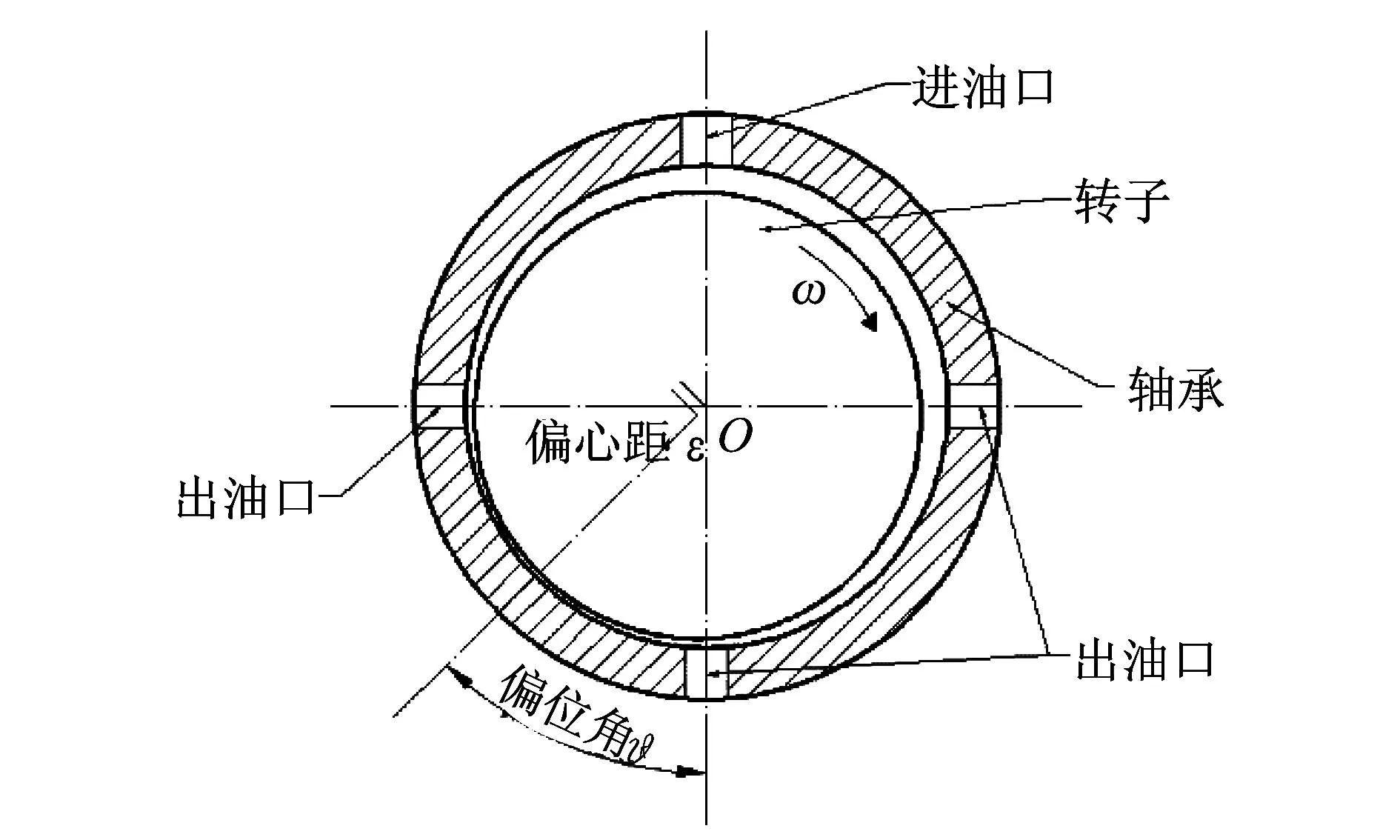
图2　滑动轴承结构示意图Fig.2　Structure of sliding bearing

3.2基本假设与边界条件

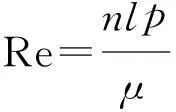
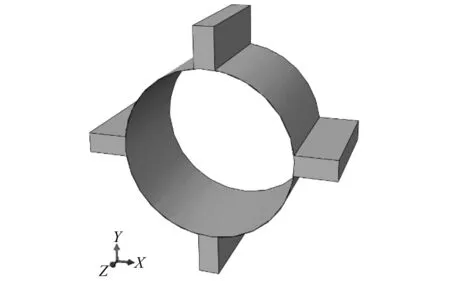
图3　油膜三维模型Fig.3　Three-dimensional model of oil film

边界条件设置如下:润滑油密度ρ=860 kg/m3,润滑油动力黏度μ=0.0277 Pa·s,供油压力取pin=0.14 MPa,室温20 ℃,出油背压与大气压相等pout=0.101 MPa,转子旋转速度为1 000 r/min,其余均为壁面边界,转速为零。

3.3网格划分

滑动轴承油膜厚度尺寸远小于轴承直径和轴承宽度尺寸,但厚度方向却是计算的关键,必须划分足够多的网格层数以保证壁面速度梯度不影响整体流场结果,因此整体油膜网格数必将达到很大的数目,并且可能会形成狭长的网格单元,容易引起计算不收敛,所以需要进行六面体网格划分。本文基于Python语言,在ABAQUS/CFD环境中编辑了六面体网格参数化划分程序,可以轻松地获得油膜六面体网格模型,如图4(a)所示,(b)为(a)的局部放大图。由图4可知,整个油膜模型由均匀的六面体网格单元组成,在油膜厚度方向上更是划分了20层六面体网格,满足了计算需求。

理论上,网格数越多,计算精度越高,但计算耗时相应也越长,对计算机性能的要求也越高。为了寻找到一个合适的网格密度,分析网格独立性,以便今后对该类模型进行大规模运算,形成数据库,本文以模型中某一固定位置的油膜压力为计算指标,通过修改网格参数,对八组不同网格密度模型进行计算,得到了网格独立性曲线,如图5所示。由图5可知,随着网格数的增多,油膜压力值有所下降,但幅度越来越小,到80万网格时已满足前后误差为1%的设计精度;相反,计算耗时却由5 min延长至大约45 min。综合考虑以上因素,本文最终选取网格总数约为80万的计算模型。

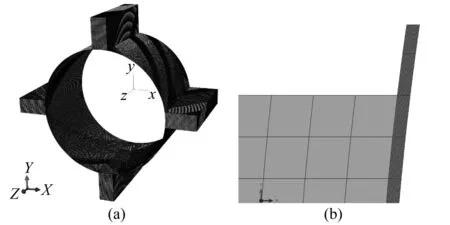
图4　油膜网格划分Fig.4　Grid division of oil film

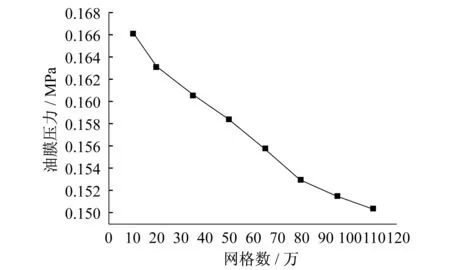
图5　网格独立性曲线Fig.5　Grid independence curve

4结果与分析

生成径向滑动轴承油膜的三维模型,设置了边界条件并完成六面体网格划分的过程,也即相应地在ABAQUS/CAE中形成了前处理操作的日志文件。通过参数化日志文件中的结构尺寸及添加所需的关键字,就可以形成滑动轴承参数化计算流体动力学仿真程序,再将其提交计算便可得到油膜压力及油膜流速等分布规律。如图6所示即为其中部分仿真程序,在ABAQUS/CAE中运行该程序脚本,即可生成对应的.inp文件,用于提交运算。

图6　参数化仿真程序Fig.6　Parametric simulation program

需要指出的是,ABAQUS/CFD不仅可以在ABAQUS/CAE这样一个统一的环境中进行模型的前、后处理,而且可以同时进行热-固-流等多物理场耦合分析。本文所建立的某径向滑动轴承油膜压力参数化仿真分析模型,可为后续多种尺寸径向滑动轴承的支承特性数值模拟打下基础,只需修改对应参数并添加相应的边界条件即可。

本文通过设置进、出油压力与流速边界,调整膜厚方向网格层数,进行了多组模型的计算比较,结合实际滑动轴承试验分析经验,得到数值模拟计算结果如下所示。

图7为稳态下,滑动轴承油膜压力分布等值线图。可知最大油膜压力为0.1529 MPa,位置出现在轴承下方靠近最薄油膜厚度附近,这是由于转子带动油膜顺时针旋转并伴有一定偏位造成的。由于起承载作用的主要是轴承下半圆,因此下半周油膜平均压力大于上半周油膜平均压力,差值用以克服转子重力。以油膜压力最大位置为界,向两边逐渐减小,最小油膜压力位置出现在轴承顶部进油口附近,并且出现了局部的负压。三个较大的出油口由于和外界大气相连,其附近压力值和大气压接近。这种油膜压力分布规律可为该型滑动轴承物理试验过程中压力传感器的选型与布置提供仿真依据。

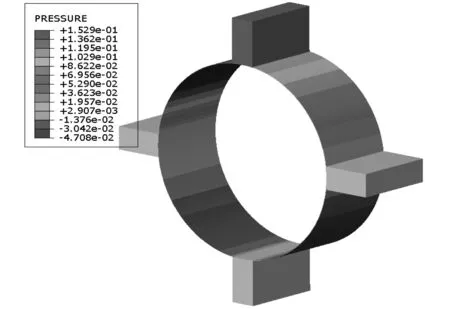
图7　油膜压力分布Fig.7　Pressure distribution of oil film

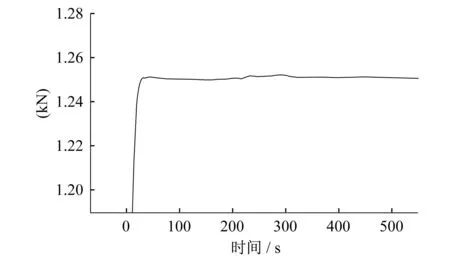
图8　油膜支承合力曲线Fig.8　Support force curve of oil film

读取油膜内圈与转子接触的圆环面的面力即油膜支承合力,如图8所示。可以发现,在所设置的1000个载荷步中的第80步左右,油膜力就已经达到稳定状态,合力大小约为1250 N,方向向上,表明该型滑动轴承静态支承稳定性较好。

图9(a)为油膜流速分布等值线图,(b)为(a)的局部放大图,便于观察油膜厚度方向的流速梯度。本文设油膜外侧为壁面,转速为零,内侧随转子无滑移地转动,因此最大流速为7850 mm/s,流速由内而外逐级递减。结合图9(b)局部放大图可以发现,在出油口位置,流体流速大小也是由内而外逐级递减,并在出油口一侧平稳地流出润滑油,出口拐角位置未出现大的扰动,表明滑动轴承的润滑油出口形状及其尺寸的设计比较合理。

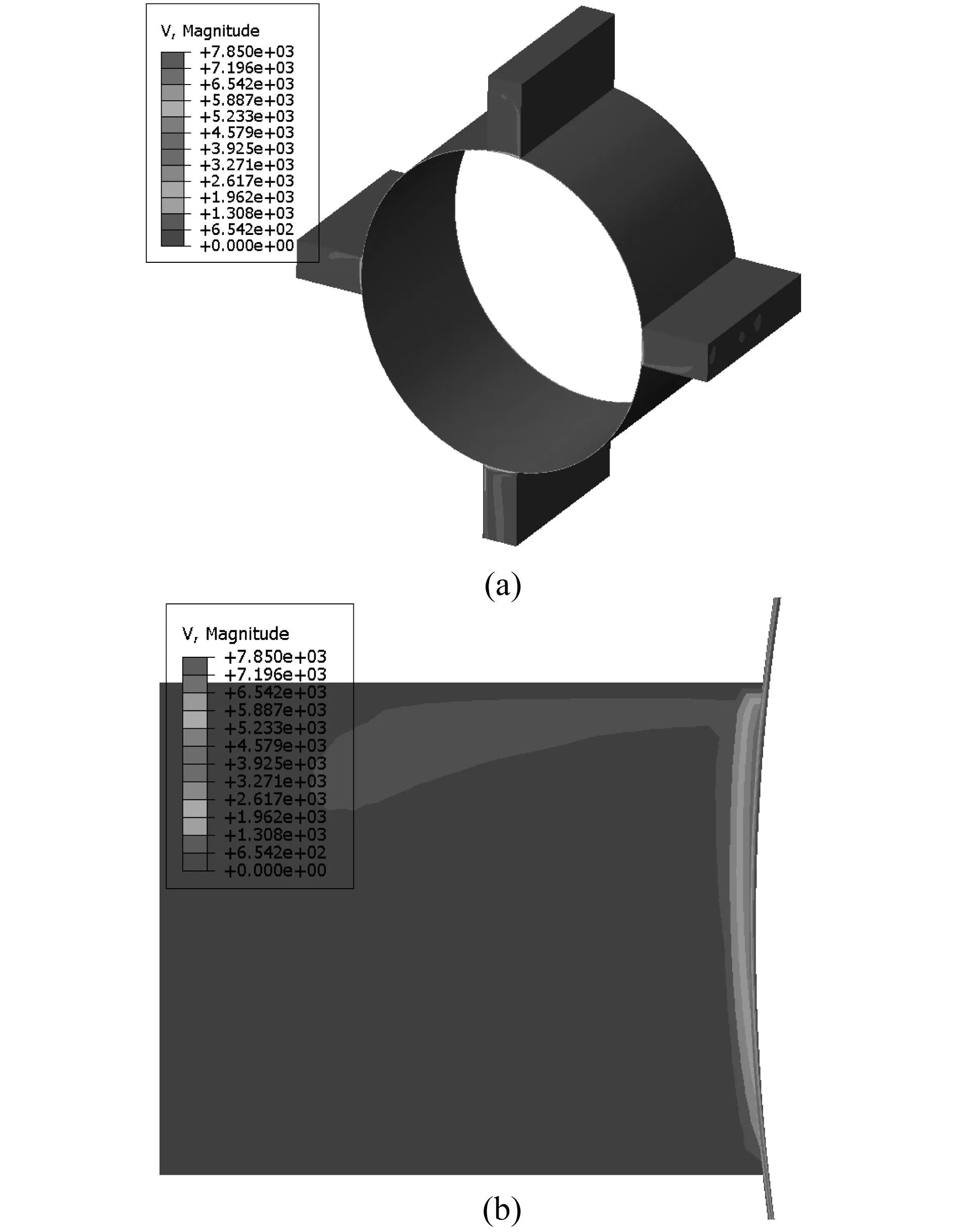
图9　油膜流速分布Fig.9　Flow velocity distribution of oil film

5结论

基于ABAQUS/CFD软件建立了径向滑动轴承计算流体动力学参数化仿真模型,完成了六面体网格自动划分及网格独立性分析,实现了边界条件参数化设置,分析得到了稳态下油膜压力与油膜流速的分布规律,形成了一套参数化的滑动轴承仿真分析方法。该方法运算效率高,分析得到的计算趋势可为滑动轴承的设计、制造及试验提供仿真依据与参考,可有效地缩短新型滑动轴承的研制周期,大大降低物理试验的次数及成本。

参考文献:

[1]曹春建,张德虎,辛华荣,等.螺旋油楔动静压滑动轴承三维CFD仿真分析[J].机械设计与制造,2013,(8):70-73.

CAO Chunjian,ZHANG Dehu,XIN Huarong.Three-Dimensional CFD Numerical Analysis of Spiral Oil Wedge Hybrid Journal Bearing[J].Machinery Design and Manufacture,2013,(8):70-73.

[2]黎伟.多瓦可倾瓦径向滑动轴承热润滑性能的研究[D].杭州:浙江大学,2013.

LI Wei.Thermal lubrication study of multi tilting-pad journal bearing[D].Hangzhou:Zhejiang University,2013.

[3]尹伟,段京华,孙军等.滑动轴承润滑分析中的边界条件[J].轴承,2013,12:56-60.

YIN Wei,DUANJinghua,SUN Jun.Boundary Conditions in Lubrication Analysis of Journal Bearings[J].Bearing,2013,12:56-60.

[4]V.Meruane,R.Pascual.Identification of Nonlinear Dynamic Coefficients in Plain Journal Bearings [J].Tribology International,2008,41:743-754.

[5]T Stolarski.Numerical Modeling and Experimental Verification of Compressible Squeeze Flim Pressure [J].Tribology International,2010,43:356-360.

[6]高庆水,杨建刚.基于CFD方法的液体动压滑动轴承动特性研究[J].润滑与密封,2008,33(9):65-67.

GAO Qingshui,YANG Jiangang.Research on the Dynamic Characteristics of Hydro dynamical Journal Bearing Based on CFD Analysis[J].Lubrication Engineering,2008,33(9):65-67.

[7]马涛,戴惠良,刘思仁.基于Fluent的液体动静压轴承数值模拟[J].东华大学学报,2010,36(3):279-282.

MA Tao,DAI Huiliang,LIU Siren.Numerical Simulation Study on Liquid Hybrid Bearing Based on FLUENT[J].Journal of Donghua University,2010,36(3):279-282.

[8]蔡林.流体动压滑动轴承静特性研究[D].哈尔滨:哈尔滨工程大学,2012.

CAI Lin.Investigation on Static Performance of Hydrodynamics Bearing[D].Harbin:Harbin Engineering University,2012.

[9]孟凡明,陈原培,杨涛.CFX和Fluent在径向滑动轴承润滑计算中的异同探讨[J].重庆大学学报,2013,36(1):7-14.

MENG Fanming,CHEN Yuanpei,YANG Tao.Discussion on similarities and differences between CFX and Fluent software in calculating journal bearing lubrication[J].Journal of Chongqing University,2013,36(1):7-14.

[10]M Deligant,P Podevin,G Descombes.CFD Model for Turbocharger Journal Bearing Performances [J].Applied Thermal Engineering,2011,31:811-819.

张青雷男(1973-),上海人,教授级高级工程师,博士,主要研究方向为数字化设计与制造。

唐玉良男(1989-),河南信阳人,硕士,主要研究方向为有限元分析和应用。

Parametric Simulation of Radial Sliding Bearing Based on ABAQUS/CFDZHANGQinglei1,2,TANGYuliang1,XUXin2

(1.College of Mechanical Engineering,University of Shanghai for Science and Technology,shanghai 200093,China;

2.Shanghai Electric Group Co .,Ltd.Central Academy,shanghai 200070,China)

Abstract：In view of the variety of radial sliding bearing,the complex flow of pressure oil in the cavity,and the traditional theory based programming method is difficult to obtain the accurate model of the problem,using ABAQUS/CFD software to establish a radial sliding bearing calculation of fluid dynamics simulation model,analysis of the steady state oil film pressure and oil film flow velocity distribution law.The results show that the steady-state characteristics of the sliding bearing are in accordance with the design requirements.The model can be used for the subsequent large number of calculation and analysis,not only for the design and manufacture of the sliding bearing of the series,but also provides a new research method of high efficiency.

Key words：radial sliding bearing;computational fluid dynamics;parameterization; numerical simulation

基金项目：上海市2013年度服务业发展引导资金资助项目(cn2013000016)

中图分类号：TP 391.9

文献标识码：A