基于稀疏图表示的特征选择方法研究*
2016-01-26王晓栋,严菲,谢勇等
基于稀疏图表示的特征选择方法研究*
通信地址:361024 福建省厦门市集美区厦门理工学院计算机与信息工程学院Address:College of Computer and Information Engineering,Xiamen University of Technology,Xiamen 361024,Fujian,P.R.China
王晓栋,严菲,谢勇,江慧琴
(厦门理工学院计算机与信息工程学院,福建 厦门 361024)
摘要:特征选择旨在降低待处理数据的维度,剔除冗余特征,是机器学习领域的关键问题之一。现有的半监督特征选择方法一般借助图模型提取数据集的聚类结构,但其所提取的聚类结构缺乏清晰的边界,影响了特征选择的效果。为此,提出一种基于稀疏图表示的半监督特征选择方法,构建了聚类结构和特征选择的联合学习模型,采用l1范数约束图模型以得到清晰的聚类结构,并引入l2,1范数以避免噪声的干扰并提高特征选择的准确度。为了验证本方法的有效性,选择了目前流行的几种特征方法进行对比分析,实验结果表明了本方法的有效性。
关键词:特征选择;半监督学习; l2,1范数;l1范数
1引言
进入21世纪以来,社交网络、数字多媒体的爆发式发展,给人们的日常生活带来了便利的同时也提供了前所未有的机遇。然而,随之而产生的大量高维、复杂的数据,也给现有的多媒体应用系统带来了挑战,如图像内容检索、图像理解等[1,2]。处理这些高维的数据不但需要消耗大量的计算时间和存储空间,而且高维数据间往往存在较多的冗余特征,如果这些特征得不到处理,将影响到多媒体应用系统的鲁棒性和准确性,因此有必要对这些高维数据进行降维处理。
特征选择方法旨在选择数据集中最具代表性的特征,进而降低数据源的维度,是近年来的研究热点[2~5]。根据所处理的数据集是否具有类别标签,特征选择方法一般可以分为监督、无监督和半监督的特征选择方法。在监督特征选择方法中[3],首先利用已知数据集及其类别标签训练学习模型,然后根据所计算出的模型将待处理数据集进行特征选择。由于已知类别标签中包含较多可区分(Discriminative)信息,因此监督特征选择方法能够取得较好的识别效果。然而,获取大量的类别标签需要消耗大量的人力成本,且当已知类别标签数据较少时,该类方法将会失效。无监督特征选择方法假设待处理数据集服从某种分布,如流形结构,进而自动提取数据的类别标签,无需提前获取训练数据的类别标签。最大方差MaxVar(Maximum Variance)[4]为最简单的无监督特征选择方法,它根据数据方差来评价特征的重要性并进行特征筛选。LS(Laplacian Score)[5]对最大方差进行了扩展,在其基础上引入了对数据空间局部结构的分析。但是,MaxVar和LS都仅考虑到了特征本身的特点,而忽略了各个特征之间的相关性,从而导致其缺乏鲁棒性且易陷入局部最优。为了解决特征之间的相关性问题,许多学者提出借助图模型提取数据的底层流形结构,并在多种应用场景下取得了较好的效果。谱聚类是基于图模型的典型方法,例如,MCFS(Multi-Cluster Feature Selection)[6]采用谱聚类和l1范数获取数据的稀疏子空间。与MCFS思想相似,MRFS(Minimize the feature Redundancy for spectral Feature Selection)[7]在采用谱聚类的同时引入了l2,1范数,使其所获得的数据子空间不但具有稀疏特性,还能有效地消除离群点的干扰。NDFS(Nonnegative Discriminative Feature Selection)[8]利用K阶最近邻方法来描述特征类别间的相关性,并与线性分类器相结合,在对特征进行降维的同时可得到特征分类的类别标签。无监督特征选择方法克服了监督方法人力成本高的问题,但由于缺少人工类别标签导致其可区分性不高,影响了该类方法的特征选择效果。因此,为了克服监督方法人力成本高、无监督方法可区分性不高的问题,研究者们提出了半监督的特征选择方法,是监督方法和无监督方法的一种折衷。在LS的基础上,文献[9]提出一种半监督的特征选择方法,和LS一样采用逐个筛选特征的方式,但忽略了特征之间的相关性。文献[10]提出一种基于Trace Ratio的半监督特征选择方法TRCFS(Trace Ratio Criterion for Feature Selection),该方法建立在图模型的基础上,但其对噪声不敏感,且同样忽略了特征之间的相关性。SFSS(Structural Feature Selection with Sparsity)[11]提出一种基于谱聚类的半监督特征选择方法,由于该方法在模型求解过程往往需要将离散解松弛化为连续解,模糊化了各个分类之间分界线,从而影响到特征选择的效果。
为了解决以上问题,本文利用l1-范数和l2,1-范数构建了聚类结构和特征选择的联合学习模型,提出一种基于稀疏图的半监督特征选择方法SSFS(Semi-supvervised Spectral Feature Selection withl1-norm graph)。相对于现有特征选择方法,该方法具有如下几个优点:
(1)采用聚类结构和特征选择联合学习模型,在对多媒体数据进行特征选择的同时,并能得到数据的类别标签;
(2)引入l2,1范数过滤冗余特征,克服现有的特征选择模型中l2-范数约束模型容易受到孤立点(Outlier)的干扰的缺点,有效地避免了数据集中噪声的干扰;
(3)引入l1-范数约束图模型,能够得到更为清晰的聚类结构,提高特征选择的准确度。
2相关方法介绍
2.1 l1-范数和l2,1-范数
在统计学领域中,l1-范数常常被用于稀疏表达,在通信领域中也称为压缩感知,给定任意向量v∈Rn,l1-范数可以表示为:
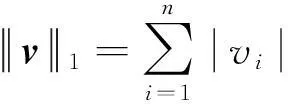
(1)
矩阵的l2,1范数[12,13]是在特征选择领域最新被提出的一种范数,取任意矩阵M∈Rr×p,其l2,1范数的表示形式如下所示:
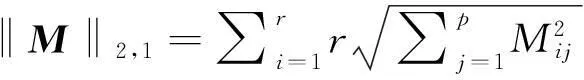
(2)
从公式(2)可以看出,l2,1范数能够对矩阵M的整行进行约束,确保矩阵M能够按行稀疏,因此,该范数有利于排除噪声的干扰,非常适合于特征选择的相关应用场景。
2.2 谱聚类
给定一个具有c个分类和n组数据的数据集X={x1,x2,…,xn},其中xi∈Rd(1≤i≤n)是第i组数据,设Y={y1,y2,…,yn}T∈Rn×c,其中yi∈{0,1}c×1为数据集X的类别标签。谱聚类的目的是将数据集X分为c类,使得属于同一类别的数据之间距离最小,而类之间的数据间的距离最大。
传统的谱聚类算法为在数据集上构建一个加权图,进而将数据的分类转化为图分割问题。设G={X,A}为数据集X所构建的加权图,X为图G的顶点,A∈Rn×n为相似矩阵,用于描述各顶点之间的相似关系,如Aij描述了顶点xi与xj的相似度。相似矩阵的构造可以采用ε近邻图、K-近邻图、全连通图[14]等方法。本文采用K-近邻图,其模型表示为:
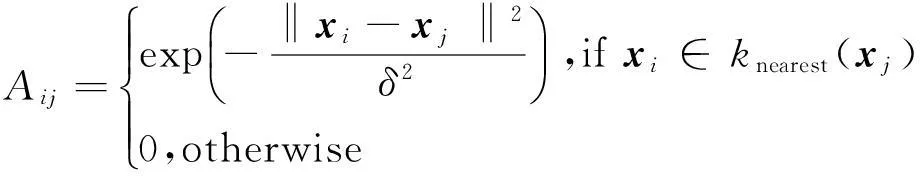
(3)
其中,knearest(·)是K-近邻函数,xi∈knearest(xj)表示xi属于xj的K-近邻,δ用于控制近邻节点的范围。
基于以上所构造的加权图,传统谱聚类的目标函数可以表示为:
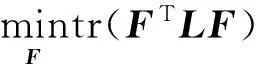

(4)
其中,tr(·)表示迹操作,F=[f1,f2,…,fn]=Y(YTY)-1/2,L=D-A为拉普拉斯(Laplacian)矩阵,其中D为对角矩阵,其每一个对象元素Dii=∑jAij。
3基于稀疏图和l2,1正则化模型的特征选择方法(SSFS)
3.1 问题提出及本文函数的构建
在传统谱聚类方法中,半监督学习模型可表示为[11]:
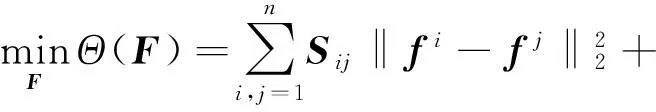

(5)
其中,F为待求解的类别标签,fi和fj是类别标签F的第i列和第j列,Sij为相似矩阵,Y为已有的类别标签,U为权重矩阵(一般而言,有监督数据的权重要大于无监督数据的权重,本文设置有监数据权重为1010,无监督数据权重为1)。
在式(5)的模型求解过程中,往往需要借助松弛方法才能得到具有连续值的类别标签[11],并且这些类别标签并不能直接用于数据分类,还需进一步借助聚类算法才能得到离散的类别标签,因此很大程度上增加了模型的计算复杂度,影响了可扩展性。为了解决这个问题,本文借助l1-范数,认为在理想情况下当邻接图中属于同一类别的两个节点xi和xj应该具有相同的类别标签[12],即fi=fj,从而使得所建立的邻接图具有稀疏特性,即:

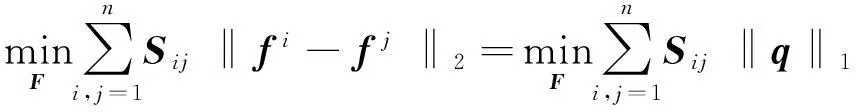
(6)
其中,q为n2维向量,该向量的第((i-1)×n+j)个元素为Sij‖fi-fj‖2。
需要注意的是,相对于文献[11]中的半监督学习模型,本文所提出的半监督学习模型借助l1-范数约束类别标签项,从而无需借助松弛方法便可得到清晰的类别标签,其学习模型的完整表示如下:


(7)
基于正则化模型的机器学习方法已经被广泛应用于特征降维、多任务学习等研究领域,并取得了较好的效果。基于正则化模型的特征选择方法可以采用以下形式描述:
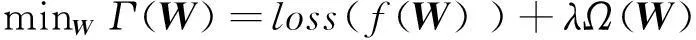
(8)
其中,W为特征选择矩阵,loss(·)为损失函数,Ω(·)为正则化模型(可以选择不同的正则化模型,如l1范数、l2范数等),参数λ为正则化参数。
为了有效避免噪声的干扰和选择有效的数据特征,本文采用正则化模型l2,1范数[12,13]。将公式(8)引入l2,1范数后,该正则化学习模型可表示:

(9)
在损失函数方面可选的方法有最小二乘法、hinge等,考虑到模型的简单性、高效性,本文选择最小二乘法作为损失函数。最后,本文结合式(7)、式(9)所提出的目标函数可表示为:

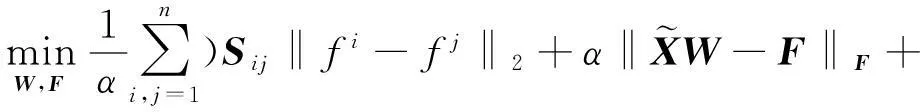
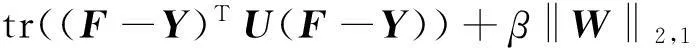
(10)

3.2 学习模型求解
求解上一小节所提出的模型(10)主要有两个难点:(1)由于该学习模型引入的l2,1和l1范数是非光滑的函数,不能直接对其进行求解;(2)尽管该学习模型中有关W和F的模型都是凸函数的,但其联合模型是非凸函数的。本文提出以下方法求解所提出的学习模型:
(1) 首先为了便于算法求解,经过简单的推导,可将目标函数(10)转换为如下形式:
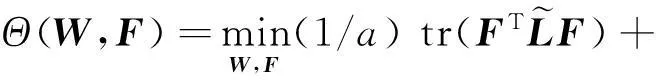
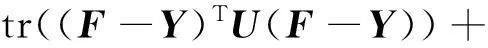

(11)


(12)
(2)锁定W不变,令(∂Θ(W,F))/∂F=0,计算式(11)可得:

(13)
转换式(13),得到:

(14)
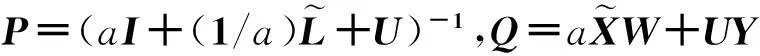
F=PQ
(15)
(3)将公式(15)代入式(11)后,令(∂Θ(W,F))/∂W=0,可得:
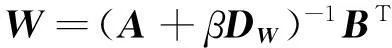

(16)
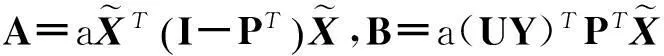
基于以上推导过程,本文提出的学习模型求解算法描述如下:
算法1SSFS
输出:特征选择矩阵W。
第1步计算初始相似矩阵S与拉普拉斯矩阵L;
第2步设置权重矩阵U;
第3步设置t=0,随机初始化特征选择矩阵W0;

第5步根据式(15)计算Ft+1;

第8步t=t+1,转至第4步直到算法收敛。
4实验结果及分析
4.1 对比算法介绍及实验数据选择
为了验证算法的有效性,本文将算法SSFS应用到多种开源数据库,包括wine[15]、breast[15]、vehicle[15]、YALE[16]、ORL[17]和jaffe[18]。表1给出了所选有关数据集的详细描述。
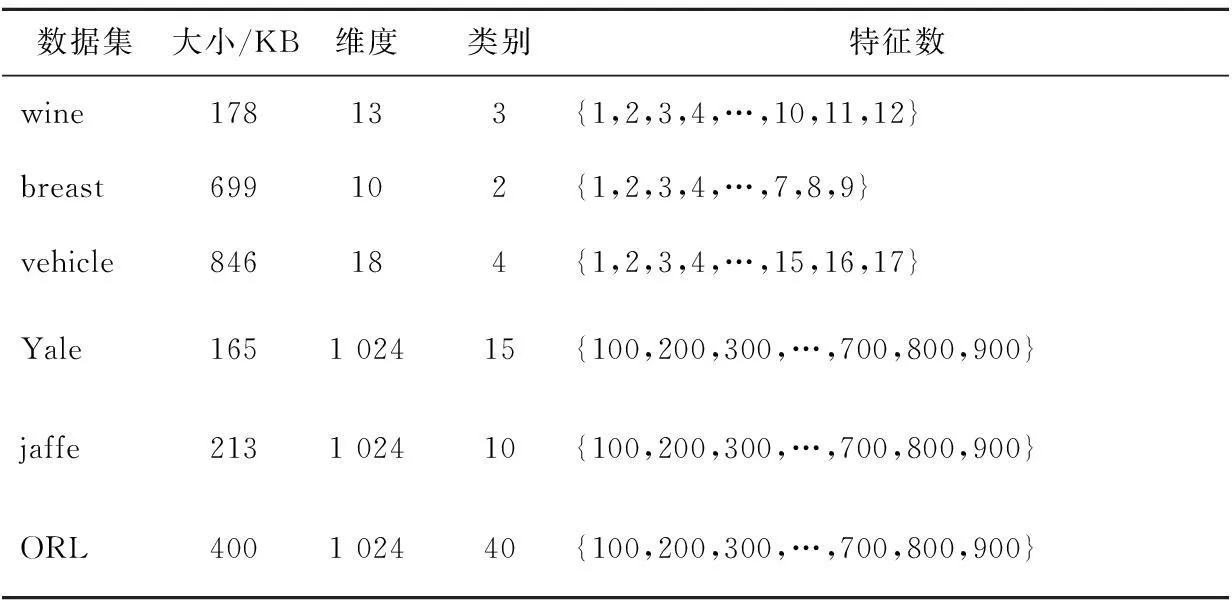
Table 1 Database description
本文挑选了几种目前流行的半监督特征选择算法进行比对分析,分类器选择SVM,相关算法描述如下:
All-features:使用所有特征作为SVM分类器的输入,其分类结果将作为本文实验的基准线。
TRCFS[10]:该方法通过引入具有抗噪声的Trace Ratio准则提高特征选择的效率。
SFSS[11]:该方法实现了特征选择和半监督学习算法的联合学习,并以数据特征之间的相关性作为特征选择的依据。
本文参照文献[11]中的参数设置方式,对于每一种算法所有涉及到的参数(如果有的话)的范围设定为{10-3,10-2,…,102,103}。对于每一种数据集,随机选取5×c个样本作为训练集,剩余样本作为测试集。最后,选择LIBSVM(Library for Support Vector Machines)作为分类工具,其中LIBSVM的最优参数采用5-fold交叉检验得到其最优值作为最终参数。每组实验数据重复五次,最后计算五次结果的平均值和标准方差。
4.2 分类准确性分析
表2为各种算法分类准确度的对比结果,图1详细给出了分类准确度随特征选择数量的变化情况。从表2和图1的实验结果可以看出,所有半监督的特征选择方法分类结果都要优于All-features,从而证明特征选择方法不但可以有效降低数据集的维度,同时也能提高数据分类的准确度。另外,本文方法要优于TRCFS和SFSS特征选择方法,从而说明对数据的类别标签进行稀疏性约束将有助于提高分类的准确度。
4.3 收敛性分析
图2表示本文算法SSFS的收敛性分析,实验中将本文算法涉及到的两个参数α和β均设置为1。从图2可以看出,本文算法经过20次左右的迭代可以达到收敛状态,从而表明本文算法具有较高的执行效率。
4.4 参数对数据集的敏感性分析
本小节对所提算法涉及到的参数α和β进行具体分析,为了节省篇幅,本文仅针对vehicle、wine和Yale等三组数据集进行分析。首先设置α=1,对数据分类结果就β和特征数量的变化情况进行分析,如图3(第一行)所示。从分析的结果可以看出,参数β的选择依赖于所选数据集,不同的数据集需要设置不同的参数。然后设置β=1并对α和特征数量的变化进行分析,如图3(第二行)所示。分析的结果表明,对于所展示的三组数据集,当参数α≤1时,可以取得较好的分类结果,由于本文目标函数的第一项用于控制数据集类别结构的稀疏度,该参数的最优取值也再次说明了稀疏的类别结构将有助于提高数据分类准确度。

Table 2 Performance comparison (ACC%±STD) of different feature selection algorithms
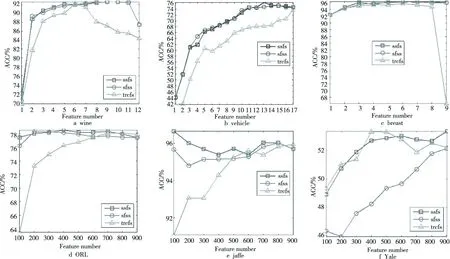
Figure 1 Classification accuracies vs. the numbers of selected features of our approach and other approaches on several datasets图1 各种算法在多种数据集上的准确度分析随特征选择数据的变化
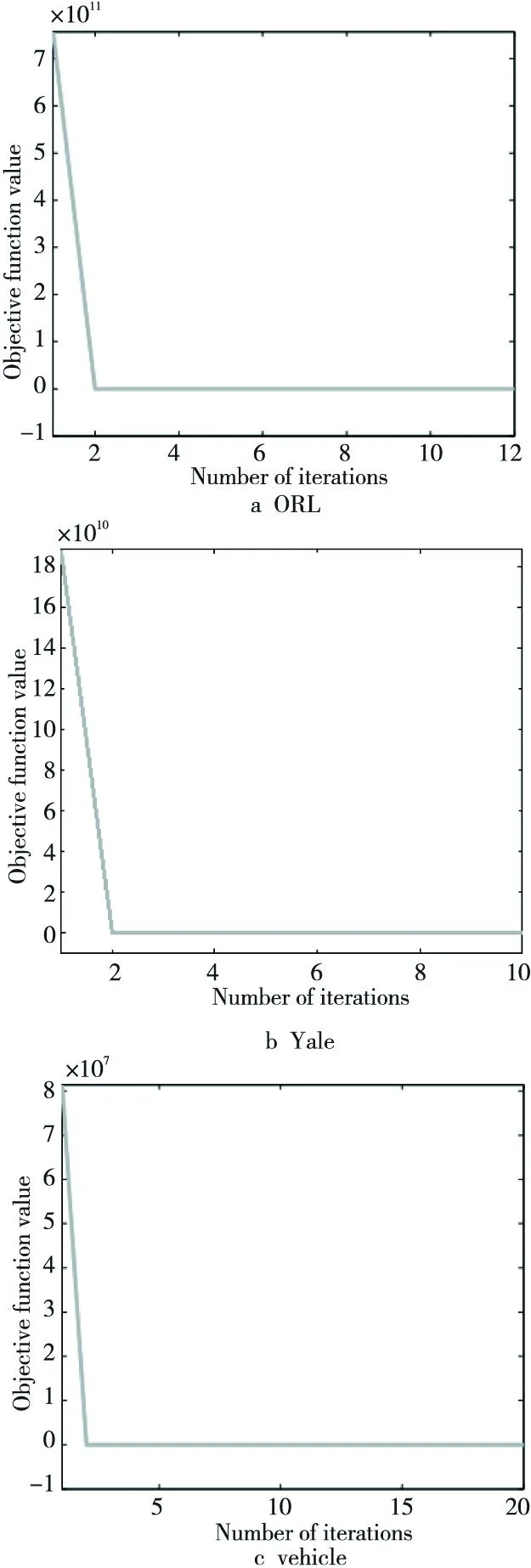
Figure 2 Convergence analysis of the SSFS图2 SSFS算法收敛性分析

Figure 3 Results of parameter sensitivity of the SSFS on different datasets图3 SSFS算法在多种数据集上的参数分析
5结束语
本文提出一种基于稀疏图表示的半监督特征选择方法,构建了类别标签和特征选择联合学习模型,并引入l2,1范数和l1范数以避免噪声的干扰和提高特征选择的准确度。由于所提出的联合学习模型具有非光滑的特点,本文还设计了一套有效的迭代方法求解模型。最后,本文将所提出的算法应用到多种开源数据集,并与目前流行的几种特征方法进行了对比分析,实验结果表明了算法的有效性。在下一步的工作中,将针对复杂事件检测的应用领域对所提出算法进行深入研究。
参考文献:附中文
[1]Xie Juan-ying, Xie Wei-xin. Several feature selection algorithms based on the discernibility of a feature subset and support vector machines[J].Chinese Journal of Computer,2014,37(8):1704-1718. (in Chinese)
[2]Jian Cai-ren,Chen Xiao-yun. Unsupervised feature selection based on locality preserving projection and sparse representation [J]. Pattern Recognition and Artificial Intelligence,2015,28(3):247-252. (in Chinese)
[3]Yang Y,Ma Z G,Hauptmann A G,et al. Feature selection for multimedia analysis by sharing information among multiple tasks[J]. IEEE Transactions on Multimedia,2013,15(3):661-669.
[4]Ren Y Z,Zhang G J,Yu G X,et al. Local and global structure preserving based feature selection[J]. Neurocomputing,2012,89:147-157.
[5]He X F,Cai D,Niyogi P. Laplacian score for feature selection[M]∥Advances in Neural Information Processing Systems. Cambridge:MIT Press,2006:507-514.
[6]Cai D,Zhang C,He X F. Unsupervised feature selection for multi-cluster data[C]∥Proc of the 16th International Conference on Knowledge Discovery and Data Mining ACM SIGKDD,2010:333-342.
[7]Zhao Z,Wang L,Liu H. Efficient spectral feature selection with minimum redundancy[C]∥Proc of the 24th Conference on Artificial Intelligence AAAI,2010:673-678.
[8]Li Z C,Yang Y,Liu J,et al. Unsupervised feature selection using nonnegative spectral analysis[C]∥Proc of the 26th Conference on Artificial Intelligence AAAI,2012:1026-1032.
[9]Doquire G,Verleysen M. A graph Laplacian based approach to semi-supervised feature selection for regression problems[J]. Neurocomputing,2013,121:5-13.
[10]Liu Y,Nie F,Wu J,et al. Efficient semi-supervised feature selection with noise insensitive trace ratio criterion[J]. Neurocomputing,2013,105:12-18.
[11]Ma Z,Nie F,Yang Y,et al. Discriminating joint feature analysis for multimedia data understanding[J]. IEEE Transactions on Multimedia,2012,14(6):1662-1672.
[12]Shuman D I,Wiesmeyr C,Holighaus N,et al. Spectrum-adapted tight graph wavelet and vertex-frequency frames[J]. IEEE Transactions on Signal Processing,2015,63:4223-4235.
[13]Yang Y,Shen H T,Ma Z G,et al.l2,1-norm regularized discriminative feature selection for unsupervised learning[C]∥Proc of the 22nd International Joint Conference on Artificial Intelligence,2011:1589-1594.
[14]Nie F,Wang H,Huang H,et al. Unsupervised and semi-supervised learning vial1-norm graph[C]∥Proc of IEEE International Conference on Computer Vision,2011:2268-2273.
[15]Asuncion A,Newman D. UCI machine learning repository. University of California,Irvine,School of Information and Computer Sciences,2007[EB/OL].[2015-06-01].http://www.ics.uci.edu/~mlearn/MLRepository.html.
[16]Han Y,Xu Z,Ma Z,et al. Image classification with manifold learning for out-of-sample data[J]. Signal Processing,2013,93(8):2169-2177.
[17]He X F, Cai D,Yan S C,et al. Neighborhood preserving embedding[C]∥Proc of the 10th IEEE International Conference on Computer Vision,2005:1208-1213.
[18]Lyons M J,Budynek J,Akamatsu S. Automatic classification of single facial images[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,1999,21(12):1357-1362.
[1]谢娟英,谢维信. 基于特征子集区分度与支持向量机的特征选择算法[J]. 计算机学报,2014,37(8):1704-1718.
[2]简彩仁,陈晓云. 基于局部保持投影和稀疏表示的无监督特征选择方法[J]. 模式识别与人工智能,2015,28(3):247-252.

王晓栋(1983-),男,山西平遥人,硕士,讲师,CCF会员(22248M),研究方向为模式识别和图像处理。E-mail:xdwangjsj@xmut.edu.cn
WANG Xiao-dong,born in 1983,MS,lecturer,CCF member(22248M),his research interests include pattern recognition, and image processing.

严菲(1985-),女,湖南岳阳人,硕士,实验师,研究方向为数据挖掘和数据隐藏。E-mail:fyan@xmut.edu.cn
YAN Fei,born in 1985,MS,experimentalist,her research interests include data mining, and data hiding.

谢勇(1985-),男,湖南衡山人,博士,讲师,研究方向为嵌入式系统和CPS。E-mail:yongxie@xmut.edu.cn
XIE Yong,born in 1985,PhD,lecturer,his research interests include embedded system, and cyber-physical system.

江慧琴(1979-),女,福建邵武人,博士,讲师,研究方向为嵌入式系统和模式识别。E-mail:hqjiang@nudt.edu.cn
JIANG Hui-qin,born in 1979,PhD,lecturer,her research interests include embedded system, and pattern recognition.
A feature selection method based on sparse graph representation
WANG Xiao-dong,YAN Fei,XIE Yong,JIANG Hui-qin
(College of Computer and Information Engineering,Xiamen University of Technology,Xiamen 316024,China)
Abstract:Feature selection, which aims to reduce data’s dimensionality by removing redundant features, is one of the main issues in the field of machine learning. Most of existing graph-based semi-supervised feature selection algorithms are suffering from neglecting clear cluster structure. We propose a semi-supervised algorithm based on l1-norm graph in this paper. A joint learning framework is built upon cluster structure and feature selection; l1-norm is imposed to guarantee the sparsity of the cluster structure, which is suitable for feature selection. To select the most relevant features and reduce the effect of outliers, the l2,1-norm regularization is added into the objective function. We evaluate the performance of the proposed algorithm over several data sets and compare the results with state-of-the-art semi-supervised feature selection algorithms. The results demonstrate the effectiveness of the proposed algorithm.
Key words:feature selection;semi-supervised learning;l2,1-norm;l1-norm
作者简介:
doi:10.3969/j.issn.1007-130X.2015.12.027
中图分类号:TP391.4
文献标志码:A
基金项目:国家自然科学基金资助项目(61502405);福建省教育厅中青年教师教育科研资助项目(JA15385,JA15368);厦门理工学院对外科技合作专项资助项目(E201400400)
收稿日期:修回日期:2015-10-11
文章编号:1007-130X(2015)12-2372-07
