Buck-Boost变换器中分叉与混沌现象的研究

孙　影，齐凤河，宋宏明

(大庆师范学院 机电工程学院，黑龙江 大庆 163712)



Buck-Boost变换器中分叉与混沌现象的研究

孙影，齐凤河，宋宏明

(大庆师范学院 机电工程学院，黑龙江 大庆 163712)

摘要：在查阅相关文献的基础上，根据电流模式Buck-Boost变换器的工作情况，分析了其状态方程，根据闪频映射对电流模式Buck-Boost变换器中电容电压和电感电流进行采样，推导了精确离散迭代映射模型，并在MATLABM文件中编写程序得到其分叉图、庞加莱映射、输出电压的离散值，这些仿真结果均证明了电流模式Buck-Boost变换器中存在分叉和混沌现象。

关键词：Buck-Boost变换器；混沌；分叉

0引言

近些年以来，开关变换器在工业自动化等领域有着广泛的应用，工程师们深入研究了其中的动力学行为，对电路的参数选择进行了优化，从而获得最佳的性能[1-2]。目前，对Buck变换器和Boost变换器中非线性现象的研究比较多，但对Buck-Boost变换器中分叉和混沌现象研究并不多，本文针对电流模式Buck-Boost变换器中分叉和混沌现象进行了研究，通过MATLAB软件仿真分析表明该变换器中存在丰富的分叉与混沌现象。

1电流模式Buck-Boost变换器工作原理

电流模式Buck-Boost变换器的工作原理框图如图1所示[3]。图中iL是电感电流，Iref是参考电流，vC是电容电压。

图1　Buck-Boost变换器的工作框图

当该变换器工作在电感电流连续模式下，只有两种状态，即切换开关S闭合和关断，根据电路中的KCL和KVL定律列写其微分方程，其中，忽略了电感和电容的寄生效应来简化模型的推导。

当S闭合时，状态方程为：

(1)

(2)

当S断开时，状态方程为：

(3)

(4)

2精确离散迭代映射模型

采用闪频映射对电流模式Buck-Boost变换器系统中电感电流和电容电压状态变量进行采样，进而得到系统的精确离散迭代映射模型。假设开关闭合时在一个时钟脉冲内电感电流iL=in，vC=vn，由闪频映射可知，当iL=Iref时，开关S导通，导通时间tn根据式(1)可得：

(5)

因此，导通时间tn为

(6)

由公式(2)可知：电容电压vC(tn)：

(7)

根据电流模式Buck-Boost变换器状态方程和采样方程可知，该变换器的精确离散迭代映射模型可以分为以下两种情况：

当tn≥T时，在一个时钟周期内，开关S一直处于闭合状态，in和vn作为下一个时钟的初始值，则：

(8)

(9)

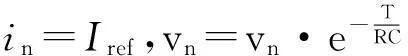
(10)

由式(10)中R、L、C的不同值可分为以下几种情况：

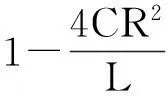
in+1=c1er1(T-tn)+c2er2(T-tn)

(11)

vn + 1= -L[c1r1r1(T-tn) +c2r2er2(T-tn)]

(12)

其中：

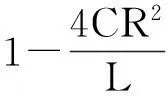
in+1=[c1+c2(T-tn)]er2(T-tn)

(13)

vn+1=-Ler1(T-C)[c2+c1r1+c2r2(T-tn)]

(14)

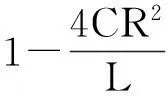
in+1=eα(T-tn)[c1cosβ(T-tn)+c2sinβ(T-tn)]

(15)

vn+1=-Leα(T-tn)[(c1α+c2β)cosβ(T-tn)+(c2α-c1β)sinβ(T-tn)]

(16)

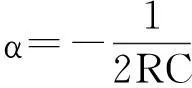
3电流模式Buck-Boost变换器分叉与混沌现象

根据我们推导的精确离散迭代映射模型通过MATLAB软件来研究电流模式Buck-Boost变换器中的非线性现象，即分叉与混沌现象。从理论上来说，电路中任何参数都可以作为分叉参数，如输入电压、负载电阻、参考电流等等。本文以参考电流作为分叉参数来绘制电流模式Buck-Boost变换器的分叉图，并分析不同工作状态下的庞加莱映射以及电容电压的离散值。

通过在MATLAB的M文件中编程，电流模式Buck-Boost变换器的电容电压随参考电流变化的分叉图如图2所示。

图2　参考电流为变化参数时电流模式Buck-Boost变换器的分叉图

从图2所示，在电流模式Buck-Boost变换器中，参考电流从0.8A到4.5A的过程中，其经历了1周期状态、2周期状态、4周期状态和8周期状态，最终进入混沌状态。在参考电流为1.1A时，电流模式Buck-Boost变换器发生第一次分叉，同时进入2周期状态；当参考电流增加到1.6A时，电流模式Buck-Boost变换器进入4周期状态；当参考电流为1.9A时，由4周期状态进入到了8周期状态；当参考电流增加到2.1A时，由8周期状态进入到了混沌状态。所以电流模式Buck-Boost变换器通过倍周期轨迹进入混沌状态。

当参考电流为1A时，电流模式Buck-Boost变换器的庞加莱映射如图3所示，电容电压的离散值如图4所示。

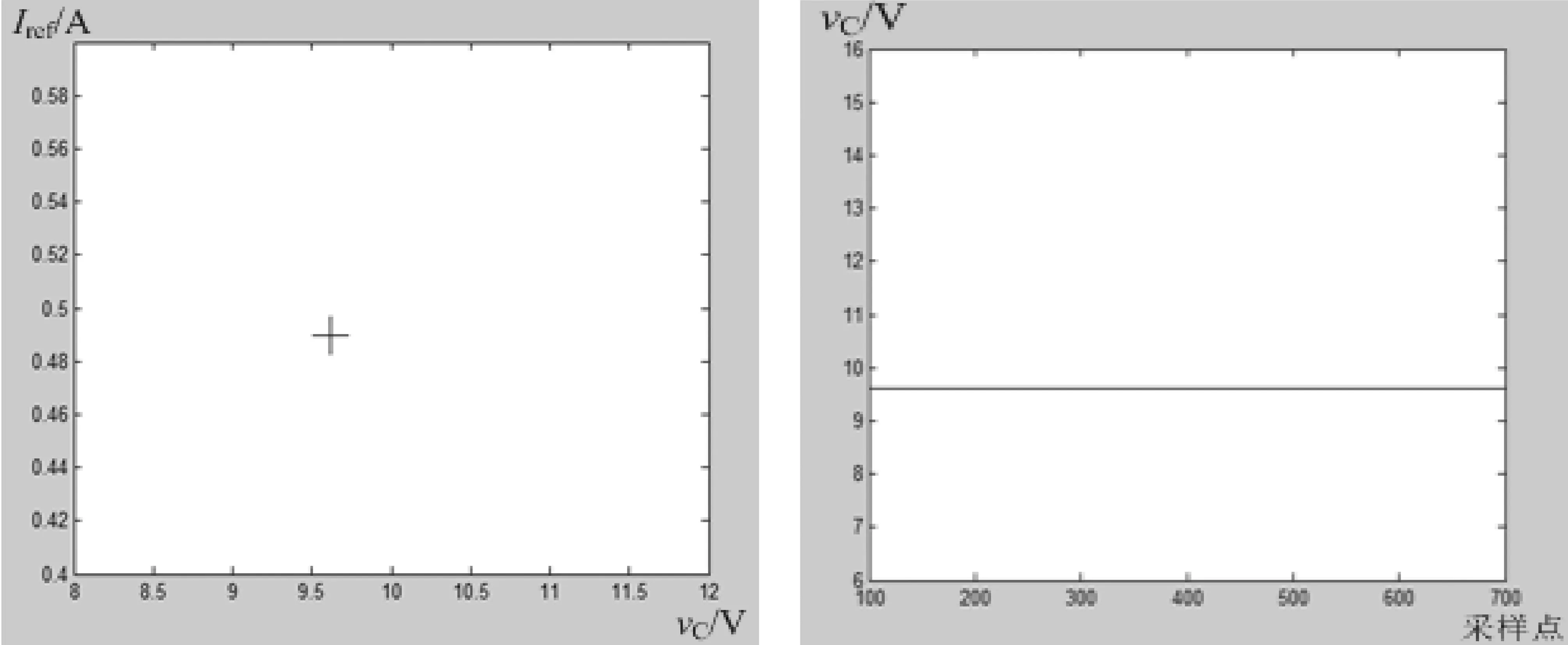
图3　庞加莱映射　　　　　　 图4　电容电压的离散值

当参考电流为1.8A时，电流模式Buck-Boost变换器的庞加莱映射如图5所示，电容电压的离散值如图6所示。

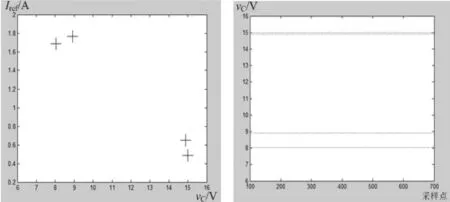
图5　庞加莱映射　　　　　图6　电容电压离散值

当参考电流为2A时，电流模式Buck-Boost变换器的庞加莱映射如图7所示，电容电压的离散值如图8所示。

图7　庞加莱映射　　　　　图8　电容电压离散值

当参考电流为2.5A时，电流模式Buck-Boost变换器的庞加莱映射如图9所示，电容电压的离散值如图10所示。

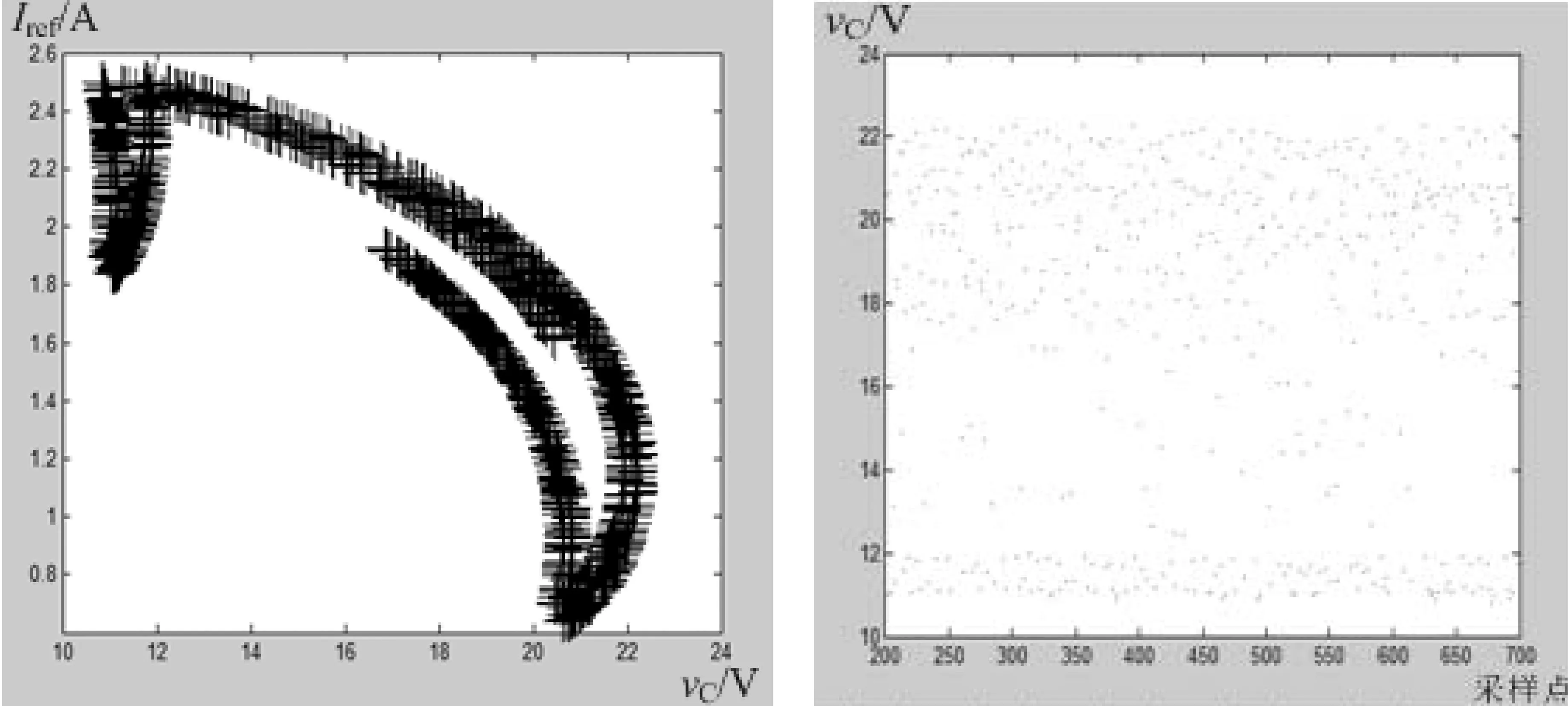
图9　庞加莱映射　　　　图10　电容电压离散值

从图3到图10可知：电流模式Buck-Boost变换器中不同的参考电流所对应的庞加莱映射和电容电压离散值与其分叉图有很好的一致性，不同的参考电流时，电流模式Buck-Boost变换器处于不同的周期状态。

4结束语

本文研究了电流模式Buck-Boost变换器中的分叉与混沌现象，根据它的状态方程，并采用闪频映射对其电容电压和电感电流进行采样，推导了其精确离散迭代映射模型，分析了不同参考电流的条件下，该变换器中是否有分叉和混沌现象。根据电流模式Buck-Boost变换器的精确离散迭代映射模型，通过在MATLAB中的M文件编程得到其分叉图、庞加莱映射、电容电压的离散值，由分叉图所分析的电流模式Buck-Boost变换器所处的工作周期状态与其庞加莱映射、电容电压的离散值一致，根据这些仿真图皆证明了电流模式Buck-Boost变换器中存在丰富的分叉和混沌现象。

[参考文献]

[1]谢玲玲，龚仁喜，王旷，等. 电流模控制Buck-Boost变换器非线性行为研究[J]. 电测与仪表，2010,47(5)：4-7.

[2]金爱娟，尹鹏鸿，夏震，等. 电流型Buck-BoostDC-DC变换器的分岔与混沌[J]. 上海理工大学学报，2013,35(3)：299-301,306.

[3]袁雷，沈建清，肖飞. 电流模式控制Buck-Boost变换器建模及非线性现象仿真[J]. 中南大学学报：自然科学版，2012,43 (3)：972-979.

中图分类号：TP368.1

文献标识码：A

文章编号：2095-0063(2015)06-0006-04

收稿日期：2014-12-03

作者简介：孙影( 1987-)，女，黑龙江大庆人，助理实验师，从事检测技术及自动化研究。

DOI10.13356/j.cnki.jdnu.2095-0063.2015.06.002