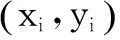基于蜂窝网格的变步长移动节点部署算法*

朱明，金仁成，车志平，李应琛

(大连理工大学 辽宁省微纳米技术及系统工程重点实验室，大连 116024)

* 基金项目：国家重点基础研究发展计划(973计划)资助项目(2009CB320300)；国家“十二五”科技支撑计划资助项目(2011BAG05B02)。



基于蜂窝网格的变步长移动节点部署算法*

朱明，金仁成，车志平，李应琛

(大连理工大学 辽宁省微纳米技术及系统工程重点实验室，大连 116024)

* 基金项目：国家重点基础研究发展计划(973计划)资助项目(2009CB320300)；国家“十二五”科技支撑计划资助项目(2011BAG05B02)。

摘要:针对无线传感器网络节点部署问题，提出了一种基于蜂窝网格的变步长节点部署算法。将监测区域进行正六边形网格划分，利用网格中心位置信息，以及随机散布的节点的位置信息，每个节点会找到自己的目标网格，目标网格中心即为该节点部署位置。根据待部署节点与相应目标网格顶点之间的距离信息，控制节点的移动距离。仿真结果表明，该算法收敛速度快，能以较小的节点平均移动距离获得98%以上的覆盖率。

关键词:无线传感器网络；节点部署；蜂窝网格

引言

无线传感器网络(WSN)节点部署，是在指定的监测区域内，适当布置传感器节点以满足特定需求，传感器节点布置的好坏直接影响WSN所能提供的“感知”服务质量[1]。

一种能够有效控制节点的移动策略是借助虚拟力原理导向控制节点移动[2-4]。节点受监测区域内其他节点的虚拟引力和斥力的作用而移动，合力为0时，停止移动。基于虚拟力的算法能够有效提高监测区域覆盖率，但因为节点没有移动目标，容易形成监测空洞。

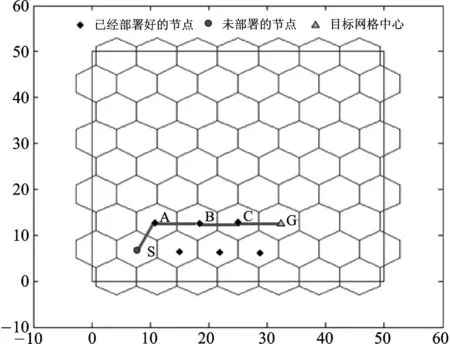
参考文献另一种就是借助网格划分的策略，从节点的覆盖效率出发，实现监测区域的节点部署。[5]首次提出当且仅当3个半径为1的圆交于一点，且三个圆心连成边长为的等边三角形时，可以获得最大的覆盖效率。参考文献[6]在最大覆盖效率的基础上，提出了基于蜂窝网格的传感器节点静态部署算法，将无线传感器网络节点部署在组成蜂窝网格的各个六边形的中心。参考文献[7]将网格划分与虚拟力算法有机结合，提出了一种基于网格划分的虚拟力部署算法，但是，该算法没有在全局上从最短距离开始寻找，会出现能耗过多的情况。参考文献[8]利用满足全覆盖条件的正六边形蜂窝网络拓扑模型，将监测区域划分成正六边形的网格结构，在正六边形的中心设置虚拟锚节点，结合传统的虚拟力算法，考虑虚拟锚节点的引力作用，同时兼顾不同移动节点间的斥力影响，在满足一定覆盖率要求的前提下,建立节点在合力作用下的移动到虚拟锚节点的运动模型。 利用[5-6]中提到的部署模型，对监测区域进行网格划分，得到如图1所示的蜂窝网络结构，这样就很容易得到蜂窝网络中每个正六边形网格的中心坐标。图中正六边形网格的边长为节点的感知半径，当节点处于各个网格的中心时，即为参考文献[6]所述的静态网络结构，传感器节点的覆盖效率最高，达到82.7%。

针对传统基于虚拟力的移动策略移动目标不明确、能耗过大，以及容易出现监测漏洞等缺点，提出了一种基于蜂窝网格的变步长节点部署算法。利用监测区域的正六边形网格划分信息，以及随机散布的节点位置信息，每个节点会找到自己的目标网格。根据待部署节点与相应目标网格中心之间的距离信息，控制节点的移动距离和方向。

1问题陈述

1.1相关假设

针对本文的研究，做出以下假设：

① 所有的传感器节点具有相同的感知、通信、计算以及移动能力；

② 所有的传感器节点的感知范围和通信范围都是理想的圆形；

③ 所有节点都能通过GPS等方法获取自身位置信息，另外，当监测区域划分为蜂窝网状结构时，每个正六边形网格的中心坐标信息是可以获取的；

④ 节点的初始部署是随机的；

⑤ 传感器节点的通信半径Rc是其感知半径Rs的2倍，此时，覆盖可保证连通[9]；

⑥数据传输过程中的延时等误差忽略不计。

1.2感知模型

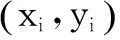
为简化问题研究，选择传感器节点的模型为二元感知模型。当点si与P之间的距离在节点的感知范围内时，节点能采集到P点信息的概率为1；当点si与P之间的距离在节点的感知范围外时，节点能采集到P点信息的概率为0，如下所示：

1.3评价方法

为了评价算法的优劣，引入3个评价机制：覆盖率、平均移动距离、部署时间。

(1) 覆盖率

覆盖率是评价一个部署策略最重要的指标,它从直观上表达了一个部署策略的好坏。对一些特殊的监测区，需要很高的覆盖率，同时还要避免出现监测空洞。覆盖率越大，节点对监测区域的监测效果越明显，部署策略的优越性越强。在数学上，覆盖率是所有节点覆盖区域面积的并集与监测区域面积的比值，如下所示：

式中，Ai是每个节点的覆盖面积，A是监测区域的面积，Coverage(%)是监测区域的覆盖率。

(2) 平均移动距离

平均移动距离体现了每个节点在部署过程中移动距离的多少。由于节点在移动过程中需要消耗能量，平均移动距离也间接反映节点在部署过程中消耗能量的平均水平。平均移动距离越小，节点的平均能耗越低。当节点部署策略实施完成，可以利用式(4)来计算节点的平均移动距离。

(3) 部署时间

在对时间要求严格的场合,部署时间是非常重要的指标。在本文中，部署时间定义为从初始节点随机散布到所有节点部署完成的这段时间。部署时间的长短与部署策略的关系很大，它能反映一个部署策略的好坏。

2本文算法

2.1基本网格划分结构

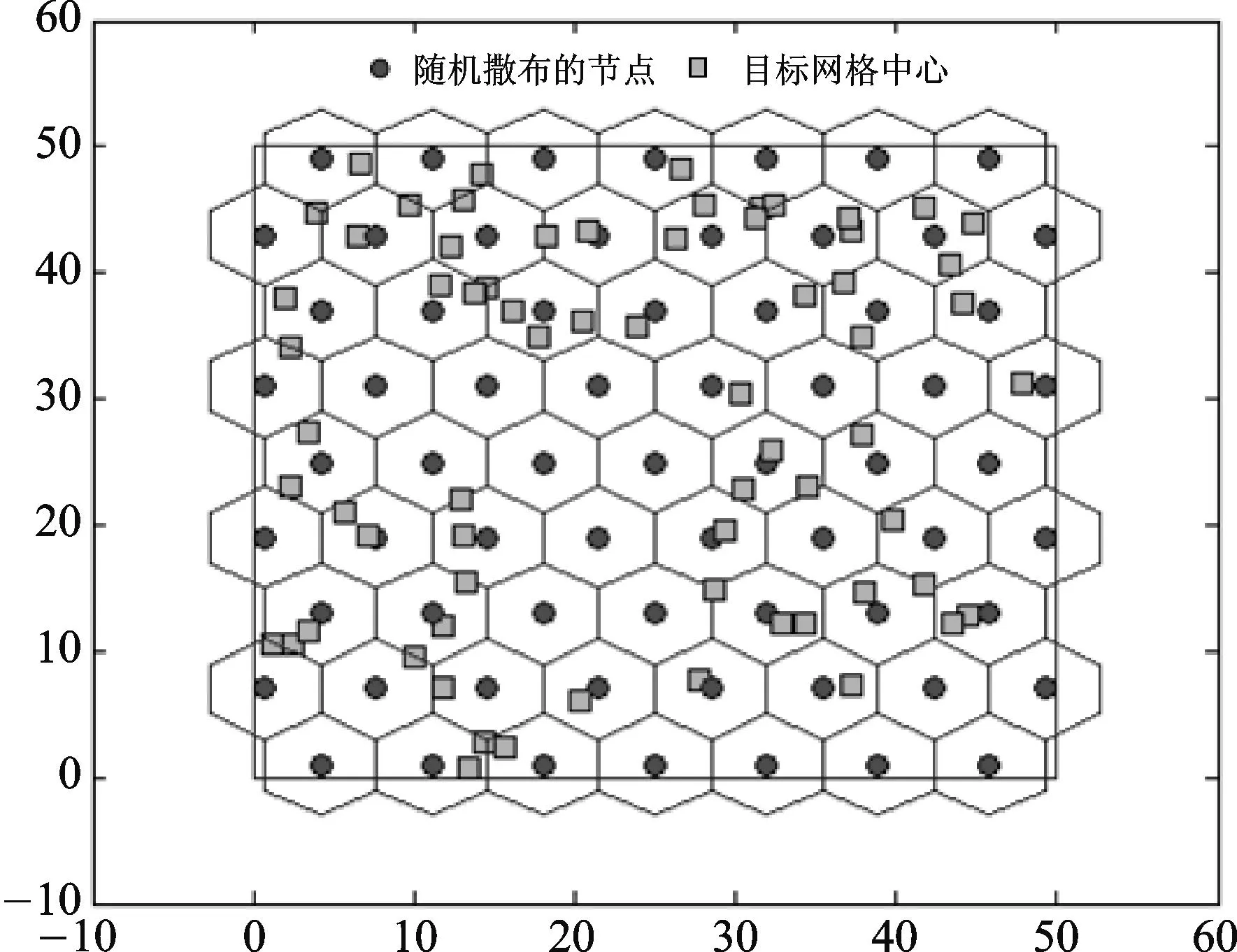
图1　监测区域的基本网格结构

2.2基于蜂窝网格的变步长部署策略

按照图1所示的基本网状结构，将各个正六边形网格的中心作为随机散布的移动传感器节点的移动目标。当节点随机散布后，根据最小距离原则在全局上分配每个传感器节点的目标网格，当所有节点选择目标网格点之后，节点移动开始。

(1) 节点移动目标选择

当传感器节点随机散布后，利用节点位置信息、正六边形网格中心坐标信息，可以计算出每个传感器节点与图1中任意一个正六边形网格中心之间的距离信息，将其记作一个m×n的矩阵Dm,n，如下所示：

式中，m是随机散布的传感器节点的个数，n是监测区域划分得到的正六边形网格的个数，矩阵中的每一行元素代表传感器节点i到n个正六边形网格之间的距离。对矩阵中的元素进行查找，确定每个传感器节点的目标网格，处理过程如下：

① 对距离矩阵中的所有元素进行第一轮查找，找到其中最小的元素dij，由此确定第i个节点的目标网格为网格j，并标记节点i已确定为目标网格，第i行和第j列的所有元素不参与下次查找;

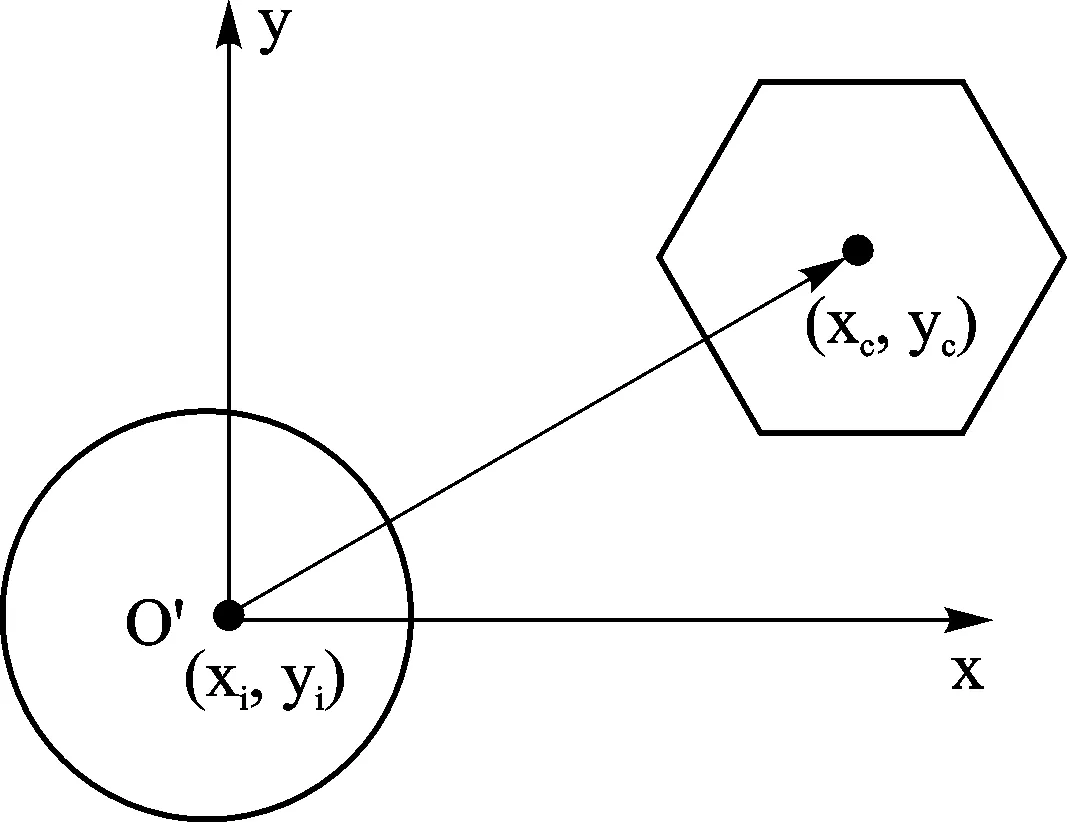
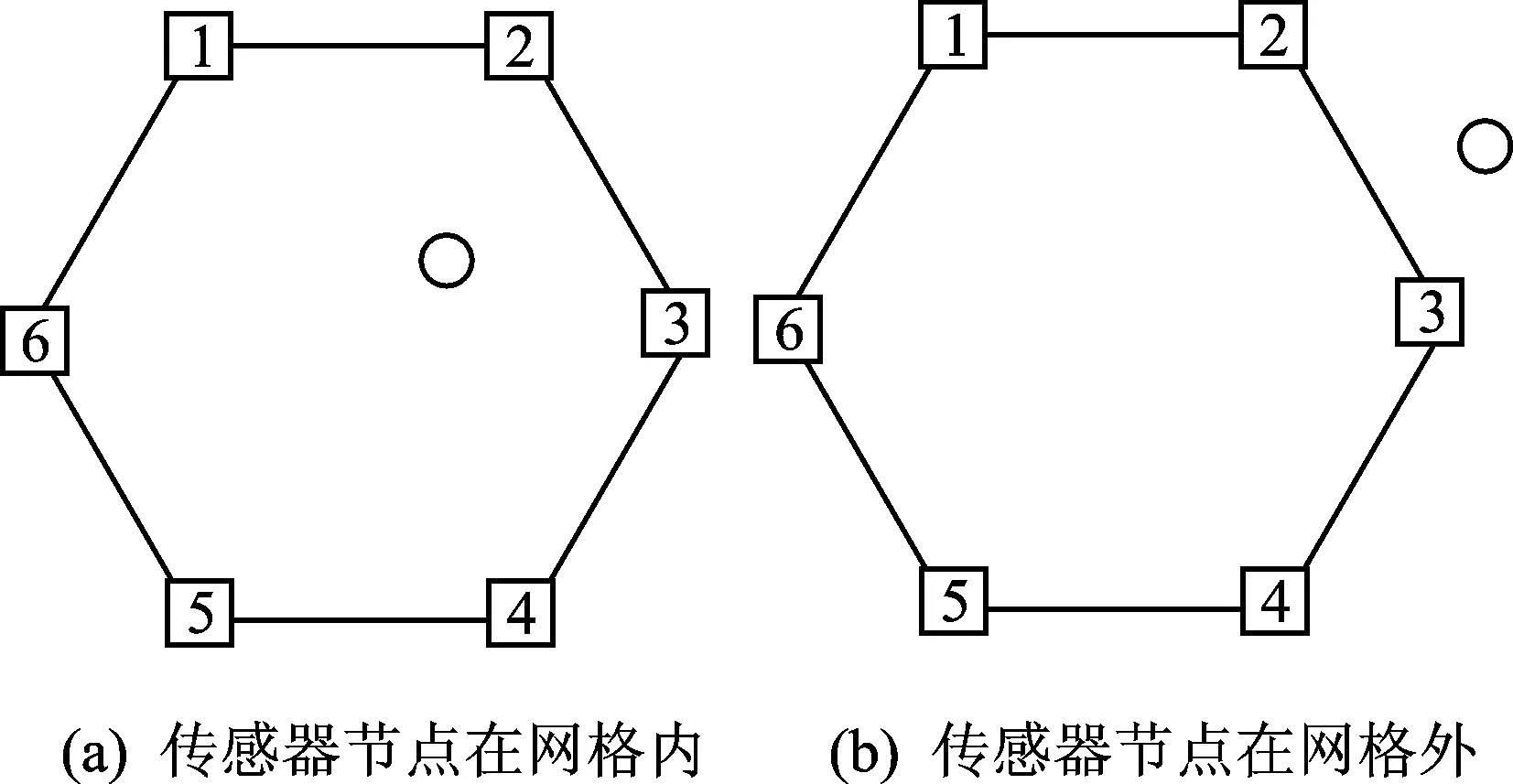
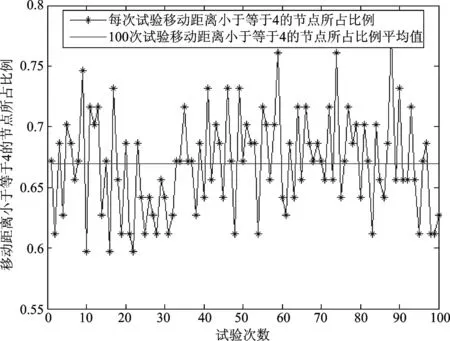
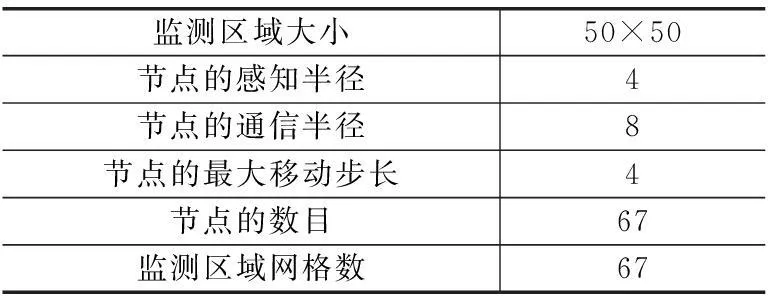
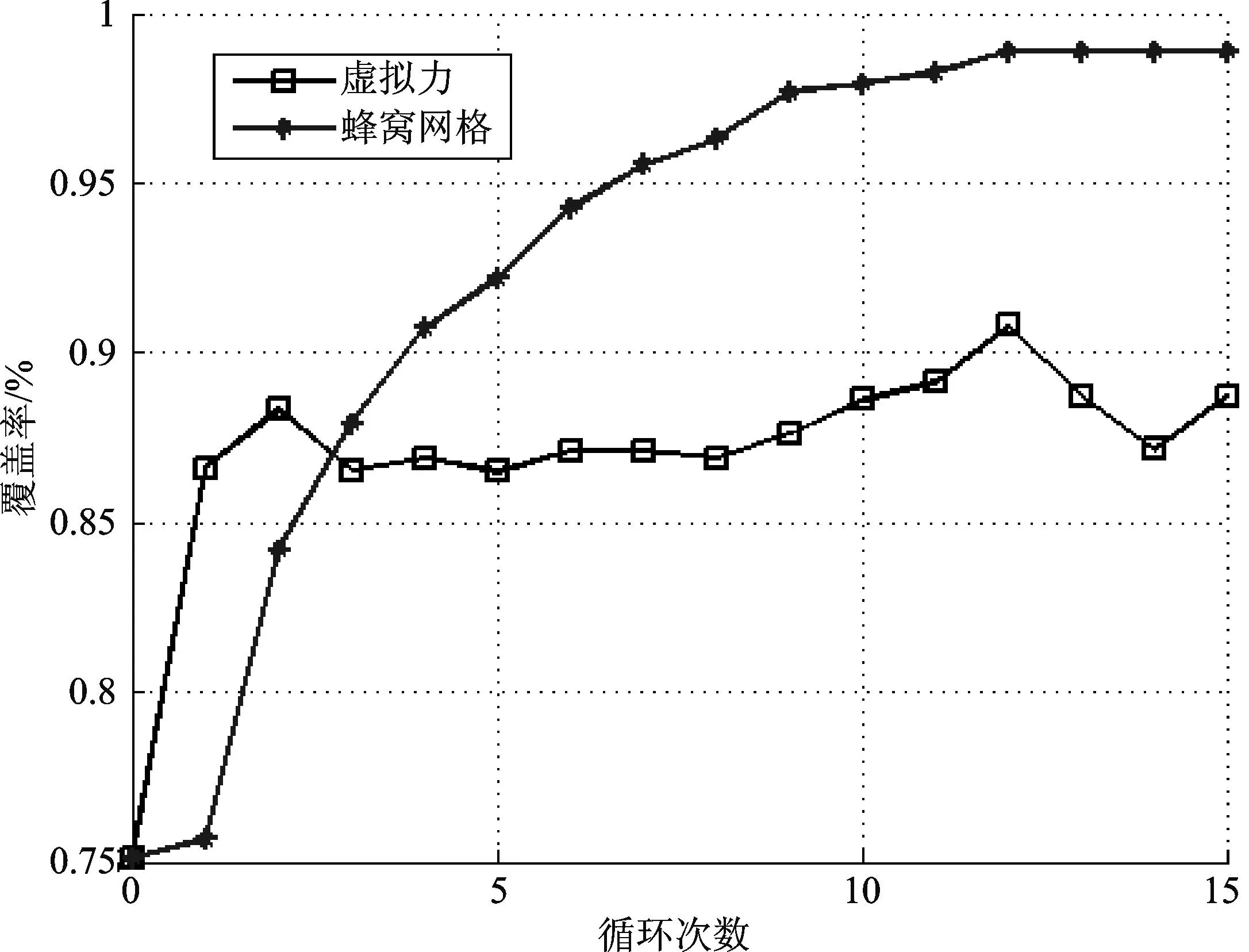
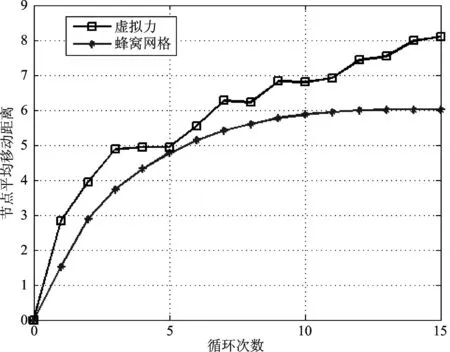
② 如果i

③ 节点的移动目标选择完成，查找过程结束。

(2) 确定节点移动方向α及每次移动距离Mov_D

图2　节点与其目标网格坐标方位图

显然，由二者的坐标信息可以计算出节点的移动方向角α，如下所示：

为了得到比较完善的部署控制策略，需要研究传感器节点在部署过程中移动距离的选择。如图3所示，方格代表的是正六边形的顶点，方格内部的数字是顶点的编号，圆圈代表的是传感器网络节点。显然，传感器节点与目标网格的位置关系不确定，既可在网格内部，也可在网格外部。若节点与目标网格中心的距离大于最大移动步长，则需要先对节点以最大步长进行移动，直到节点与目标网格中心的距离小于最大移动步长，则以当前距离为移动步长；若节点与目标网格中心的距离小于最大移动步长时，以当前距离作为节点的移动步长。以d表示节点与其目标网格点之间的距离，Max_Step为最大移动步长，Mov_D为每次移动距离，则每次移动距离的选择如下所示：

图3　节点与其目标网格之间的包含关系

(3) 考虑避障问题的部署策略研究

在节点的部署过程中，节点之间相互碰撞的可能性不可忽略,特别在基于移动机器人的节点部署场合，当初始部署阶段具有很高的速度时，节点间的相互碰撞会造成节点不可修复的损坏。因此，对节点避障策略的研究是非常有必要的。

针对节点之间会产生碰撞的问题，提出了一种基于接替移动法的避障策略。为了更好地说明该避障策略，先对节点与其目标网格之间的距离进行数学统计，如图4所示。

图4　对节点与其目标网格中心距离的数学统计

经过统计发现，67%的传感器网络节点的移动距离小于或等于4，即位于其目标网格内部。显然，由于是从全局上进行目标网格查找，该节点与相应的目标网格中心之间不会再有其他的传感器节点，否则该网格并不是该节点对应的目标网格。

经过以上分析，可以得到以下的部署策略：

① 部署处于其目标网格内的节点，一次移动到达相应的目标网格中心，这类节点部署完毕。

② 部署节点处于其目标网格外部的节点，如图5所示，首先查找节点S与其目标网格G之间的一系列已经部署的节点A、B、C…，以这些节点为基础，优先选择之前移动距离较小的节点建立移动路径，将节点S向目标网格G的移动转化为C→G，B→C，A→B，S→A的移动过程，在整个移动过程中，节点的每次移动先以最大移动步长Mov_Step移动，直到与目标网格中心的距离小于最大移动步长时，再以当前距离作为节点的移动步长。

图5　部署处于其目标网格点外部节点的路径选择

3仿真结果

为了验证算法的优越性，借助Matlab对上述算法进行仿真试验。在试验中，设定传感器节点的相关参数如表1所列。

表1　传感器节点的相关参数

在基于蜂窝网格的节点部署策略的仿真试验中，首先开始移动的是处于目标网格内部的节点，一次移动达到目标网格中心；接着运用考虑避障的部署策略移动处于目标网格外部的传感器节点。从图6可以看出，基于蜂窝网格的部署算法获得的覆盖率，在第一次部署得到的覆盖率低于虚拟力算法得到的覆盖率，但是在第4次循环迭代以后有明显增加的趋势，在第7次循环迭代后覆盖率达到95%以上，明显高于虚拟力算法获得的最高90%左右的覆盖率。更重要的是，从图7中可以看出，基于蜂窝网格策略的部署算法中，节点的最大平均移动距离为6 m，相比虚拟力算法中的8 m有所减小。

图6　监测区域在不同算法下得到的覆盖率

图7　节点的平均移动距离

结语

[1] Li J H,Yu M.Sensor coverage in wireless ad hoc sensor networks[J].International Journal of Sensor Networks,2007,2(3-4):218-229.

[2] Zou Y,Chakrabarty K.Sensor deployment and target localization based on virtual forces[C]//INFOCOM,2003.

[3] 周浦城,崔逊学,王书敏,等.基于虚拟力的无线传感器网络覆盖增强算法[J].系统仿真学报,2009(5):1416-1419.

[4] 周彤,洪炳.基于虚拟力的混合感知网节点部署[J].计算机研究与发展,2015,44(6):965-972.

[5] 曹峰,刘丽萍,王智.能量有效的无线传感器网络部署[J].信息与控制,2006,35(2):147-153.

[6] 凡志刚,郭文生,桑楠.一种基于蜂窝网格的传感器节点部署算法[J].传感器与微系统,2008(4):15-17.

[7] 李贤,何启丽,唐秋玲,等.一种基于网格划分的虚拟力部署算法的研究[J].广西大学学报:自然科学版,2013,37(6):1164-1169.

[8] 钱开国,王伟,申时凯,等.基于蜂窝网格锚点的虚拟力导向节点部署算法[J].计算机测量与控制,2014,22(6):1839-1841.

[9] Zhang H,Hou J C.Maintaining sensing coverage and connectivity in large sensor networks[J].Ad Hoc&Sensor Wireless Networks,2005,1(1-2):89-124.

(责任编辑：薛士然收修改稿日期：2015-06-29)

Sensor Deployment Algorithm with Variable Step Size Based on Hexagonal Grid

Zhu Ming,Jin Rencheng,Che Zhiping,Li Yingchen

(Key Laboratory for Micro/Nano Technology and System of Liaoning Province,Dalian University of Technology,Dalian 116024,China)

Abstract：To solve the issue of wireless sensor network deployment,a sensor deployment algorithm with variable step size based on hexagonal grid is proposed.The monitoring field is drawn into regular hexagonal grids.Using the location information of each hexagon’s center and the random deployed sensor nodes,each node’s targeting grid can be found.The node should be deployed at the targeting grid’s center.Based on the distance between the deploying nodes and the targeting grid’s center,the move step can be selected.The simulation results show that the proposed algorithm can achieve a coverage of 98% with a faster convergence speed and a lower average moving distance.

Key words:wireless sensor network;sensor deployment;hexagonal grid

中图分类号:TP393.17

文献标识码:A