石灰石直接硫化模型研究

白子为,王春波

(华北电力大学 能源动力与机械工程学院，河北保定071003)

石灰石直接硫化模型研究

白子为,王春波

(华北电力大学 能源动力与机械工程学院，河北保定071003)

摘要：在燃煤污染物控制方法中干法脱硫因其投资少、控制简单而应用广泛，而价格低廉，脱硫效果好的石灰石也成为了钙基脱硫剂的首选。目前对于直接硫化的描述模型还未有广泛共识。在传统煅烧硫化模型基础上，引入了Knudsen扩散、烧结和多种扩散方式并存观点等约束完善模型，提出了一种新型的石灰石直接硫化模型。并结合实验数据进行验证，结果分析表明烧结与多种扩散并存观点的假设是合理的，可以优化模型。并且随着转化率提高，气体扩散将逐渐占据产物层扩散主导。

关键词：模型；直接硫化；石灰石

中图分类号:TM731

文献标识码:A

DOI:10.3969/j.issn.1672-0792.2015.10.012

收稿日期：2015-06-30。

基金项目：中央高校基本科研业务费专项资金(2014QN41)。

作者简介：白子为(1992-)，男，硕士研究生，主要研究方向为热能污染物治理，E-mail：316330392@qq.com。

Abstract：Among the coal-fired pollution control methods, flue gas desulfurization is widely used in view of its low investment costs and easy manipulation. Accordingly, limestone becomes the first choice for the calcium-based sorbent because of its low prices and desulfurization effectiveness. However, there is no consensus on the inner reaction mechanism of the direct vulcanization. Considering this sistuation, a new model of direct vulcanization of limestone is presented in this paper. The new model is based on the Knudsen gas diffusion, sintering and coexistence of the diffusion theories. Experimental data has justified the applicability of the new model. The results show that the hypothese of sintering and coexistence of the diffusion theories are reasonable, which can optimize the data fitting. And the gas diffusion gradually becomes the main part with the arugment of the conversion rate.

Keywords：model；direct vulcanization；limestone

0引言

对于直接硫化模型，已有很多学者进行过研究。如陈传敏等[1，2]通过实验分析了直接硫化中温度、CO2分压和SO2分压的影响，并认为直接硫化可提高Ca转化率，有利于更充分地利用脱硫剂进行烟气处理[3]。刘彦等[4]验证了在富氧和空气气氛下的硫化实验机理和现象存在差异，并对控制因素进行了比较分析。

石灰石的直接硫化反应是气体和固体之间发生的多相反应，反应气氛要求如前文证实为富氧气氛，足够浓度的CO2浓度才能保证石灰石颗粒不会在煅烧期间发生分解反应。直接硫化反应的模型以未反应收缩核模型为较多数认可的选择。未反应收缩核模型假设了反应颗粒在发生硫化反应中存在一个反应界面，该界面随着反应的进行而不断向颗粒核心移动。同时也有部分研究人员支持相似孔隙模型并分析了石灰石在直接硫化中的反应机理。

对于扩散机理，主流的机理学说分别是气体扩散学说和固体扩散学说。气体扩散学说认为在直接硫化中随着反应的进行，是SO2气体分子不断穿过硫化产物层以达到反应界面并与未反应的石灰石发生硫化反应；固体扩散学说认为在CaSO4硫化产物层形成后是其中的Ca2+和O2-等固体离子在不断扩散以维持硫化反应的进行。

对于烧结方面，已有一些学者们通过设计相关实验来测量石灰石颗粒的烧结温度，烧结的温度大约是533 ℃[5]。而这一温度远低于直接硫化实验的设计温度，因此对石灰石直接硫化进行研究时，应对烧结对反应中孔隙率的影响加以修正。姜中孝[6]指出固态离子扩散时易发生结焦。陈传敏等[2]也提出在发生直接硫化反应中应该将烧结影响与煅烧、硫化影响综合考虑才比较合理的观点。

1模型描述及假设

富氧气氛下直接硫化反应的气体气氛以O2及CO2为主，陈传敏等[1]学者分别对气氛中各气体成分对直接硫化的影响进行了实验与分析，证明O2分压超过5%后不再对反应产生影响，所以笔者将不再讨论O2气体成分对石灰石直接硫化的影响。

如图1所示为直接硫化反应的石灰石颗粒示意图。反应开始阶段，由于石灰石小颗粒孔隙率很小，假设认为石灰石颗粒由多个无孔小颗粒组成，在小颗粒上反应气体从表面向内部扩散，并在CaCO3/CaSO4反应界面上发生反应，生成物将从内部扩散到颗粒表面。直接硫化反应发生在石灰石小颗粒上CaCO3和CaSO4的接触面上，随着反应进行反应界面逐渐向颗粒核心移动，未反应核体积逐渐减小，原CaCO3成分逐渐由产物CaSO4代替，直到颗粒全成为CaSO4。

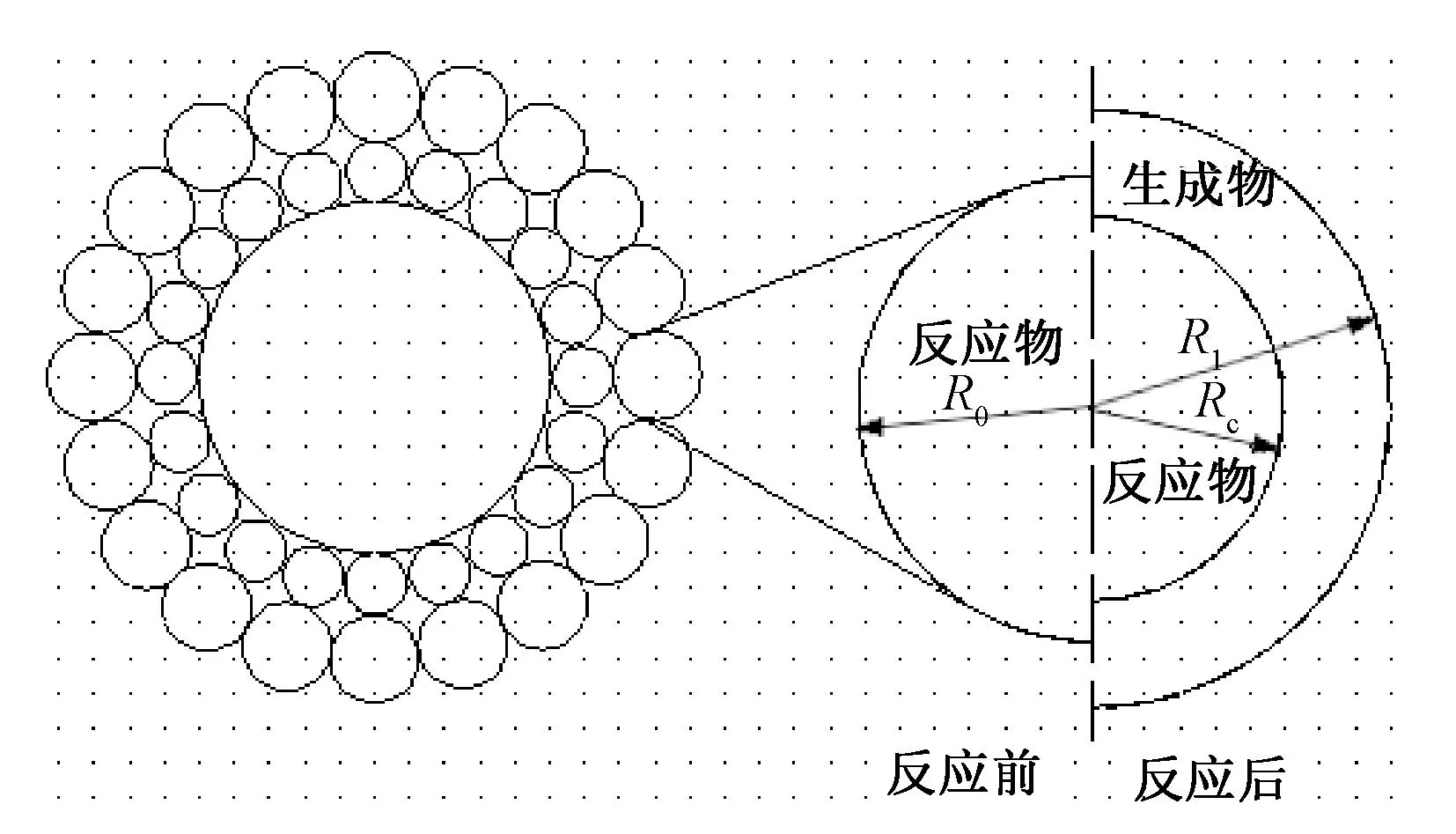
图1　石灰石直接硫化模型颗粒示意图

陈传敏等[2]对直接硫化反应中各时段表观活化能进行了测算，认为随着直接硫化反应的进行，表观活化能存在指数型增长，这一现象的发生表征在反应中的速率影响因素，即控制机理发生了转变，因此推断在直接硫化反应中，应是控制机理存在从开始的化学反应控制向固态离子扩散控制发生的一种自主式转变。王春波[7]通过对电导率的测定和计算也支持认为在钙基脱硫剂硫化反应中存在固态离子扩散。王河山等[8]学者同样认为在硫化反应中，扩散机理应是分阶段的。反应初期，SO2气体分子通过分子扩散形式进入脱硫剂内部并发生硫化反应；在反应后期，产物层覆盖在脱硫剂颗粒表面，气体扩散将转变为离子扩散形式来保障反应的继续进行。

尚建宇[9]学者指出，在反应气体扩散进入反应物颗粒时，气体扩散并非只存在一种扩散机理形式，当孔隙较大时，气体在颗粒孔隙中进行常规扩散，而经典气体扩散系数远大于离子扩散系数；当颗粒的孔隙很小的时候，气体扩散呈现稀薄气体效应，此时经典气体扩散理论将不再适用，于是科学家们将此种气体扩散定义为Knudsen扩散。Knudsen扩散是石灰石发生脱硫反应中普遍存在的一种抑制扩散形式，将使气体扩散能力大幅度降低，离子扩散能力优于Knudsen扩散，颗粒内主要扩散机理发生转变，笔者即假设在此界面从气体扩散为主转换为以离子扩散为主。

Hu[10]认为，在产物层中并非只有单一扩散的存在，应该是气体扩散与固体扩散并存的，对于颗粒核心不同距离处主流扩散方式可能会不同，从而证实了本文所持观点。即在颗粒外表面到转化界面之间的产物层，为以气体扩散为主；在转化界面到反应界面之间的产物层，为以离子扩散为主。

因此，在整个反应模型建立时，可以简化假设反应发生在以下步骤顺序中：

(1)气氛中反应气体从外界扩散吸附到固体小颗粒外表面成为气相传质；

(2)反应气体从颗粒外表面扩散到产物层中并转化为反应物离子；

(3)反应物离子从产物层扩散到颗粒反应界面上；

(4)反应物离子在反应界面发生直接硫化反应，并生成产物离子；

(5)产物离子从反应界面扩散到产物层中并转化为产物气体；

(6)产物气体从产物层扩散到颗粒外表面解吸成气相传质；

(7)产物气体从颗粒外表面扩散入气体气氛。

因假设忽略表面气体扩散阻力，所以认为步骤(1)和(7)与反应参数无关,并且遵循固态离子扩散学说假设要求：常压恒温、O2过量、颗粒为球形且尺寸相近、整个系统在近稳态环境下。

满足假设条件情况下，通过计算求解以下方程来描述直接硫化反应机理并研究反应中的影响因素。

1.1　反应气体在颗粒间径向的扩散方程

由实验假设知石灰石颗粒发生直接硫化反应时处于恒温常压稳定CO2分压的拟稳态环境，所以反应气体中CO2在产物层的浓度应大于抑制石灰石煅烧分解的临界浓度且随反应进行保持稳定。

对于SO2气体在颗粒产物层中的气体扩散过程如下：

浓度近似为稳定状态，不随时间改变：

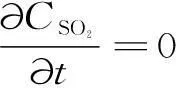
(1)

浓度分布近似均匀稳态：

(2)

并存在边界条件：

R=R1时，

(3)

R=Rw时，

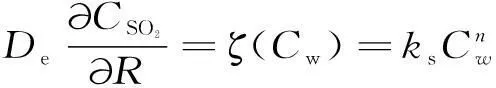
(4)

式中：R1为颗粒开始时外表面到颗粒核心的径向距离，m；Rw为转化界面到颗粒核心的径向距离，m；C0为反应气氛中SO2的摩尔体积常数，kmol/m3；CSO2为SO2在颗粒粒径中径向分布摩尔体积变量kmol/m3；Cw为转化界面上SO2的摩尔体积常数，kmol/m3；De为SO2气体在产物层中的有效扩散系数，cm2/min；ks为硫化反应速率常数，m4·mol-1·s-1；n为SO2在硫化反应中的反应级数；kf为外部传质系数，m/s。

1.2　固体离子扩散的微分方程

固体扩散理论指出，CO32-离子与SO42-离子在CaSO4产物层中相对移动以保证粒子电荷稳定。实验假设反应时间足够长，可为准稳态环境，假设CaCO3离子在产物层中的扩散方程为：

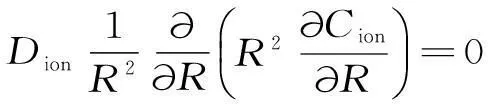
(5)

(6)

边界条件为：

R=Rc时，

(7)

R=Rw时，

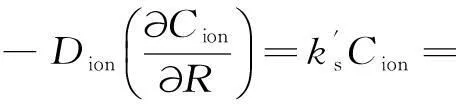
(8)

推导即得

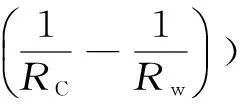
(9)

式中：Dion为离子扩散系数，m2/s；ρCaCO3为CaCO3的摩尔密度，kmol/m3；Rc为反应界面到颗粒中心的距离，m；Cc为反应界面处的SO2气体浓度，kmol/m3。

1.3　反应界面的平衡方程

1.3.1基于固体离子扩散的硫化反应速率rA

Mahuli[11]以CaO-SO2硫化反应为基础建立了以固体离子扩散机理为模型理论的硫化反应速率表达式：

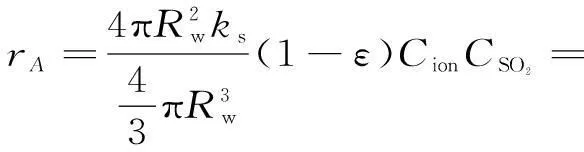
(10)

式中：ε为硫化后局部孔隙率；Cion为硫化产物层钙离子浓度，mol/m3； Rw为CaCO3颗粒气体分子与离子转化界面到颗粒中心距离，m。

硫化后，硫化产物CaSO4的摩尔体积大于反应物CaCO3的摩尔体积，因此随着反应进行，生成产物将堵塞部分孔隙，造成局部孔隙率减小；而Barker[12]实验得石灰石的烧结温度在533 ℃左右，远低于直接硫化反应温度，因此长时间高温的反应环境，石灰石颗粒烧结现象将进一步减小孔隙率。Wang[13]进行过钙基脱硫剂孔隙率的测定与特性推断，在结合前人观点，拟采用下式描述孔隙率变化：

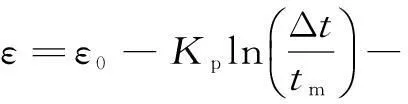
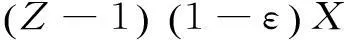
(11)

整理公式(11)得：

(12)

式中：ε0为颗粒硫化前的孔隙率，转化率X由下式求出[12]：

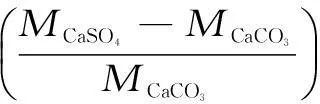
(13)

式中：m为颗粒总质量，g；m0为颗粒初始质量，g；MCaSO4和MCaCO3分别表示CaSO4和CaCO3的分子量。Δt为反应时间，s；tm为烧结弛豫时间，s；Kp为孔隙烧结指数，为受反应温度影响的计算参数，由于对石灰石的烧结研究和实验数据较少，因此借鉴CaO的烧结计算结果并提出修正系数U，孔隙烧结指数Kp最终表达式如下：

Kp=(0.060 67-1.657×10-4T+

(14)

1.3.2 固态反应物消耗速率rB

直接硫化反应中反应颗粒的消耗速率rB可以由反应界面到颗粒中心的距离RC的变化表示：

(15)

并存在边界条件：

t=0时，

(16)

1.3.3 反应界面平衡方程

由于反应颗粒即为消耗颗粒，因此存在关系式rA=rB，代入式(10)和式(15)得：

(17)

整理得：

(18)

上式与公式(9)联立得：

当R=Rw时，

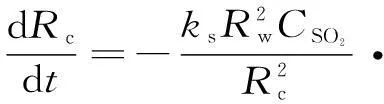
(19)

上式联立公式(16)得：

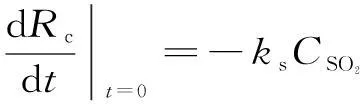
(20)

即反应开始阶段，颗粒表面变化速率与CSO2成一次关系。

1.4　颗粒体积变化关系

由反应界面半径表达反应物与产物体积变化为:

(21)

化简上式得:

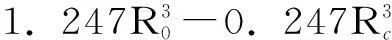
(22)

1.5　转化界面确定

当气体分子逐渐深入颗粒孔隙的过程中，开始时孔隙率和孔容积衰减很快，随后开始减缓，据推测是因为微颗粒上孔隙堵塞迅速而微颗粒间孔隙不易堵塞[9]。伴随着反应的进行，颗粒的平均孔径减小，气体在孔隙中的扩散形式逐渐由常规气体扩散转变为Knudsen气体扩散。尚建宇[14]等学者认为，当气体处于Knudsen气体扩散形式时，伴随稀薄气体效应，连续介质假设和Navier-stokes方程将不再适用，促使SO2浓度在颗粒径向分布梯度增加。

笔者引入中间参数Thiele模数，从而对扩散机理进行假设判定：由尚建宇[9]等学者指出，转化界面处Thiele模数的判定取值为1，转化界面处定义为气体扩散与离子扩散主导作用转变的假设分界面层。在Thiele模数大于1时认为颗粒孔隙间气体适用于常规气体扩散理论；当Thiele模数小于1时气体扩散形式将转化为Knudsen扩散，因此认定在此界面上颗粒内的扩散形式转变为离子扩散起主要作用。

对于转化界面的计算， 尚建宇[9]指出Thiele模数可表示如下：

(23)

式中：φ为Thiele模数，为一无因次数群； CΩ为截面积常数；CS为直径常数；Ω为分形通道截面积；δ为气体分子当量直径；df 为分形维数；Dk为Knudsen扩散系数[9]。

2模型验证

2.1　转化界面计算与验证

在任意时刻转化界面到颗粒核心的距离Rw可由公式(23)推导计算求得如下式：

(24)

转化界面的计算解与公式解绘图表征如图2所示。

图2　转化界面计算图

由图2可以看出，在任意直接硫化时刻，Knudsen扩散判定假设界面值与计算出的转化界面曲线数值相近，曲线变化趋势相同，因此可以得出结论即对于本次实验数据与石灰石直接硫化模型，由Thiele模数确定的转化界面假设的趋势合理，且适用性良好，是与转化界面的最初设计要求相符合，可以用其参与后续的计算。

2.2　实验数据与模型验证

公式(9)为以Ca2+离子为讨论对象进行的方程建立与求解，同理可得当以SO42-离子为研究对象时，在产物层中的以离子扩散为主要扩散方式的扩散方程可以表示如下：

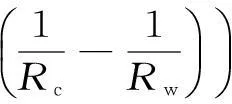
(25)

其中，公式(25)成立范围为在颗粒半径R=Rc到R=Rw之间的以离子扩散为主要控制因素的产物层中。

由公式(24)与公式(25)、公式(9)、公式(22)联立求解，即可在已知石灰石颗粒直接硫化反应中转化率与时间关系的基础上，求得反应界面到石灰石颗粒核心之间距离Rc与时间之间的函数关系曲线，之后再引入公式:

(26)

进行联立即可绘出转化率曲线。

根据在1 023 K温度下的石灰石直接硫化中转化率与时间的实验数据关系，代入本文建立的石灰石直接硫化模型，其中实验气体气氛如表1，可以计算出石灰石直接硫化的转化曲线，实验数据与模型计算数据拟合结果如图3。从图3可以看出，模型对实验数据的拟合结果非常好，实验数据与计算数据相近，这也证明了在模型中对烧结影响的考虑是确实有必要的。

表1　设计实验气体气氛

图3　模型拟合曲线结果

3模型结果与分析

计算数据与实验数据均对转化率随时间的变化显示为上升趋势，即表明石灰石转化率不断增加；并由转化率增长趋势推断随着反应时间的延长，转化率可能继续提高，这一推论与很多学者们的观点相一致。徐红莉[15]认为直接硫化反应中脱硫剂转化率较高。陈传敏等[3]认为在直接硫化反应中CaSO4产物层缺陷程度高于同等条件下的间接硫化产物层的缺陷程度，因此提高了最大转化率，并实验论证温度为1 023 K条件时的最大转化率约为57%。

由计算结果可得出，随着转化率的提高，模型计算数据转化界面处SO2气体浓度Cw基本稳定不变，数值近似稳定为离子浓度上限，计算数值如表2。分析浓度稳定原因可能是转化界面为同时受气体扩散和离子扩散影响的假设界面，该界面受两种界面平衡影响，因此计算结果与实验预期相同。

表2　转化界面浓度

如图4所示，对于本实验，气体扩散适用比例逐渐增加，而离子扩散产物层厚度基本保持不变。Hu[10]在文章中提到了类似的结论，支持了本文观点。

图4　不同扩散形式产物层厚度

4结论

本文根据前人已有的结论和模型公式，总结提出一种新的石灰石直接硫化模型，并完善其理论基础，做出了相对科学的理论假设。通过石灰石直接硫化反应的实验数据代入模型计算验证，从而得出了以下结论：

(1)对随着转化率提高孔隙率和反应界面浓度的变化趋势进行了描述，并提出了合理猜测认为随着转化率的提高，会导致总产物层厚度增加，颗粒外层产物层的孔隙率增加，从而导致总体孔隙率的提高和总体气体扩散阻力的提高。

(2)对实验数据的计算结果进行了分析绘图，描述了产物层中离子扩散和气体扩散的适用范围变化趋势，发现针对于本次实验气体扩散将逐步占据主导因素。

参考文献：

[1]陈传敏, 赵长遂, 韩松, 等. 石灰石直接硫化实验研究[J]. 锅炉技术, 2005, 36(3): 64-67.

[2]陈传敏, 赵长遂, 梁财, 等. 高CO2浓度下石灰石硫化特性实验研究[J]. 燃烧科学与技术, 2006, 12(5): 453-456.

[3]陈传敏, 赵长遂, 赵毅. 石灰石直接硫化反应动力学研究[J]. 燃烧科学与技术, 2009, 15(5): 388-392.

[4]刘彦, 韦宏敏, 齐学义, 等. 在 O2/CO2-空气两种不同气氛下石灰石硫化特性的比较[J]. 动力工程, 2006, 26(2): 267-272.

[5]Wu S F. Beurm T H, Yang J I, et al. Properties of Ca-base CO2sorbent using Ca(OH)2as precursor [J]. Ind. Eng. Chem. Res, 2007, 46(24):7896-7899.

[6]姜中孝, 段伦博, 陈晓平,等. 空气燃烧与O2/CO2燃烧气氛下水蒸气对石灰石煅烧/硫化特性的影响[J]. 中国电机工程学报, 2013, 33(26):14-20.

[7]王春波, 张斌, 陈亮, 等. 富氧燃烧气氛下石灰石煅烧/硫化特性及模型模拟[J]. 化工学报, 2015, 66(4):1537-1543.

[8]王河山, 尚建宇, 王松岭, 等. 钙基脱硫剂硫化反应产物层扩散机理研究进展[J]. 电力科学与工程, 2009, 25(1): 62-65.

[10]Guilin Hu. Kinetics of the direct sulfation of limestone at the initial stage of crystal growth of the solid product[J]. Aiche Journal, 2010, 57(6):1607-1616.

[11]Mahuli S K, Agnihotri R, Jadhav R. Combined calcination, sintering and Sulfation model for CaCO3-SO2reaction[J]. Aiche Journal, 1999,45(2):367-382.

[12]Ronald Barker. The reversibility of the reaction CaCO3=CaO+CO2[J].Journal of Appl. Chem. Biotechnol., 2007, 23(10):733-742.

[13]Wang Chunbo, Zhang Yue, Jia Lufei. Effect of water vapor on the pore structure and sulphation of CaO[J]. Fuel, 2014, 130:60-65.

[14]尚建宇, 王松岭, 王春波. SO2气体在微孔CaO脱硫剂颗粒内的Knudsen扩散[J]. 热能动力工程，2009,24(3):382-385.

[15]徐红莉. O2/CO2燃烧含水蒸汽气氛下石灰石硫化特性的实验研究[D]. 武汉：华中科技大学, 2013.

A Model of Direct Vulcanization of Limestone

Bai Ziwei, Wang Chunbo(School of Energy Power and Mechanical Engineering, North China Electric Power University, Baoding 071003, China)