输电系统N-k故障运行风险分析

梁艺腾，王致杰，王海群

(上海电机学院 电气学院，上海201306)

输电系统N-k故障运行风险分析

梁艺腾，王致杰，王海群

(上海电机学院 电气学院，上海201306)

摘要：随着电网的发展与扩大，N-k故障日益成为造成大规模停电事故的主要原因之一。为研究电网中N-k故障的风险，首先建立考虑多种因素的输电线路可靠性模型和考虑隐性故障的保护系统运行可靠性模型；然后针对传统的系统可靠性评估方法的不足，提出了考虑N-k故障的输电系统风险评估方法，实现系统实时运行情况有效地计算出N-k故障的路径；基于保护元件的隐性故障分析，结合风险理论，建立符合市场要求下的输电系统N-k故障运行风险模型，该模型能有效地结合电网的运行安全性和经济性。最后基于IEEE-RTS79可靠性测试系统进行算例仿真，结果表明，保护配置的方案、输电线率所处运行环境和线路容量都会对N-k故障风险产生相应的影响，基于可靠性理论可以很好地评估输电系统N-k故障运行风险。

关键词：N-k故障；输电系统；隐性故障；风险评估

中图分类号:TM711

文献标识码:A

DOI:10.3969/j.issn.1672-0792.2015.10.011

收稿日期：2015-07-27。

作者简介：梁艺腾(1990-)，男，硕士研究生，研究方向为输电线路N-k故障，E-mail:1028323553@qq.com。

Abstract：With the development of grid, N-k contingency has become one of the main reasons of blackout. To study the risk of N-k contingency, the reliability models of transmission lines considering various factors and hidden fault of protection system were established. In addition, as to the deficiency of traditional reliability assessment method, a risk assessment method of transmission lines considering N-k contingency, which can calculate the real-time N-k contingency paths effectively. Based on hidden fault of protection system and combined with risk theory, N-k contingency operational risk model of transmission system is established according to market condition. Finally, case of simulation was analyzed based on IEEE-RTS79 system. The result shows N-k contingency risk of transmission system can be assessed on the basis of reliability theory.

Keywords：N-k contingency; transmission system; hidden fault; risk assessment

0引言

近年来世界各地不断发生大规模停电事故，这极大地引起了电力系统专家的广泛关注[1～5]。大停电事故一般是由连锁反应导致的故障造成，连锁反应从时间上一般可以划分为3个阶段：慢过程相继开断、快过程相继开断和恢复阶段[6]。大量研究表明，大规模停电事故中，有超过50%的事故存在慢开断过程[7]，即在此过程中，能通过有效措施减缓甚至抑制事故的继续扩大，从而减少经济损失。虽然N-k故障发生概率小，但造成的损失极为严重，有可能带来难以评估的后果[8～9]。因此本文主要针对慢开断过程中的N-k故障进行研究。

目前，针对输电系统N-k故障的研究主要从以下两方面着手：一方面，以复杂网络理论为基础分析输电线路系统拓扑结构对N-k故障的影响，如小世界网络模型[10～11]、无标度网络模型[12]等；另一方面，以复杂系统理论为基础分析电网停电事故中的幂律特性对N-k故障的影响。以上模型很好地对N-k故障发生机理进行了解释，但仍有不足之处，在对输电线路进行开断选择时往往只考虑单一因素对输电线路的影响，即只考虑线路潮流影响或保护系统的隐性故障。因此，如何在系统运行过程中，根据实际的保护配置，考虑不同因素对输电线路的影响，从而跟真实地反映输电线路的开断选择和过程，客观评价N-k故障概率和风险仍需进一步研究。

本文首先建立考虑多种因素的输电线路可靠性模型和考虑隐性故障的保护系统可靠性模型；然后针对传统的系统可靠性评估方法的不足，提出了考虑N-k故障的输电系统风险评估，在N-k故障搜索流程中考虑外界因素的影响，实现系统实时运行情况有效地计算出N-k故障的路径；基于保护元件的隐性故障分析，结合风险理论，建立符合市场要求下的输电系统N-k故障运行风险模型，该模型能有效地结合电网的运行安全性和经济性。最后基于IEEE-RTS79可靠性测试系统，分别对N-k故障的运行风险排序和线路潮流限值对N-k故障风险的影响进行分析，验证了所提方案的其合理性和有效性。

1基于多重不确定因素的输电线路运行可靠性模型

在实际情况中，电力系统的运行工况每时每刻都在发生变化，输电线路的运行情况也在发生改变，影响着输电线路的不确定因素主要有以下几部分[13]：

①输电线路自身因素，如绝缘层老化或损坏。

②输电线路应过载运行导致保护设备的动作。

③输电线路所处的自然天气环境，如大风、冰雪、雷击等。

④保护设备的不正确动作。

第一种和第二种因素是与输电线路本身的运行情况直接相关；第三种因素为基于对输电线路所处的外部天气环境决定，本文仅计及风速对输电线路故障率的影响；第四种因素是由保护设备引发的，为隐性故障。

1.1　基于输电线路自身因素的停运概率模型

传统方法的基本思想是根据以往事故的统计数据获得同类输电线路的故障概率，其计算简便，简单实用。但是缺点十分明显，该方法的实现必须要有足够多的数据作为支撑，一旦缺乏数据，就很难保证所求故障率的精确性。

国家电网在2008年《输变电设备状态检修试验规程》和相关电气设备的运行状态评分导则，引入了设备运行状态评分的概念，制定了一系列对设备进行评分的机制和体系，对设备的运行状态进行定量的计算。现有浙江和河南的检修系统已采用该评分体系。

本文以架空线路为例。输电线路主要由接地装置、杆塔、绝缘子、导地线、金具、基础等部分组成，评分标准如表1所示。如果输电线路的每个单元都在正常状态下运行，那么输电线路的运行状态就评为正常，其分值为各输电线路的各个单元评分之和。如果输电线路的有单元在注意状态、异常状态或严重状态下运行，那么该输电线路的状态由运行状态最差的单元决定，对照运行状况最差的单元所属的运行状态进行评分，所得分值即为输电线路的状态分值。

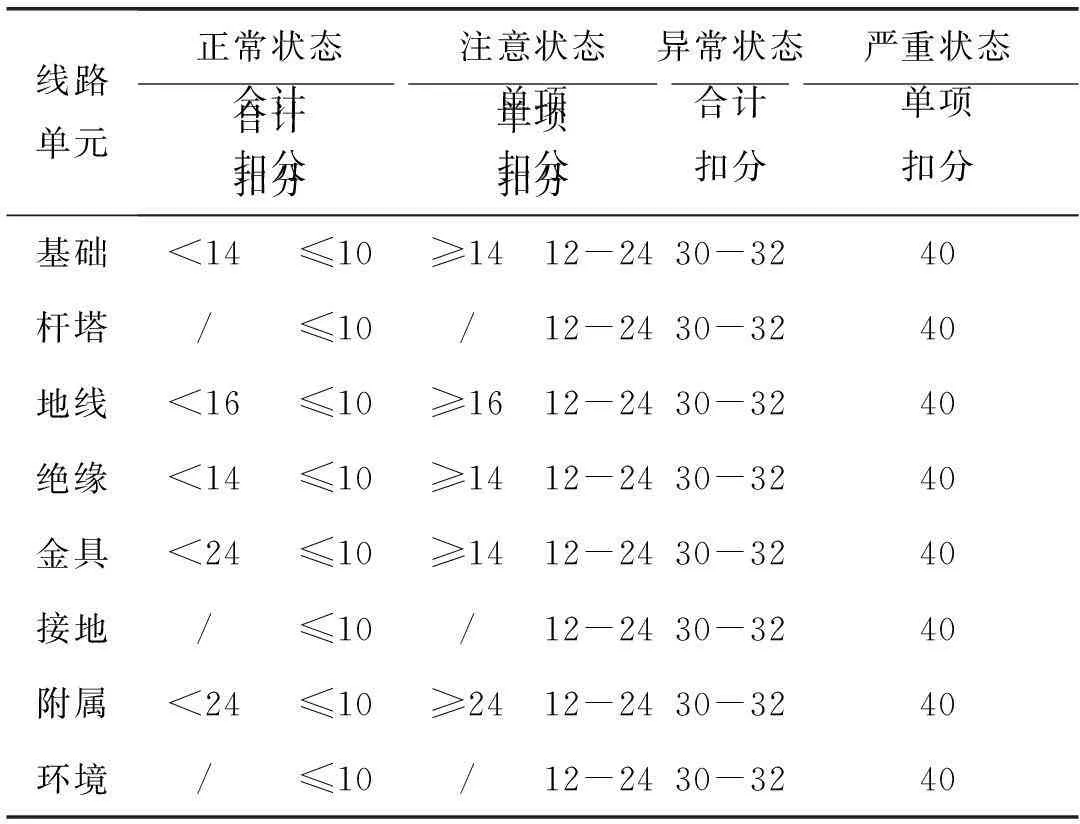
表1　输电线路状态评分标准

基于表1，可以得到输电线路的故障率：

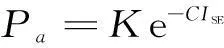
(1)

式中：ISE为输电线路的运行状态评分结果，该值的大小与输电线路的运行状态优劣成正比；K为比例系数；C为曲率系数；Pa为输电线路的故障率。

1.2　基于输电线路运行工况的停运概率模型

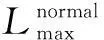
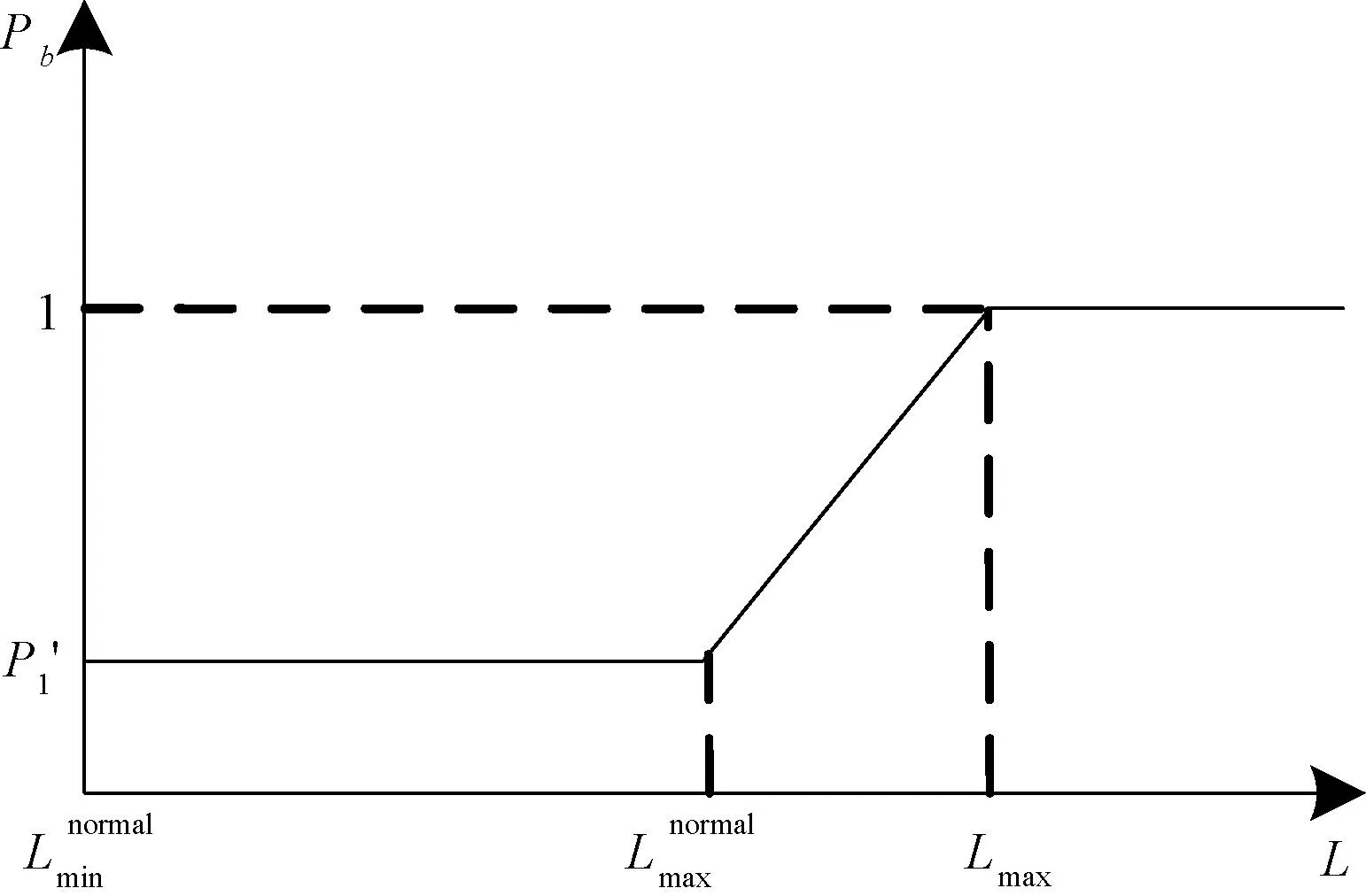
图1　基于潮流变化的输电线路停运模型

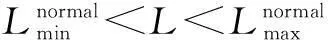
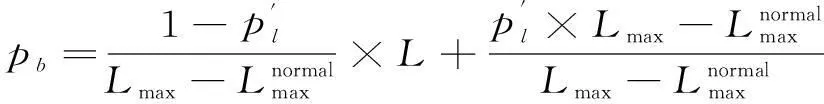
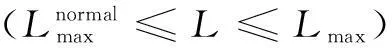
(2)

1.3　基于输电线路所处环境因素的停运概率模型

实际情况中，输电线路是在露天环境下运行的，天气环境因素对线路的运行状态有着一定程度的影响。冰雪、台风、雷雨等一些恶劣的环境会增大线路的故障概率。本文考虑到风速的变化，建立计及风速的输电线路停运概率模型。

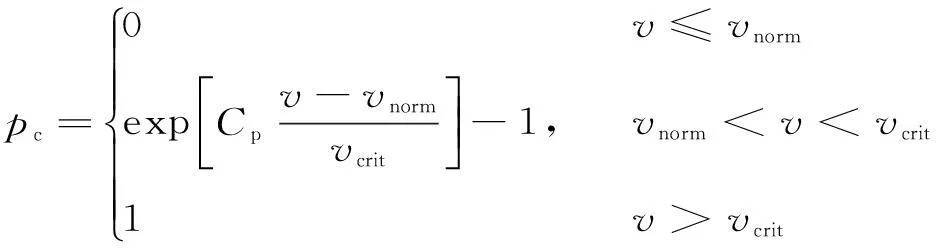
(3)

式中：Cp为尺度参数，Cp≤ln2；vnorm由输电线路的种类决定；vcrit=kvnorm，k为输电线路的重要因数，一般为k=1， 1.1， 1.2，若该输电线路所需的安全级别越高，那k的取值也越大，vcrit的值也越大。

1.4　考虑综合因素的线路停运概率模型

因此，综合以上因素，建立基于自身因素、潮流和外界因素的输电线路停运模型：

Pl=Pa+Pb+Pc-PaPb-PbPc-PaPc+PaPbPc

(4)

2基于状态空间法的继电保护隐性故障概率模型

2.1　状态空间法

状态空间法[15]是一种根据马尔科夫过程而建立的用来分析应用在电力系统中的元件可靠性的方法。在可靠性模型建立中，转移率是一个非常重要的参数，其含义是在一定时间内元件状态a转移到状态b的次数期望。转移率与转移概率的关系如下：

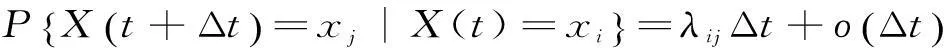
(5)

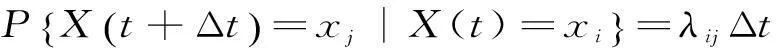
(6)

用状态空间法来分析系统中的元件可靠性，其步骤如下：

①分析系统中元件的状态并对其进行划分，确定每个状态代表的物理含义，即确定保护元件的状态为误动、拒动或是正常工作。

②根据各状态相互之间的转移逻辑构建状态空间图。

③建立方程组并求解。

④计算得出状态概率之后便可求得其他相关可靠性指标。

2.2　隐性故障机理

隐性故障[16]是一种保护元件的永久性缺陷，隐性故障的特点就是在电网正常运行的情况下不会发生，当且仅当系统受到扰动发生故障的时候，保护元件的隐性故障才会被激发，致使被保护元件不正确断开，从而造成故障的蔓延。隐性故障的特点是发生概率小，但是危害严重，其造成的社会影响和经济损失是难以估计的，应当予以足够的重视。

2.3　110 kV电压等级的保护配置方案

影响隐性故障的主要因素就是保护设备的配置差异，保护配置方案又是由输电线路电压等级决定的，因此需要分多个不同的电压等级进行分析，本文主要分析110 kV和220 kV或以输电线路。

在110 kV电压等级输电线路中，通常配置有一套全线速动保护和零序电流Ⅰ段保护。

在对保护系统的可靠性进行建模之前，首先假设：

①保护设备的维修率和故障率保持不变，分别设为常数μ和λ；

②保护设备的故障不在同一时间发生，即故障发生有先后；

③断路器正常工作。

根据马尔科夫理论和保护的配置和动作逻辑，110 kV输电线路保护系统的状态空间转移图如图2所示。

图2中，状态1为输电线路、主保护和后备保护正常工作；若输电线路发生故障则状态2转为状态3；若主保护拒动则状态2转为状态3；若后备保护拒动则状态3转为状态4；若主保护误动则状态1转为状态5；若后备保护误动则状态5转为状态6。

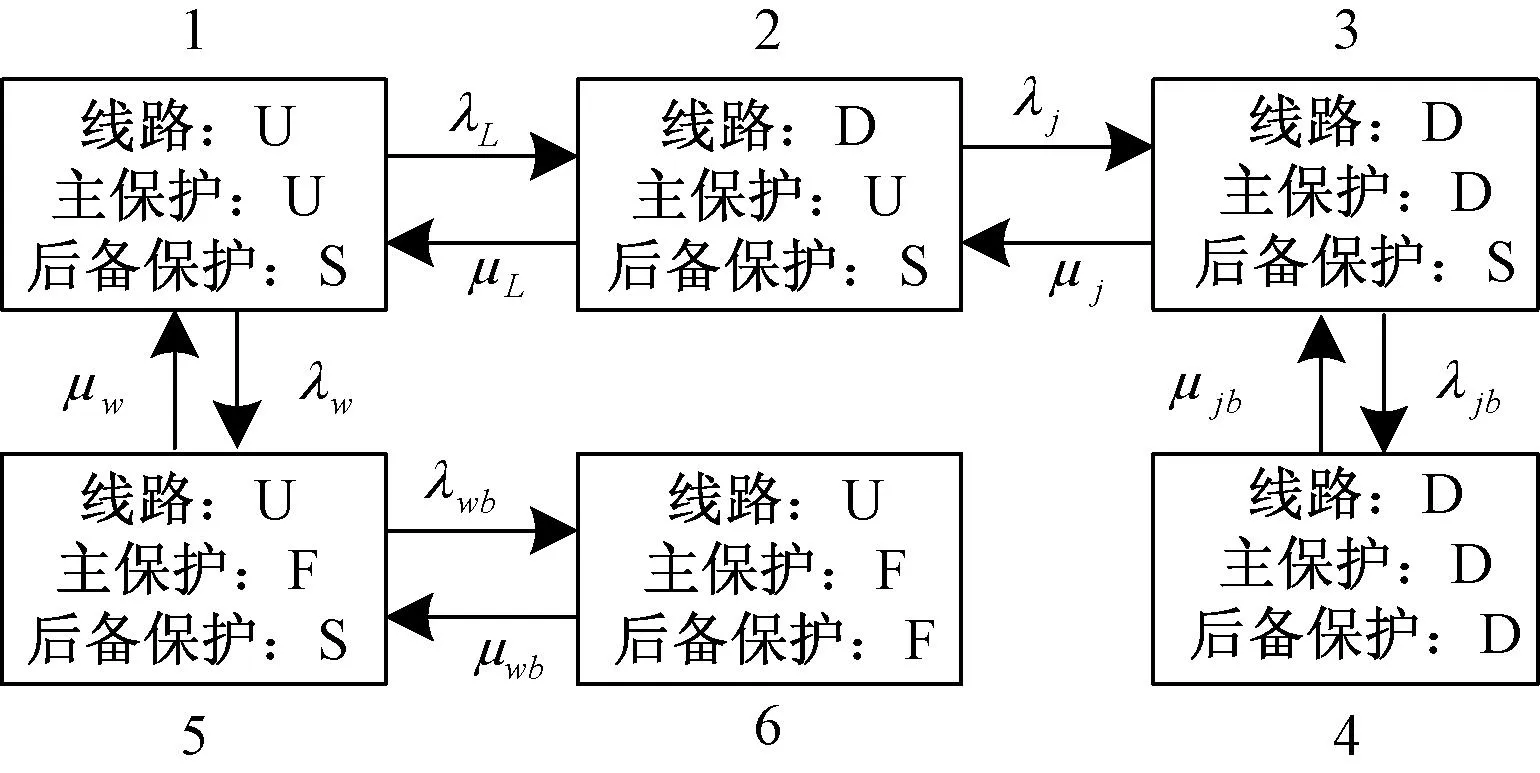
图2　110 kV输电线路保护系统的状态空间转移图

根据马尔科夫理论，其状态方程为

(7)

其中

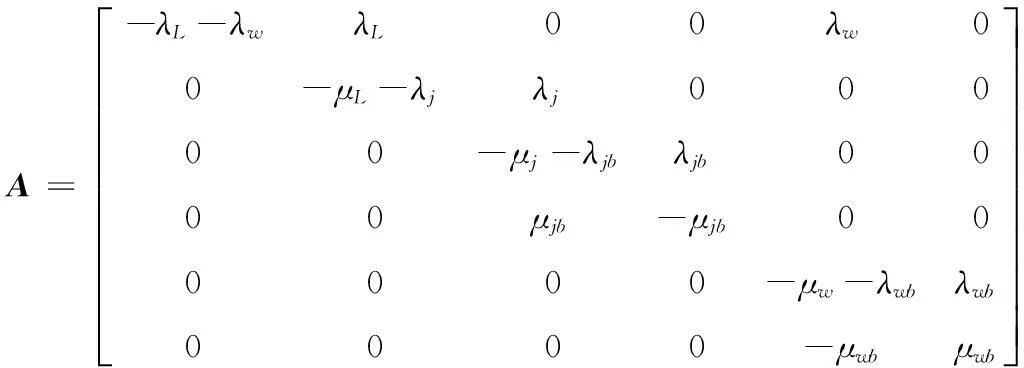
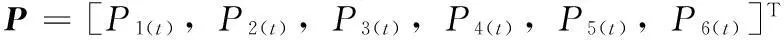
其中：A为状态转移矩阵，即转移概率密度矩阵；Pi(t)为在t时刻保护设备处于状态i的概率。

根据马尔科夫状态逼近原理,可求出系统处在各个状态的概率Pi，保护系统正常运行概率pA、失效概率pU、误动概率Pbw和拒动概率pbj分别为

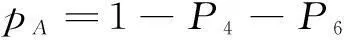
(8)

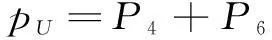
(9)

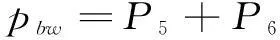
(10)

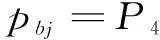
(11)

2.4　220 kV电压等级的保护配置方案

在220 kV或以上的电压等级输电线路中，通常装设两套完整的独立的全线速动保护。

根据马尔科夫理论和保护的配置和动作逻辑，220 kV及以上电压等级输电线路保护系统的状态空间转移图如图3所示。

图3中，状态1为输电线路和两套主保护以及后备保护均处于正常工作状态；若输电线路发生故障则转为状态2；若其中一套主保护发生拒动故障则状态2转为状态3；若另一套主保护也发生拒动故障则状态3转为状态4；若一套后备保护发生拒动故障则状态4转为状态5；若另一套后备保护也发生拒动故障则状态5转为状态6；若其中一套主保护发生误动故障则状态1转为状态7；若另一套主保护也发生误动故障则状态7转为状态8；若一套后备保护发生误动故障则状态8转为状态9；若另一套后备保护也发生误动故障则状态9转为状态10。

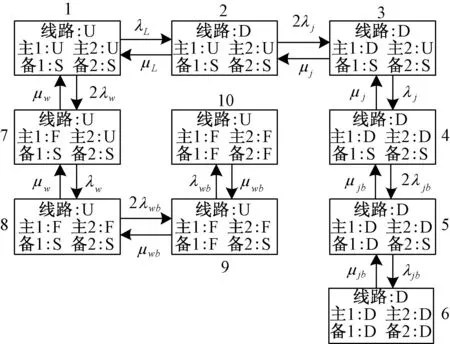
图3　220 kV及以上电压等级输电线路保护系统的状态空间转移图

类似的，根据马尔科夫状态逼近原理,可求出系统处在各个状态的概率Pi，保护系统正常运行概率pA、失效概率pU、误动概率Pbw和拒动概率pbj分别为

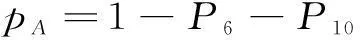
(12)

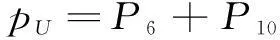
(13)

(14)

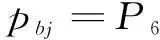
(15)

3基于N-k故障的电力系统运行风险

3.1　电力系统运行风险

基于电力系统的运行风险，其定义为电力系统故障发生概率与事故严重程度的乘积，式(16)为数学表达式。

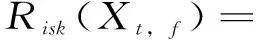
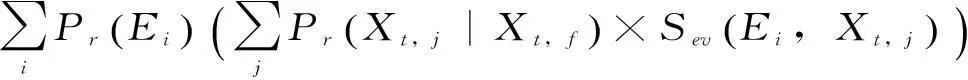
(16)

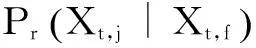
3.2　N-k故障路径搜索

基于输电线路的实时停运概率模型和保护系统的隐性故障概率模型，本文提出N-k故障路径搜索流程：

(1)选择输电线路的起始故障；

(2)重新计算潮流，更新输电线路的停运概率；

(3)判断是否有无风速原因造成线路断开，有，转至第(2)步；无，转至第(4)步；

(4)判断有无潮流越限的输电线路，有，转至第(6)步；无，转至第(5)步；

(5)判断有无潮流接近限值的输电线路，即L/Lmax≥a。 有，转至第(6)步；无，转至第(7)步；

(6)若存在潮流接近限值或越限的输电线路，则称其为过载线路。利用一个随机数与隐性故障的拒动概率作比较，判断是否触发拒动故障。如果触发拒动故障，则切除该条过载线路相邻上一级的所有线路；如果不触发拒动故障，则再次利用一个随机数与线路停运概率作比较，判断该线路是否停运，转至第(2)步；

(7)按照隐性故障模型，选择保护二类误动概率最大的一条输电线路作为下一跳被切除的线路，然后转至第(3)步；

(8)判断是否潮流不收敛，若是，则结束仿真，计算N-k故障风险指标。

3.3　事故严重程度的评价指标

本文主要针对输电侧故障在经济层面上造成的负面影响进行研究并建立评价指标。电网公司N-k故障中切机切负荷，会给其经济上带来一定的损失，经济损失Sgd的表达式如下：

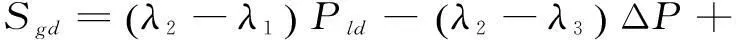
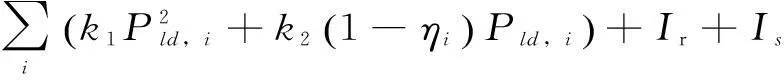
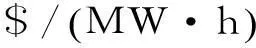
4算例分析

4.1　RTS79系统

以RTS79(Reliability Test System 79)系统为基础，对本文提出的N-k故障进行分析。RTS79系统包括38条线路，24个节点，32台发电机，5台变压器。图4为RTS79测试系统。

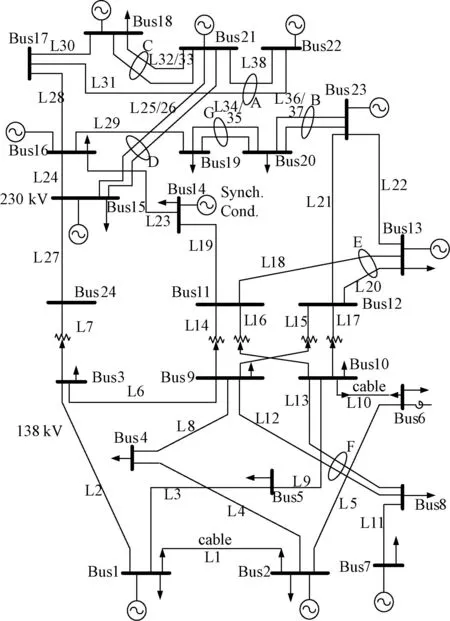
图4　RTS79电气接线图

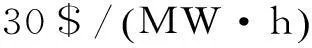
4.2　N-k故障概率分析

根据N-k故障模型可以计算出以不同输电线路的开断作为起始故障的N-k故障概率。分别以38条输电线路的开断作为起始故障，计算相应的N-k故障概率，并进行排序。假设输电线路自身状态为正常。表2为10条造成N-k故障概率最高的输电线路。

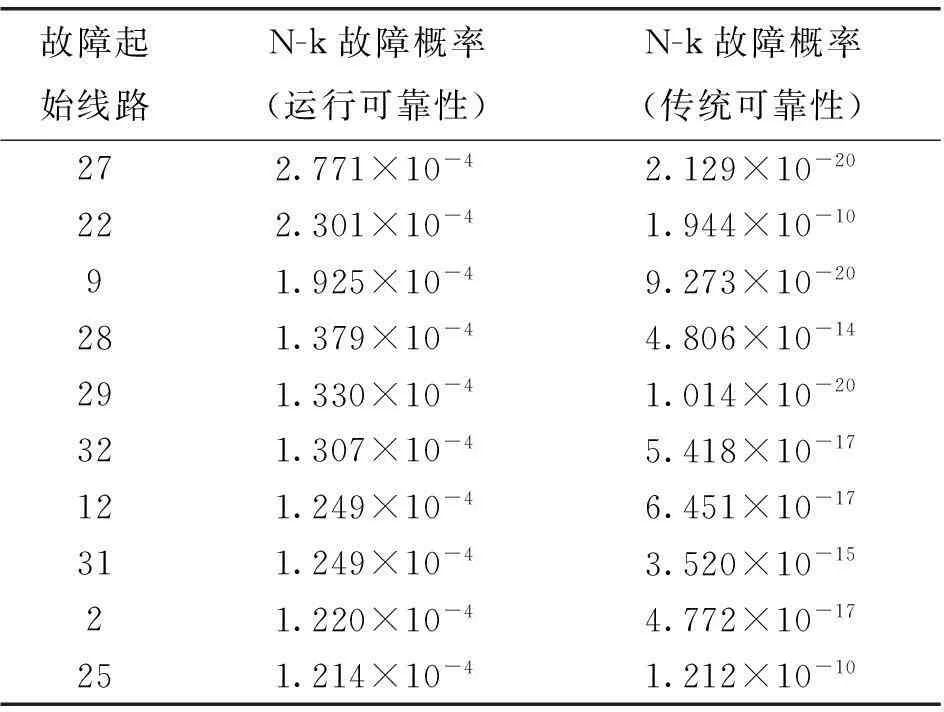
表2　N-k故障概率排序

通过对比不难发现，以运行可靠性模型为基础分析计算得出的N-k故障概率至少比通过传统可靠性计算得出的结果高出6个数量级。其原因在于传统可靠性方法认为元件的开断相互之间是独立的，也就是说一个元件的开断并不会影响到其他元件，N-k故障概率是取每个元件故障概率的平均值的乘积得到的，因此理论上来说N-k故障概率相当低。但在实际的系统运行过程中这类事故近年来时有发生，所以传统可靠性方法不能真实地反映电网实时运行情况下的N-k故障概率。而运行可靠性将输电线路的实时运行工况考虑在内，真实地反映了线路实时变化的故障率，也说明了实际的电网中N-k故障频频出现的原因。

4.3　N-k故障风险值分析

分别以38条输电线路的开断作为起始故障，计算相应的N-k故障风险值，并进行排序。首先假设输电线路自身状态为正常，天气情况良好，即风速小于vnorm，系统输电线率潮流限制设为原先的50%。表3为10条造成N-k故障风险值最高的输电线路。

从表3中可以看出，在10条N-k故障风险最高的输电线路中，230 kV的输电线路占了7条，所以高风险的N-k故障集中于系统上半部分。之所以有这种现象，是因为230 kV输电系统的电源出力接近整个系统的75%，负载也为整个系统的53.3%，在这种情况下，230 kV的输电系统相对于138 kV，其输电线路的负荷较重，运行工况更为恶劣，所以更容易触发N-k故障，相应的增加了N-k故障风险。

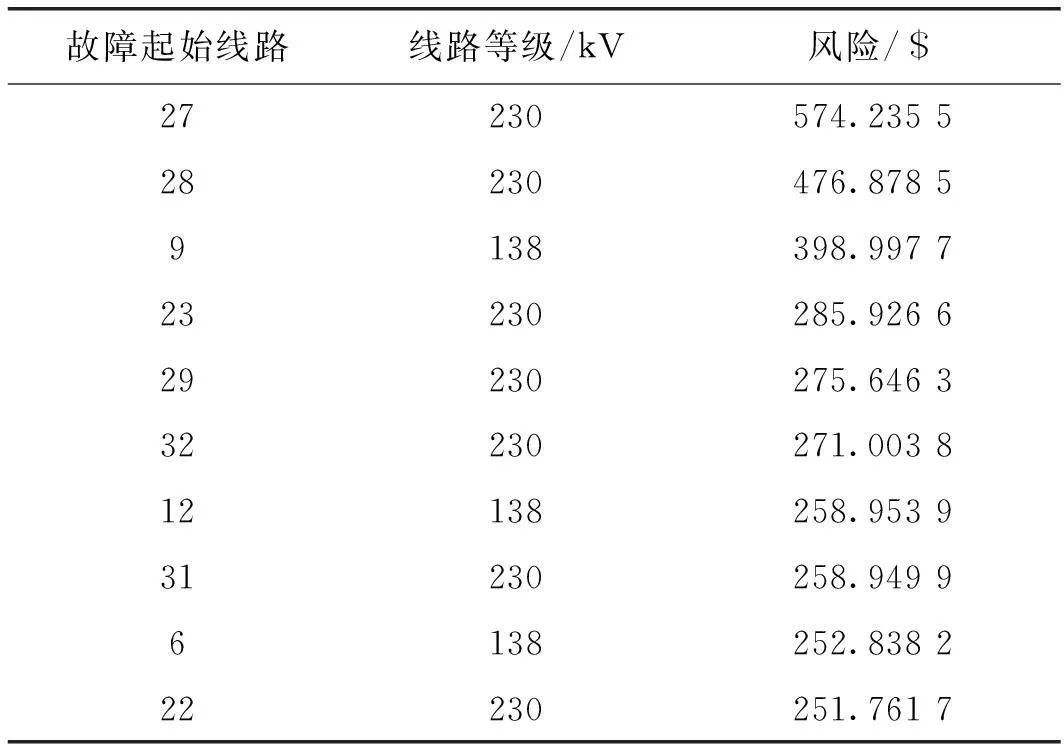
表3　风速为正常情况下的N-k故障风险排序

根据《110 kV～750 kV架空输电线路设计规范》，110 kV电压等级输电线路的vnorm等于23.5 m/s，220 kV及以上电压等级输电线路的vnorm等于27 m/s。所以取风速为25 m/s和28 m/s，再次对N-k故障风险值进行计算并排序，得表4和表5。

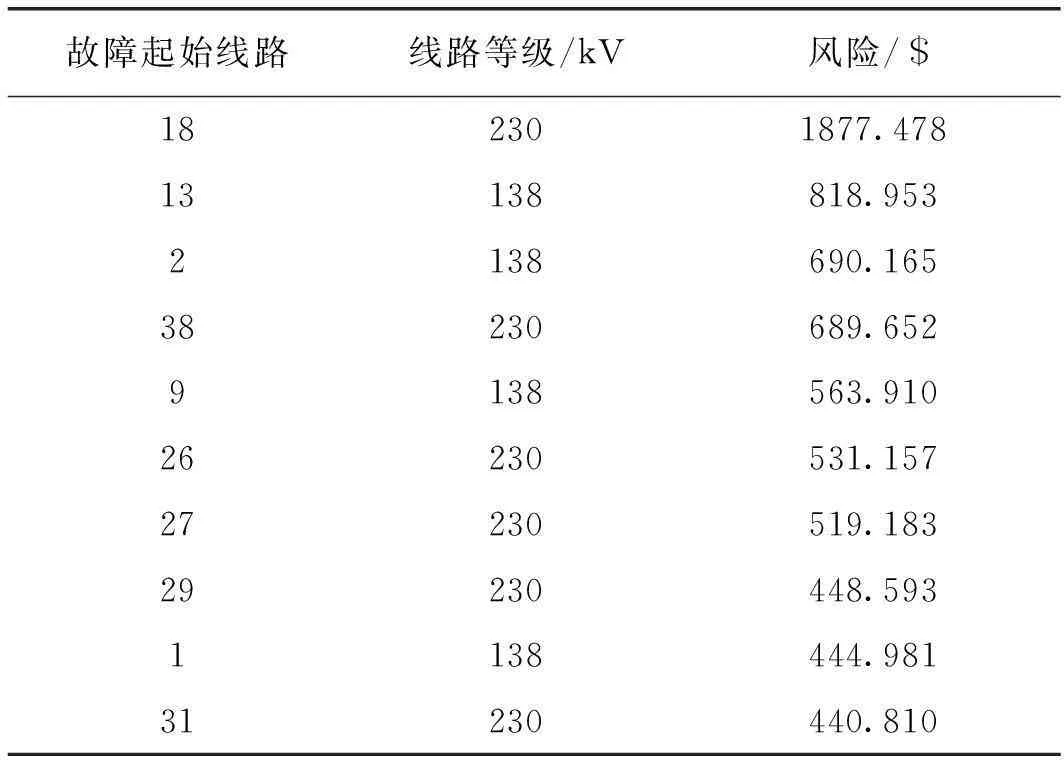
表4　风速为25 m/s情况下的线路风险排序

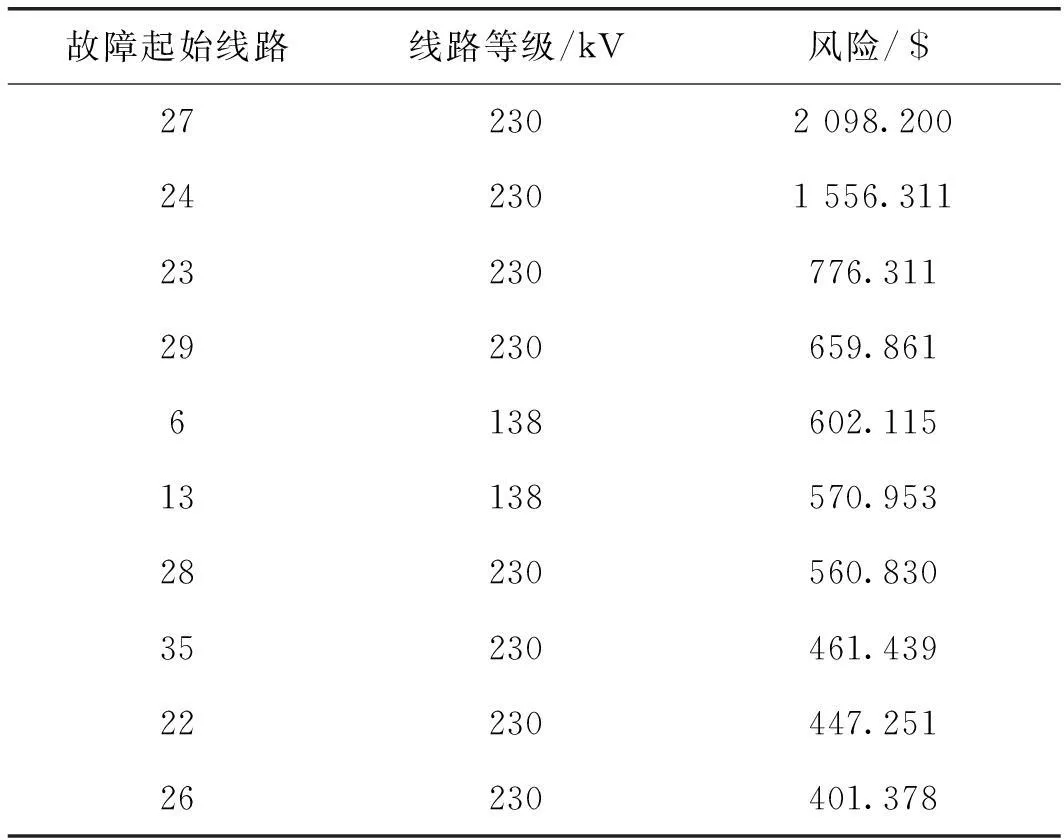
表5　风速为28 m/s情况下的线路风险排序

比对表3、表4和表5，不难发现，当风速处于正常值范围时，N-k故障风险值较低；随着风速的增大，N-k故障风险值也随之显著上升。这说明了该模型可以很好地定量分析风速对输电线路停运概率的影响。其中初始故障线路27和29均出现在表3、表4和表5中，因此在系统运行中需要对这两条线路多加关注并予以及时的维修，以避免造成事故的扩大。

4.4　线路潮流限值对N-k故障风险的影响

为分析线路潮流限值对N-k故障风险的影响，将RTS79系统各输电线路的潮流限值进行下调并计算N-k故障风险值。分别以第27,18和28条输电线路的开断作为起始故障，对不同潮流限值情况下的N-k故障风险值进行计算,结果如图5所示。

图5　线路开断造成的故障风险(不同潮流限值)

根据图5可以看出，随着输电线路的潮流限值的减小，N-k故障风险随之增大。当输电线路的潮流限值介于原先限值的100%～55%时，N-k故障风险在一定范围内波动，基本保持平稳。当输电线路的潮流限值介于55%～40%时，以第18条和第28条输电线路的开断作为起始故障的N-k故障风险略有上升，而以第27条输电线路的开断作为起始故障的N-k故障风险大幅上升。当潮流限值低于40%时，风险均有显著上升趋势，此时很有可能发生大规模停电事故。

从上述风险随潮流限值的变化趋势可以看出，以第27条和第18条输电线路的开断作为起始故障的N-k故障风险要高于另外一条。其原因在于线路27和18都是承载230 kV区域和138 kV区域的关键线路，其负荷较之其他线路相对较重，而且这两条线路中的任意一条开断都会导致系统解列。所以在系统设计以及运行时都要重视这两条线路，出现问题时及时应对，以免发生大规模事故。

所以，线路潮流限值对N-k故障风险有着直接必然的影响，降低风险的有效措施就是增加各输电线路的潮流限值。

5结论

本文首先建立考虑多种因素的输电线路可靠性模型和考虑隐性故障的保护系统可靠性模型；然后针对传统的系统可靠性评估方法的不足，提出了考虑N-k故障的输电系统风险评估方法，实现系统实时运行情况有效地计算出N-k故障的路径；基于保护元件的隐性故障分析，结合风险理论，建立符合市场要求下的输电系统N-k故障运行风险模型，该模型能有效地结合电网的运行安全性和经济性。最后基于IEEE-RTS79可靠性测试系统进行算例仿真，结果表明，保护配置的方案、输电线率所处运行环境和线路容量都会对N-k故障风险产生相应的影响，与传统可靠性相比，基于本文的可靠性理论评估输电系统N-k故障运行风险可以如实反映系统实时运行情况下的可靠性水平，结果合理准确。

参考文献：

[1]En L U, Xiaojun L U, Long F, et al. Indexes and method of power system outage risk assessment [J]. Electric Power Automation Equipment, 2015.

[2]方勇杰. 用紧急控制降低由输电断面开断引发系统崩溃的风险——对印度大停电事故的思考[J]. 电力系统自动化, 2013, 37(4):1-6.

[3]李冬明, 刘磊. 电网大停电的研究[J]. 科学与财富, 2013，(12):250-251.

[4]辛阔, 吴小辰, 和识之. 电网大停电回顾及其警示与对策探讨[J]. 南方电网技术, 2013,7(1):32-38.

[5]Brasca C, Ciapessoni E, Cirio D, et al. Extended risk analysis of power and ICT systems[C]// Innovative Smart Grid Technologies Europe (ISGT EUROPE), 2013 4th IEEE/PESIEEE, 2013:1-5.

[6]肖贤, 周步祥, 刘念,等. 模拟电网连锁故障缓慢开断阶段的相关模型[J]. 电力系统及其自动化学报, 2015, 27(3):76-80.

[7]吴旭. 基于N-k故障的电力系统运行风险及脆弱性评估[D]. 保定：华北电力大学, 2013.

[8]Mousavi O A, Cherkaoui R, Bozorg M. Blackouts risk evaluation by Monte Carlo Simulation regarding cascading outages and system frequency deviation[J]. Electric Power Systems Research, 2012, 89(4):157-164.

[9]李扬, 苏慧玲. N-k故障下影响电力系统脆弱性的关键线路研究[J]. 电力自动化设备, 2015，35(3):60-67.

[10]董光德. 基于潮流介数和UPFC的小世界电网连锁故障模型研究[D]. 重庆：重庆大学, 2013.

[11]Cotilla-Sanchez E, Hines P D H, Barrows C, et al. Comparing the topological and electrical structure of the north american electric power infrastructure[J]. Systems Journal IEEE, 2011, 6(4):616-626.

[12]Zhang Y, Bao Z, Cao Y. Long-term effect of relay protection operation on cascading failures in growing scale-free small-world power grid[C]// Power and Energy Society General Meeting, 2012 IEEE, 2012:1-6.

[13]刘海涛,程林,孙元章,等.基于实时运行条件的元件停运因素分析与停运率建模[J].电力系统自动化,2007,31(7): 6-11

[14]唐玲玲. 基于马尔科夫理论的输电线路可靠性研究[D]. 长沙：湖南大学, 2013.

[15]Han Guangyue. Limit theorems in hidden markov models [J]. Information Theory IEEE Transactions on, 2013,59(3): 1311-1328.

[16]孙光, 陈金富, 陈志光,等. 计及继电保护系统多模式隐藏故障的电网N-k风险分析[J]. 电力系统自动化, 2014, 38(15):37-43.

Analysis on Operational Risk of Transmission System on N-k Contingency

Liang Yiteng, Wang Zhijie, Wang Haiqun(School of Electrical Engineering, Shanghai Dianji University, Shanghai 201306, China)