基于ITAE的时滞过程内模PID滤波器参数优化
2016-01-26冯新强韦根原
冯新强, 韦根原
(华北电力大学 控制与计算机工程学院,河北保定071003)
基于ITAE的时滞过程内模PID滤波器参数优化
冯新强, 韦根原
(华北电力大学 控制与计算机工程学院,河北保定071003)
摘要:针对热工系统中普遍存在的一阶时滞、二阶时滞热工过程,提出以ITAE指标为目标函数,利用黄金分割法对IMC-PID的滤波器参数进行优化。首先,仿真研究了ITAE指标函数对滤波器参数呈单峰性的特点,然后采用黄金分割法对滤波器参数进行快速寻优,从而使系统响应达到最优性能指标。仿真结果表明,该方法能够快速地寻优出滤波器参数,对热工系统的控制研究以及运行操作人员具有一定的指导意义。
关键词:时滞过程;ITAE;IMC-PID;黄金分割法
中图分类号:TM273
文献标识码:A
DOI:10.3969/j.issn.1672-0792.2015.10.008
收稿日期:2015-06-30。
作者简介:冯新强(1989-),男,硕士研究生,主要研究方向为智能优化控制,E-mail:fengxq@126.com。
Abstract:For the prevalent one order-delay plus dead time, second order-delay plus dead time thermal process, this paper proposes a method to ITAE index as an objective function, use the golden section method to optimize the IMC-PID filter parameters. First, simulation of the filter parameters ITAE index shows a single peak characteristics, then the study uses the golden section method for rapid optimization of the filter parameters, allowing the system to achieve optimal performance. Simulation results show that this method can quickly optimize the filter parameters, which may provide guidance for research and operational control of the operator of thermal systems.
Keywords:process with time-delay;ITAE;IMC-PID;golden section method

0引言
PID控制具有结构简单、鲁棒性强、适用范围广、易于操作等特点,因而广泛应用于工业控制过程中[1]。PID控制最为核心的问题是如何整定PID控制器的参数,以达到控制要求。Rivera等人将内模控制的思想引入到PID控制器的设计中[2],并建立了滤波器参数与PID控制器参数的关系,与PID直接整定相比,内模PID仅需整定一个参数,大大减少了参数整定的工作量。然而如何快速确定滤波器参数成为一个重要研究课题。
Kang Liu等人根据求取ISE指标方程的最小和补灵敏度函数的最大值确定滤波器参数[3];Skogestad 提出了SIMC整定规则,即令滤波器时间参数等于过程模型等效滞后时间[4]。随着群体智能理论的发展,文献[5]以ITAE为目标函数利用蚁群算法对内模PID的滤波器参数进行整定。工程实际应用中,常把ITAE作为单输入单输出系统的最好性能指标之一。本文根据ITAE指标对滤波器参数大体上呈单峰性的特点,采用黄金分割法对滤波器参数进行快速寻优。
1内模PID控制器
1.1 一阶时滞过程的内模PID控制器设计
1.2 二阶时滞过程的内模PID控制器设计
由上述两式可知,当滞后环节采用一阶Pade近似时,滤波器参数λ只会对比例带δ产生影响,两者呈线性关系。
2目标函数
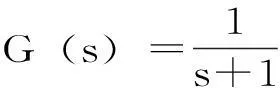

图1 ITAE随δ变化1

图2 ITAE随δ变化2
由前文可知,无论是一阶时滞过程还是二阶时滞过程,其滤波器参数λ与比例带δ都线性相关,所以ITAE指标对滤波器参数λ也呈单峰性。

3黄金分割法
黄金分割法又称“0.618法”,是一维搜索方法中的经典算法,其算法简单、效果显著,是许多优化算法的基础。但它只适用于一维区间上的“非多峰”。其基本思想是:依照对称原则、“去坏留好”原则和等比收缩原则来逐步缩小搜索的范围。具体步骤为:先在区间[a,b]中取两点x1=a+0.382(b-a),x2=a+0.618(b-a),如果f(x1)>f(x2),令a=x1;如果f(x1) 4仿真研究 根据前文先确定Ti,Td的值: (1)由SMIC法可得,λ1=τ=0.5; (2)根据IMC-MAC法:因0.25τ=0.25×0.5=0.125,0.2T=0.2,故λ2=max(0.25τ,0.2T)=0.2; (3)根据前文可知目标函数关于滤波器参数λ成单峰性。故可以利用黄金分割法对λ进行寻优。参照上述两种方法整定的结果,将λ的寻优区域设置为(0.1,10),将黄金分割法的寻优精度设置为E=0.01,寻优结果可得λ3=0.638 7。 由图3可知,根据IMC-MAC法整定出的PID参数,其对应的比例带δ太小,导致输出剧烈波动,控制效果很差。而本文方法和SMIC法整定出结果都可以接受,但由本文方法对应的系统输出,超调量较小、调节时间较短。 图3 FOPTD过程对比 图4 SOPTD过程对比 (1)由SMIC法可得,λ1=τ=1; (3)将λ的寻优区域设置为(0,10),将黄金分割法的寻优精度设置为E=0.01,寻优结果可得λ3=2.242 3。 由图4可知,由SMIC法整定出的PID参数,调节时间过长,控制效果较差。而本文方法整定出的PID参数与IMC-MAC法整定出的参数相比,被控系统响应的超调量较小、调节时间较短。 5结论 仿真研究表明,SIMC法和IMC-MAC法都有一定的适用范围。在两种整定规则适用范围难以确定的情况下,可以根据本文提出的方法快速有效地优化出滤波器参数。以ITAE指标为目标函数采用黄金分割法对滤波器参数进行快速寻优,使系统响应达到最优性能指标。从而为IMC-PID的滤波器参数整定提供了一种新方法。 参考文献: [1]焦嵩鸣,谭雨林,桑士杰. 基于改进粒子群算法的主汽温控制系统PID参数优化[J]. 电力科学与工程,2012,28(12):9-13. [2]王松,张金环,王晓燕,等. 基于分数阶IMC-PID的锅炉蒸汽温度控制[J]. 华北电力大学学报(自然科学版),2014,41(3):70-75. [3]Liu K,Shimizu T,Inagaki M, et al. New tuning method for IMC Controler[J]. Journal of Chemical Engineering of Japan, 1998,31(3):320-324. [4]Skogestad S. Simple analytic rules for model reduction and PID controller tuning [J]. Process Control, 2003, 13(4): 291-309. [5]王浩坤,尚群立. 一阶时滞对象的最优内模PID控制[J].机电工程,2008,25(1):14-17. [6]杨巍. 基于内模整定的PID算法应用与研究[D].北京:华北电力大学,2010. [7]项国波. ITAE最佳控制[M].北京:机械工业出版社,1986.213-248. [8]刘国莉,叶同,王伟.弹性需求下易变质物品定价、营销与生产计划的联合优化[J]. 控制与决策,2015,30(2):361-365. [9]赵志诚,文新宇.内模控制及其应用[M].北京:电子工业出版社,2012.24-27. Internal Model Control PID Optimization for Process with Time-delay Based on ITAE Index Feng Xinqiang,Wei Genyuan(School of Control and Computer Engineering,North China Electric Power University, Baoding 071003,China)4.1 一阶时滞过程
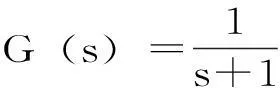

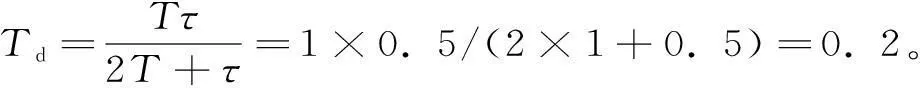
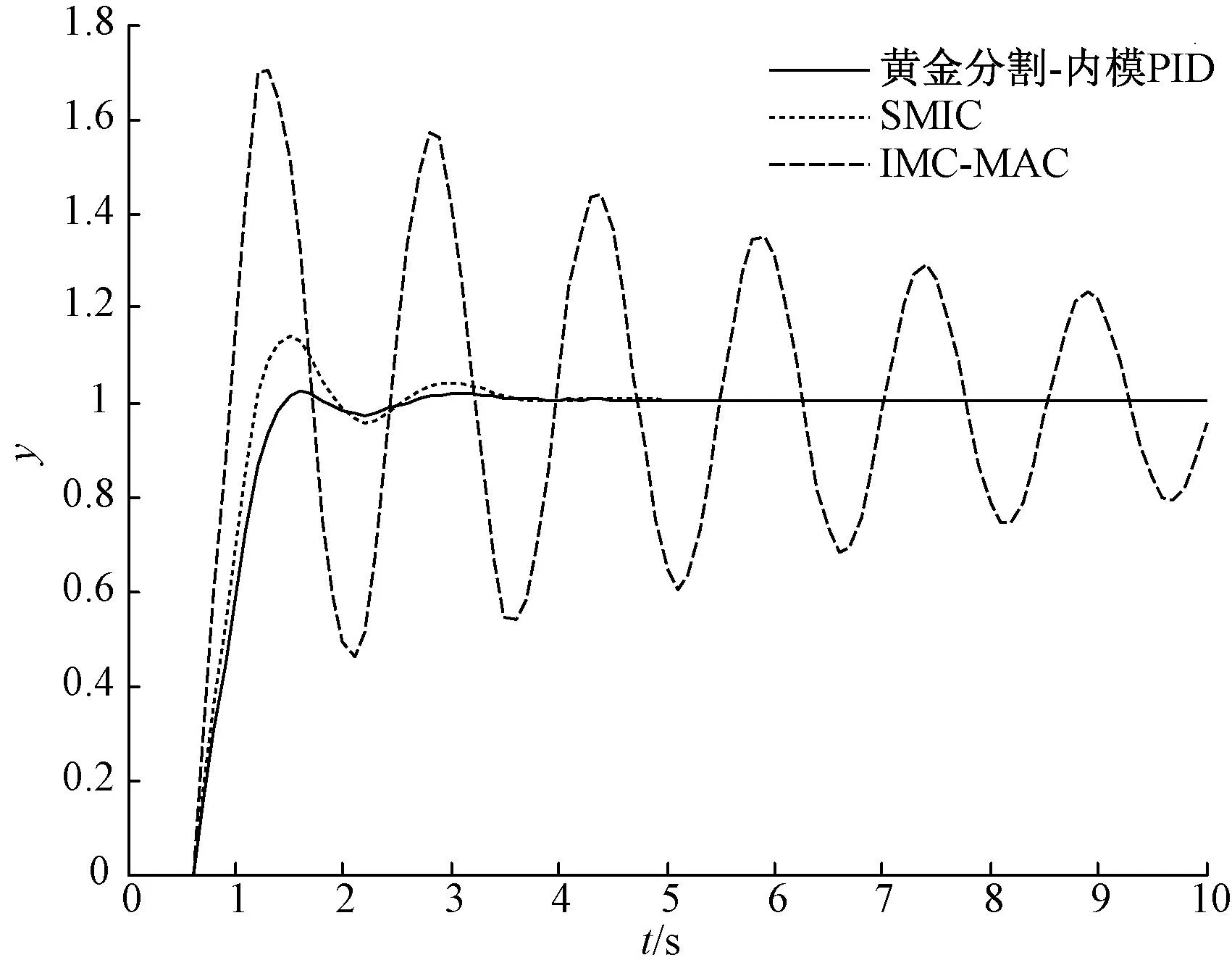
4.2 二阶时滞过程


