基于四元数的三维坐标变换解析解的改进

吕志鹏，伍吉仓，2

(1. 同济大学测绘与地理信息学院，上海 200092；

2. 现代工程测量国家测绘地理信息局重点实验室，上海 200092)

Improvement of Three-dimensional Coordinate Transformation Analytic

Solution Based on Quaternion

LV Zhipeng，WU Jicang



基于四元数的三维坐标变换解析解的改进

吕志鹏1，伍吉仓1，2

(1. 同济大学测绘与地理信息学院，上海 200092；

2. 现代工程测量国家测绘地理信息局重点实验室，上海 200092)

Improvement of Three-dimensional Coordinate Transformation Analytic

Solution Based on Quaternion

LV Zhipeng，WU Jicang

摘要：利用单位四元数构造三维坐标变换最小二乘解析解的过程，具有非迭代、稳定性强等特征。然而，它并不适用于左右手坐标系之间的变换。本文在已有的基于四元数的三维坐标变换解析算法基础上进行改进，使其适合于左右手坐标系之间的变换。同时，利用实际工程案例对其有效性进行了验证。

关键词：三维坐标变换;解析法;单位四元数;左右手坐标系

一、引言

在工程测量、摄影测量、机器视觉等领域，经常需要进行大旋转角三维坐标变换。目前，大旋转角三维坐标变换的解法分为两类：迭代法[1-3]和解析法[4-9]。其中，迭代法将旋转矩阵分别构造为正交矩阵形式[1]、单位四元数形式[2]和欧拉角形式[3]，然后建立牛顿迭代格式求解三维坐标变换参数。解析法采用分布最优的策略，首先求解尺度参数，然后分别利用SVD分解法[4-5]、正交矩阵法[6]、单位四元数法[7-8]对旋转矩阵进行求解，最终获得平移参数。特别地，对偶四元数法[9]可以对旋转矩阵和平移参数进行同步求解。与迭代法相比，解析法不需要初值，计算效率高，对退化点集的鲁棒性好。但是，解析法中的单位四元数法并不适合于左右手坐标系之间的变换，这极大地限制了它在工程测量等领域的应用。为此，本文首先分析了造成这种情况的原因，并提出了解决方案。

二、算法原理

Horn B K P于1987年提出了应用单位四元数构造三维坐标变换解析解的算法[8]。下面对其原理进行简介。对于一组对应点集{pi}和{qi}，i=1,2,…,N。构造三维坐标变换模型

qi=T+kRpi

(1)

式中，T为平移参数；k为尺度参数；R为旋转矩阵。为了计算参数最优解将点集{pi}变换到点集{qi}，需要建立如下目标方程

(2)

将对应点集{pi}和{qi}进行中心化，有

(3)

(4)

将式(3)代入目标方程式(2)并整理得

(5)

考虑到式(4)，可知式(5)中第2项为零。因而，式(5)保留了第1项和第3项。由于此时仅第3项含有平移向量T并且第3项非负。为了让式(5)取得最小值，可先令第3项为零对目标方程进行分步最优化，即

(6)

此时目标方程简化为

(7)

为使对应点集正逆变换保持对称性[7-8]，可将目标方程式(7)改写成对称形式，有

(8)

将式(8)展开得

(9)

式(9)中第1项和第3项含有尺度参数k，此时令它们之和为零，得

(10)

至此，为了让目标方程取得最小值，有

(11)

对式(11)进行变形，得

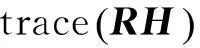
(12)

两个坐标系之间的定向关系，包括旋转变换和左右手指向变换。因而，将同时描述这两种变换关系的矩阵称为定向矩阵。

当对应点集仅存在旋转变换时，式(12)的最大值为矩阵N的最大正特征值，最大正特征值所对应的特征向量就是最优旋转矩阵所对应的单位四元数[8]。设其为q=[q0q1q2q3]，可构造如下旋转矩阵

(13)

如图1所示，给出了左右手坐标系的关系示意图。在仅考虑两个坐标系之间左右手指向的变换时，可得定向矩阵

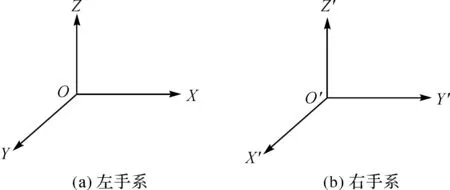
图1　左右手坐标系关系

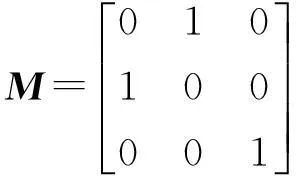
(14)

将式(14)代入式(12)，得式(11)的变型

(15)

因此，当对应点集存在左右手指向变换时，式(15)的最大值为矩阵N的最小负特征值，最小负特征值所对应的特征向量就是最优旋转矩阵所对应的单位四元数。然后，根据式(13)求得旋转矩阵。同时，结合式(15)可知，最终得到定向矩阵

O=-R

(16)

三、实例分析

本文采用文献[1]中广州新机场航站楼网架中一个构件的节点坐标数据进行改进算法验证。在这个实例中目标坐标系(设计坐标系)轴的指向为：X向北、Z向东、Y向上，原点为构件端点铰的中心。原坐标系(测量坐标系)轴的指向为：x向北、y向东、z向上，原点任意假设。因此，两个坐标系之间存在左右手指向的变换。采用本文改进的算法，17个公共点全部参加三维坐标变换的计算，得到尺度因子为u=1.002 031 772 2，平移参数为(ΔX,ΔY,ΔZ)=(-109 110.884,-101 335.296,-96 497.345)，旋转矩阵为

单位权中误差σ0=8.16 mm。同时，采用将文献[1]中的条件方程转换为伪观测方程的方法并利用其数学模型计算三维坐标变换参数。

利用本文改进的算法和文献[1]中的算法完成三维坐标变换并将实测的坐标转换为设计坐标，与已知设计坐标的较差见表1。

表1　转换后的坐标较差　mm

从表1中可知，利用本文算法计算的X、Y、Z方向的坐标较差与文献[1]中的算法计算的坐标较差互差绝大部分都保持在3 mm以内，说明两种算法具有很好的一致性；同时，两种算法计算的坐标较差结果也主要集中在10 mm以内，反映出两种算法对数据均具有很好的拟合。可以说，本文所作的算法改进适用于左右手坐标系变换。

四、结束语

在工程测量、摄影测量、机器视觉等领域需要进行大旋转角的三维坐标变换。基于四元数的三维坐标变换的解析解法能够非迭代、稳定地求解大旋转角三维坐标变换问题。然而，现有算法并不适合于左右手坐标系之间的变换，本文对其进行了改进。同时，利用工程案例对改进算法作了验证，证明了改进算法的有效性，表明其具有实际应用性。

参考文献：

[1]陈义, 沈云中, 刘大杰. 适合于大旋转角的三维基准转换的一种简洁模型[J]. 武汉大学学报：信息科学版, 2004, 29(12): 1101-1105.

[2]赵双明, 郭秋燕, 罗研, 等. 基于四元数的三维空间相似变换解算[J]. 武汉大学学报：信息科学版, 2009, 34(10): 1214-1217.

[3]姚宜斌, 黄承猛, 李程春, 等. 一种适用于大角度的三维坐标转换参数求解算法[J]. 武汉大学学报：信息科学版, 2012, 37(3): 253-256.

[4]ARUN K S, HUANG T S, BLOSTEIN S D. Least-squares Fitting of Two 3-D Point Sets[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1987, 9(5): 698-700.

[5]UMEYAMA S. Least-squares Estimation of Transformation Parameters between Two Point Patterns[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1991, 13(4): 376-380.

[6]HORN B K P, HILDEN H M, NEGAHDARIPOUR S. Closed-form Solution of Absolute Orientation Using Orthonormal Matrices[J]. Journal of the Optical Society of America A, 1988, 5(7): 1127-1135.

[7]HORN B K P. Closed-form Solution of Absolute Orientation Using Unit Quaternions[J]. Journal of the Optical Society of America A, 1987, 4(4): 629-642.

[8]SHEN Y Z, CHEN Y, ZHENG D H. A Quaternion-based Geodetic Datum Transformation Algorithm[J]. Journal of Geodesy, 2006, 80(5): 233-239.

[9]WALKER M W, SHAO L, VOLZ R A. Estimating 3-D Location Parameters Using Dual Number Quaternions[J]. CVGIP: Image Understanding, 1991, 54(3): 358-367.

[10]LORUSSO A, EGGERT D W, FISHER R B. A Comparison of Four Algorithms for Estimating 3-D Rigid Transformations[C]∥Proceedings of the 1995 British Conference on Machine Vision. UK: BMVA Press Surrey, 1995: 237-246.

[11]谭骏祥, 李少达, 杨容浩. 基于非迭代与迭代法联合估计的七参数坐标转换方法研究[J]. 大地测量与地球动力学, 2014, 34(1): 131-134, 138.

引文格式： 吕志鹏，伍吉仓. 基于四元数的三维坐标变换解析解的改进[J].测绘通报，2015(6)：9-11.DOI:10.13474/j.cnki.11-2246.2015.0166

作者简介：吕志鹏(1988—)，男，硕士，助理工程师，主要研究方向为精密工程测量与变形监测。E-mail：lvzhipeng2007@gmail.com

基金项目：中美国际合作项目(2010DFB20190)；国家自然科学基金(41074019)

收稿日期：2014-06-17

中图分类号：P226.3

文献标识码：B

文章编号：0494-0911(2015)06-0009-03