任意厚度梁的动力与稳定解析解

高荣誉，　王德才，　范家让

(1.安徽建筑大学 土木工程学院，安徽 合肥　230601；2.合肥工业大学 建筑与艺术学院，安徽 合肥 230009；

3.合肥工业大学 土木与水利工程学院，安徽 合肥 230009)



任意厚度梁的动力与稳定解析解

高荣誉1，王德才2，范家让3

(1.安徽建筑大学 土木工程学院，安徽 合肥230601；2.合肥工业大学 建筑与艺术学院，安徽 合肥 230009；

3.合肥工业大学 土木与水利工程学院，安徽 合肥 230009)

摘要：通常对于静力、动力与稳定问题的叠层梁仅能得到近似解。本文基于弹性力学的基本方程和状态空间理论，抛弃任何有关应力和位移模式的假定，导出梁的状态方程，得出状态方程变量级数表达式。采用Cayley-Hamilton定理，有效处理静力、动力和稳定问题，得出在任意荷载作用下任意高度叠层梁的封闭解析解。算例结果与有限元解对比，计算高效精确。

关键词：转换层；宽扁梁；高层结构；框支剪力墙；弹塑性。

0Introduction

The problems of plane stress and plane strain are two classical ones in elasticity. A simple beam underplane stress was discussed in Xu (1992) and Timoshenko(1970). They adopted displacement method, stress method and stress function method, respectively. In their discussion the higher-order partial differential equations must be solved. Especially for laminated construction many unknowns must be solved, and these should be great many difficulty. In traditional elasticity, the mechanical quantities are expressed frequently in the form of polynomials. But we have proved that the true exact solution of elasticity cannot be a polynomial in coordinate variable(Fan and Ye, 1990). If the mechanical quantities are adopted in the form of polynomials, then incompatibility among the fundamental equations must appear in the deductive process. Vlasov (1957) proposed the method of initial function (MIF) to analyze problems of thick plates and shells. Bahar (1975) and Rao et al. (1977) introduced the state space and matrix method to the MIF. For an isotropic body the solutions of the initial functions can be obtained a closed form by using Caley-Hamilton theorem. But the closed form is only theoretical one since the solution of initial function has to be expressed in the form of a Meclaurin series. Taking several terms of the series, all the mechanical quantities, in fact, appear to be polynomials of coordinate variable. Adopting the displacement method of elasticity, Srinivas et al[7,8]. (1969, 1970) analyzed the simply supported laminates of isotropic or orthotropic layers. However, the number of calculation might be too great. Moreover, the number of the simultaneous equations will increase sharply as the number of layers increases. Usually, 6pequations should be established, wherepis the number of layers. All the disadvantages in above mentioned references were overcomed by Fan and Ye l[3,9](1990,1993).

Exact analytical solution is given forp-plied beams with arbitrary height, and precision of any desired order can be obtained. All the fundamental equations of elasticity can be exactly satisfied. No matter how many layers are considered, the calculation always leads to solve a set of linear algebraic equations in two unknowns. Since the eigen-equation has no repeated root for orthotropic body, the solution of state equation can be expressed in the exact closed form by using Caley-Hamilton theorem. However, it is certain that repeated root will appear for isotropic body. The exponential function of matrix must use another approach to be expressed in the finite closed form. We have not seen the problem of buckling in elasticity [1,2]. Although the expression of the buckling problem was discussed in strength of material, only longitudinal elastic modulus was considered.Isotropic body has two elastic constants not one, and in the present study longitudinal elastic modulus and Poisson ratio were adopted to solve the buckling problem.

1formulation and solution of the state equation for a simple beam

1.1　formulation of the state equation

A simple beam under plane stress is shown inFig.1. We adopt the symbols and fundamental equations as follows (Xu,1992):

Equilibrium equations are

(1)

In fact, Eqn.1 is the equilibrium equation for beam dynamics andρ to be the density of the material.

Physical equations are

(2)

Inserting geometrical equation inXu (1992) into above figure gives

(3)

Now eliminateσxfrom Eqn. 1 and Eqn.3. From the first figure of Eqn.3 one has

(4)

Inserting the above expression into the first figure of Eqn. 1 yields

(5)

From the second figure of Eqn. 1 can find

(6)

Substitution of Eqn. 4 into the secondfigure of Eqn. 3, one has

(7)

The third figure of Eqn. 3 gives

(8)

(9)

After U and Y are found, the eliminated σxcan be determined from Eqn. 4.

From Eqn. 9 we can prove that each mechanical quantity cannot be a polynomial in coordinate variable y. IfXandVwere polynomials of degreelfor variable y, from the first and the second lines of Eqn. 9UandYwould have to be polynomials of degreel+1. If this is the case, observing the other two figures of the same equation,XandVwould be polynomials of degreel+2 in y, which contradict what has been supposed. However in traditional elasticity the mechanical quantities are expressed in the form of polynomials of some coordinate variables. The errors which occur in these theories are theoretical ones and cannot be controlled. Because of this, there is a limitation of height in solved problem.

Asimple beam as shown in Fig.1, the boundary conditions are

(10)

Selecting

(11)

We see, from Eqn.4 that the boundary condition of Eqn. 10 is satisfied. Substituting Eqn. 11 into Eqn. 9 yields state equation for each m.

(12)

where

(13)

1.2　The exact solutions for statics, dynamics and buckling problems

The solution for state equation Eqn. 12 [Leonard,1996; Fan, 1996][10,11]is

(14)

Let

(15)

(16)

Then Eqn. 14 becomes

(17)

Wheny=h, one has

(18)

D(y) in Eqn. 17 is called the state transfer matrix. R(0) are called initial values, which are two stresses and two displacements at the top surface.

Statics：In statics we should selectωm=0 in Eqn. 13. If at the top surface of a beam (Fig.1) is loaded by uniformly distributed normal pressureq. Expandingqin the form of the following series, one has

where

(19)

In fact, the above expression is four algebraic equation containing four unknowns Um(0)，Vm(0)，Um(h)，Vm(h). Selecting the second and the third lines after simple calculation, one has

(20)

From above equation we can solveUm(0) andVm(0), then the initial values R(0) are known. After finding initial values, for arbitrary y from Eqn. 17 we can find R(y)，These denote that Um(y), Ym(y), Xm(y) and Vm(y) are found. Substituting these quantities into Eqn. 11 respectively, the exact value of every mechanical quantity can be determined. It is explained that since cut off a series, some error will bring about. However the kind of error here is only one of calculation and can be controlled. As we know, there is nothing absolutely exact in the world. Even for a circle, we can not exactly calculate its area becauseπis a series too. Therefore, what is most important is not error, but the control of error. The traditional theories of elasticity are based on various simplifying assumptions, which only satisfy a part of the fundamental equations. The errors which occur in these theories are theoretical ones, and cannot be controlled. This sets great limitation to the thickness of solved problems.

Dynamics：In the calculation of nature frequencies, letqm=0 in Eqn. 20 yields

(21)

At this timeωm≠0 in Eqn. 13. Nontrivial solution of Eqn. 21 gives

(22)

It should be mentioned that instead of being a polynomial inω2as in the ordinary theories, Eqn. 22 is a transcendental one. In fact, Eqn. 22 is the exact frequency equation for each m. It has an infinite number of roots corresponding to an infinite number of frequencies, which can be determined by using the procedure for finding the zero points of a function.

Buckling: If the normal pressurepxacting on the two ends of a beam, the equilibrium equations are

(23)

(24)

(25)

The element of above determinant has two subscripts, corresponding to line and column respectively for element of four-order matrixG(h). Eqn. 25 is the exact buckling equation, for each m it has an infinite number of roots corresponding to an infinite number of critical stresses (the different form of buckling). However the minimal critical stress has the most practical value.

2The exact solution for the statics, dynamics and buckling of laminated beams with two simply supported edges

A beam is composed of p-layers with isotropic materials as shown in Fig. 2(a), in which jth layer is amplified and shown in Fig. 2 (b). In fact Fig. 2 (b) is same with Fig. 1. Repeating the process of Eqn. 17 arrived gives

(26)

where

(27)

Lety=hjin Eqn. 26 yields

(28)

Dj(hj) is a (4×4) constant matrix, which is different for apart layer. In fact, the above expression denotes that the mechanical quantities of the top surface and the bottom surface for thejth layer are linked up by matrixDj(hj). Eqn. 28 is suitable to arbitrary layer, and especially forj=1, 2 gives respectively.

(29)

(30)

R1(h1) is four mechanical quantities of the bottom surface for 1st layer, and R2(0) is four mechanical quantities of the top surface for 2nd layer. At the interface, the continuity condition for the displacement and stresses can be written as

Considering the above expression, substituting Eqn. 29 into Eqn. 30 yields

Using the recurrence figure, the mechanical quantities of the top and bottom surfaces for the whole laminated beam can be written as

(31)

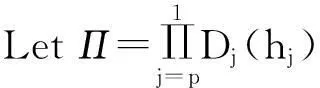
(32)

Then Eqn. 31 becomes

(33)

In whichR1(0) is called initial values, ∏ is a (4×4) constant matrix. Writing the above figure in the evident form gives

(34)

Usually,XmandYmof the top and bottom surfaces should be priori. Therefore, the above equations are a set of linear algebraic equations with four displacements for the top and bottom surfaces of laminated beam. If a uniformly distributed normal pressureqacts at the top surface of the beam, selecting the 2ndand 3rdline a new system of equations is obtained as follows

(35)

From Eqn. 35 findingUm(0) andVm(0) initial values can be determined. Substitution of initial values into Eqn. 26 and letj=1 the mechanical quantities of the 1st layer can be solved. The mechanical quantities found at the bottom surface of the 1stlayer can be taken for the initial values of the 2nd layer. Thus, the mechanical quantities in the 2nd layer can be found. In the same way the whole laminated beam can be solved. In the calculations of natural frequencies and buckling, let right hand of Eqn. 35 equals zero. The nontrivial solution gives

(36)

It should be mentioned that, in the buckling analysis, it is usually presumed the laminated beam is under a state of uniform strain before buckling occurs. This can be achieved for thehomogeneous beam when the normal pressurepxdistribute uniformly over the edges. However, in the case of laminated beam in which the materials are inhomogeneous across the height, if the uniform strainεxis still assumed this means(sxpx)j=A，Where the constantAkeep unchanged for every layer, i.e. the value of the quantity in bracket is independent for the layer. This means thatpxis uniformly distributed on the edges of each layer, but then are sectional uniform across the total height.

3Numerical Examples

A simply supportedsandwich beam with isotropic materials is considered. At its unit width of the top surface is loaded by a uniformly distributed normal pressureq. L and h are span and height of the beam respectively. The top and bottom layers of the beam are identical,μ=0.25 for each layer, butE(1)=E(3)= 5E(2),h1=h3=0.1h,h2=0.8h, density ratioρ(1)=5ρ(2). Some results in Table 1 and 2 are given in comparison with FEM by using ANSYS. For the statics (ω=0)m=1, 3, 5, …, 29

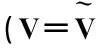
Table 1　Displacement and stress of the sandwich beam qh/E(2), qh/E(2))

Symbols “+” and “-” locked on coordinate denote the outer and interior layers, respectively.

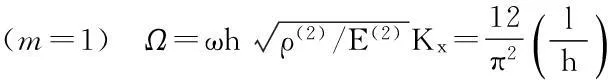
Table 2　The first three natural frequency parameters Ω and the critical stress parameters Kx

4Conclusions

Exact analytical solution of statics, dynamics and buckling problems for laminated beams is achieved using the method of state space. The continuous conditions of stresses and displacements between plies of the laminates are satisfied, and two individual constants of isotropic body are used to express the figure of solving critical loads.

The principle and method suggested here have clear physical meaning and overcome the contradictions and limitations arising fromincompatibility among the fundamental equations in various theories of beam. The present study satisfies the continuity conditions of stresses and displacements at the interfaces which the FEM cannot accomplish. Calculation always leads to solve a set of linear algebraic equations in two unknowns.

Reference

1Xu Z. L.. Applied elasticity. New Delhi:Wiley Eastern Limited, 1992

2Timoshenko S. P. , Goodier J. N.. Theory of Elasticity. Auckland :McGraw-Hill, 1970.

3Fan J. R., Ye J. Q..An exact solution for the statics and dynamics of laminated thick plates with orthotropics layers. International Journal of Solids and Structures, 1990, 26(5-6): 655-662.

4Vlasov V. Z..The Method of Initial Functions in Problems of the Theory of Thick Plates and Shells. 9th Cong. Appl. Mech., Brussels, Belgium, 1957, 6(1):321-330.

5Bahar L. Y. A State Space Approach to Elasticity. J. Franklin I., 1975,229(1): 33-41.

6Rao N. S. V. K., Das Y. C.. A Mixed Method in Elasticity. J. Appl. Mech., 1977, 44(1): 51-56.

7Srinivas S., Rao A. K. .Flexure of Simply Supported Thick Homogeneous and Laminated Rectangular Plates. J. Appl. Math. Mec.,1969,49(8), 449-458.

8Srinivas S., Rao A. K.. Bending, vibration and buckling of simply supported thick orthotropic rectangular plates and laminates. Int. J. Solids Struc.,1970,6(11):1463-1481.

9Fan J. R., Ye J. Q.. Exact solutions of buckling for simply supported thick laminates. Composite Structures,1993,24(1): 23-28.

10Fan J. R.. Exact Theory of Laminated Thick Plates and Shells. Beijing:Science Press, 1996.

11Leonard I. E.. The Matrix Exponential. SIAM Review, 1996,36(3):507-512.

Exact Analytical Solution for Laminated Beams with Arbitrary Height

GAO Rongyu1， WANG Decai2， FAN Jiarang3

(1. School of Civil Engineering, Anhui Jianzhu University, Hefei 230601, China；

2. College of Architecture and Art, Hefei University of Technology, Hefei 230009, China；

3. School of Civil Engineering, Hefei University of Technology, Hefei 230009, China)

Abstract:The approximate solution usually can only be obtained on solving the problem of statics, dynamics and buckling of laminated beams with arbitrary height. Based on the theory of elasticity and the method of state space, the state equation for isotropic laminated beam with simply supported edges is established without any assumptions about displacement models and stress distributions. Series expansion was carried out on the variables of the state equation. Using Caley-Hamilton theory, the exact closed analytical solutions are presented for statics, dynamics and buckling of laminated beams with arbitrary height. The method of calculating critical loads is improved in present. Numerical results of the example are obtained and compared with finite element method. The results show that the convergent solution can be achieved with high accuracy.

Key words:state-space; laminated beam; arbitrary height; exact analytical solution

中图分类号：TU411.01

文献标识码：A

文章编号：2095-8382(2015)02-007-07

DOI：10.11921/j.issn.2095-8382.20150202

作者简介：高荣誉(1964-),男,教授，主要研究方向为高层大跨度结构理论。

收稿日期：2014-09-24