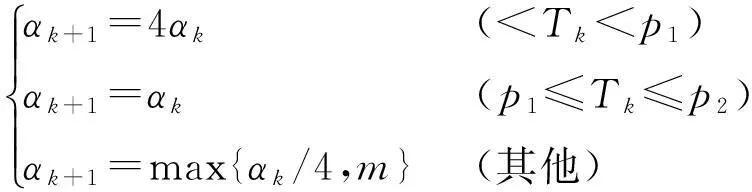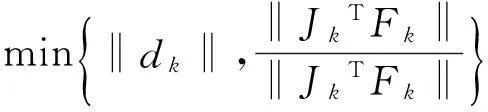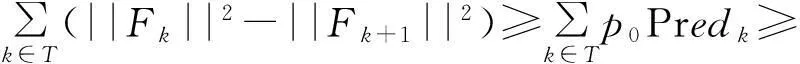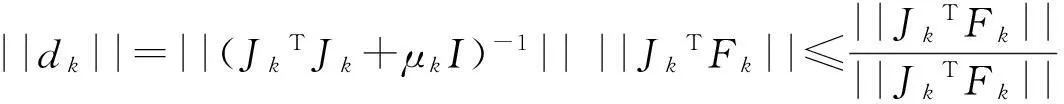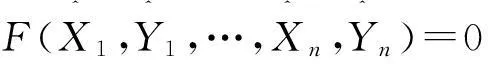全局收敛L-M迭代法的非线性参数平差
2016-01-25王利朋刘成龙
王利朋,刘成龙
(1.西南交通大学 地球科学与环境工程学院,四川 成都 611756;
2.西南交通大学 高速铁路运营安全空间信息技术国家地方联合工程实验室,四川 成都 611756)
全局收敛L-M迭代法的非线性参数平差
王利朋1,2,刘成龙1,2
(1.西南交通大学 地球科学与环境工程学院,四川 成都 611756;
2.西南交通大学 高速铁路运营安全空间信息技术国家地方联合工程实验室,四川 成都 611756)
摘要:采用全局收敛的L-M非线性迭代算法,可以较大程度减弱非线性模型线性化的模型误差,在雅可比矩阵近似奇异或坏条件时,L-M迭代仍然可以收敛;同时,该算法具有全局收敛特性,大大降低了平差对迭代初值的要求,可以在初值受误差影响较大的情况下得到精确解。通过与几种不同的非线性规划算法的比较,证明了全局收敛的L-M迭代算法无论是解算精度还是收敛范围均具有相对优势。
关键词:全局收敛;L-M迭代;非线性参数平差;模型误差

间接平差的函数模型既有线性的,也有非线性的。针对不同类型的函数模型,众多学者和研究人员提出了不同的平差方法,实践证明,相关的数据处理方法均是行之有效的。常见的平差方法包括:经典的最小二乘解法(Least Squares,简称LS);线性化后的牛顿迭代法[1];非线性整体最小二乘(Nonlinear Total Least Squares,简称NTLS)[2];非线性模型的高斯-牛顿(Gauss-Newton,简称G-N)迭代法[3]等。经典最小二乘解法的实质是,对非线性的观测方程进行线性化,按照泰勒展开公式在参数的近似值处展开并保留一次项,从而得到线性化之后的模型,再利用线性最小二乘法(Linear Least Squares)解算。但是,LS参数的近似值必须充分接近其真实值,否则会产生无法忽略的模型误差(Modal Error),对最终的结果产生严重影响。邓兴升等[1]将线性化与牛顿迭代结合在一起,虽然通过牛顿迭代可以以较高的精度收敛,但其前提是函数模型应为线性模型或非线性程度很弱,同时对参数初值的选取依赖性较强,当初值选取接近真实值时,可以线性收敛甚至二次收敛,但牛顿迭代法仍然是局部收敛的,即参数初值选取偏差较大时,无法收敛至真值。胡川等[2]提出的NTLS算法降低了对参数初值的要求并提高了解算的精度。吴玲等[3]提出了非线性模型的G-N迭代法,该方法不需要对非线性函数进行线性化,避免了模型误差,选取适当的初值即可,但仍然存在收敛区间较窄的缺点。无论是经典的最小二乘解法、线性化后的牛顿迭代法或G-N迭代法,对初值的选取都比较敏感,其处理效率及解算结果的好坏都强烈依赖于所选取的初值。为了解决这个问题,本文将一种全局收敛的莱文伯格-马夸特(Globally Convergent Levenberg-Marquardt)迭代算法应用于平差,简称GCLM。该方法由Levenberg提出,并由Marquardt重新发现[5-6]。本文将该方法应用于平差,引入依靠信赖域技巧而不断变化的参数αk,并以此来确定迭代参数μk,确保迭代能够正常进行,解决了G-N迭代中Jk矩阵(第k次迭代的Jacobi矩阵)几乎奇异或坏条件时迭代不收敛的问题。通过实验数据证明,相对于经典的最小二乘法和文献[1]~[3]中的方法,GCLM迭代法具有解算精度较高和收敛范围更大的特点。
1GCLM迭代算法
设非线性方程组为:
F(x)=0
(1)
为了求解该方程组,利用以下线性方程组的迭代解dk来确定真实解的搜索方向,对近似解xk进行纠正:
(JkTJk+μkI)dk=-JkTFk
(2)
式(2)中,k为迭代次数;Jk为第k次迭代的Jacobi矩阵;dk为迭代解的修正值;I为单位矩阵;μk为正则化参数,可以保证JkTJk+μkI对称正定,即式(2)的解dk是适定的。

在G-N迭代法中,要求JkTJk始终保持列满秩,这就限制了该方法的适用范围,当Jk矩阵几乎奇异或坏条件时,给G-N迭代法中的牛顿步带来困难,下式为牛顿步:
dkN=-Jk-1Fk
(3)
dkN为G-N迭代法中的修正值,当Jk坏条件或几乎奇异时,dk会变得很大,影响迭代解的准确性。式(2)中引入非负迭代参数μk,即使JkTJk处于坏条件状态,仍然可以保证JkTJk+μkI具有较小的条件数,可以避免牛顿步中Jk几乎奇异或坏条件时产生的问题,μk可以按照以下公式计算:
μk=αk(θ‖Fk‖+(1-θ)‖JkTFk‖),θ∈(0,1)
(4)
式(4)中:αk可以依据信赖域技巧不断修正[7],||Fk||代表该向量的2-范数。于是可以得到第k步迭代的实际下降量Aredk和预估下降量Predk:

(5)
设置参数Tk=Aredk/Predk,以Tk来探测近似解xk和参数αk,根据Tk的大小确定是否对xk和参数αk进行修正。GCLM迭代算法步骤如下:
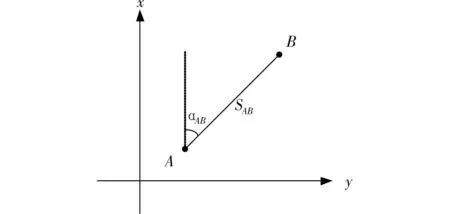
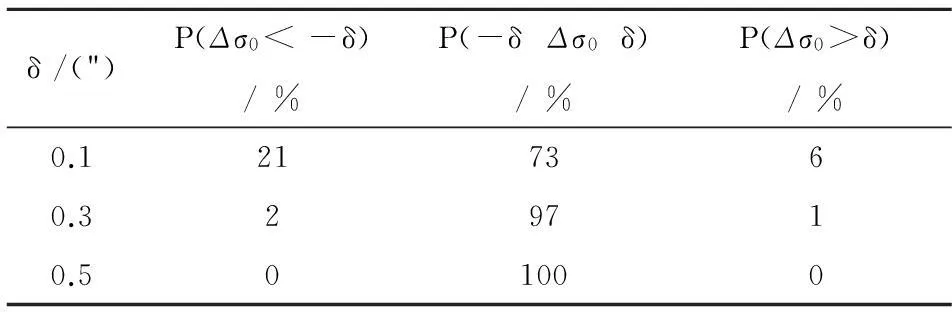
1)设定,x1∈Rn,ε>0,α1>m>0,0 2)判断,如果‖JkTFk‖≤ε,停止计算;否则,依次计算式(4)和(2),得到修正值dk,并执行第3步、第4步和第5步; 3)计算,按照式(5)计算实际下降量Aredk和预估下降量Predk,得到参数Tk; 4)修正, (6) (7) 5)迭代,k=k+1,转第2步(2)。 该算法由于引入了正则化参数μk而保证了迭代的顺利进行,同时具有全局收敛的优势,其解算结果不依赖于迭代初值的选取,下面对GCLM算法的全局收敛特性进行简述。 2GCLM的全局收敛特性 设文献[4]中的假定成立,则GCLM算法经过有限次迭代后会终止,或k次迭代后满足 (8) 此时,若算法(8)迭代不收敛,则存在常数τ> 0,使得无数个k满足 ‖JkTFk‖≥τ (9) 设K与T分别为指标集:K={k||JkTFk||≥τ},T={k|xk+1≠xk,k∈K},由上述GCLM算法可知,当k≥1时 Predk=‖Fk‖2-‖Fk+Jkdk‖2≥ (10) 从而 (11) 同样由上述GCLM算法可知 (12) 根据式(11)与(12)可知 (13) (14) αk→+ (15) 由式(9)和(14)以及(10)可得 (16) 因此,由GCLM算法中αk的取值可知存在常数M>m,使得当k充分大时有 αk (17) 式(15)与式(17)矛盾,从而GCLM算法全局收敛得到验证。 GCLM算法不仅具有全局收敛的特性,同时避免了非线性问题线性化时产生的模型误差,其不依赖于迭代初值的特点使得GCLM算法具有较高的解算精度,下文对GCLM算法的应用以及实例计算的数据进行分析和讨论。 3算例 为了验证GCLM算法的实用性及有效性,以边角网平差为例,简述该算法应用于边角网平差的原理,下文的数据分析选择一个边角观测的单三角形为例按照不同的方法进行平差。如图1所示为边角网中的一条边,SAB为观测边,αAB为方位角, 图1 观测边的边长及方位角Fig.1 Length and azimuth of the observed side 按照GCLM算法可得该观测边的非线性方程组 (18) (19) 解的纠正方程为 (JkTPJk+μkI)dk=-JkTPVk (20) 其平差准则为 ‖JkTPVk‖ε (21) m代表观测值个数;P为观测值的权阵;Vk为第k次迭代所有观测值的改正数;ε为迭代终止条件。 根据上述的函数模型和平差准则利用GCLM算法进行解算,按照GCLM算法的迭代步骤求出式(19)满足准则(21)的最终解,并对坐标平差值进行精度评定 (22) 式(22)中,σ0为验后单位权中误差,Dxx为坐标平差值的方差-协方差阵。 4数据分析 按照GCLM算法在边角网中的应用,以一个单三角形为例,如图2所示,观测了2个内角L1,L2和2条边长S1,S2,各观测值如下:L1=40°23'17.8",L2=93°59'58.7",S1=1 786.372m,S2=2 493.721m,已知A点坐标为(0,0),AB方位角为0。 图2 边角观测的单三角形Fig.2 Triangulateration triangle 可以求得B点和C点较准确的坐标近似值为:XB0=1 786.372m,XC0=1 899.374m,YC0=1 615.841m,称为第1类近似值。以第1类近似值为基础,分别采用几种不同的算法对该单三角形进行平差,将不同算法的结果做了对比,如表1所示。为了对比不同的非线性算法的收敛特性及其平差结果对初值选取的依赖性,更改B和C2点的坐标近似值如表2所示,称为第2类近似值,表2为G-N法与GCLM法基于第2类坐标近似值的解算平差结果对比。 表1 不同算法基于第1类近似值的平差数据对比 表2 G-N法与GCLM法基于第二类近似值的平差数据对比 从表1中可以看出,无论是NTLS算法、G-N算法还是本文的GCLM算法,均可以获得较高精度的坐标平差值,这3种方法的验后单位权中误差均优于传统的LS法和线性化后的牛顿迭代法,且3种方法的验后单位权中误差较差不超过0.1"。从表2可以看出,当坐标近似值较为接近准确值或偏差不大时,G-N算法仍然可以正常进行且验后精度与表1中验后精度相同,即初值选取较为恰当时不会影响G-N算法解算结果的有效性,此时G-N算法与本文的GCLM算法验后精度相差0.02",可以认为2种方法解算精度相当。当B和C 2点坐标近似值偏差很大时,G-N算法无法收敛至坐标真值,而本文的GCLM算法仍然可以顺利进行且精度与表1中精度相当,即初值选取偏差较大时,GCLM算法获得的坐标平差值及验后精度与基于第一类坐标近似值的坐标平差值和验后精度相同。 笔者对模拟的100个单三角形进行了同样的计算,统计结果显示:NTLS算法、G-N算法以及GCLM算法优于传统的LS算法和牛顿迭代法的比例为97%;笔者在这100个单三角形中按照表2中初始值选取的方法对G-N算法和GCLM算法的结果作了统计,当初始值选取偏差很大时G-N算法无法收敛;当初始值选取偏差不大时,GCLM算法解算结果与G-N算法解算结果的比较如表3所示。δ为2种方法的验后单位权中误差较差,P(Δσ0)=P(σGCLM-σG-N),表示验后单位权中误差较差属于不同区间的比例。 表3 GCLM算法与G-N算法的统计结果 从表3可以看出,在待求点坐标迭代初值较为理想的情况下,GCLM算法总体上略优于G-N算法,由于GCLM算法具有一定的收敛优势,因此可以认为在非线性平差问题中GCLM算法略优于传统算法和G-N法,且与NTLS算法相差不大。 5结论 1)GCLM算法优于传统的线性化方法,可以得到更加准确的平差结果,且验后精度明显提高;与G-N等非线性算法相比,GCLM算法可以保证迭代计算全局收敛,克服了G-N法局部收敛的缺点,一定程度上降低了对迭代初值的要求,具有较大的收敛范围,其验后精度与NTLS精度相当。 2)GCLM算法从理论上降低了非线性模型线性化后的模型误差,无论是收敛特性还是验后精度均具有相对优势,是一种有效的非线性参数平差算法。 参考文献: [1] 邓兴升,孙虹虹,汤仲安.高斯牛顿迭代法解算非线性Bursa-Wolf模型的精度分析[J].测绘科学,2014,39(5):93-95. DENG Xingsheng, SUN Honghong, TANG Zhongan.Accuracy analysis of gauss newton iteration method for solution of nonlinear Bursa-Wolf Model[J].Science of Surveying and Mapping, 2014,39(5):93-95. [2] 胡川,陈义.非线性整体最小平差迭代算法[J].测绘学报,2014,43(7):668-674. HU Chuan, CHEN Yi.An iterative for nonlinear total least squares adjustment[J].Acta Geodaetica et Cartographica Sinica,2014,43(7):668-674. [3] 吴玲,刘忠,卢发兴.全局收敛高斯-牛顿法.解非线性最小二乘定位问题[J].火控雷达技术,2003,32(3):75-80. WU Ling, LIU Zhong, LU Faxing.Global convergence Gauss-Newton Method applied to nonlinear least square estimation in target location[J].Fire Control Radar Technology, 2003,32(3):75-80. [4] Yamashita N, Fukushima M.On the rate of convergence of the Levenberg-Marquardt Method[J].Computing,2001(15):239-249. [5] Levenberg K.A method for the solution of certain nonlinear problems in least squares[J].Quart APPL Math,1944:164-166. [6] Marquardt D W.An algorithm for least-squares estimation of nonlinear inequalities[J].SIAM J Appl Math,1963,11:431-441. [7] Fan Jinyan.A modified Levenberg-Marquardt method for singular system of nonlinear equa-Tions[J].Journal of Computational Mathematics,2003,21(5):625-636. [8] 何叶丹,马昌凤.求解非线性方程组的一个修正非单调L-M算法[J].福建师范大学学报(自然科学版),2013(4):21-28. HE Yedan, MA Changfeng.A modified nonmonotone L-M method for solving nonlinear system of equations[J].Journal of Fujian Normal University(Natural Science Edition),2013(4):21-28. [9] 范东明.非线性最小二乘参数平差的非线性规划算法研究[J].西南交通大学学报,2001,36(5):476-480. FAN Dongming.Nonlinear programming algorithms for nonlinear least squares adjustment by parameters[J].Journal of Southwest Jiaotong University ,2001,36(5):476-480. [10] 刘国林,姜岩,陶华学.非线性最小二乘参数平差[J].测绘学报,1998,27(3):224-230. LIU Guolin, JIANG Yan, TAO Huaxue.Nonlinear least souares adjustment by parameters[J].Acta Geodaetica et Cartographica Sinica,1998,27(3):224-230. [11] 游为,范东明.基于改进同伦算法的非线性最小二乘平差[J].西南交通大学学报,2009,44(2):181-185. YOU Wei, FAN Dongming.Nonlinear least squares adjustment based on improved homotopy algorithm[J].Journal of Southwest Jiaotong University ,2009,44(2):181-185. [12] Ma Changfeng,Jiang Lihua.Some research on Levenberg-Marquardt method for the nonlinear equations[J].Applied Mathematics and Computation,2007,184:1032-1040. [13] 宋韬,刘成龙,杨雪峰.工程平面控制网置平平差的方法研究[J].铁道科学与工程学报,2013,10(3):82-86. SONG Tao, LIU Cheng Long, YANG Xue Feng.The research for the method of plane control network adjustment[J].Journal of Railway Science and Engineering,2013,10(3):82-86. [14] 王穗辉.误差理论与测量平差[M].上海:同济大学出版社, 2010. WANG Suihui.Error Theory and Surveying Adjustment[M].Shanghai: Tongji University Press, 2010. [15] 宋力杰.测量平差程序设计[M].北京:国防工业出版社, 2009. SONG Lijie.Program design of surveying adjustment[M].Beijing: National Defense Industry Press,2009. [16] 徐士良.数值分析与算法[M].北京:机械工业出版社,2003. XU Shiliang.Numerical analysis and algorithm[M].Beijing: China Machine Press, 2003. (编辑阳丽霞) Globally convergent levenberg-marquardt method for nonlinear parameter adjustment WANG Lipeng1,2,LIU Chenglong1,2 (1.Faculty of Geosciences and Environmental Engineering, Southwest Jiaotong University, Chengdu 611756, China; 2.State-Province Joint Engineering Laboratory of Spatial Information Technology of High-Speed Rail Safety, Chengdu 611756, China) Abstract:Adopting iterated algorithm of globally convergent levenberg-marquardt could weaken the model error greatly while non-linear model is linearized.Beside, the L-M iterated algorithm is still convergent even Jacobian matrix is approximatively singular.Meanwhile,the algorithm is globally convergent which would weaken the requirement greatly for iterative initial value.This algorithm could gain exact solution even the iterative initial value has a serious error.Through the comparison of different non-linear programming algorithm,it has been proved that iterated algorithm of globally convergent levenberg-marquardt has comparative advanage in accuracy and the range of convergence. Key words:globally convergent;L-M iteration;non-linear parameter adjustment;model error 收稿日期:2015-04-15基金项目:长江学者和创新团队发展计划资助项目(IRT13092) 通讯作者:刘成龙(1962 - ),男,福建莆田人,教授,从事精密工程测量与变形监测;E-mail:wanglpswjtu@sina.com 中图分类号:P207 文献标志码:A 文章编号:1672-7029(2015)06-1452-06