几何非线性对沪通公铁两用长江大桥的影响
2016-01-25张晔芝刘剑光张晓龙
张晔芝,刘剑光,张晓龙
(中南大学 土木工程学院,湖南 长沙 410075)
几何非线性对沪通公铁两用长江大桥的影响
张晔芝,刘剑光,张晓龙
(中南大学 土木工程学院,湖南 长沙 410075)
摘要:在建的沪通公铁两用长江大桥是一座超大跨度、超大体量、超大活载的公铁两用斜拉桥。采用U.L空间非线性有限元分析方法,以主跨跨中挠度最大的活载工况为例,研究3种几何非线性效应对该桥的变形和受力状态的影响。结果表明,3种几何非线性对桥梁的变形和受力状态的综合影响最大达到12.60%(增大);3种几何非线性效应中,斜拉索的垂度效应对于桥梁变形和受力状态的影响最大,达到7.73%,超过了大位移效应和梁柱效应的综合影响;用Ernst公式修正拉索弹模考虑拉索垂度效应的影响时,可用恒载+活载线弹性分析得到的索力,得到的结果较准确而避免了迭代计算;若用恒载索力修正拉索的弹模,将成倍夸大垂度效应的影响,因而是不可行的。
关键词:几何非线性;公铁两用斜拉桥;垂度效应;大位移效应;梁柱效应

在建的沪通公铁两用长江大桥(下称沪通桥)是一座国内外从未有过的超大体量的公铁两用斜拉桥,主桥的孔跨布置为(142+462+1092+462+142)m,全长2 300 m,采用三主桁三索面结构,上层通行6车道公路,正交异性板结构,下层通行4线铁路,闭口钢箱梁结构,钢箱梁的顶、底板都是正交异性板;主桁杆件与下层桥面系形成箱-桁组合结构,桁高16 m,节间长度14 m,桥宽35 m;最长的斜拉索达583.8 m,倾角为 24°,重量达782 kN/m。该桥结构庞大,构造复杂,荷载大,活载作用下主跨跨中的挠度达2 m左右,所以研究分析各种几何非线性因素对于该桥变形和受力状态的影响很有必要。
1斜拉桥的几何非线性
斜拉桥几何非线性可分为3种[1-2]:1)斜拉索的垂度效应;2)梁体的大位移效应;3)主梁、主塔的梁柱效应。
1.1 斜拉索的垂度效应
斜拉索正常工作时受轴力和重力的共同作用,呈悬链线形状,轴力和变形并不是线性关系。斜拉索的长度,角度以及重量越大,斜拉索越松弛,非线性问题越突出。斜拉索轴力的增大,会减小斜拉索的松弛,减小非线性效应。
目前,斜拉索垂度效应的处理方法较成熟是Ernst等效弹模法[3]。近年来有学者提出了多段杆单元法[4-5],多节点曲线索单元法[6-7]和悬链线法索单元法[8-9]等。这些方法通常都将单根索划分成许多梁单元,直线的或曲线的用半解析半数值的方法计算出索的垂度和索力。这些方法目前还处在研究阶段,多数还只用于研究两端固定的单根索的垂度效应,而未用于实际的桥梁,目前通用软件中还未引入他们的研究成果。实践表明,用Ernst公式来修正斜拉索的垂度效应是有足够精度的,而且相对简单、方便,所以本文采用Ernst公式,研究索的垂度效应对沪通桥变形和受力状态的影响。
Ernst等效弹性模量法是根据索的索力、单位长度重量、水平投影长度等来修正索的弹模,计算公式如下:
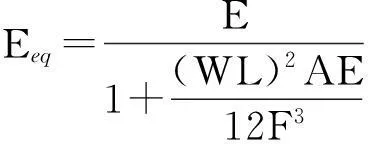
式中:Eeq为拉索等效弹性模量;E为拉索材料的弹性模量,本文取E=1.95×105MPa;W为单位长度拉索的重量;L为拉索的水平投影长度;A为拉索的横截面积;F为拉索索力。
1.2 大位移效应和梁柱效应
大跨度斜拉桥是一种柔性结构,即使在正常工作状态下也会产生较大的变形。节点位置的变化会改变单元的长度、倾角等几何特性,结构的整体刚度也会随之改变。实际上变形后的平衡才是结构的最终平衡状态,在小位移结构分析时,一般忽略结构变形对结构整体刚度的影响。对于大位移结构,若这样分析,就会引起较大的误差。

在线性分析中,认为弯矩和轴力是相互不耦合的。然而在实际情况中,弯矩会引起杆件的侧向位移,由于侧向位移的存在,轴力会产生弯矩,轴力和弯矩相互影响。斜拉桥的主梁和主塔不仅承受很大的弯矩,而且还承受很大的轴力。考虑轴力和弯矩的相互耦合关系得出的计算结果将会更加符合实际情况。
对于沪通桥这样的大型结构,大位移效应和梁柱效应用解析法求解很困难[10-12],用有限元法无困难,但计算量大[13]。本文采用U.L列式法来考虑桥梁的大位移效应和梁柱效应[14]。U.L列式法是在有限元模型变形后的位置上列平衡方程,将荷载分为很多个荷载步,每一个荷载步都经过多次迭代计算出结构的变形,在下一个荷载步的计算中按前一个荷载步完成后的位移列平衡方程。由于在变形后的位置上列平衡方程,不仅考虑了大位移效应,同时也计入了轴力和弯矩的耦合作用,从而考虑了桥梁的梁柱效应。
2有限元分析方法
斜拉桥的几何非线性问题,理论分析是非常困难的,需要作很多假定,把结构简化。简化时结构刚度一般较容易与原结构等效,但结构的强度很难同时与原结构等效,因而算出位移后很难还原出原结构的内力或应力[15]。
随着电子计算机技术的发展,有限单元法得到了越来越广泛的运用,很多大型的有限元软件包也相应出现。应用有限元分析软件可以较方便地对斜拉桥进行变形和受力分析,理论上和方法上都无困难。但是非线性分析的计算量是线性分析的几十倍乃至几百倍。而且沪通桥结构庞大,构造复杂,即使是最不利活载的线弹性分析也需要好几天的时间。所以建立有限元模型时,要保证计算精度,又要控制自由度数和计算规模。经研究对比,采用3层梁格法,通过Midas/Civil建立沪通桥全桥有限元模型。
所谓3层梁格法是指上层公路正交异性板桥面用1层梁格模拟,铁路桥面钢箱梁顶面、底面正交异性板各用1层梁格模拟,合计3层梁格。每一层梁格中,沿横桥向把每一层桥面板划分成许多条带,每一条带包含桥面板和1~2个纵向加强肋,再把这一条带沿顺桥向划成许多梁单元,该梁单元的截面形状和原条带完全一致,从而其强度、拉压刚度、竖弯刚度等也和原条带完全一致。这些顺桥向的梁单元在节点处由横向梁单元相连,每一个横向梁单元为节点两侧半个顺桥向梁单元长度的桥面板组成。下层铁路桥面钢箱梁的顶、底板由实际的横隔板连接成一体,横隔板也划分成横桥向的梁单元,在这些横隔板的梁单元节点处,将顶、底板的有限元节点与其强加刚性约束条件,使钢箱梁的顶、底板在横隔板处连成一体。这种将正交板连续体用梁格代替的基本思想是与将连续体用有限元网格代替的思想是完全一致的,在桥梁结构的有限元分析中也是常用的[16-18]。
主桁、主塔等其他构件也都采用空间梁单元。实际的斜拉索只有抗拉刚度,而无抗压、抗弯、抗剪刚度,实际的斜拉桥中拉索也只受拉,不受压。但有限元分析中,恒载和活载是分开计算的,某些最不利活载工况下,某些斜拉索索力小于恒载索力,相当于活载索力为压,所以采用具有拉压刚度的直索单元,或叫做桁单元。主桁下弦杆与铁路钢箱梁顶底板之间也加之刚性连接。这种全部由梁单元组成的模型计算效率比既有梁单元又有板壳元的板梁单元高许多,而且能保证精度。图1为有限元模型。
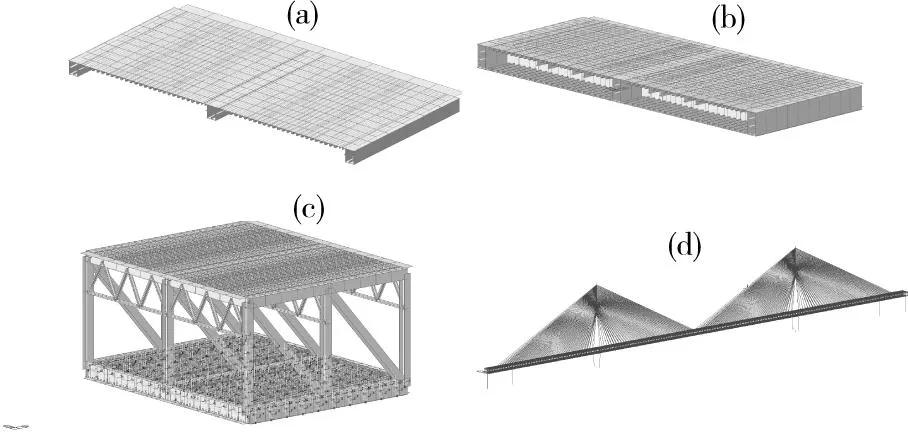
(a)模型中的公路桥面;(b)模型中的铁路桥面(c)模型中的一个节间;(d)全桥模型图1 有限元模型Fig.1 FEM Model
恒载作用下的变形和受力状态是与施工方法和顺序有关,索力是主动张拉的,本文对恒载作线弹性分析,假定恒载作用下的索力将梁体拉至二分之一的活载的上拱度。以主跨跨中挠度最大的最不利工况为例,研究沪通桥几何非线性的影响。在该工况下,主梁的挠度和主塔的顺桥向的位移最大。
活载标准如下:铁路活载采用的是两线ZK活载+两线中—活载。其中城际铁路设计列车活载采用ZK活载,加载长度为550 m,沪通铁路设计列车活载采用中—活载,加载长度为970 m。公路活载采用6线公路I级车道荷载。铁路活载4线折减系数为0.75,公路活载折减系数为0.55。
采用如下4种方法对比分析各种几何非线性效应对该桥的影响:
方法A:线弹性分析,不考虑几何非线性影响;
方法B:只考虑斜拉索垂度效应的影响,用恒载索力+多次迭代得到的活载索力,用Ernst公式修正斜拉索的弹性模量;
方法C:只考虑梁柱效应和大位移效应共同作用,不计斜拉索的垂度效应;
方法D:斜拉索垂度效应、梁柱效应和大位移效应3种几何非线性同时考虑。
3几何非线性影响分析
按上节中A,B,C和D 4种方法对沪通桥作跨中挠度最大活载作用下的有限元对比分析,各个关键部分的内力和位移见表1。
由表1可见,3种几何非线性效应相比,斜拉索的垂度效应对沪通桥变形和受力状态的影响最大,超过了大挠度效应和梁柱效应的综合影响。究其原因,因为拉索长,倾角小,自重大,最长的斜拉索达583.8 m,倾角为 24°,重量达782 kN/m,垂度效应突出。而主梁由于采用上、下层结构,下层是封闭的钢箱梁,桁高达16 m,主梁本身刚度较大,塔柱顺桥向尺寸 14~21 m,也有较大的刚度,所以大位移效应和梁柱效应影响较拉索垂度效应小。
考虑斜拉索的垂度效应后,活载作用下主跨跨中的挠度、塔顶的顺桥向水平位移、主跨跨中上、下弦杆的轴力和塔底的弯矩都有所增加,分别增大了4.99%,4.52%,7.73%,6.50%和3.14%,而桥塔处上弦杆的轴压力减少了3.43%,下弦杆的轴压力和塔底的轴压力也有所减小,但量很小,不足1%。
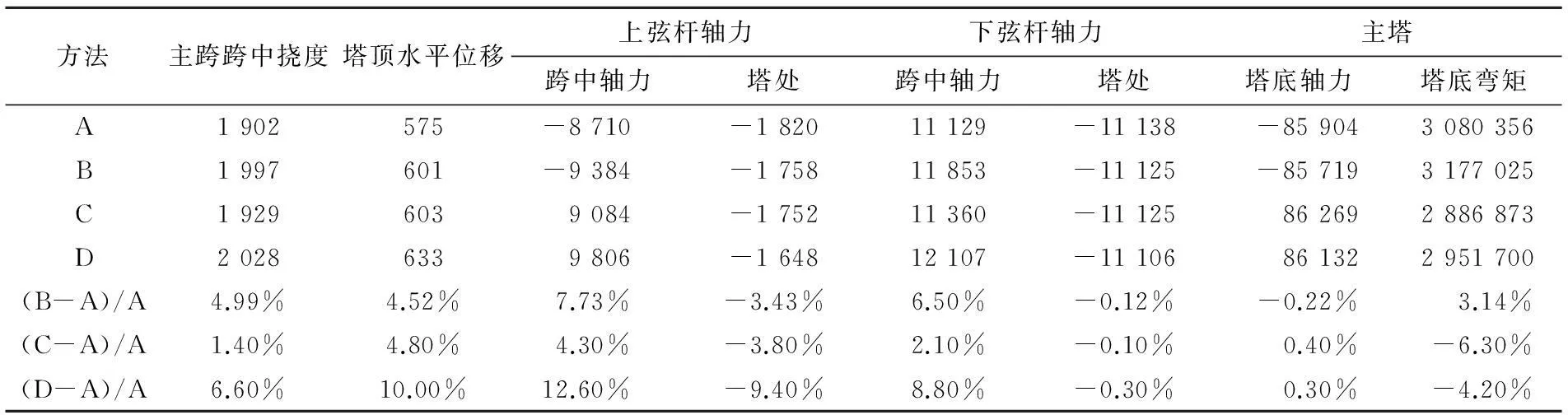
表1 活载作用下关键部位位移和内力对比(力:kN弯矩:kN·m位移:mm)
大位移效应和梁柱效应这2种几何非线性在有限元分析中不能分开单独考虑,所以结果也无法分开。考虑这2种效应的梁体主跨跨中挠度、塔顶水平位移和主跨跨中的上、下弦杆的轴力分别增大了1.40%,4.80%,4.30%和2.10%,而桥塔处上弦杆的轴力和塔底的弯矩分别减少了3.80%和6.30%,而下弦杆在桥塔处的轴力和塔底的轴力变化都小于1%。
3种几何非线性同时考虑时,主跨跨中挠度、塔顶水平位移和上、下弦杆的轴力分别增加了6.60%,10.0%,12.60%和8.80%,而桥塔处上、下弦杆的轴力则分别减少了9.40%和0.30%。
由此可见,主跨跨中挠度最大最不利荷载作用下,受3种几何非线性影响最大的是主跨跨中上弦杆的轴力,3种非线性效应的影响达到12.60%,其次是塔顶的顺桥向水平位移。主跨跨中下弦杆的轴力和主跨跨中的挠度。
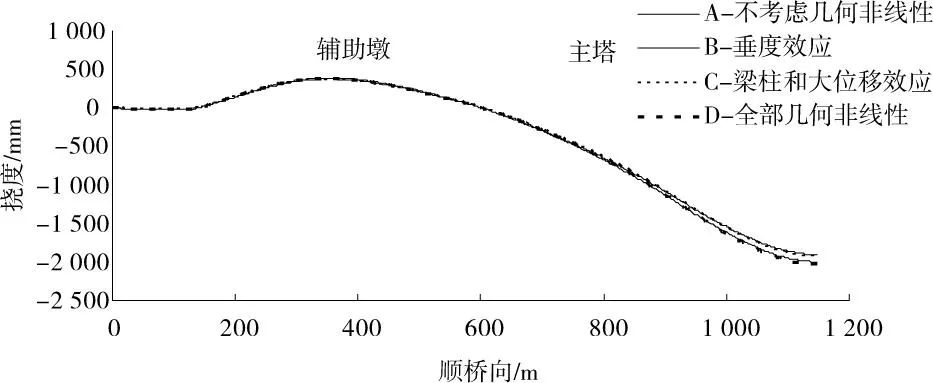
图2 主梁挠度Fig.2 Deflection of the main girder
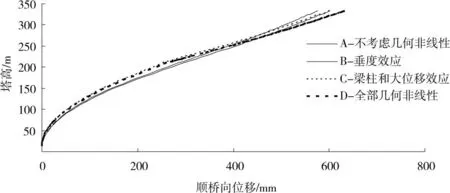
图3 主塔顺桥向位移Fig.3 Displacement of the tower along the bridge
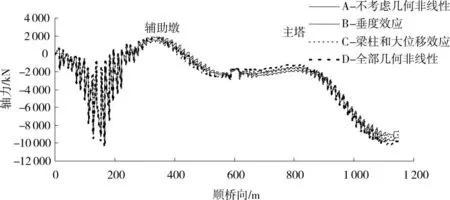
图4 上弦杆轴力Fig.4 Axial forces of the top chord
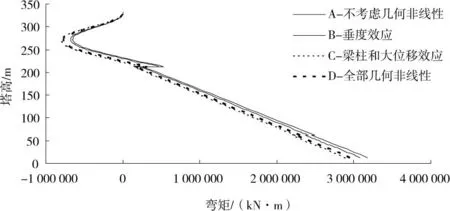
图5 主塔顺桥向弯矩图Fig.5 Moment along the bridge of the tower
图2~图5为主梁挠曲线、桥塔顺桥向位移、上弦杆的轴力和主塔顺桥向弯曲的弯矩,用A,B,C和D 4种方法得到的对比曲线。由于对称,主梁的内力和位移都只画出了半桥。由这些曲线可见,主梁的挠度、上弦杆的轴力,4种分析方法的最大差别发生在主跨跨中,桥塔的顺桥向位移最大差别发生在塔顶,而主塔的弯矩最大差别发生在塔底。
必须指出,上述分析都是对应于主跨跨中挠度最大的活载,对于其他活载工况,几何非线性影响肯定会有所不同。
值得一提的是,在以往斜拉桥的设计中,通常在线性分析的基础上将位移和内力乘以1.1的系数,但对于沪通桥这样特大跨度、特大活载的桥梁,1.1的系数已经不能包住几何非线性的影响。
4斜拉索垂度效应中索力的取值问题
在上节方法B研究斜拉索垂度效应对斜拉桥变形和受力状态的影响时,要用当前的索力来修正拉索的弹性模量。当前的索力是指恒载和当前活载作用下的索力,但是在有限元分析之前并不知道当前的索力是多少,所以要经过几轮迭代计算,方法大致如下。
1)算出恒载索力;
2)假定1组活载索力,用(恒载+活载)索力按Ernst公式修正索的弹性索的弹性模量,用修正后的弹性模量作全桥活载作用下的有限元分析;
3)比较新一轮有限元分析得到的索力和该轮修正弹模所用的索力,若两者差别小于要求,则本轮计算结果是正确的,否则再用新的索力修正索的弹模,直至有限元分析得到的索力与修正拉索弹模的索力基本一致。
有些文献认为考虑拉索垂度效应时可用恒载的索力来修正拉索的弹模[19],这样可避免迭代计算。为考察这种方法的可靠性,本文除了按上面所述方法B外,还用下述B1和B22种方法修正拉索的弹性模量。
方法B1:只考虑斜拉索的垂度效应,用恒载索力,采用Ernst公式修正斜拉索的弹性模量;
方法B2:只考虑斜拉索的垂度效应,用恒载索力+线弹性活载索力,采用Ernst公式修正斜拉索的弹性模量;
将方法A,B,B1和B2修正拉索弹模的部分边桁索力和修正后的拉索弹模Eeq列于表2中,按此弹模所作的有限元分析得到的沪通桥关键部位的变形和受力状态列于表3中。
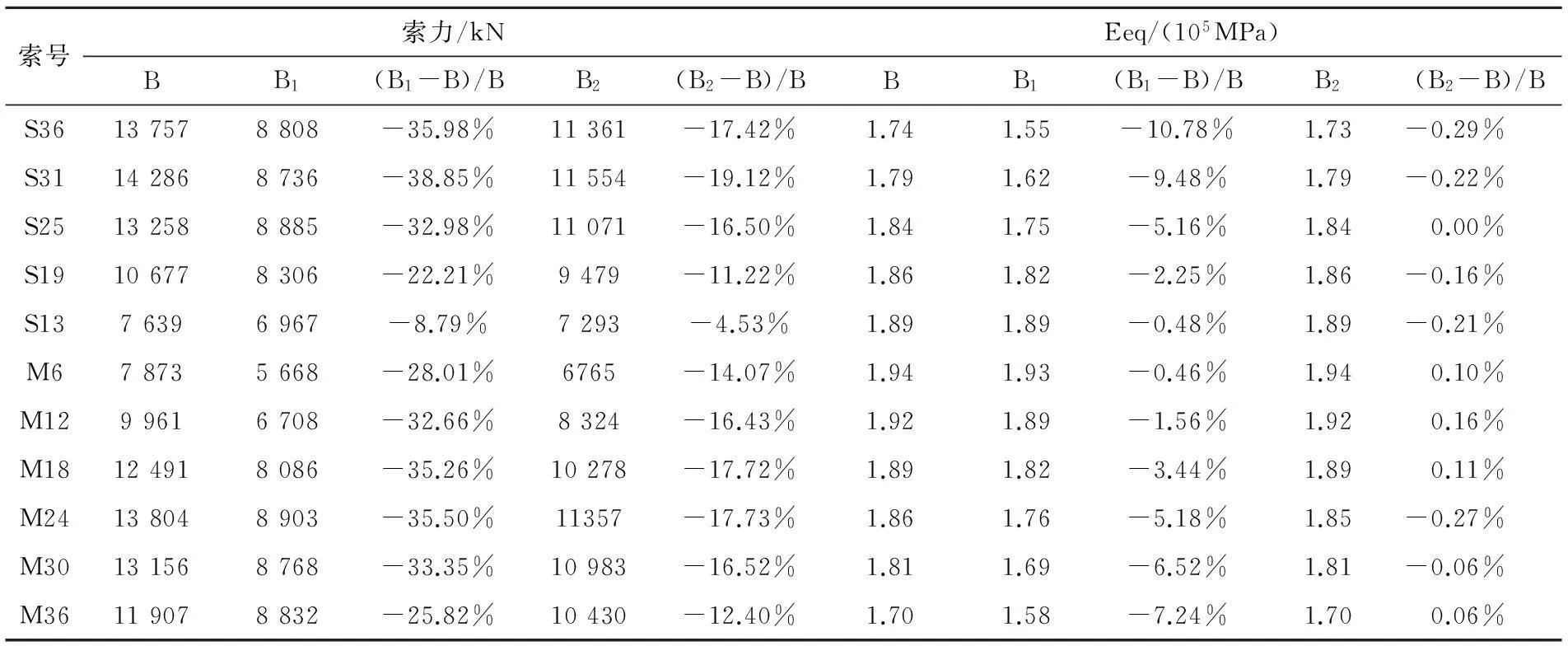
表2 采用不同方法修正拉索弹模的部分斜拉索索力和等效弹性模量
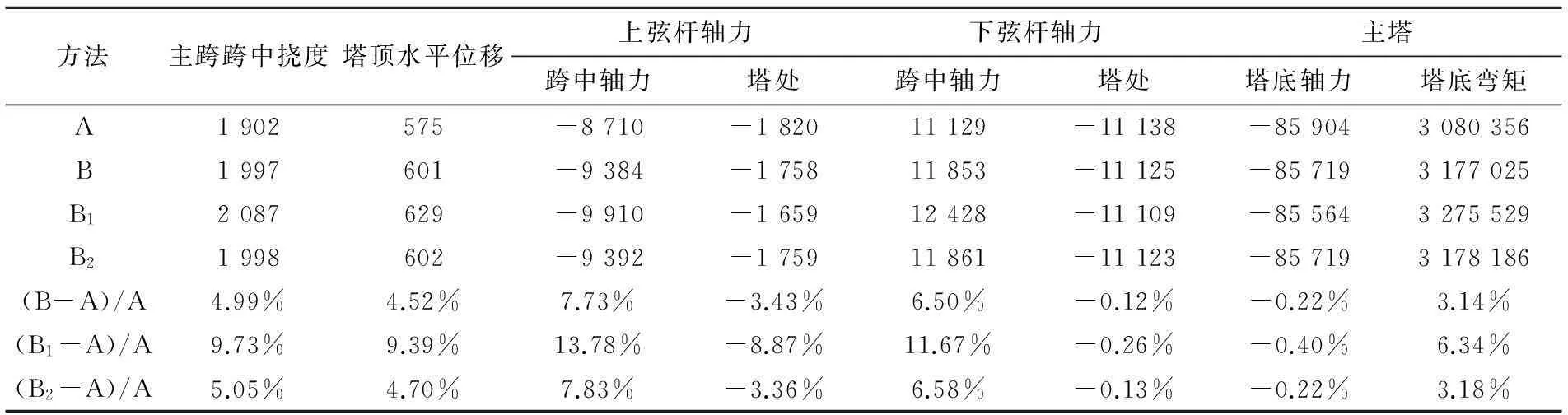
表3 采用不同索力活载作用下关键部位位移和内力(力:kN弯矩:kN·m位移:mm)
表2和表3中方法B修正弹模的索力和考虑垂度效应后有限元分析得到的索力是一致的,因此其值可认为是正确的。方法B1是利用恒载的索力修正E,因索力比B小很多,修正得到的弹模Eeq都偏小,得到的主跨跨中挠度、塔顶水平位移、上下弦杆轴力,与线弹性分析相比,分别增大了9.73%,9.39%,13.78%和11.67%,接近B的2倍,夸大了拉索的垂度效应的影响。由此可见,对于沪通桥这样的公铁两用斜拉桥,由于活载大,用恒载索力修正拉索弹性模量来考虑斜拉索的垂度效应是不可取的。
方法B2是用(恒载+活载)线弹性分析得到的索力来修正拉索的弹模,所得到的Eeq以及有限元分析得到的位移和内力都与B基本一致,所以是可行的,避免了迭代计算。
5结论
1)对沪通桥这样特大跨度、特大体量、特大活载的斜拉桥,斜拉索的垂度效应,梁体的大挠度效应和塔、梁的梁柱效应3种几何非线性对桥梁的变形和受力状态的综合影响最大达到12.60%(增大),常规斜拉桥设计中用1.1的放大系数已经不能包住几何非线性的影响。
2)3种几何非线性效应中,斜拉索的垂度效应对于桥梁变形和受力状态的影响最大,超过了大位移效应和梁柱效应的综合影响。
3)用Ernst公式来考虑拉索垂度效应的影响时,用恒载+活载线弹性分析得到的索力修正拉索弹模,再作有限元分析可得到较准确的结果而避免了迭代计算,所以是可行的;但若用恒载索力修正拉索的弹模,将成倍夸大垂度效应的影响,因而是不可行的。
参考文献:
[1] 伏魁先,刘学信,黄华彪.斜拉桥面内整体失稳分析[J].铁道学报,1993, 15(4):74-79.
FU Kuixian, LIU Xuexin, HUANG Huabiao.An analysis of cabled-stayed bridges on global in-plane instability[J].Journal of the China Railway Society, 1993, 15(4):74-79.
[2] 杜国华,姜林.斜拉桥的合理索力及其施工张拉力[J].桥梁建设,1989(3):11-17.
DU Guohua, Jiang Lin.Reasonable cable forces and tensioning forces of cable-stayed bridge[J].Bridge Construction, 1989(3):11-17.
[3] Ernst H J.Der E-Modul von seilen unter beruecksichtigung des durchhanges[J].Der Bauingenieur,1965,40(2):52-55.
[4] 杨琪.大跨度斜拉桥空间几何非线性仿真分析及其软件开发[D].成都:西南交通大学,2001.
YANG Qi.Geometric nonlinear analysis and software development of large-span cable-stayed bridge [D].Chengdu: Southwest Jiaotong University, 2001.
[5] 苗家武,裴岷山,徐利平.苏通大桥主航道桥几何非线性影响比较研究[C]// 2003年中国公路学会桥梁工程年会论文集.北京:人民交通出版社,2003.
MIAO Jiawu, PEI Minshan, XU Liping.Compare of influence of the geometric nonlinear of main bridge of Sutong bridge[C]// Proceedings of the 2003 annual meeting of the society of China Road and bridge engineering.Beijing: China Communications Press, 2003.
[6] 杨孟刚,陈政清.两节点曲线索单元精细分析的非线性有限元法[J].工程力学,2003,20(1): 42-47.
YANG Menggang, CHEN Zhengqing.The analysis of hysteretic behavior of pall-typed frictional dampers considering geometry nonlinearity[J].Engineering Mechanics, 2003,20(1): 42-47.
[7] 李国平.斜拉索非线性分析的状态修正法[J].同济大学学报(自然科学版),2000,28(1):1-4.
LI Guoping.State revision method in nonlinear analysis of stay cable [J].Journal of Tongji University ( Natural Science), 2000,28(1):1-4.
[8] Kim H K,Lee M J,Chang S E.Non-linear shape-finding analysis of a selganchored suspensionbridge[J].Engineering Structures,2002(24):1547-1559.
[9] 罗喜恒.复杂悬索桥施工过程精细化分析研究[D].上海:同济大学,2004.
LUO Xiheng.Complex fine analysis of construction of suspension bridges[D].Shanghai: Tongji University,2004.
[10] 黄侨,吴红林,刘绍云.大跨度斜拉桥几何非线性分析及程序实现[J].哈尔滨工业大学学报, 2004, 36(11):1520-1523.
HUANG Qiao, WU Honglin, LIU Shaoyun.Long span cable-stayed bridge geometrical nonlinear analysis and it's program[J].Journal of Harbin Institute of Technology, 2004, 36(11):1520-1523.
[11] 吕明.不同跨度斜拉桥变形的几何非线性效应分析[J].工程与建设,2010,24(2):161-163,263.
LÜ Ming.Geometric nonlinear analysis for cable-stayed bridges with different span[J].Engineering and Construction, 2010,24(2):161-163,263.
[12] 王頠,瞿伟廉.大跨度公铁斜拉桥的几何非线性效应[J].华侨大学学报(自然科学版),2009,30(2):215-220.
WANG Wei, QU Weilian.Effect of geometrical non-linearity on long span highway and railway cable-stayed bridges[J].Journal of Huaqiao University(Natural Science),2009,30(2):215-220.
[13] 叶梅新,韩衍群,张敏.ANSYS 二次开发技术在确定斜拉桥初始恒载索力中的应用[J].铁道科学与工程学报, 2005, 2(5):56-59.
YE Meixin ,HAN Yanqun, ZHANG Min.Development and application of ANSYS in long-span cable-stayed bridge[J].Journal of Railway Science and Engineering, 2005, 2(5):56-59.
[14] 徐爱敏,陈衡治,谢旭.结构极限承载力计算方法及其收敛性[J].中国公路学报,2006,19(5):65-70.
XU Aimin, CHEN Hengzhi, XIE Xu.Calculation method for ultimate bearing capacity of structure and its convergence[J].China Journal of Highway and Transport, 2006,19(5): 65-70.
[15] Wang Paohsii,Lin Hungta,Tang Tzuyang. Study on nonlinear analysis of a highly redundant cable stayed bridge[J].Computers and Structures,2002,80(2):165-182.
[16] 王富万,杨文兵.梁格法在桥梁上部结构分析中的应用[J].华中科技大学学报(城市科学版),2006,23(增1):80-82,90.
WANG Fuwan, YANG Wenbing.Application of grillage method in bridge decks analysis [J].Journal of Huazhong University of Science and Technology(Urban Science Edition), 2006,23(Supp1): 80-82,90.
[17] 赖国政, 吕容涛.基于梁格法及板壳有限元法的立交桥空间分析[J].武汉工程大学学报,2008,30(1):37-40.
LAI Guozhen, LU Rongtao.The overpasses spatial analysis based on grillage method and shell element of finite element method[J].Journal of Wuhan Institute of Technology, 2008,30(1): 37-40.
[18] 张发春, 杨昌正.梁格法在弯箱梁桥上的分析及应用[J].重庆交通大学学报(自然科学版),2008,27(1):13-16.
ZHANG Fachun, YANG Changzheng.Analysis and application of grillage method to curved girder bridge[J].Journal of Chongqing Jiaotong University(Natural Science), 2008,27(1): 13-16.
[19] 范立础.桥梁工程[M].北京:人民交通出版社,2012:247.
FAN Lichu.Bridge engineering[M].Beijing: China Communications Press, 2012:247.
(编辑阳丽霞)
Influences of geometric nonlinearity on Hutong combinedhighway and railway Yangtze river bridge
ZHANG Yezhi,LIU Jianguang,ZHANG Xiaolong
(School of Civil Engineering,Central South University,Changsha 410075,China)
Abstract:Hutong Yangtze river bridge under construction is a combined highway and railway cable-stayed bridge with extremely large span, scale and live load.In this paper the U.L nonlinear FEM is used, and the influences of three types of geometric nonlinearity on the deformation and stress status of Hutong Yangtze river bridge are studied with the reference of largest mid-span deflection.The result shows the combined effect of the three types of geometric nonlinearity to the deformation and stress status of the bridge can increase by12.60%.Among the three types of geometric nonlinearity, the effect of cable sag effect is the largest, reaching 7.73%, exceed the combined effect of large displacement effect and girder-tower effect.If the cable elastic modulus are revised according to Ernst figure to considering the influence of the cable sag effect, the cable forces which computed through linear elastic analysis under dead load plus live load can be used.The results have enough precision thus the iterative computations are not needed.If the cable elastic modulus are revised using the cable forces only under dead load, the influence of cable sag effect will be multiple exaggerated, so it is not feasible.
Key words:geometric nonlinearity; combined highway and railway cable-stayed bridge; cable sag effect; large displacement effect; girder-tower effect
通讯作者:张晔芝(1973-),男,上海人,副教授,博士,从事桥梁工程与结构工程教学与科研工作;E-mail: zhangyz824@163.com
基金项目:中国铁路总公司科技研究开发计划课题(2013G001-A-2)
收稿日期:2015-06-26
中图分类号:U448.27
文献标志码:A
文章编号:1672-7029(2015)06-1387-07
