时间序列在黄金价格预测中的应用

徐　宸



时间序列在黄金价格预测中的应用

徐宸

摘要：本文研究了时间序列分析的基本理论，通过Eviews软件对2003～2012年上海黄金交易所各月最后一个交易日的收盘价进行统计分析，建立了二次曲线拟合模型并以此对其进行短期预测，为投资者进行黄金投资提供参考依据。

关键词：时间序列；黄金价格；预测

黄金是可以作为财富的一种度量标准和保值手段。在非常多的方面产生各种各样的影响，都会使黄金价格产生一定的变化。对黄金价格波动需要有一个详细，系统的考量的分析以及对其价格行情进行专业的预测都能有效指导黄金投资者对于黄金的投资。

一、各个影响黄金价格的因素

1、美元对黄金价格的影响

首先，美元作为一个主要货币是国际支付和外汇交易中必不可少的部分，支撑着当前国际货币体系。而黄金所具有的货币职能也让它和美元一同成为重要的储备资产，当美元升值并在国际上处于稳定的地位时，就削弱了黄金作为储备资产和保值功能的地位。其次，国际黄金市场一般以美元作为标价货币，这就导致了当美元贬值时金价会出现上涨的情形。

因此，当美元走强，购买黄金只需要支付少量的美元，这就导致了金价的下跌，反之，就会引起金价的上涨。

2、地势局势对黄金价格的影响

地缘局势的动荡必然引起市场的恐慌，而人们珍藏黄金的很大一部分原因还是出自于黄金规避风险的功能。如果有细心的读者，可以发现在战争或者政治动荡时都会促进黄金价格在短期内的上涨，这就是由黄金的保值属性所决定的。

3、利率对黄金价格的影响

实际利率是银行名义利率，指扣除通货膨胀率后的真实利率，它是影响金价的一个重要因素。当实际利率为负时，显然拿钱去存银行不如买黄金来得划算。

4、股市与商品市场对金价的影响

历史角度来说曾经出现过三个的较大的牛市，它们分别在1906年-1923年、1933年-1953年、1968年-1982年。与此同时，美国股市也出现了长期熊市和加速的通货膨胀阶段。

股票与黄金虽然是两个不同的投资市场，但是两者依然有着千丝万缕的联系。股市对金价的影响主要体现在投资者对打的经济发展方向以及前景的一种预期，如果大部分投资者对经济前景是看好的，那么将会有大量资金流向股市市场，这样黄金市场的投资就会相对减弱，金价就会下跌。反之，就会引起金价的上涨。当然，这样的一种关系并非一成不变的。有时甚至会有一定的正向关系。

5、商品价格指数对金价的影响

在商品市场中，价格趋势对黄金价格也有着一定的影响，因此要研究黄金价格的波动就要对商品的价格做一定的分析。CRB(商品价格指数)能反应不同时期商品价格水平的变化，是研究价格动态变化的一种工具。由于黄金占CRB价格指数权重很高，可以达到了近18%，因此，其价格指数对黄金价格的影响也是很大的。

6、黄金市场指数对金价的影响

美国股票交易所交易的‘金甲虫’指数和在费城股票交易所交易的费城金银指数是代表黄金市场的两个重要指数。两者的主要区别在于金甲虫是由从事对冲交易不足一年半时间的公司构成。

黄金价格上涨是，金甲虫便是一种跟踪金价走势的工具，与现货金价保持了高度的正相关性。而当黄金价格呈下跌趋势时，金甲虫就缺少了避险的保护，因此它的下跌幅度往往会比费城金银指数更大。

二、时间序列分析的基本理论

如果时间序列[X(t)，t=0，±1，±2，…]满足以下三个条件，则称该时间序列为宽平稳时间序列。

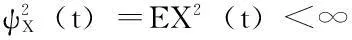
(2)时间序列的均值函数恒为常数，即对任意t∈T=0，±1，±2，…，有E[X(t)]=μ

(3)时间序列的自协方差函数是时间间隔的函数，即对任意t，s∈T=0，±1，±2，…，τ=s-t，有Cov(Xt，Xs)=E(Xt-μ)(Xs-μ)=c(τ)

白噪声是一类典型的平稳时间序列，其特点是：时刻t的随机变量εt与另一个时刻s的随机变量εs是互不相关的，不存在线性关系。

三、我国黄金现货市场黄金价格预测实证分析

1、样本数据的来源

本文选取2003年1月至2012年10月间，每个月最后一个交易日，上海黄金交易所Au9999的收盘价作为样本数据进行统计分析。

2、平稳性检验

由时间序列分析的具体方法可知，应先对选取的样本数据进行平稳性检验，在根据其平稳性建立相关模型。通过Eviews得到样本数据的时间序列如下图：

从上图中可以看出，该序列具有一定的趋势性。

时间序列的样本自相关系数和样本的偏自相关系数如下图：

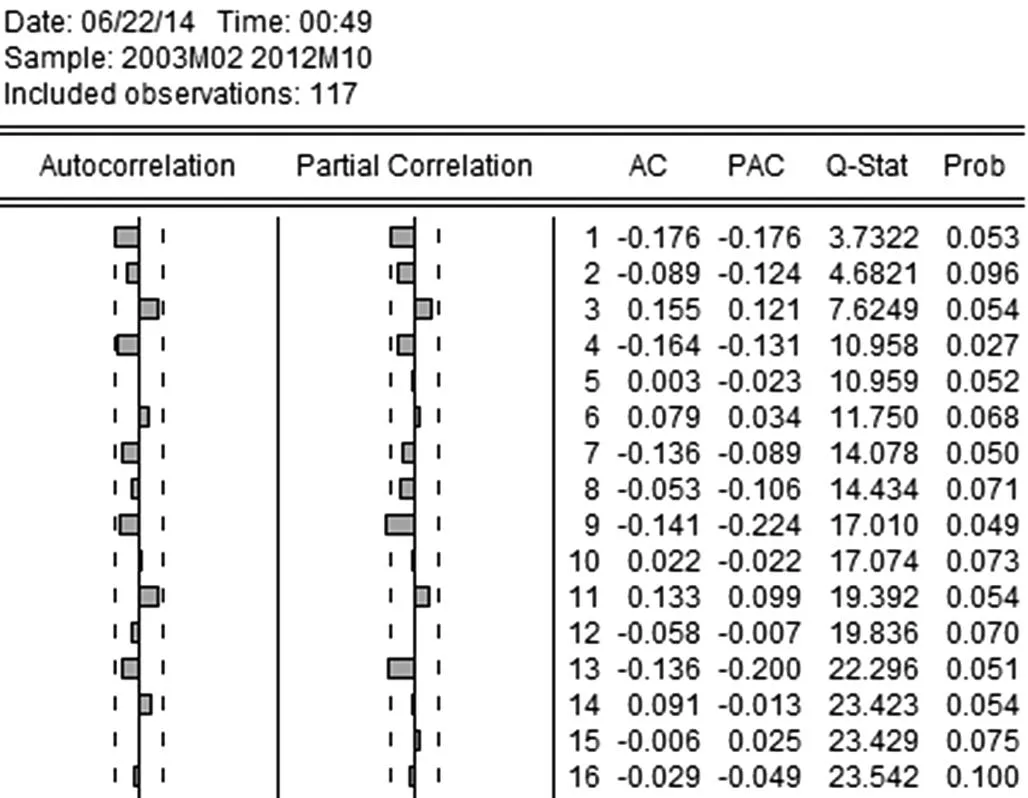
由图可知，该时间序列的样本自相关系数不具有明显递增，递减的特征。从第14个样本开始，“截尾”趋于0。

我们继续进行ADF检验，得到如下图所示：

由图知，在ADF检验中，P值<0.05，说明这是个平稳过程。

3、平稳时间序列的确定性分析

时间序列在较长持续时间内由于受到某种因素的影响，其数据依时间变化而变化。应对该样本运用趋势拟合法通过建立序列值随时间变化的回归模型，来描述时间序列的趋势性。

首先我们确定拟合的最优阶数：

由上图可知，在小样本的情况下，我们确定lag的最优的拟合阶数为3阶。ARMA模型可以更好的拟合数据。图中AIC的最小值已经用“*”标记了出来，该值对应的最优阶数也就是3阶。

由此得出最优拟合模型，即ARMA(3,3)。具体的表示型式为：

Mt=C+β1Mt-1+β2Mt-2+β3Mt-3+θ1Ut-1+θ2Ut-2+θ3Ut-3

使用该模型进行拟合后，我们得到了如下图所示的结果：

我们得到的结果是：

C=15048.69,β1=-0.402950,β2=0.405203,β3=0.997250,θ1=1.218279,θ2=0.608888,θ3=-0.235191

对应的，我们继续列举出它们的标准误差(S.E)与t统计量(t-S)。

由它们的t统计量可以知道对应的P值满足小于0.05。由此我们有理由拒绝等于0的原假设。同时，我们也可以看到R2=0.984256，相关系数很高，证明拟合得很好。有上述各个数据可以说明AMRA(3，3)模型可以很好的拟合这组数据。

最后，我们可以做一个残差平方根的检验，残差平方根都在单位元内部，证明了模型是稳定的。

4、利用拟合模型进行预测

预测2013年1月上海黄金交易所Au9999的收盘价，将其对应值代入拟合模型，得到预测值为350.03122。经查证，实际值为335.68，误差为14.35122。

由于时间序列模型只能用于短期预测，因此长期黄金投资的投资者要更多考虑现实因素。(作者单位：贵州财经大学)

参考文献:

[1]王祖伟，李兆江.世界黄金价格变动特点及未来趋势[J].黄金，2000，21(2)：54-57.

[2]叶慈南, 曹伟丽.应用数理统计[M].北京：机械工业出版社，2009

[3]涂小龙.基于信息修正GM_1_1_模型的黄金价格行情预测，2012

作者简介：徐宸(1990-)，男，汉族，江西上饶人，在读硕士研究生，贵州财经大学，应用统计学经济社会统计与人口统计方向。