Fast ICA盲分离算法在雷达抗主瓣干扰中的应用研究

王文涛，周青松，刘兴华，李　磊

(电子工程学院502教研室，　合肥 230037)



Fast ICA盲分离算法在雷达抗主瓣干扰中的应用研究

王文涛，周青松，刘兴华，李磊

(电子工程学院502教研室，合肥 230037)

摘要：压制干扰信号从主瓣进入雷达天线，会严重影响雷达的性能，通常的副瓣抗干扰技术难以奏效。文中首先给出了Fast ICA应用于雷达抗主瓣干扰的信号模型；在高信噪比的均匀噪声环境中，利用基于寻找峭度的局部极值点的Fast ICA盲分离算法分离接收到的主瓣干扰混合信号，通过脉压找出目标信号。仿真验证了算法用于抗主瓣干扰的有效性，该算法具有良好的抗干扰性能，在分离效率上具有较明显的优势。

关键词：抗主瓣干扰；峭度；Fast ICA盲分离算法；脉压

0引言

现代电子战中，千方百计提高雷达的抗干扰性能已成为雷达设计师所面临的严峻任务。为了提高雷达在复杂电磁干扰环境中的生存能力，已经采用了超低旁瓣、旁瓣匿影、旁瓣对消等抗干扰措施。但当干扰信号从主瓣进入雷达天线时，通常会严重影响雷达的性能，副瓣抗干扰措施无能为力。

文献[1]利用和差波束的主瓣对消可以抑制近主瓣干扰，但是必须将主波束对准目标，这在复杂电磁环境中难以实现。文献[2-3]利用阻塞矩阵对接收数据预处理，然后自适应波束形成抑制主瓣干扰，但存在主波束指向偏移的问题。文献[4-5]利用天线的“空域极化特性”研究了极化域滤除主瓣干扰的新方法。文献[6]研究了基于特征矩阵近似联合对角化(JADE)盲源分离(BSS)的抗主瓣干扰技术，但是，JADE盲分离算法中，求解观测信号的高阶累积量以及两次特征分解

的运算，一定程度上影响了算法的分离速率，而且当阶数高的时候，对矩的估计可能会出现较大的误差，这就影响了算法的分离效率，从而影响了利用其抗干扰的性能。

本文首先给出了Fast ICA应用于雷达抗主瓣干扰的信号模型，在此基础上，当高信噪比时在均匀噪声环境中，应用基于寻找峭度的极值点的Fast ICA盲分离算法实现了抗雷达主瓣干扰。仿真结果验证了算法良好的抗干扰性能，表明了本文算法相比基于JADE的抗主瓣干扰算法和自然梯度盲分离算法[7]应用于抗主瓣干扰时，在分离效率上具有较明显的优势。

1信号模型

考虑相控阵雷达，阵列天线有N个接收传感器；雷达信号为脉冲信号。接收信号为一个目标回波和多个压制干扰信号的混合信号，其总数为M，经过未知传输信道，在传感器阵列上得到N路观测信号。由于混合信号分别来自不同的信号源，可以假设各个源信号之间是相互独立的，在线性瞬时混合的条件下，不受噪声“污染”的理想的数字化混合接收模型的数学表示为

x(k)=As(k)

(1)

如果在加性噪声n(k)的环境下，数字化混合接收模型的数学表示为

x(k)=As(k)+n(k)

(2)

式中：k为采样时刻；x(k)=[x1(k),x2(k),…,xN(k)]T；A是一个N×M维混合矩阵，A=[a1,a2,…,aM]，是由M个N维列向量组成；s(k)=[s1(k),s2(k),…,sM(k)]T，那么n(k)=[n1(k),n2(k),…,nN(k)]T。

需要说明的是，盲源分离算法要求混合矩阵A是N×M维列满秩矩阵[8]，即要求接收通道数目不小于目标和干扰信号数目总和(N≥M)。在下面的内容中，我们均假设接收传感器满足N=M。

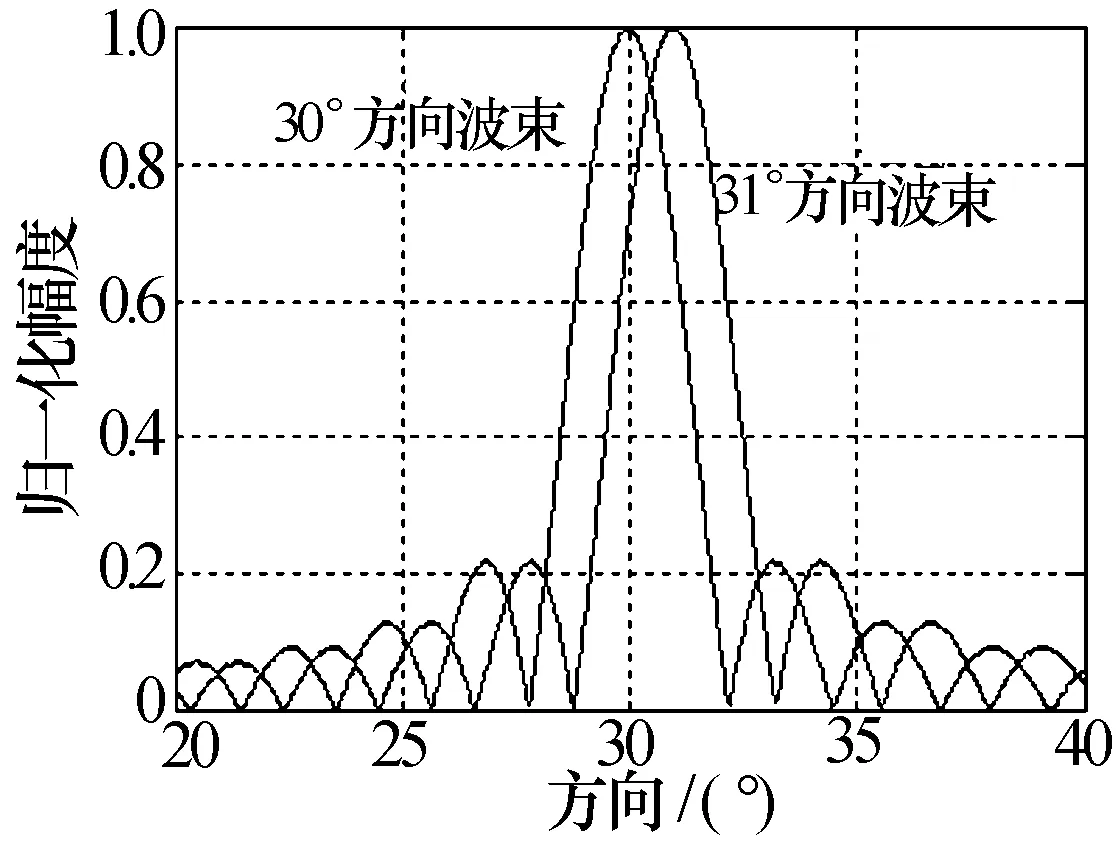
图1　双波束接收方向图

这里，以一个目标信号和一个主瓣干扰信号，并采用两个通道接收信号的情形为例，说明主瓣干扰信号接收模型。假设目标位于30°方向，干扰位于31°方向，通道1接收到30°方向波束信号，通道2接收到31°方向波束信号，如图 1所示，那么30°方向波束信号可以表示为

x1(k)=a11s1(k)+a12s2(k)

(3)

31°方向波束信号可以表示为

x2(k)=a21s1(k)+a22s2(k)

(4)

那么，抗干扰的目的就是要确定常量线性变换矩阵W使得y=Wx，并从y中找出目标信号(假设为y1(k))和干扰信号yn(k)(n=2,3,…)，然后通过对干扰信号分析，从而更有效地调度抗干扰资源。

2基于Fast ICA的抗主瓣干扰算法

盲信号分离技术[8]应用于混合信号分析处理是近年来一个热门的研究领域。文献[9]提出了经典的基于寻找峭度的局部极值点的Fast ICA盲分离算法，本文将其应用于对抗雷达的主瓣干扰。首先考虑理想情况(式(1))的信号模型下的Fast ICA算法，然后讨论算法在“带噪”(式(2))模型下的应用，并给出应用Fast ICA分离主瓣干扰混合信号的完整流程。

2.1预处理

按照BSS一般的做法，对接收数据进行预处理。具体步骤如式(5)和式(6)

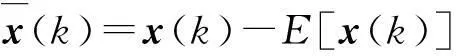
(5)

(6)

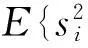
(7)

如果考虑噪声的影响，这里假设均匀高斯白噪声，噪声协方差矩阵Σ是已知的。如果观测的“带噪”数据协方差矩阵为C=E{xxT}，那么，通常的白化应该用下式代替

(8)

即就是转化后，能得到白化信号如下

z(k)+v(k)

(9)

2.2理想环境中的Fast ICA

在雷达信号处理中，为了说明Fast ICA在抗干扰中的有效性和可行性，本节忽略噪声的影响，考虑算法对“无噪”模型(式(1))的干扰混合信号的分离。

基于峭度的Fast ICA盲分离算法，是以梯度下降(或者上升)的在线学习算法为基础，通过寻找观测信号线性组合的峭度的局部最大值(或者最小值)，从而找出各个独立分量。峭度的定义式可以表示为

(10)

kurt(WTBs(k))=kurt(HTs(k))=

(11)

在‖W‖=‖H‖=1的约束下，式(11)可以取得局部最大值(或者最小值)，每一个局部极值点可以取得一个非高斯的独立分量。

为了最大化或者最小化kurt(WTz(k))，由于信号已经白化处理，在‖W‖=1的约束下，目标函数可以简化为

kurt(WTz(k))=E{(WTz(k))4}-3E2{(WTz(k))2}=

E{(WTz(k))4}-3‖W‖4

(12)

下面考虑单个信号抽取的算法。把满足约束条件的一个函数F(‖wi‖2)作为罚项，给式(12)增加一个罚项，得到最终的无约束目标函数如下

(13)

对式(13)求导，有

3‖wi‖2wi+f(‖wi‖2)wi

(14)

其中

f(‖wi‖2)=dF(‖wi‖2)/(2 d(‖wi‖2))

那么，可以得到如下的在线学习算法

wi(t+1)=wi(t)±μ(t)[E{z(t)(wi(t)Tz(t))3}-

3‖wi(t)‖2wi(t)i+

f(‖wi(t)‖2)wi(t)]

(15)

式中：t表示第t次循环；方括号前面的正号表明寻找局部极大值点；负号表示寻找局部极小值点。而在线学习算法中，步长因子μ的选择很重要，μ选择较差会使得算法收敛性能下降。下面给出收敛速度更快的迭代算法，令式(14)等号右边为零，即

(16)

由式(16)解得

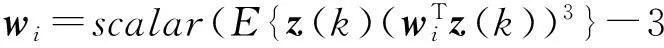
(17)

式中：scalar=-1/f(‖wi‖2)是标量，对wi的方向没有影响，可以令scalar=1。

最后需要注意的是，上面是单信号抽取的固定点算法。扩展到多路信号的抽取算法，只需要将上面单信号抽取算法重复n次。但是需要考虑的是，防止各路迭代收敛到相同的最大值，所以每次迭代后必须去除各路输出信号的相关性，可以采用式(18)的方法去相关

W=(WCWT)-1/2W

(18)

式中：W=(w1,w2,…,wn)T。基于以上分析，那么得到的分离信号就为

y(k)=WTz(k)

(19)

2.3Fast ICA在均匀噪声环境中的实现

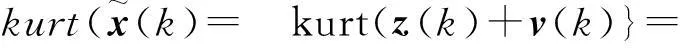
kurt(z(k))+kurt(v(k))

(20)

kurt(v(k))=E{v4(k)}-3E2{v2(k)}=

(21)

那么同样有式(22)成立

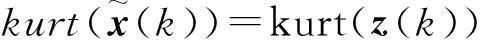
(22)

E{(WTz(k))4}-3‖W‖4

(23)

单信号抽取算法：

(1) 接收信号预白化。

(2) 初始化：t=1，wi(t=0)(t为循环次数)。且归一化：‖wi(0)‖=1。

(4) wi(t)进行归一化处理：wi(t)=wi(t)/‖wi(t)‖。

将其扩展到多路信号分离的算法：

(1) 接收信号预白化。

(2) 初始化：t=1，W(t=0)，W(0)各列之间正交归一化处理。

(4) 对W(t)进行列去相关，归一化处理。

(5) 如果WT(t)W(t)尚未接近单位矩阵，那么使t=t+1，返回到(3)；否则，结束循环。

2.4信号盲分离后处理

(24)

式中：conv(·)为卷积运算。通过脉压以后的峰值检测，可以确定出雷达回波信号，也可以对干扰波形进行分析，从而实现雷达抗主瓣干扰。

3仿真实验

实验中假设阵列天线为均匀线阵，阵元间距为λ/2，采用60个阵元；雷达发射信号为线性调频信号(LFM)，信号带宽1 MHz，脉宽100 μs，采样点1 000个；干扰信号为噪声调频信号，干信比为30 dB；仿真中噪声以复信号的形式表示。为模拟主瓣干扰，假设目标信号位于30°方向，干扰信号位于31°方向，采用双波束接收，波束宽度2°，主瓣接收模型如图1所示。

实验1：验证算法用于抗主瓣干扰的有效性

当信噪比为10 dB，其他仿真条件不变时，由于干扰信号太强，两路接收信号在盲分离前脉压不能检测出目标信号。应用本文算法并脉压处理的仿真结果如图2所示。

图2　Fast ICA算法盲分离前后脉压波形对比(10 dB)

从图2b)中盲分离后尖峰可以看出，信噪比10 dB时Fast ICA对主瓣干扰的抑制超过20 dB，从整个脉压波形来看，可以看出图2b)的脉压波形已经比较接近纯线性调频信号的脉压波形，这表明信噪比较大时，算法对主瓣干扰混合信号良好的分离性能。

而当信噪比为-10 dB，其他实验条件不变时，采样前对两路混合信号作脉压处理，由于干扰信号和噪声太强，两路信号都不能检测出目标信号的存在。采用本文算法分离混合信号，图3是盲分离前任意一路脉压波形和分离后有信号的一路脉压波形对比，图3b)的分离信号脉压后可以看出有明显的尖峰，盲分离对干扰的抑制约为12.6 dB。

图3　Fast ICA算法盲分离前后脉压波形对比(-10 dB)

相同的仿真条件，将采用JADE盲源分离算法的情况与图3作对比，分离后脉压波形如图4所示，可以看出干扰也被抑制了13 dB左右，说明本文算法与JADE算法均能有效地抑制主瓣压制干扰和噪声对目标信号的“淹没”。

图4　JADE算法盲分离后脉压波形(-10 dB)

实验2：算法应用于抗主瓣干扰的性能评价

为了定量评价算法的抗主瓣干扰效果，即就是要评价盲分离算法的性能。这里引入分离信号y(k)与源信号s(k)的相似系数作为评价指标，即

(25)

当ξij为1时，说明y(k)和s(k)的对应信号分量只在幅度上有差异，即yi=csj，c为常数；当ξij为0时，说明两信号完全独立；当ξij越接近1时，明分离信号和源信号的相似程度越高，即分离效果越好。

对实验1中信噪比为-10 dB的混合接收信号，分别应用本文的算法、JADE算法和自然梯度盲源分离算法，对盲分离后的结果求其相似系数矩阵ξ；并且对三种方法各做100次独立重复实验，计算机记录分离算法运算时间，得到结果如表1所示。

表1　三种算法相似系数和运算时间

从表1可以看出，对比JADE算法，本文算法在运算时间上稍小，但也因此牺牲了部分的分离性能，JADE算法的相似系数矩阵要优于本文算法。本文算法相似系数矩阵次对角线上的值虽然较大，但其主对角线上的两个值都比较接近1，表明算法能较准确地恢复目标信号和干扰，而干扰信号的恢复有利于对其进行准确分析；本文算法与自然梯度算法对比可以看出，自然梯度算法的运算时间远大于本文算法，而且其相似系数矩阵要稍差于本文算法，所以其分离效率要差于本文算法。

为了进一步说明本文算法的分离效率，比较同样是迭代寻优的本文算法和自然梯度盲分离算法。从正交归一化的分离矩阵列矢量‖wi‖2=1得到启发，可以定义下面的评价指标

(26)

式中：k为迭代次数，当性能指标P的值越接近0说明分离的效果越好。所以算法可以假设当满足P<ε(ε为设定的小正数)时跳出循环。如果我们固定同样的循环次数，记录每一次迭代的P就能得到如图5所示的收敛性能曲线。

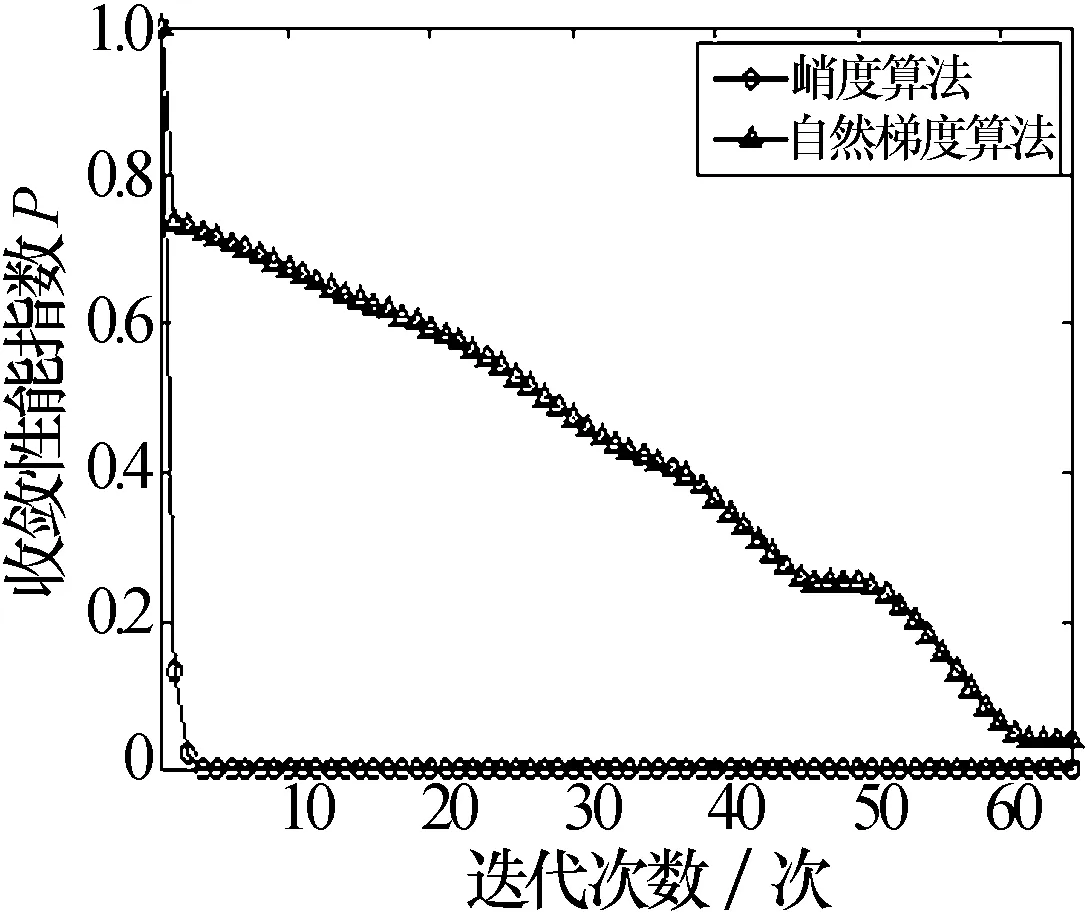
图5　收敛速率曲线

从图5可以看出本文算法在迭代5次以后就趋于稳定，而自然梯度算法则需要迭代62次才能达到稳定的状态。较快的收敛性能进一步说明了本文算法在分离速率上的优势。

结合表1的相关分析：充分表明本文算法相比其他两种算法在分离效率上有一定的优势，这也就间接说明了本文算法应用于雷达抗主瓣干扰时优良的性能。

4结束语

针对主瓣压制干扰严重影响雷达性能问题，本文给出了Fast ICA应用于抗主瓣干扰的信号模型，在此基础上在高信噪比的均匀噪声环境中，应用基于寻找峭度的局部极值点的Fast ICA盲分离算法分离接收到的主瓣干扰混合信号，并脉压找出目标信号，实现对主瓣干扰的抑制。仿真结果显示：当信噪比为10 dB时，算法可以将干信比为30 dB的噪声调频干扰抑制超过20 dB。并且仿真结果表明了本文算法相比于其他两种基于BSS的抗主瓣干扰算法在分离效率上较明显的优势。

参 考 文 献

[1]KAI B Y, DAVID J M. Adaptive digital beam forming for preserving monopulse target angle estimation accuracy in jamming[C]// Proceedings of the 2000 IEEE Sensor Array and Multichannel Signal Processing Workshop. Cambridge, MA: IEEE Press, 2000: 454-458.

[2]李荣锋, 王永良, 万山虎. 主瓣干扰下自适应方向图保形方法的研究[J]. 现代雷达, 2002, 24(3): 50-53.

LI Rongfeng, WANG Yongliang , WAN Shanhu. Research of reshaping adapted pattern under mainlobe interference conditions[J]. Modern Radar, 2002, 24(3): 50-53.

[3]苏保伟, 王永良, 李荣峰, 等. 阻塞矩阵方法对消主瓣干扰[J]. 系统工程与电子技术, 2005, 27(11): 1830-1832.

SU Baowei, WANG Yongliang , LI Rongfeng, et al. Novel research on main-loke jamming pularization suppression technology[J]. Systems Engineering and Electronics, 2005, 27(11): 1830-1832.

[4]戴幻尧, 李永祯, 刘勇, 等. 主瓣干扰极化抑制的新方法[J]. 中国科学:信息科学, 2012, 42(4): 460-468.

DAI Huanyao, LI Yongzhen, LIU Yong, et al. Novel research on main-lobe jamming polarization suppression technology[J]. Science China: Information Science, 2012, 42(4): 460-468.

[5]王峰, 雷志勇, 李婧. 一种自适应正交虚拟极化抗主瓣干扰方法研究[J]. 中国电子科学研究院学报, 2013, 8(1): 53-55.

WANG Feng, LEI Zhiyong, LI Jing. Mainlobe jamming suppression using orthogonal virtual polarization[J]. Journal of CAEIT, 2013, 8(1): 53-55.

[6]王建明, 伍光新, 周伟光. 盲源分离在雷达抗主瓣干扰中的应用研究[J]. 现代雷达, 2010, 32(10): 46-49.

WANG Jianming, WU Guangxin, ZHOU Weiguang. A study on radar mainlobe jamming suppression based on blind source separation algorithm[J]. Modern Radar, 2010, 32(10):46-49.

[7]AMARI S, CICHOCKI A, YANG H H. A new learning algorithm for blind signal separation[C]// Advances in Neural Information Processing Systems 8. Cambridge MA: MIT Press, 1996: 757-763.

[8]张贤达, 保铮. 盲信号分离[J]. 电子学报, 2001, 29(12): 1766-1771.

ZHANG Xianda, BAO Zheng. Blind source separation[J]. Acta Electronica Sinica, 2001, 29( 12): 1766-1771.

[9]HYVARINEN A, OJA E. A fast fixed-point algorithms for independent component analysis[J]. Neural Computation,1997,9(7): 1483-1492.

[10]HYVARINEN A. Gaussian moments for noisy independent component analysis[J]. IEEE Signal Processing Letters,1999,6(6): 145-147.

A Study on Radar Mainlobe Jamming Suppression Based on

Blind Source Separation of Fast ICA

WANG Wentao，ZHOU Qingsong，LIU Xinghua，LI Lei

(502 Department, Electronic Engineering Institute,Hefei 230037, China)

Abstract：If the suppress jamming pour into the mainlobe of radar antenna, it would severely degenerate the performance of radar. The common ECCM measures of sidelobe have no effect. In this paper, the signal model of mainlobe jamming suppression based on Fast ICA blind source separation algorithm is given first of all. Then the blind source separation algorithm of fast independent component analysis (ICA) based on kurtosis in the uniform noise environment is used to separate the high SNR composite signal which is interference and target signal mixed. And the target signal is found out by applying the pulse compression technique between the transmitted target signal and the separated signal at last. Then some simulation experiment is finished to test the validity and to evaluate the performance of the mainlobe jamming suppression algorithm. The simulation results show the satisfactory validity of algorithm in the radar mainlobe jamming suppression and evident superiority in the efficiency of the separation.

Key words：mainlobe jamming suppression; kurtosis; fast independent component analysis; pulse compression

收稿日期：2015-07-20

修订日期：2015-09-18

通信作者：王文涛Email：wangwentao517@126.com

中图分类号：TN972

文献标志码：A

文章编号：1004-7859(2015)12-0040-05