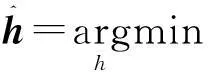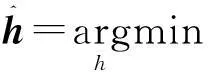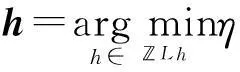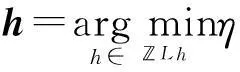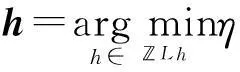基于压缩感知的超分辨目标散射中心估计
2016-01-22晋本周
晋本周,吴 刚
(南京电子技术研究所, 南京 210039)
基于压缩感知的超分辨目标散射中心估计
晋本周,吴刚
(南京电子技术研究所,南京 210039)
摘要:针对雷达目标识别中散射中心特征提取需求,提出一种基于压缩感知理论(CS)的超分辨散射中心估计算法。通过设计一字典,将脉压波形进行稀疏表示,进而将重构问题引入CS理论框架之下,利用仿真数据验证了散射中心重构算法的可行性。基于实录数据,将80 MHz宽带信号滤波成20 MHz窄带信号,利用窄带20 MHz脉压波形重构高分辨散射中心,进而恢复宽带80 MHz脉压信号。恢复信号与真实80 MHz宽带脉压信号的对比分析结果表明,在一定误差范围内,CS算法可实现目标散射中心重构。
关键词:目标识别;压缩感知;超分辨;散射中心
0引言
机载雷达对海工作时,覆盖范围广,可达数十万平方公里。由于海面目标众多,且军民交织,严重影响对重点目标的提取和上报,迫切需要雷达具备目标识别能力[1]。
稳定、差异性特征提取是目标识别的关键[2-3]。目标一维距离复包络是各距离单元内所有散射中心回波的相干叠加,反映了目标结构、大小、几何形状等丰富信息,且容易获取,在目标识别领域受到越来越多的关注[4-6]。文献[7-8]基于一维距离像(HRRP)提取HRRP幂变换、双谱等作为识别特征,通过与模板库数据匹配进行识别。由于机载雷达对海探测姿态角测量精度差,当待识别目标较多时,识别效果不佳。文献[9]研究了基于HRPP统计特征的识别方法,但统计模型参数估计需要大量的数据,实际中往往难以满足。文献[10]提取HRRP中心矩、波形熵、偏度系数、峰度系数等波形特征用于识别,但其中的某些特征缺乏物
理含义,且不同目标特征值分布区间交叠,区分度不够。
目标散射中心相对位置及幅度代表了目标精细物理结构信息,且具有姿态敏感性低等优点,已成为特征提取领域研究热点之一[11]。目前,常规散射中心估计算法大多基于现代谱估计和多维参数估计方法。此类方法首先估计散射中心数目,然后基于散射中心模型进行参数估计,如果散射中心数目和模型偏离实际情况,将导致估计效果恶化。
通常,目标强散射中心数目远小于一维距离像点数,即强散射中心在时域是稀疏的,本文基于CS理论提出一种新的超分辨散射中心估计算法。
1CS理论基本原理
DONOHO[12]、CANDES[13]等提出CS理论,为稀疏信号的观测与重构提供了理论基础。假设x∈N×1为实信号向量,有如下线性表示
(1)
式中:Ψ=[ψ0,ψ1,ψ2,…,ψN-1]为一组基函数;θ=[θ0,
θ1,…,θN-1]T为信号x在基Ψ下的系数向量,i∈{0,1,…,N-1}。如果系数向量θ中非零元素个数k≪N,则在基Ψ下,x是k-稀疏的。
CS理论可概述为:如果信号x是稀疏的,即x可以在某个基矩阵Ψ下稀疏表示,通过一个随机观测矩阵Φ∈M×N对x进行观测,得到M个观测点向量y,观测过程为y=ФΨθ,如果Φ和Ψ不相关,那么,即使M≪N,仍然可以以很高的概率从观测向量y中实现对原始信号x的重构。CS理论原理框图如图1所示。

图1 CS理论原理框图
基于CS理论,从y中重构原始信号x的本质是找一个稀疏的,且满足约束方程y = ФΨθ的向量。那么,重构问题可以转化为求解如下问题

(2)
式中:A=ΦΨ。式(2)是一个NP难问题,目前已经存在很多求解算法,主要包括l1范数凸优化和追踪系列算法。
在一定条件下[14],式(2)可以转化为如下一个凸优化问题

(3)
式(3)是一个l1范数凸优化问题,称为基追踪问题,可以方便地将其转化为一个线性规划问题来求解。
实际中,观测信号中通常含有噪声,假定噪声是加性的,即观测信号y=Aθ+w,其中w为M×1维噪声向量。该情况下,式(3)进一步归结为如下优化问题
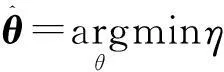
(4)
式中:参数η≥0用来平衡目标函数中的噪声和信号分量,文献[15]对该参数的选取进行了讨论。式(4)可以转化为二次规划问题求解。
2目标散射中心重构
2.1接收信号的稀疏表示
假设雷达发射信号为线性调频波形x(t),如图2所示,经无线信道作用后,接收信号r(t)可表示为
r(t)=x(t)⊗h(t)+n(t)
(5)
式中:h(t)为无线信道冲击响应;n(t)为加性噪声。

图2 接收信号
经接收机端匹配滤波,即脉压处理后,观测信号y(t)可表示为
i=1,2,…,Lh-1
(6)
式中:δ(t)为冲击信号;ai和τi分别表示第i个散射中心回波幅度和延时;⊗表示卷积。目标散射中心估计即是从观测信号y(t)中估计Lh和如下两个参数向量:a=[a1,a2,…,aLh]和τ=[τ1,τ2,…,τLh]。
引入一字典Θ={ρ1(t),ρ2(t),…,ρm(t),…,ρN(t)},字典中的任意一元素为
ρm(t)=sinc(t-mΔτ)
(7)
式中:sinc(t)最大值为1;Δτ为时间分辨率。
当Δτ足够小时,散射中心延迟时间τi近似表示为Δτ整数倍,即任何一个散射中心脉压后波形均可用字典Θ中的元素表示,令τi=mΔτ,进一步地,可以将式(6)表示为
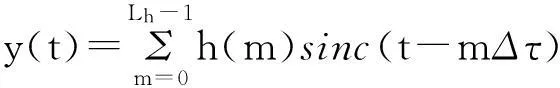
m=1,2,…,Lh
(8)
那么,y(t)可以用一个Lh×1维复向量h表示,h的任意一元素为
h(m)=
(9)
由式(9),可将Lh,a和τ估计问题转化为估计向量h。
通常目标仅有若干个强散射点,散射点数目远小于宽带一维距离像维数,即Lh≫L,h为Lh-稀疏向量。
h的每一个非零元素及其位置分别代表了不同散射中心的幅度和相位,那么,散射中心估计问题就可以看成对向量h的重构问题,由此,将参数估计问题引入到CS理论框架之下。
需要指出,Δτ是虚拟采样间隔,决定了散射中心估计中的距离超分辨能力,本文中取Δτ为1/10采样间隔,即Δτ=Ts/10,Ts为采样间隔,那么,超分辨距离单元距离分辨率为cTs/20,其中c为光速。
2.2散射中心重构
以离散形式(8)可以重新表示为
y=Φvh+n
(10)
其中,矩阵Φv为
(11)
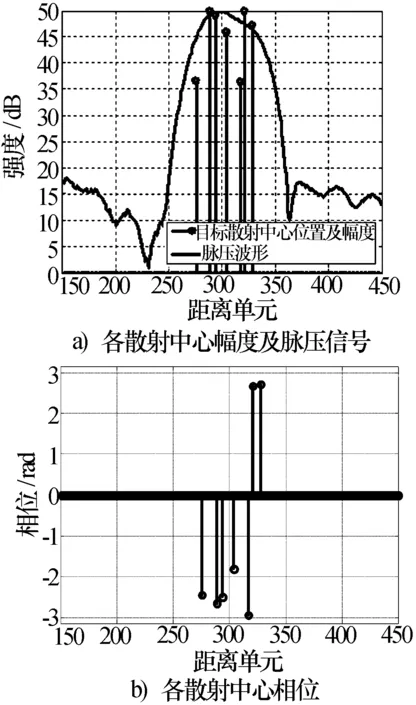
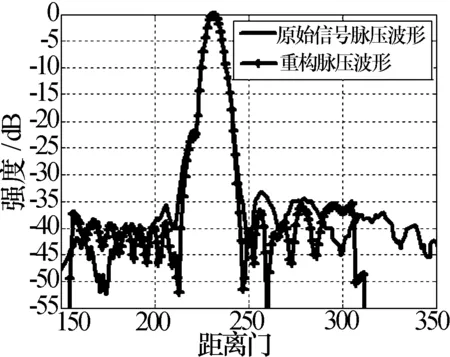
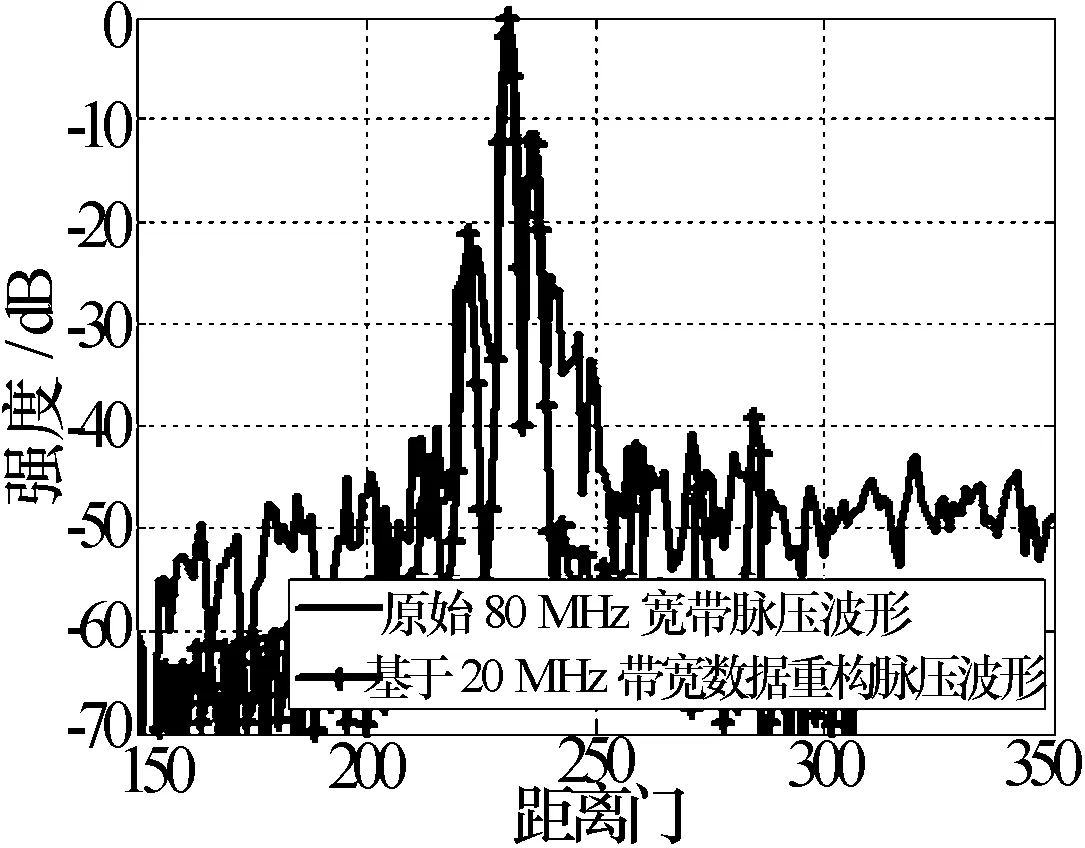
式中:向量v =[v(1),v(2), …,v(p), …,v(J)]是sinc(t)函数的采样向量,J h是稀疏的,Φv是h的观测矩阵,y为观测向量。那么,向量h的重构可以归结为如下问题 (12) 在一定条件下,式(12)和如下凸优化问题是等价的 (13) 由矩阵Φv的构造和文献[16-17]中的相关结论可知,式(12)和式(13)等价的条件是可以满足的。 考虑到噪声向量n,式(13)可进一步归结为如下问题求解 (14) 或 (15) 式中:η>0用来调整噪声和稀疏向量l0或l1范数之间的权重。对于噪声分量,采用l2范数。 进一步地,还可将式(15)转化为有约束优化问题 (16) 式中:ε表示噪声分量的影响。基于l1范数的凸优化算法或贪婪追踪系列算法可求解上述问题。 3仿真分析 3.1基于仿真数据的散射中心重构 仿真条件及参数设置: (1)散射点数N个; (2)虚拟采样间隔Δτ=Ts/10; (3)信号带宽1 MHz,脉宽30 μs; (4)散射点位置在观测向量y中随机确定,幅度服从高斯分布。 定义散射中心重构误差(dB) (17) 式中:h表示目标散射中心真实位置、幅度和相位;hconst表示重构位置、幅度和相位。 随机产生线性调频目标回波信号,散射点数目N=7,位置随机分布在7个超分辨距离单元内。对回波信号进行奈奎斯特采样,然后通过10内插(内插值为0)得到虚拟采样信号。一次随机仿真中,对虚拟采样信号进行脉压,脉压后波形如图3所示。为了更清晰表示本次仿真真实散射中心分布情况,图3同时给出了散射中心位置、幅度和相位信息。 图3 随机产生信号 基于图3a)中所示脉压波形和本文散射中心重构算法,重构脉压波形和散射中心与真实值的比较如图4所示。重构误差Er=-172 dB,即在无噪声情况下,本文算法几乎无失真重构出目标各散射中心。 图4 重构信号与真实信号的比较 散射中心数目分别为5、7、9、11、13、15时,每种情况进行20次仿真,重构平均误差如表1所示。 表1 不同散射点数目时散射中心重构平均误差 dB 从表1可以看出,多次仿真结果重构误差约在-170 dB量级,因此,基于式(16)可实现散射中心的正确重构。 3.2基于实录数据的散射中心重构 基于80 MHz带宽、100 MHz采样实录数据,仿真分析本文算法性能。为了更好地说明重构效果,将80 MHz宽带数据滤波成20 MHz带宽窄带数据,从滤波后的窄带数据中估计目标散射中心,然后基于散射中心估计结果重构80 MHz宽带脉压波形。将重构脉压波形与原始80 MHz带宽脉压波形进行对比,分析散射中心重构效果。信号处理过程如图5所示。 图5实录数据信号处理过程 80 MHz带宽回波及脉压后波形,如图6所示。 图6 80 MHz带宽信号 从80 MHz带宽脉压波形可以看出,该目标具有3到4个强散射中心。将80MHz带宽数据滤波成20 MHz,采样率不变,滤波后数据及脉压波形如图7所示。 图7 滤波后20 MHz带宽信号 滤波成20 MHz带宽数据,脉压后,目标平均SNR约为22.6 dB。由于距离分辨率降低4倍,脉压波形无法反映散射中心分布情况。但脉压波形中仍然包含散射中心分布信息,基于本文算法,目标散射中心重构结果如图8所示。 图8 基于20 MHz带宽数据散射中心重构结果 基于散射中心估计结果和基函数,重构脉压波形与真实波形的比较如图9所示。 图9 20 MHz重构脉压波形与真实波形的比较 为了验证基于20 MHz带宽数据的散射中心估计效果,利用80 MHz基函数和20 MHz带宽数据散射中心位置、幅度、相位估计结果,重构80 MHz脉压波形。重构波形与真实波形的比较如图10所示。 图10 基于20 MHz数据重构脉压波形与 从图8和图10重构结果可以看出,基于20 MHz带宽脉压波形,估计出目标3个强散射中心,与80 MHz宽带脉压波形所呈现的强散射点数和位置一致。定义如下脉压波形重构误差 Er=10lg (18) 式中:freal(t)表示真实脉压波形;fcontr(t)为重构脉压波形。结合图9和图10,统计SCNR>10 dB以上距离单元重构脉压波形误差,即215~245距离单元,重构宽带脉压波形误差约为-6.5 dB,当散射中心回波脉压后SCNR>15 dB时,可实现对散射中心的重构。 4结束语 在散射中心满足稀疏性条件下,研究了目标超分辨散射中心重构算法,该算法无需已知散射中心数目等先验信息。通过稀疏表示,本文算法将重构问题归结为凸优化问题,并利用仿真数据验证了问题解的正确性。基于实测数据分析结果表明,算法可重构出目标强散射中心,本文实验中,基于窄带20 MHz信号散射中心估计结果,恢复宽带80 MHz脉压波形,恢复误差约-6.5 dB,当SCNR>15 dB时可实现对散射中心重构。 参 考 文 献 [1]李青,李斌,胡文俊,等. 基于低分辨率雷达的海面舰船目标分类识别技术[J]. 现代雷达,2012,34(12):45-49. LI Qing, LI Bin, HU Wenjun, et al. Ship target classification based on the low bandwidth marine radar[J]. Modern Radar, 2012, 34(12): 45-49. [2]DAVID Blacknell, HUGH Griffiths. Radar automatic target recognition. The Institution of Engineering and Technology, London, 2013: 38-39. [3]马林. 雷达目标识别技术综述[J]. 现代雷达,2011,33(6):1-7. MA Lin. Review of radar automatic target recognition[J]. Modern Radar, 2011, 33(6): 1-7. [4]LI H J, WANG Y D, WANG L H. Mathcing score properties between range profiles of high-resolution radar targets[J]. IEEE transactions on Antennas and Propagation, 2001, 44(4):444-452. [5]MITCHELL R A, WESTERKAMP J J. Statistical feature based HRR radar classification[J]. Proceedings of the IEEE Aerospace and Electronics Conference, 1998, 44(4): 111-118. [6]LIAO X, RUNKLE P, CARIN L. Identification of ground targets from sequential high-range-resolution radar signatures[J]. IEEE Transactions on Aerospace & Electronic Systems, 2002, 38(4):1230-1240. [7]刘宏伟,杜兰,袁莉, 等. 雷达高分辨距离像目标识别研究进展[J]. 电子与信息学报,2005,27(8): 1328-1334. LIU Hongwei, DU Lan, Yuan Li, et al. Progress in radar automatic target recognition based on high range resolution profile[J]. Journal of Electronics & Information Technology, 2005, 27(8): 1328-1334. [8]CHUNDRAN V, ELGAR L S. Patern recognition using invariants defined from higher order spectra one-dimensional inputs[J]. IEEE Transactions on Signal Porcessing, 1993, 4 1(1):205-212. [9]KIM Y J, CHUNG J H. Signal bias removal based GMM for robust speaker recognition[C]// IEEE International Conference on Acoustics, Speech, and Signal Processing. [S.l.]: IEEE Press, 2002(4): 4163. [10]JOUNY I, GARBER E D, MOSES R L. Radar target identification using the bispectrum: a comparative study[J]. IEEE Transactions on Aerospace and Electronic Systems, 1995, 31(1): 69-77. [11]MAUD A R M, BELL M R. Sparse recovery and resolution of pulse-Doppler radar[C]// IEEE Radar Conference. [S.l.]: IEEE Press, 2014: 824-828. [12]DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306. [14]BARANIUK R G. Compressive sensing [Lecture Notes][J]. IEEE Signal Processing Magazine, 2007, 24(4): 118-121. [15]VAN den Berg E, FIEDLANDER M P. In pursuit of a root [J/OL]. [2013-3-21]. http://www.cs.ubc. ca/ ~mpf/ 2007-pursuit-of-a-root.html. [16]CANDES E J, WAKIN M B. An introduction to compressive sampling[J]. IEEE Signal Processing Magazine, 2008, 25(2): 21-30. [17]RAUHUT H. Compressive sensing and structured random matrices[J]. Radon, 2010(9): 1-92. Super-resolution Scattering Centers Estimation Based on Compressed Sensing JIN Benzhou,WU Gang (Nanjing Research Institute of Electronics Technology,Nanjing 210039, China) Abstract:Due to the requirement for feature extraction of scattering centers in radar target recognition, a method of super-resolution scattering center parameters estimation based on compressed sensing is proposed. By designing a dictionary, pulse compression signal is sparsely represented in this paper and then the CS framework is used to the reconstruction problem. Based on the simulation method, the correctness of our proposed scheme is verified. Through filtering a signal with 80 MHz bandwidth into a 20 MHz narrow-band signal, the super-resolution scattering centers are reconstructed by the 20 MHz signal and then wideband pulse compressed signal is recovered. Results show that the proposed algorithm is feasible to reconstruct scattering centers with an acceptable error. Key words:target recognition; compressed sensing; super-resolution; scattering centers 收稿日期:2015-07-22 修订日期:2015-09-20 通信作者:晋本周Email:jinbenzhou@126.com 中图分类号:TN97 文献标志码:A 文章编号:1004-7859(2015)12-0029-05