轴、横向荷载下微倾单桩地基反力法的解析解

张 磊，焦 丹

（1．西安建筑科技大学土木工程学院，陕西 西安 710055；2．西安建筑科技大学理学院，陕西 西安 710055）

桩基础既可以承受由上部结构和桩身自重等引起的轴向荷载，也可以同时承受风荷载、流水压力、车辆制动力和牵引力、离心力、船只或汽车的撞击力等水平荷载[1]．水平荷载使桩身产生侧向变形和内力，而轴向荷载使其进一步加大[2]，即P-△效应．横山幸满[3]给出了单层地基中地基反力系数为常数时，轴、横向荷载共同作用下半无限长桩侧向变形和内力的解析解．假定地基反力系数沿深度线性增加，张玲等[4]提出了层状地基中桩身侧向响应的幂级数解．张磊等[5]基于三参数形式的地基反力系数提出了半解析解．另外，姚文娟等[6]用有限杆单元法，Karthigeyan等[7]和郑刚等[8]用有限单元法，赵明华等[9]用试验的方法分别进行研究，并得到很多有益的结论．

上述研究[2-9]均认为荷载施加前桩身为竖直的，但工程中多种原因可使其存在初始微倾斜[10]：灌注桩在施工时，桩身可能因桩孔倾斜而倾斜；预制桩在施工时，桩身可能因垂直度控制不好而倾斜．陈荣保等[11]和NADEEM等[12]采用数值模拟、郑刚等[10]和CHAN等[13]通过模型试验及郑刚等[13]通过现场试验对微倾桩的竖向承载性状展开研究，但目前对轴、横向荷载共同作用下微倾桩水平承载性状的研究还很鲜见．赵明华等[15]通过室内模型试验研究了轴、横向荷载共同作用下微倾木桩的水平承载性状．赵明华等[16]提出了地基反力系数沿深度线性增加时的有限杆单元法，但桩身水平位移被预先假定为深度的三次幂函数．另外，对于超固结黏土和密砂，地基反力系数可取为常数[17-18]．

考虑桩身初始微倾斜，结合桩顶、底的边界条件，推导出地基反力系数为常数时轴、横向荷载共同作用下桩身侧向变形和内力的解析解，及桩身最大位移、最大弯矩及其所在位置的计算方法．采用Fortran语言编制了计算程序．通过与模型试验的实测结果进行对比来验证解及程序的可靠性，进一步分析了桩身初始微倾斜、轴向荷载等因素对桩身侧向响应的影响．

1 控制方程及解

1.1 方程的建立

如图1所示，一根桩上半段露出地面，下半段沉入土中．桩身存在初始倾斜，倾角为θ，其值远小于1，并以向右倾斜为正．桩顶作用水平力Qp、力矩Mp和轴向力Np．地面以上及以下桩长分别为H0和H1，并在各段上分别建立坐标系．假定自由段分布荷载：q(x)=q0+△qx/H0，式中q0和(q0+△q)分别为自由段桩身顶端及底端的分布荷载集度．分别为荷载作用下地面以上及以下桩身轴线的横坐标．令uG和u分别表示荷载作用下地面以上及以下桩身水平位移，则有

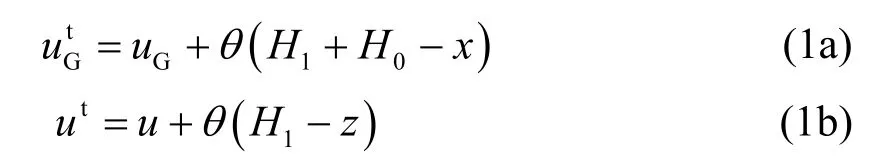
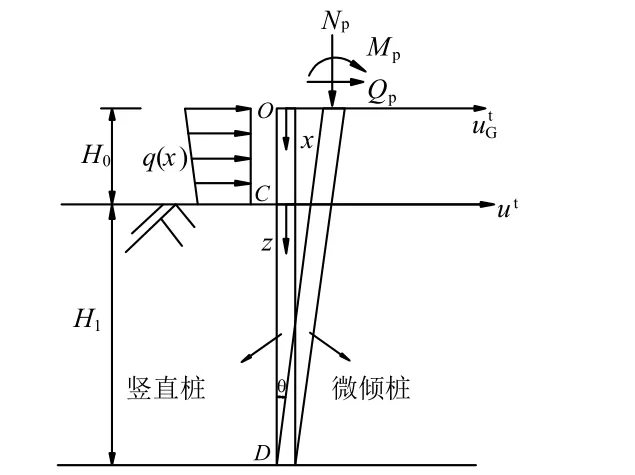
图1 轴、横向荷载下微倾单桩示意图Fig.1 Schematic diagram of a slightly inclined single pile under vertical and lateral loads

土体被离散成一系列独立的弹簧，且单位桩长上土反力p与桩身水平位移u成正比，即：p=kbu，式中：b为桩身宽度或直径；k为地基反力系数，假定为常数，适用于超固结黏土和密砂[17-18]．假定桩侧摩阻力和桩身自重对桩身侧向响应的影响很小，可忽略不计，也即桩身轴力等于施加于桩顶的轴向力Np，且满足：(大多数情况下适用[3])，式中EI为桩身抗弯刚度．

如图2所示，在地面以上桩身取一微元体进行受力分析，图中QG和MG分别为地面以上桩身的剪切力和弯矩．假定：位移以向右为正，转角以向左倾斜为正，弯矩以使桩身右侧受压为正，剪切力以绕研究对象顺时针转为正．

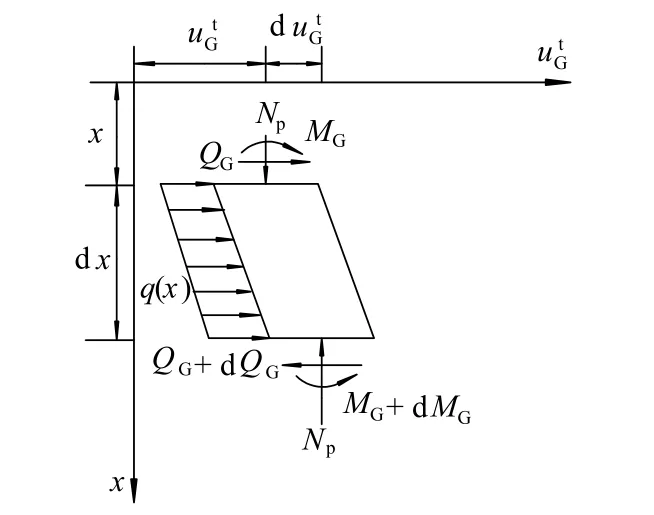
图2 地面以上桩身单元受力分析示意图Fig.2 Stress analysis of pile element above ground

由水平向力的平衡，并化简后得：

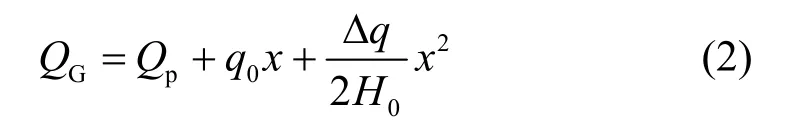
对下端点取矩，由力矩平衡，并略去高阶小量，化简后得：

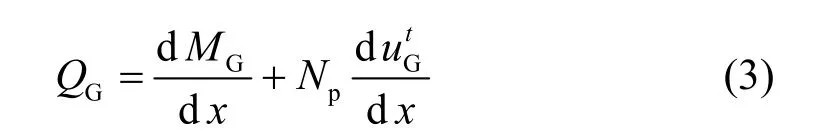
把式(1a)代入式(3)，化简后得：

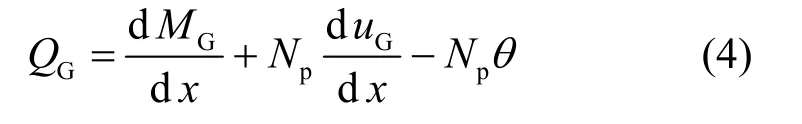
由欧拉—伯努利梁理论及式(1a)，得：

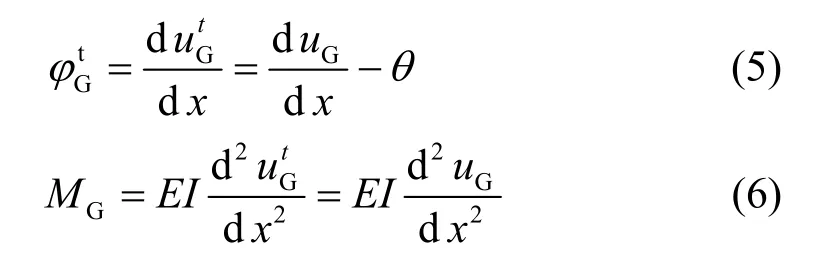
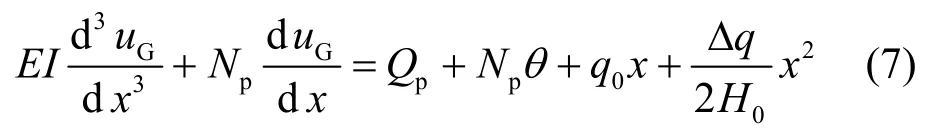
在地面以下桩身取一微元体进行受力分析，如图3所示，图中Q和M分别为地面以下桩身的剪切力和弯矩，并假定土反力以向左为正．

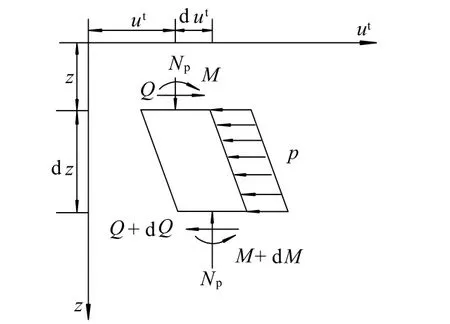
图3 地面以下桩身单元受力分析示意图Fig.3 Stress analysis of pile element under ground

由水平向力的平衡，并化简后得：

对下端点取矩，由力矩平衡，并略去高阶小量，化简后得：

把式(1b)代入式(9)，化简后得：

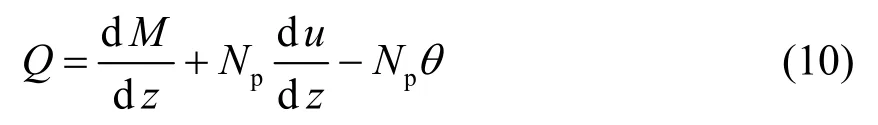
由欧拉—伯努利梁理论及式(1b)，得：

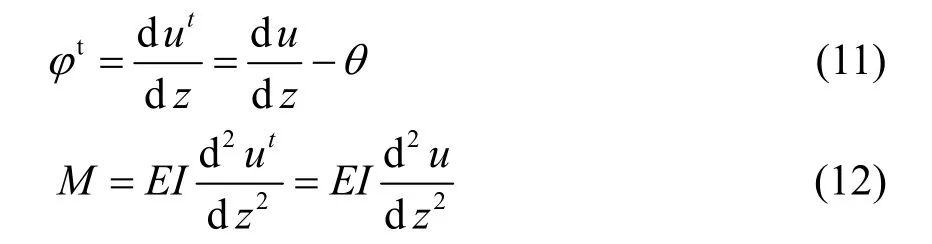
式中：tφ=φ-θ，为荷载作用下地面以下桩身轴线相对于纵坐标轴的转角，为荷载作用下地面以下桩身转角，所以：M为地面以下桩身弯矩．把式(12)代入式(10)，化简后得：

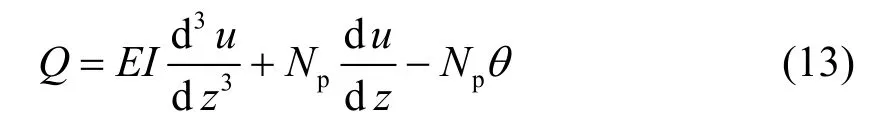
式(13)对z求导，并把式(8)代入，得地面以下桩身挠曲线微分方程：

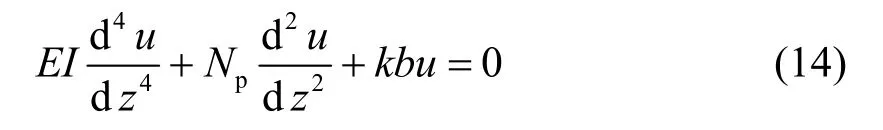
1.2 各桩段上的解

求解式(7)，得自由段桩身响应的解：

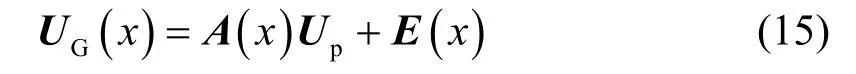
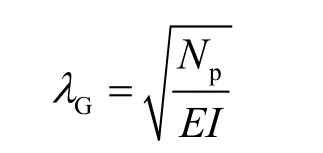
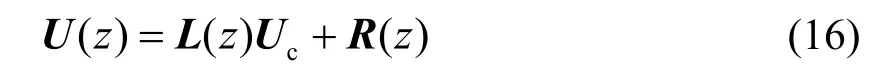
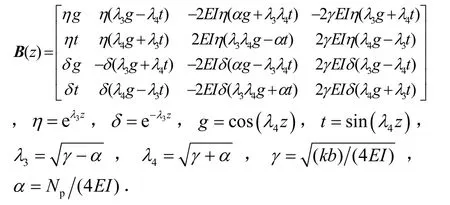
1.3 边界条件

当桩顶嵌入承台，在约束条件的限制下不能转动，只能在承台的带动下发生水平位移时，边界条件称为“桩顶固定”；当桩顶没有限制，可以在荷载的作用下自由的发生水平位移和转动时，边界条件称为“桩顶自由”．工程中桩顶的约束条件往往介于自由和固定之间．为求解方便，桩顶采用自由和固定两种理想化的情形．因此，桩顶自由时，Qp和Mp分别为桩顶施加的水平力和力矩荷载；桩顶固定时，p=0、Qp为桩顶施加的水平力．

当桩底嵌入基岩或硬土，在约束条件的限制下不能发生水平位移和转动时，边界条件称为“桩底固定”；当桩底嵌入基岩的深度不大或与基岩接触而只被限制发生水平位移时，边界条件称为“桩底铰接”；当桩底以下为软土时，边界条件称为“桩底自由”．因此，桩底自由时：M(H1)=0、Q(H1)=0；桩底铰接时：u(H1)=0、M(H1)=0；桩底固定时：u(H1)=0、(H1)=0．

1.4 求解过程

基于桩身响应在图1中C点处的连续性，及桩顶、底的边界条件，得桩顶未知的边界值：

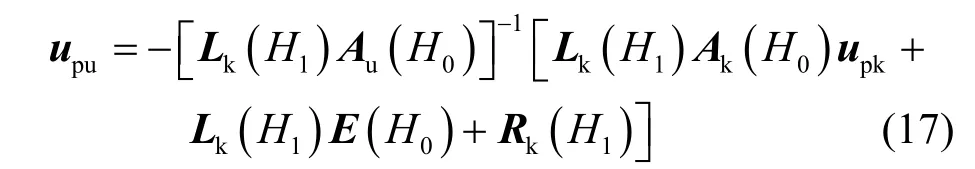
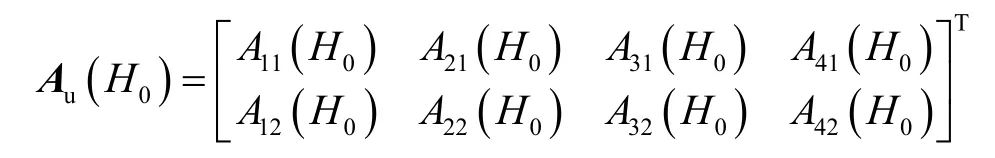
(式中：A11(H0)，A21(H0)…，A42(H0)取自矩阵如A32(H0)为矩阵A(H0)中第3行第2列的元素，下同)．

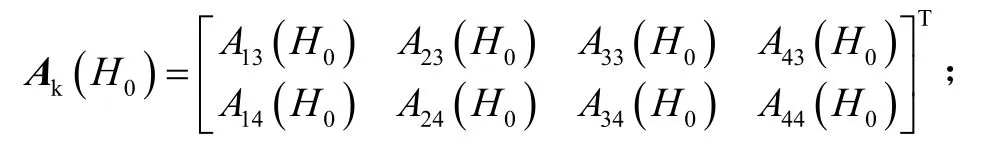
当桩顶固定时：

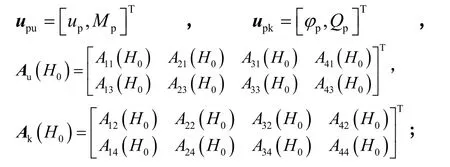
当桩底自由时：

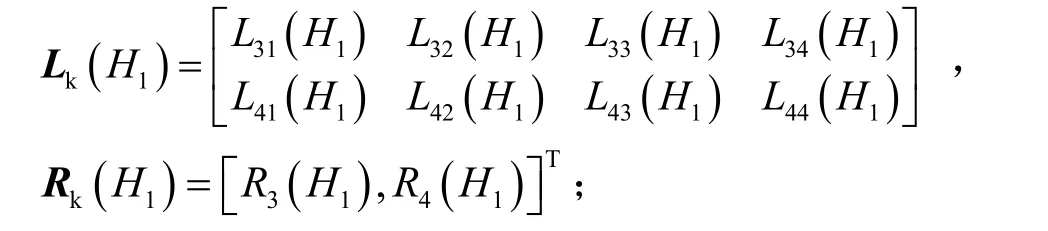
当桩底铰接时：

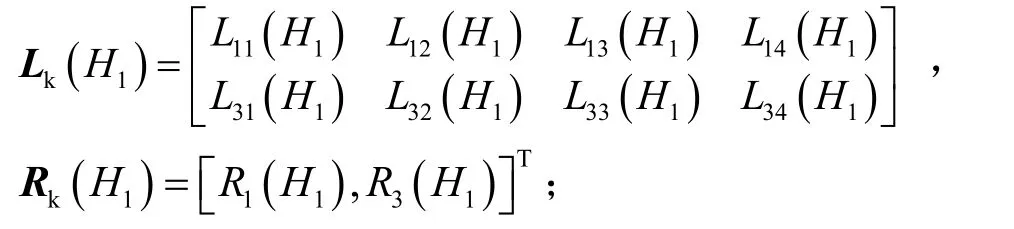
当桩底固定时：

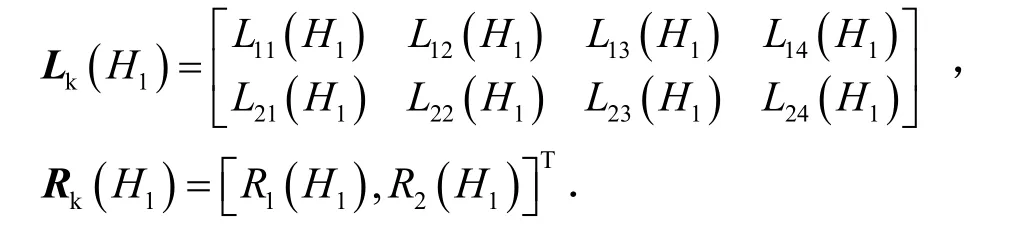
至此，桩顶的位移、转角、弯矩和剪切力全部已知．自由段桩身任意点处的变形和内力可通过式(15)得到．对于地面以下桩身任一点处的变形和内力，可先通过式(15)求得地面处桩身响应，然后由式(16)得所求点处桩身响应．对于层状地基，可类似式(16)先求得每一层任意点处桩身变形和内力与该层上分界点处桩身响应的关系，然后利用各层分界点处桩身响应的连续性，得桩顶及桩顶以下各点处桩身响应．

在水平承载桩基工程中，设计人员最关心的参数是桩身最大位移、最大弯矩及其所在位置．最大位移发生在桩顶；对于最大弯矩，可先采用二分法近似求得桩身弯矩的微分为零的点，然后比较该点弯矩和桩顶弯矩，以得到最大值．

2 算例验证

基于解采用Fortran语言编制了计算程序．以下将本文解的计算结果与模型试验的实测结果进行对比，以验证解及程序的可靠性．赵明华等[15]开展了3组轴、横向荷载共同作用下微倾木桩室内模型试验研究，其中02组第05号桩的桩径b=31.57 mm，自由段桩长H0=66.0 cm，地面以下桩长H1=69.0 cm，抗弯刚度EI=407.686 6 N·m2，桩身初始倾角θ=0．0129 rad，桩顶和桩底的边界条件均为自由．上覆黏土层厚30 cm，下卧砂土层厚70 cm．自由段桩身无分布荷载，地基反力系数k=4×104 kN/m3．桩、土其余参数详见文献[15]．水平力Qp=26.95 N、力矩Mp=0 N·m，地面处桩身水平位移的计算值及实测值与轴向荷载的关系如图4所示．

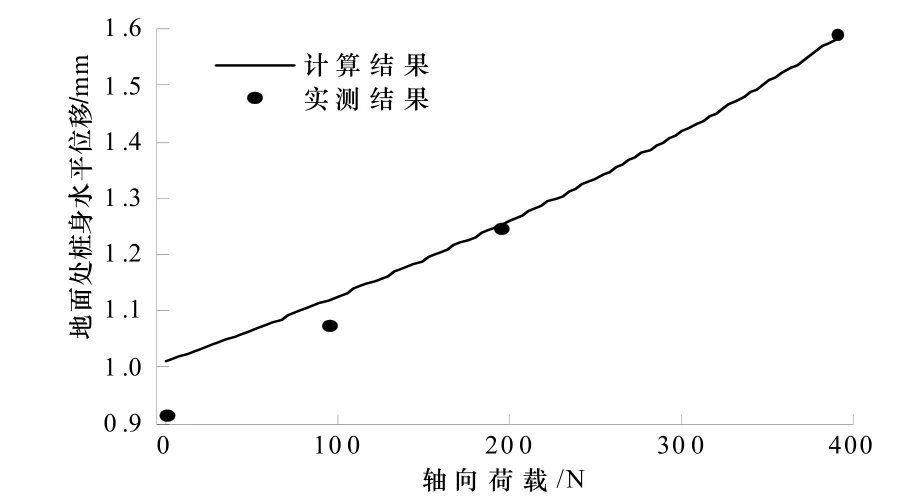
图4 计算结果与模型试验结果对比图Fig.4 Comparison between computed and test results

由图4可见，本文解计算结果与模型试验结果吻合度很高，说明所得解及程序是可靠的．

3 影响因素分析

为分析桩身初始微倾斜及轴向荷载等因素对桩身侧向响应的影响，另以某桥梁桩基为例分析如下．桩径b=1.8 m，自由段桩长H0=20 m，地面以下桩长H1=40 m，抗弯刚度EI=9.275×106 kN·m2，桩底固定，地基反力系数k=4×104 kN/m3，自由段无分布荷载．

3.1 桩身初始微倾斜的影响

轴向荷载Np=10 MN，不同的桩顶约束条件及不同的水平力和力矩荷载作用下，桩身最大位移、最大弯矩及桩身最大弯矩距离地面的距离与桩身初始倾角的关系如图5所示．

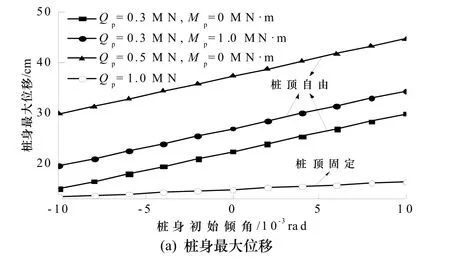
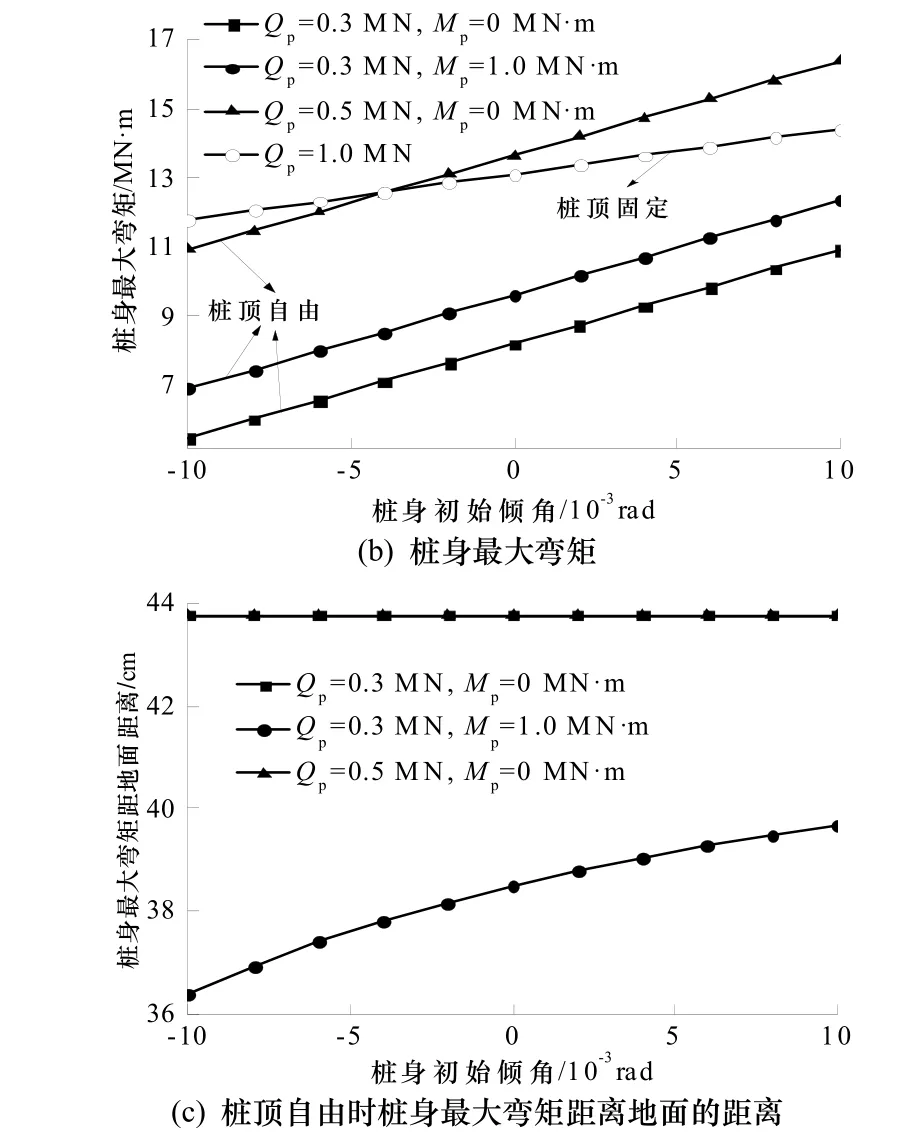
图5 桩身侧向响应与桩身初始倾角的关系Fig.5 Relationship between lateral pile responses and initial inclination angle of pile shaft

由图5(a)、(b)可见，桩顶自由时桩身最大位移和最大弯矩均随桩顶施加的水平力和力矩荷载的增加而增大．桩身最大位移和最大弯矩均随桩身初始倾角的增加而近似线性增大，且其变化速率随水平力和力矩荷载的增加而基本保持不变．由桩顶自由且Qp=0.3 MN、Mp=1 MN·m对应的曲线可知，当桩身初始倾角从0rad增加到1×10-2rad时，桩身最大位移和最大弯矩分别增加约27.7%和22．1%．桩顶固定时，桩身最大位移和最大弯矩也均随桩身初始倾角的增加而近似线性增大，但其变化速率比桩顶自由时小．由图5(c)可见，桩顶自由时，如果桩顶只承受水平力而不承受力矩荷载，水平力和桩身初始倾角对桩身最大弯矩距离地面的距离影响很小，可忽略不计；如果水平力和力矩荷载均较大，桩身最大弯矩距离地面的距离随桩身初始倾角的增加而增大，但其变化速率随桩身初始倾角的增加而逐渐减小．另外，计算结果显示桩顶固定时桩身最大弯矩位于桩顶．

3．2 轴向荷载的影响

水平力Qp=0.4 MN、力矩Mp=0.6 MN·m，桩顶自由，不同的桩身初始倾角下桩身最大位移、最大弯矩及桩身最大弯矩距离地面的距离与轴向荷载的关系如图6所示．由图6(a)、(b)可见，桩身最大位移和最大弯矩均随轴向荷载的增加而增大；其变化速率虽然在轴向荷载较小时较小，但随桩身初始倾角和轴向荷载的增加而增大．在曲线的后半段，桩身最大位移和最大弯矩随轴向荷载的增加而迅速增大，此时桩基已失稳．当轴向荷载为0 MN时，随着桩身初始倾角的增加，桩身最大位移和最大弯矩保持不变，这是因为本文中桩身初始微倾斜由施工等原因造成，倾角远小于1，属于小变形；对于工程中应用广泛的斜桩，桩身初始倾角较大，不在本文考虑之列．随着轴向荷载的增加，桩身初始微倾斜对桩身最大位移和最大弯矩的影响逐渐增大．由图6(c)可见，桩身最大弯矩距离地面的距离随轴向荷载的增加而近似线性减小．

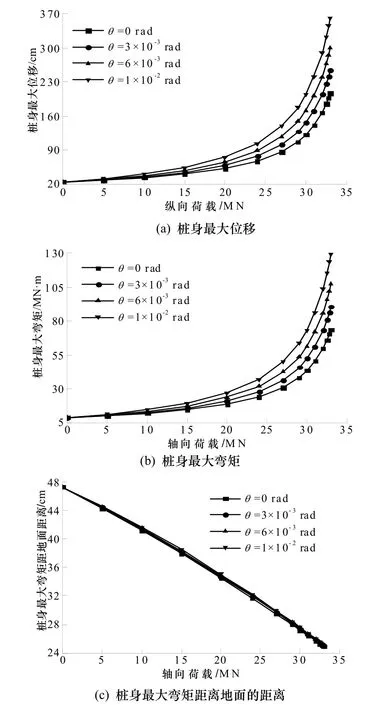
图6 桩身侧向响应与轴向荷载的关系Fig.6 Relationship between lateral pile responses and axial load

4 结论

考虑桩身初始微倾斜，提出了地基反力系数为常数时，轴、横向荷载共同作用下桩身侧向变形和内力的解析解，及桩身最大位移、最大弯矩及其所在位置的计算方法，编程计算后得如下主要结论：

(1) 桩身最大位移和最大弯矩均随桩顶施加的水平力和力矩荷载的增加而增大．

(2) 桩身最大位移和最大弯矩均随桩身初始倾角的增加而近似线性增大；其变化速率虽随轴向荷载的增加而增大，但基本不受水平力和力矩荷载的影响．桩顶自由时，如果桩顶只承受水平力而不承受力矩荷载，桩身最大弯矩距离地面的距离随水平力和桩身初始倾角的增加而基本保持不变；如果水平力和力矩荷载均较大，桩身最大弯矩距离地面的距离随桩身初始倾角的增加而增大，但其变化速率随桩身初始倾角的增加而逐渐减小．桩顶固定时，桩身最大弯矩位于桩顶．

(3) 桩身最大位移和最大弯矩均随轴向荷载的增加而增大，且其变化速率随桩身初始倾角和轴向荷载的增加而增大．轴向荷载可以引起桩基失稳．桩顶自由时桩身最大弯矩距离地面的距离随轴向荷载的增加而近似线性减小．

(4) 验证结果表明所得解及程序是可靠的．另外本文解适用于桩周为超固结黏土或密砂且桩身侧向变形不太大情况，在相关设计中可参考应用．

References

[1] 铁道部. 新建时速300～350公里客运专线铁路设计暂行规定：铁建设[2007]47号[S]. 北京: 中国铁道出版社,2008.Ministry of Railways. Interim provisions for newly built 300～350 km/h railway passenger-dedicated line: Railway Construction [2007] No.47 [S]. Beijing: China Railway Publishing House, 2008.

[2] LIANG F Y, CHEN H B, CHEN S L. Influences of axial load on the lateral response of single pile with integral equation method[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2012, 36(16):1831-1845.

[3] 横山幸满. 桩结构物的计算方法和计算实例[M]. 唐业清, 吴庆荪, 译. 北京:中国铁道出版社,1984.HENGSHAN X M. Computation methods and examples for pile structures[M]. TANG Yeqing, WU Qingsun,Translated. Beijing: China Railway Publishing House,1984.

[4] 张玲, 赵明华, 赵衡. 倾斜荷载下桩柱式桥墩受力变形分析传递矩阵法[J].中国公路学报,2015,28(2): 69-76.ZHANG Ling, ZHAO Minghua, ZHAO Heng. Transfer matrix method for deformation of pile type bridge pier under axial transverse load[J]. China Journal of Highway and Transport, 2015, 28(2): 69-76.

[5] 张磊, 龚晓南, 俞建霖. 纵横荷载下单桩地基反力法的半解析解[J]. 哈尔滨工业大学学报,2011,43(6):96- 100.ZHANG Lei, GONG Xiaonan, YU Jianlin. Semi-analytical solutions for single piles subjected to combined vertical and lateral loads by subgrade reaction method[J]. J. of Harbin Institute of Technology, 2011, 43(6): 96-100.

[6] 姚文娟, 吴怀睿, 程泽坤, 等. 基于 p-y曲线法的超长桩非线性数值分析[J].岩土工程学报,2011,33(11):1683-1690.YAO Wenjuan, WU Huairui, CHENG Zekun, et al. Nonlinear numerical analysis of super-long piles based on p-y curves[J]. Chinese Journal of Geotechnical Engineering,2011, 33(11): 1683-1690.

[7] KARTHIGEYAN S, RAMAKRISHNA V V G S T, RAJAGOPAL K. Numerical investigation of the effect of vertical load on the lateral response of piles[J]. Journal of Geotechnical and Geoenvironmental Engineering, ASCE,2007, 133(5): 512-521.

[8] 郑刚, 王丽. 成层土中倾斜荷载作用下桩承载力有限元分析[J]. 岩土力学, 2009, 30(3): 680-687.ZHENG Gang, WANG Li. Finite element analysis of bearing capacity of pile under inclined load in layered soil[J]. Rock and Soil Mechanics,2009,30(3):680-687.

[9] 赵明华, 吴鸣, 郭玉荣. 轴、横向荷载下桥梁基桩的受力分析及试验研究[J].中国公路学报,2002,15(1):50-54.ZHAO Minghua, WU Ming, GUO Yurong. Study of the behavior analysis and model test of bridge piles under simultaneous axial and lateral loading[J]. China Journal of Highway and Transport,2002, 15(1): 50-54.

[10] 郑刚, 李帅, 杜一鸣, 等. 竖向荷载作用下倾斜桩的承载力特性[J]. 天津大学学报, 2012, 45(7): 567-576.ZHENG Gang, LI Shuai, DU Yiming, et al. Bearing capacity behaviors of inclined pile under vertical load[J].Journal of Tianjin University, 2012, 45(7): 567-576.

[11] 陈荣保, 陆瑞明. 偏斜预应力管桩的承载力分析与处理[J]. 岩石力学与工程学报,2006,25(S2): 3545- 3551.CHEN Rongbao, LU Ruiming. Analysis and treatment of bearing capacity behavior of sloping prestressed pipepile[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(S2): 3545-3551.

[12] NADEEM M, CHAKRABORTY T, MATSAGAR V.Nonlinear buckling analysis of slender piles with geometric imperfections[J]. Journal of Geotechnical and Geoenvironmental Engineering, ASCE,2015, 141(1): 06014014.

[13] CHAN S F, HANNA T H. The loading ehavior of initially bent large scale laboratory piles in sand[J]. Canadian Geotechnical Journal, 1979, 16(1): 43-58.

[14] 郑刚, 王丽. 竖向荷载作用下倾斜桩的荷载传递性状及承载力研究[J]. 岩土工程学报, 2008, 30(3): 323-330.ZHENG Gang, WANG Li. Bearing capacity behaviors of inclined pile under vertical load[J]. Journal of Tianjin University, 2008, 30(3): 323-330.

[15] 赵明华, 李微哲, 杨明辉, 等. 成层地基中倾斜偏心荷载下基桩位移特性室内模型试验研究[J].土木工程学报, 2006, 39(12): 95-99.ZHAO Minghua, LI Weizhe, YANG Minghui, et al. A model test study on displacement of piles under inclined and eccentric loads in layered soils[J]. China Civil Engineering Journal, 2006, 39(12): 95-99.

[16] 赵明华, 李微哲, 单远铭, 等. 成层地基中倾斜荷载桩改进有限杆单元法研究[J].工程力学,2008,25(5):79-84.ZHAO Minghua, LI Weizhe, SHAN Yuanming, et al.Behavior analysis of piles in layered clays under eccentric and inclined loads by improved finite pole element method[J]. Engineering Mechanics, 2008, 25(5): 79-84.

[17] HSIUNG Y M. Theoretical elastic-plastic solution for laterally loaded piles[J]. Journal of Geotechnical and Geoenvironmetal Engineering, 2003, 129(5): 475-480.

[18] GUO W D. Nonlinear response of laterally loaded piles and pile groups[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2009, 33(7):879-914.