无线传感器网络中DV-Hop定位算法的改进*
2016-01-21马淑丽赵建平
马淑丽,赵建平
(曲阜师范大学 物理工程学院,山东 曲阜 273165 )
无线传感器网络中DV-Hop定位算法的改进*
马淑丽,赵建平
(曲阜师范大学 物理工程学院,山东 曲阜 273165 )
Foundation Item: National Natural Science Foundation of China(No.11302118);Science and Technology Project of Higher Education of Shandong Province(No.J12LN08)
摘要:无线传感器网络中基于无需测距的节点定位算法定位精度不高,一般应用在粗精度定位中。为了提高基于无需测距的DV-Hop算法定位精度,利用最小均方差准则改进算法,通过修改指数值精化平均每一跳距离,提出不同通信半径、不同锚节点覆盖率下的最佳指数值概念,并应用在一种锚节点均匀分布环境中,进一步提高定位精度。MTLAB仿真结果表明,在最佳指数值下,改进的算法在不同锚节点覆盖率、不同通信半径下能提高定位精度,同时不会增加节点能量消耗与硬件成本。
关键词:无线传感器网络;节点定位;DV-Hop;最小均方差;节点分布
0引言
无线传感器网络(Wireless Sensor Network,WSN)由大量传感器节点组成,可执行目标识别、环境监测、信息采集、定位跟踪等任务。应用范围广泛,可应用在需要测量各种物理量(如温度、湿度、辐射、酸度、振动等)的军事、矿山井下定位、农业、环境监测等领域。无线传感器网络的关键技术有节点定位、路由协议、安全保密[1]等。节点定位的算法实现主要有两类[2]:一类是高成本、高定位精度的基于测距的算法;另一类是使用低成本、低定位精度的无需测距的定位算法。无需测距算法广泛应用在粗精度定位的应用中[3]。
节点定位的研究主要考虑定位精度、网络成本、节点能量消耗、计算量等。定位精度在一般粗精度定位应用中达到0.4以下即可满足应用[3]。网络成本主要考虑物理区域中节点总数、锚节点覆盖率。锚节点因装有导航设备成本一般比普通节点高两个数量级[4],所以应用中锚节点所占比例一般控制在15%左右。节点由单独电源供电,能量消耗受泛洪次数、通信半径、传输数据量等影响。节点电量耗尽后死亡,整个网络生命周期下降。另外,网络连通度过大也会增加网络成本或节点能耗。
现有的文献一般只考虑提高定位精度、降低计算量等方面,其他方面没有充分考虑。如文献[5]利用节点间的覆盖率改进算法,提高了定位精度,但是通信半径和网络中节点数取值过大,使网络连通度达到308,定位精度在0.4以上,不能满足一般的实际应用。文献[6]设定的仿真环境中节点密度较大,增加了网络成本。文献[7]节点通信半径取值过高,网络连通度达到201,会影响网络成本与节点能量消耗。文献[8]中设定锚节点覆盖率从10%到90%,成本过高,不符合实际应用。文献[9]提出的 DV-Hop(A)算法用最小均方误差准则来计算平均每跳距离,提高了定位精度,但是其网络连通度最高达113.1,锚节点覆盖率从30%到90%,很不合理。本文充分考虑并确保节点定位精度0.4以下、锚节点覆盖率16%以内、节点通信半径43 m以下、网络连通度控制在58以下,在不增加硬件设备和节点能量消耗下,改进算法,提高了定位精度,并应用在一种均匀的锚节点分布环境,使定位精度进一步提高。
1典型DV-Hop定位算法概述
1.1DV-Hop算法
DV-Hop定位算法由美国罗格斯大学(Rutgers University)Dragos Niculescu等人提出。DV-Hop算法利用多跳锚节点信息定位。当未知节点获得与至少3个锚节点的距离时,可用三边测量法、极大似然法等求出节点坐标。
假设前提:在无线传感器网络区域内,有少数自带导航装置或自身位置信息已知的锚节点(有的文献称为信标节点),有大量未知节点随机分布。每个节点都有自己的编号和相同的通信半径,可以与其通信半径内的其他节点实现双通信。
定位过程:首先锚节点以泛洪的方式向网络广播自身位置信息和初始跳数值0,节点接收到信息后将跳数值加1并转播出去。转播过程中,节点只保留与其他节点间的最小跳数值。根据锚节点间的跳数与实际距离可得到每个锚节点的平均每跳距离。利用跳数乘以锚节点的平均每跳距离得到未知节点与锚节点的估算距离,其过程有两种方法:一般方法是,未知节点只接收离自己最近的锚节点的平均每跳距离并作为计算与所有锚节点估算距离时的平均每跳距离。另一种方法是,文献[9]提出的计算未知节点与锚节点的距离时采用相应的锚节点的平均每跳距离。经试验发现后一种方法对提升定位精度没有多大意义,本文采用前一种方法。
得到未知节点与锚节点的估算距离后,用极大似然法计算节点坐标过程:
(1)
AX=b
(2)
(3)
(4)
(5)
式中,di是未知节点与锚节点i间的估算距离,x,y是未知节点真实坐标值,xi,yi是锚节点i坐标值,n是锚节点个数。
1.2相关概念
节点定位算法中,绝对误差指未知节点i的定位坐标(xi,yi)与实际坐标(x0i,y0i)的距离,一般作为节点i的定位误差,计算如式(6):
(6)
定位精度指网络中全部节点(N个)的平均定位误差与节点通信半径R的比率,值越小定位精度越高,计算如式(7):
(7)
二维网络连通度C由网络区域边长L、网络中节点总数N,节点通信半径R决定,计算如式(8):
(8)
锚节点覆盖率指网络中锚节点个数占全部节点的比率。
2DV-Hop定位算法的改进与应用环境
2.1DV-Hop算法的改进
DV-Hop算法根据无偏估计准则计算平均每跳距离,需满足下式:
(9)
从而得出:
(10)
式中,dHopi是锚节点i到其他锚节点的平均每一跳距离。dij是锚节点i、j间的距离。hij是锚节点i、j间的最小跳数。xi,yi是锚节点i坐标值,xj,yj是锚节点j坐标值。
如图1所示,网络中分布着 A、B、C三个锚节点,其他为未知节点。
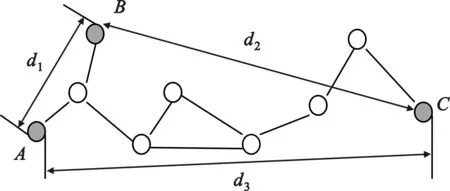
图1 网络结构
则由式(10)得:dHopA=(d1+d2)/(2+6),从图1看出,计算的锚节点A的平均每跳距离要小于实际平均每跳距离,计算误差较大。
文献[9]提出DV-Hop(A)算法,基于最小均方误差准则计算平均每跳距离,满足下式:
(11)
式中,m为锚节点个数,对函数f求关于的dHopi偏导并取零,得到最小均方误差下的平均每跳距离公式:
(12)
由式(12)得:dHopA=(2d1+6d2)/(22+62),文献[9]在式(12)中分母hij的指数取为2,经仿真其提出的改进算法能在较小的通信半径范围下提高节点定位精度,缺点是当通信半径增大时提高的定位精度下降。
本文改进式(12)中分母hij的指数,精化锚节点i的平均每一跳距离dHopi,如式(13)。将指数值α取为1.9到2.0之间的数,提出在不同锚节点覆盖率和不同通信半径下各自对应最佳指数值。经仿真发现指数值α取1.9~2.0的最佳指数值时,定位精度比文献[9]提出的DV-Hop(A)算法高。通信半径增大时,本文算法仍能明显的提升定位精度。
(13)
2.2应用环境
许多文献,如文献[2]采用节点随机均匀分布环境。文献[10-13]分别提出了4种锚节点均匀分布环境,提高了DV-Hop算法定位精度,其中文献[13]分布环境提高的定位精度最高。本文采用文献[13]提出的环境:将正方形区域划分为16个大小相同的小正方形,每个小正方形几何中心放置1个锚节点,其他未知节点随机分布,如图2所示。文献[2]随机均匀分布的仿真环境如图3所示。
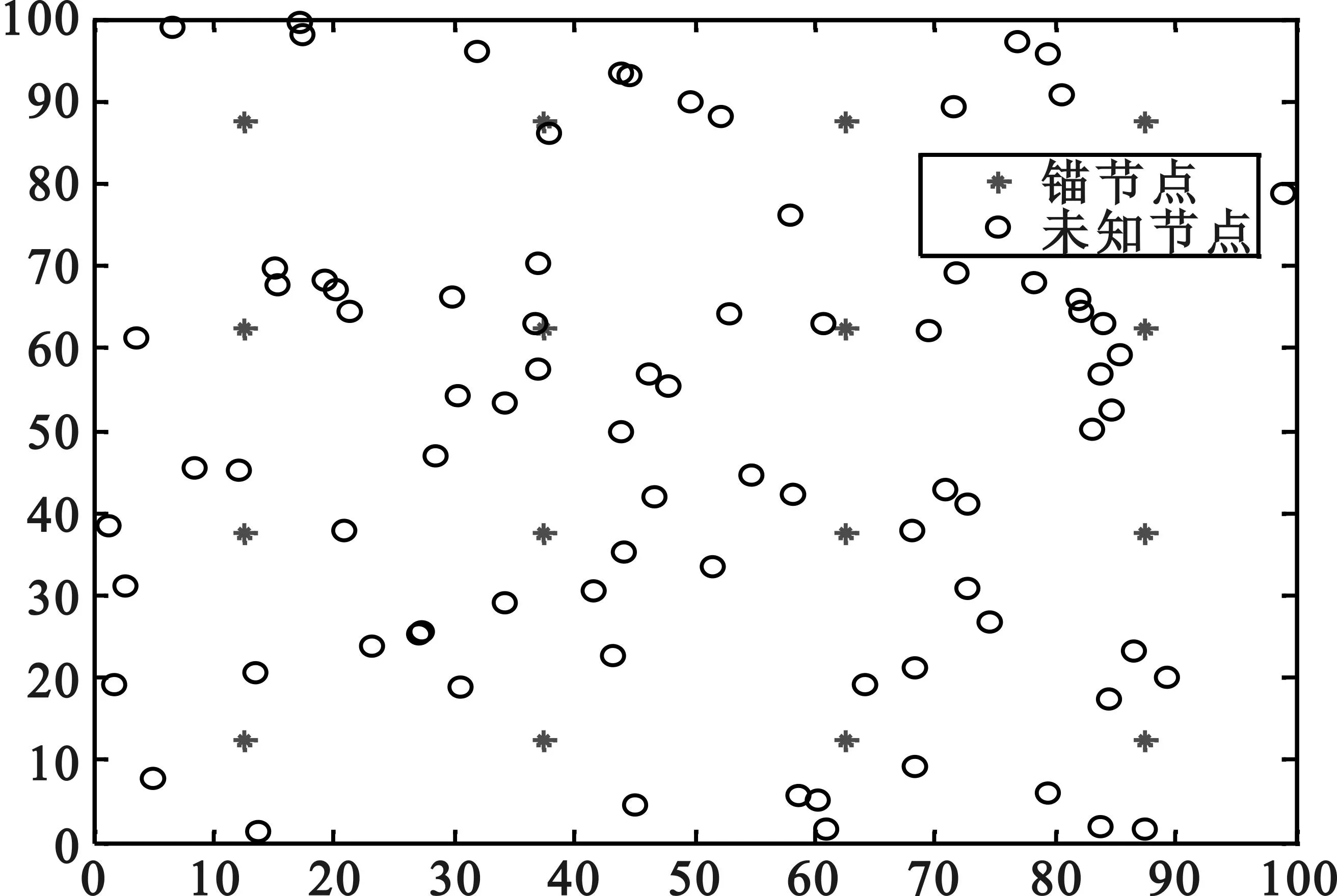
图2 文献[13]节点分布环境
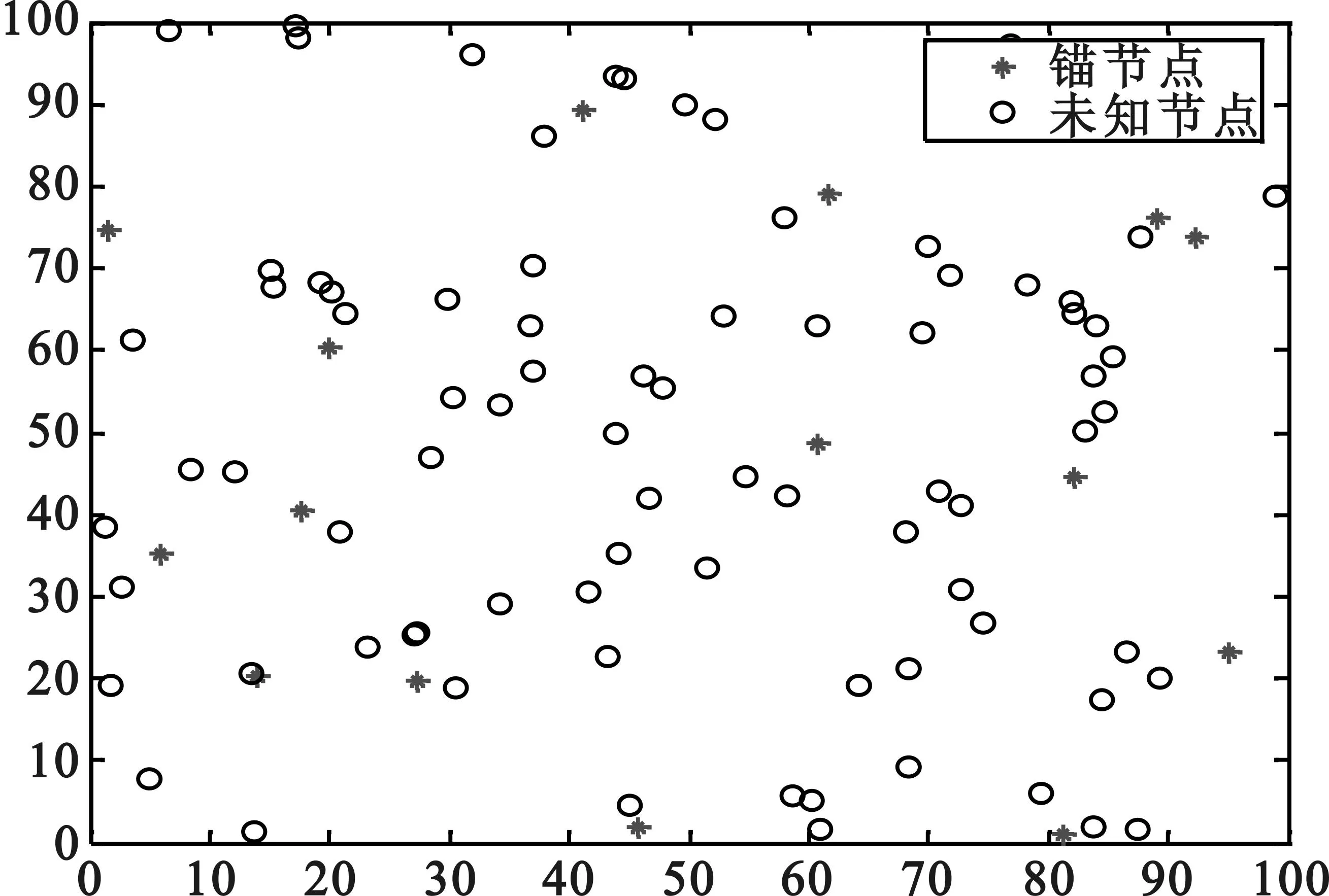
图3 文献[2]节点分布环境
3仿真结果分析
3.1求不同通信半径的最佳指数值
在边长100 m的正方形区域,按文献[2]节点分布环境布置100个节点,其中16个锚节点,通信半径取28、31、34、37、40、43 m,α取1.90、1.91、1.92、1.93、1.94、1.95、1.96、1.97、1.98、1.99、2.00。将本文算法与DV-Hop算法对比。由于节点分布随机性,仿真100次取平均值,如图4所示。
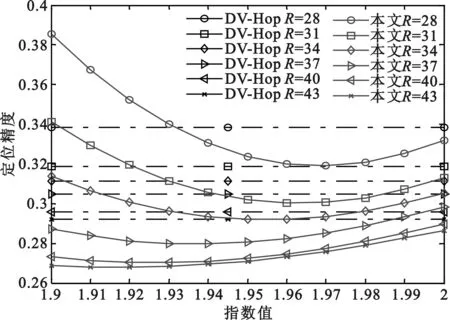
图4两种算法对比
从图4得出,锚节点覆盖率16%时,本文算法在不同的通信半径下对应不同的最佳指数值。通信半径为28、31、34、37、40、43 m时最佳指数值分别为1.97、1.96、1.95、1.94、1.93、1.92。在上述6个通信半径下取最佳指数值时本文算法比DV-Hop(A)算法定位精度分别提高1.27%、1.27%、1.33%、1.88%、1.96%、1.87%,比DV-Hop算法分别提高1.92%、1.86%、1.93%、2.5%、2.54%、2.42%。随着通信半径增大,本文算法比DV-Hop(A)算法更能明显的提升定位精度。
3.2求不同锚节点覆盖率的最佳指数值
将锚节点覆盖率取8%、10%、12%、14%、15%、16%,通信半径取43 m。仿真100次,如图5所示。
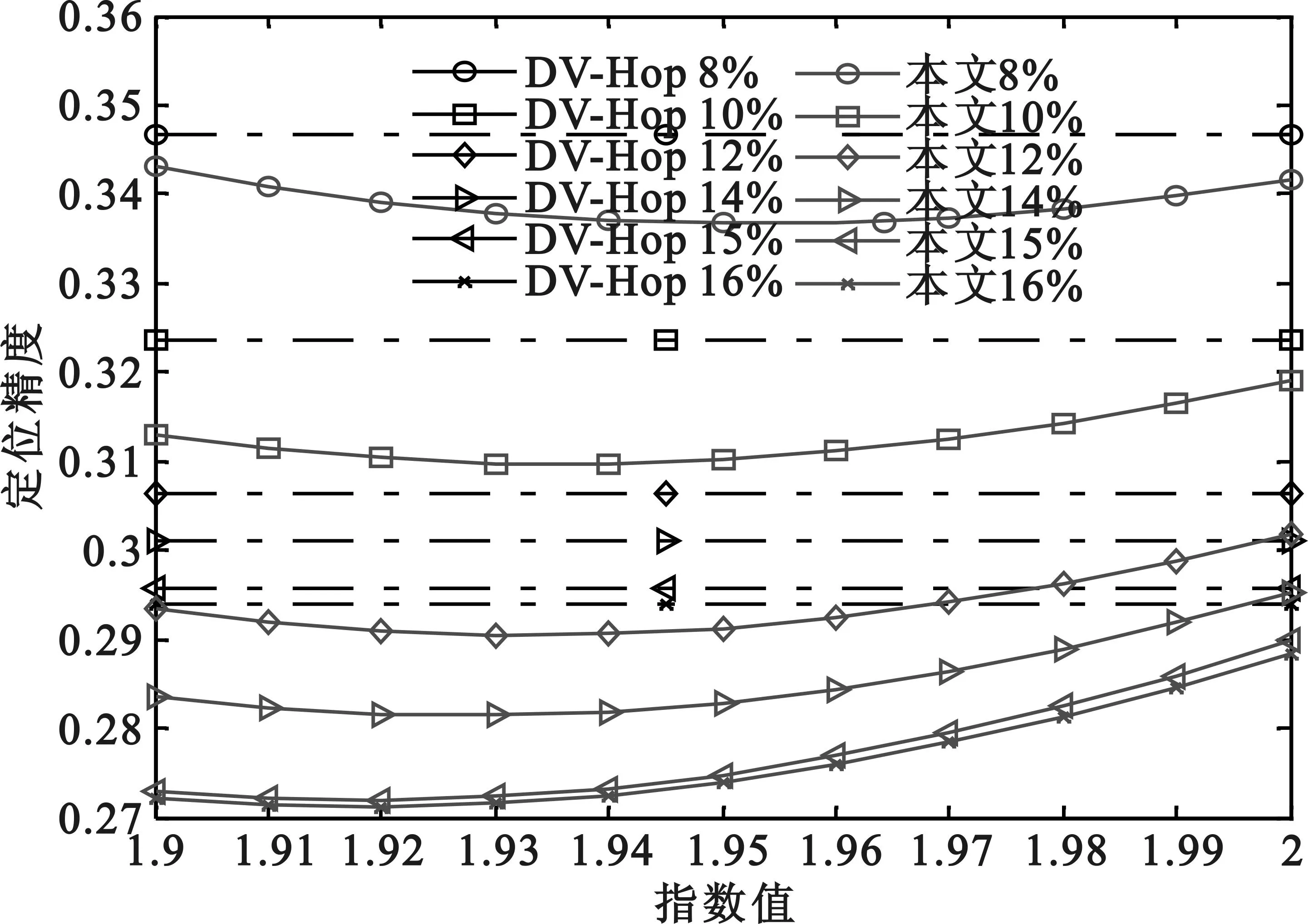
图5 两种算法对比
从图5得出,通信半径43 m时,本文算法在不同的锚节点覆盖率下对应不同的最佳指数值。锚节点覆盖率为8%、10%、12%、14%、15%、16%时最佳指数值分别为1.95、1.93、1.93、1.93、1.92、1.92。在上述6个锚节点覆盖率下取最佳指数值时,本文算法比DV-Hop(A)算法定位精度分别提高0.5%、0.92%、1.13%、1.38%、1.79%、1.71%,比DV-Hop算法分别提高0.99%、1.39%、1.59%、1.96%、2.39%、2.28%。
3.3本文算法在文献[13]环境中的应用
在区域内按照文献[13]提出的节点分布环境,放置16个锚节点和84个未知节点。通信半径取28、30、32、34、36、38、40、42 m,α值取1.90、1.92、1.94、1.96、1.98。分别在文献[2、13]随机分布环境下仿真本文算法。运行100次,如图6所示。
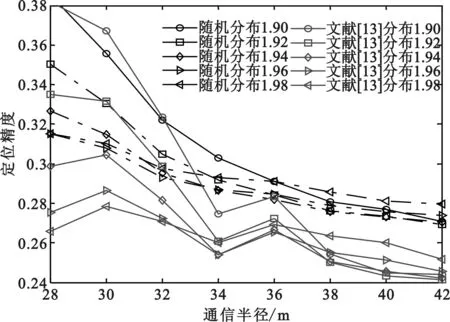
图6 本文算法在两种环境下对比
图6中,8个通信半径分别取其对应的最佳指数值时,本文算法在文献[13]环境下比在文献[2]随机分布环境下定位精度分别提高4.93%、2.95%、2.19%、3.24%、1.64%、2.55%、2.99%、2.78%。说明本文算法在文献[13]环境下应用,更能提高定位精度,缺点是节点的布置增加了人力负担。
3.4三种算法分别在文献[2、13]环境下的对比
锚节点覆盖率取16%,通信半径取26、28、30、32、34、36、38、40、42、43 m。本文算法取在两种环境中相应通信半径下的最佳指数值,与DV-Hop算法、DV-Hop(A)算法分别在文献[2、13]随机分布环境下仿真。运行100次,如图7所示。
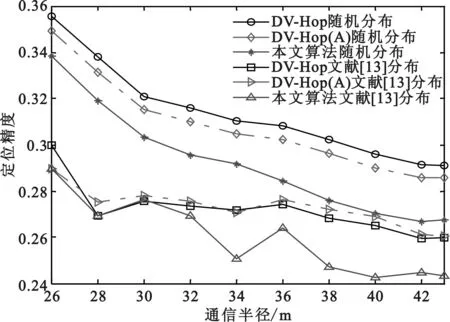
图7两种环境下DV-Hop、DV-Hop(A)、本文算法对比
由图7得,本文算法在相同的环境下比DV-Hop算法、DV-Hop(A)算法定位精度高。通信半径为26、34 m时,本文算法在文献[13]环境定位精度比DV-Hop算法在文献[2]随机分布环境下分别提高6.57%、5.96%,比DV-Hop(A)定位法分别提高5.97%、5.38%。
4结语
本文利用最小均方差准则改进文献[9]提出的DV-Hop(A)算法,修改指数值,提出最佳指数值概念。在不同的通信半径及锚节点覆盖率下分别取最佳的指数值时,本文算法可以提高节点定位精度2%左右,又结合文献[13]提出的锚节点均匀分布环境,进一步提高定位精度6%左右。随着通信半径增大,本文算法比文献[9]DV-Hop(A)算法更能提升节点定位精度。锚节点覆盖率为16%时,提出的节点定位方法比一般DV-Hop定位方法提高定位精度6%左右,比DV-Hop(A)方法提高5%左右。下一步将进一步改进算法提高定位精度。
参考文献:
[1](德)达尔吉,(美)玻尔拉伯尔.无线传感器网络基础理与实践[M].孙利民等译.清华大学出版社,2014.
(Germany) Dargie W,(America) Poellabaure C. The Wireless Sensor Network Basic Theory and Practice [M]. SUN M L Translation. Tsinghua University Press, 2014.
[2]林金朝,李小玲,刘海波.无线传感器网络DV-Hop算法改进与性能[J].重庆大学学报,2010,33(02):127-132.
LIN Jin-chao, LI Xiao-ling, LIU Hai-bo. Improvement and Performances of DV-Hop Localization Algorithm in Wireless Sensor Networks[J].Journal of Chongqing University,2010,33(02):127-132.
[3]周正.无线传感器网络的节点自定位技术[J].中兴通信技术,2005,11(04):51-56.
ZHOU Zheng. Self-Localization Technologies for Wireless Sensor Network Nodes[J].ZTE Communications, 2005, 11 (04): 51-56.
[4]姚向华,杨新宇,易劲刚等.无线传感器网络原理与应用[M].北京:高等教育出版社,2012.
YAO Xiang-hua, YANG Xin-yu, YI Jin-gang, et al. Wireless Sensor Network Principle and Application [M]. Beijing: Higher Education Press, 2012.
[5]谭志,张卉.基于节点间覆盖关系的改进DV-Hop算法[J]. 北京邮电大学学报, 2014, 37(01):35-38.
TAN Zhi, ZHANG Hui. Improved DV-Hop Localization Algorithm based on Coverage of Nodes[J]. Journal of Beijing University of Posts and Telecommunications,2014,37 (01):35-38.
[6]吴玉成,李江雯.基于最优节点通信半径的改进DV-Hop定位算法[J]. 华南理工大学学报:自然科学版,2012,40(06):37-42.
WU Yu-cheng, LI Jiang-wen.Improved DV-Hop Localization Algorithm based on Optimal Communication Radius of Nodes [J].Journal of South China University of Technology (Natural Science Edition),2012,40 (06):37-42.
[7]申铉京,李成岳,王硕.基于最优锚节点的无线传感器网络节点定位算法[J].吉林大学学报:工学版,2011,41 (S1):208-214.
SHEN Xuan-jing, LI Cheng-yue, WANG Shuo. Localization Algorithm based on Optimal Nodes for Wireless Sensor Networks[J]. Journal of Jilin University (Engineering and Technology Edition),2011,41 (S1):208-214.
[8]郑吉平,张永平,赵国安. 基于节点间连通性差异的DV-Hop定位算法[J].北京邮电大学学报,2012,35 (06):44-49.
ZHENG Ji-ping, ZHANG Yong-ping, ZHAO Guo-an. A Novel DV-Hop Localization Algorithm based on the Connectivity Differences of Sensor Nodes[J]. Journal of Beijing University of Posts and Telecommunications,2012, 35 (06 ):44-49.
[9]嵇玮玮,刘中.DV-Hop定位算法在随机传感器网络中的应用研究[J].电子与信息学报,2008,30(04):970-974.
JI Wei-wei,LIU Zhong.Study on the Application of DV-Hop Localization Algorithms to Random Sensor Networks[J]. Journal of Electronics & Information Technology, 2008,30(4):970-974.
[10]宫娜娜,武海艳.传感器网络节点分布均匀性与定位性能的关系[J].电子测量技术,2014,37(12):80-85.
GONG Na-na,WU Hai-yang. The Relationship Between the Sensor Network Node Distribution Uniformity and Positioning Performance[J]. Electronic Measurement Technology,2014,37(12):80-85.
[11]黄炎炎,陈向东,倪进权等.改进的DV-HOP无线传感器网络定位算法[J].通信技术,2014, 47(07): 765-769.
HUANG Yan-yan,CHEN Xiang-dong,NI Jin-quan,et al. An Improved DV-Hop Localization Algorithm for Wireless Sensor Networks[J]. Communications Technology, 2014, 47(7):765-769.
[12]ZHENG You-si, WAN Lei, SUN Zhi,et al.A Long Range DV-Hop Localization Algorithm with Placement Strategy in Wireless Sensor Networks[C] // Wireless Communications, Networking and Mobile Computing,2008. WiCOM'08.4thInternational Conference on.[s.l.]: IEEE, 2008: 1-5.
[13]马淑丽,赵建平,张炳婷.WSN中节点定位方法的改进[J].通信技术,2015,48(04):453-457.
MA Shu-li,ZHAO Jian-ping,ZHANG Bing-ting. Improvement of Node Locating Algorithm in WSN[J].Communications Technology, 2015, 48(04):453-457.

马淑丽(1989—),女,硕士研究生,主要研究方向为无线传感器网络、无线通信技术;
赵建平(1964—),男,教授,主要研究方向为无线通信技术。
Improvement of DV-HOP Algorithm in Wireless Sensor Networks
MA Shu-li,ZHAO Jian-ping
(College of Physics Engineering ,Qufu Normal University , Qufu Shandon 273165,China )
Abstract:The range-free node localization algorithm, for its not so high positioning accuracy in the wireless sensor network, and is usually applied in coarse-precision positioning. In order to improve the precision of range-free DV-Hop positioning algorithm, the least mean square error criterion method is used to modify the index for refining the value of average hop distance. Thus the concept of optimal index under different communication radius and different anchor nodes number is proposed, and by combining with a uniform distribution of anchor nodes, the positioning accuracy is further improved. Simulation with MTLAB indicates that, with the optimal value of index, the algorithm could improve the location accuracy in different anchor nodes coverage rates and in the different communication radius, without any increase of node energy consumption and hardware cost.
Key words:wireless sensor network; node location; DV-Hop; least mean square error criterion; nodes distribution
作者简介:
中图分类号:TP393
文献标志码:A
文章编号:1002-0802(2015)07-0840-05
基金项目:国家自然科学基金资助项目(No.11302118);山东省高等学校科技计划项目资助(No.J12LN08)
收稿日期:修回日期:2015-05-10Received date:2015-02-09;Revised date:2015-05-10
doi:10.3969/j.issn.1002-0802.2015.07.018
