一种1090ES相位编码信号的同步算法*
2016-01-21何东林黄忠涛孙清清
宋 妍,王 洪,何东林,黄忠涛,孙清清
(1.电子科技大学,四川 成都 611731;2.中国民用航空局第二研究所,四川 成都 610041)
一种1090ES相位编码信号的同步算法*
宋妍1,王洪1,何东林2,黄忠涛2,孙清清1
(1.电子科技大学,四川 成都 611731;2.中国民用航空局第二研究所,四川 成都 610041)
Foundation Item:Key Project of National Natural Science Foundation of China(No.61139003)
摘要:载波同步是对1090MHz扩展电文(1090MHz Extended Squitter,1090ES)的相位编码信号进行相干解调的前提和基础,研究针对这种调制方式的基于数据辅助的载波频偏估计算法。构建了1090ES相位编码信号的频偏估计模型,提出了一种基于遗传算法的频偏估计算法,详述了该算法的特点及其实现步骤,并通过MATLAB仿真,分析比较了该算法与Kay算法、Fitz算法及M&M算法的频偏估计性能。该算法的频偏估计范围可以达到采样频率的50%,在信噪比高于3 dB时,频偏估计的均方误差接近于修正的克拉美罗界,并且可以同时兼顾频偏估计精度和频偏估计范围。
关键词:1090ES;频偏估计;数据辅助;遗传算法
0引言
广播式自动相关监视(Automatic Dependent Surveillance-Broadcast, ADS-B)是利用空-地、空-空数据通信完成交通监视和信息传递的一种航空新技术,被国际民航组织(International Civil Aviation Organization, ICAO)确定为未来监视技术发展的主要方向,已在美国、澳大利亚等一些国家投入使用。1090ES是ICAO推荐的全球可互用的ADS-B广播数据链,其下行链路的应答载频是1 090 MHz,信息数据采用脉冲位置调制(Pulse Position Modulation, PPM)编码[1],每个消息单元包含8 μs前导脉冲和112 bits数据块,除去24 bits校验位,ADS-B消息的实际有效信息位长度为88 bits。此外,除了ADS-B 1090ES外,使用1 090 MHz频段的航空设备还包括S模式二次雷达、空中交通管制雷达信标系统及机载防撞系统等,致使1 090 MHz频段出现频谱拥挤状况,从而,ICAO附件10中明文规定将ADS-B系统的消息更新频率限制在6.2次/秒之内[2],因此现有1090ES ADS-B系统的数据通信容量最大仅为545.6 bits/s。由此,国际航空无线电技术委员会提出扩展1090ES数据链容量,ICAO提出的对1090ES信号中的PPM信息进行相位调制的扩容技术[3]具有重要研究意义,该项扩容技术正在美国联邦航空管理局及欧洲航管组织中进行试验研究。
基于相位调制的1090ES扩容信号采用对PPM信息进行脉内调相的双重调制方式,通过对PPM信息和相位扩容信息分开解调进行信息提取,其中,由于ADS-B系统中本地频率振荡器输出频率的不稳定性及多普勒频移等原因引起的载波频率偏移,将严重影响扩容信息相干解调的性能。此外,对于单发多收的ADS-B突发通信系统,其突发传送模式以数据包为单位传送数据,某一数据包在解调前所得到的同步等相关信息往往不能被下一个数据包所利用,每一个数据包都需要重新估计各种同步等参数。因此,对于ADS-B突发通信信道,如何在短时间内实现载波同步具有重要的研究意义。
文中针对基于相位调制的ADS-B扩容系统,研究其载波同步问题,构建了1090ES相位编码信号的频偏估计模型,并在此基础上提出了一种基于遗传算法(Genetic Algorithm, GA)的频偏估计算法,详细叙述了该算法的特点及其实现步骤,并与其它基于数据辅助的频偏估计算法做了仿真分析比较。
11090ES相位编码信号中的载波同步问题
1.11090ES相位编码信号模型
对于1090ES相位编码信号,采用的载波同步方案为首先利用接收信号进行载波频偏估计,之后直接采用相位旋转进行频偏校正。
基于相位调制的1090ES扩容信号的数据链结构如图1所示。

图1 1090ES扩容信号的数据链结构
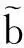
假设已正确提取PPM信息,并利用PPM信息完成了对1090ES扩容信号的码元同步,则采样后的接收信号可表示为:
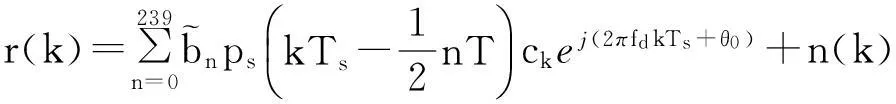
k=1,2,3,…,L
(1)

(2)
(3)
式中,n′(k)仍服从高斯分布。从一系列采样值{z(k),k=1,2,…,L}中,估计出频偏fd是频偏估计的根本问题。
1.2基于数据辅助的频偏估计算法
由图1可知,1090ES扩容数据链具有8 μs的应答报头,其中的四个前导脉冲不携带数据信息,可用来调制已知相位信息,作基于数据辅助的频偏估计。
基于数据辅助的频偏估计算法主要分为两大类,一类是基于采样值{z(k),k=1,2,…,L}相位的频偏估计器,Tretter提出的频偏估计算法通过展开采样值相位,再通过线性回归运算获取待估计频偏[4],该算法估计效果接近最大似然估计,但是相位展开增加了估计器的运算量,尤其是在信噪比较低时,相位展开运算较为复杂。在Tretter算法的基础上,Kay提出了一种基于差分相位频偏估计算法[5],避免了Tretter算法中存在的问题,其频偏估计范围较大,可达到采样频率的40%,但是Kay算法的信噪比门限较高,且估计精度不高。另一类基于数据辅助的频偏估计算法是通过计算采样值{z(k),k=1,2,…,L}的自相关函数获取待估计频偏,典型代表算法有Fitz算法[6-8]、L&R算法[9]及M&M算法[10]等,这类算法具有较高的估计精度,但是难以兼顾其频偏估计精度和频偏估计范围。
本文提出了一种不同于以上两类的频偏估计算法,该算法通过在频偏估计范围内进行高效启发式搜索,获得最优频偏估计值,频偏估计范围可以达到采样频率的50%,估计误差在低信噪比时接近修正的克拉美罗界(Modified Cramer-Rao Bound,MCRB)。本文提出的基于GA的频偏估计算法具有比Kay算法更低的信噪比门限,比Fitz算法及M&M算法更大的频偏估计范围,并且其频偏估计范围独立于频偏估计均方误差。
2基于遗传算法的频偏估计
2.1基于GA的频偏估计模型
观察式(3)所示的采样信号,待估计载波频偏和载波初始相位,可以从下面的最小二乘问题中得到:
(4)
满足上式的η就是我们要估计的载波频偏的变换值。
本文提出了一种基于GA的频偏估计算法,它利用GA在频偏及初始相位的可搜索范围内寻找最优值,求解式(4)所示的最小二乘问题,估计出的载波初始相位为:
(5)
载波频偏为:
(6)
本文只分析载波频偏估计问题。
2.2基于GA的频偏估计算法
遗传算法是模仿自然界生物进化机制发展起来的随机全局搜索和优化方法,它能在搜索过程中自动获取和积累有关搜索空间的知识,并自适应的控制搜索过程以求得最优解。遗传算法操作使用适者生存的原则,在潜在的解决方案中逐次产生一个近似最优解的方案,在遗传算法的每一代中根据个体在问题域中的适应度值和从自然遗传学中借鉴来的再造方法进行个体选择,产生一个新的近似解。这个过程导致种群中个体的进化,得到新个体比原来个体更能适应环境,就像自然界中的改造一样。
基于遗传算法的频偏估计算法步骤可以简述如下:

(7)
因此,归一化频偏搜索范围设置为-0.5~0.5。
(2)建立频偏估计算法的目标函数,如式(4)所示;
(3)确定表示可行解的个体编码方法。在该算法中,用8位二进制数表示染色体个体,因此,可行解的编码即是将十进制归一化频偏转换为8位二进制染色体;
(4)确定解码方法,即将8位二进制染色体转换为十进制归一化频偏;
(5)确定个体适应度的量化评价方法,即确定出由目标函数值到个体适应度的转换规则。在该算法中,目标函数是一个最优化问题,可将其确定为适应度函数;
(6)设计遗传算子:选择运算使用比例选择算子,交叉运算使用均匀交叉算子,变异运算使用基本位变异算子。
(7)确定遗传算法的运行参数:群体大小设置为80,终止进化代数设置为200,交叉概率设置为0.8,变异概率为0.1,最优保存概率设置为0.1。
2.3基于GA的频偏估计算法特点
遗传算法在频偏估计范围内进行高效启发式搜索,从由很多个体组成的一个初始群体开始最优解的搜索过程,而不是从一个单一的个体开始搜索,这是遗传算法所特有的一种隐含并行性,可通过大规模并行计算来提高计算速度,因此遗传算法的搜索效率较高。
遗传算法仅使用由目标函数值变换来的适应度函数值,就可以确定进一步的搜索方向和搜索范围,无需目标函数的导数值等其他一些辅助信息,算法简单易实现。
此外,遗传算法使用概率搜索技术,选择、交叉、变异等运算都是以一种概率的方式来进行的,因而遗传算法的搜索过程具有很好的灵活性。随着进化过程的进行,遗传算法新的群体会更多的产生新的优良个体,直至产生全局最优解。
基于遗传算法的频偏估计性能将在下一节作详细分析,并与其他基于数据辅助的频偏估计算法作对比,如Kay算法、Fitz算法及M&M算法,频偏估计表达式[11]如下所示。
Kay频偏估计算法的表达式如式(8)所示:
(8)


k=1,2,3,…,L-1
(9)
Fitz频偏估计算法的表达式如式(10)所示:
(10)


(11)
Fitz算法的频偏估计范围为:
(12)
M&M频偏估计算法的表达式如式(13)所示:
(13)


(14)
M&M算法的频偏估计范围为:
(15)
3基于遗传算法的频偏估计性能
本节将主要通过频偏估计范围,频偏估计均方误差及信噪比门限三个指标,来比较本文所提出的基于GA的频偏估计算法与Kay算法、Fitz算法及M&M算法之间的工作性能差别。
3.1频偏估计范围
取采样点个数L=8,取N=L/2,采样时间间隔Ts=0.5 μs,信噪比SNR=5 dB。
基于遗传算法、Kay算法、Fitz算法及M&M算法的频偏估计范围如图2所示。

图2 各种频偏估计算法的频偏估计范围
3.2频偏估计均方误差及信噪比门限
取采样点个数L=8,取N=L/2,采样时间间隔Ts=0.5 μs,归一化待估计频偏fdTs=0.01。
基于GA、Kay算法、Fitz算法及M&M算法的归一化频偏估计均方误差如图3所示,并以MCRB为基准,比较各算法的频偏估计性能,MCRB如式(16)所示[12]:
(16)

图3 归一化均方误差
由图3可知,基于GA的频偏估计算法的信噪比门限在0~3 dB之间,与Fitz算法及M&M算法相当,Kay算法的信噪比门限较高,在5~7 dB之间。
改变采样点个数L,其他参数保持不变,则各算法的频偏估计均方误差如图4所示。

(a)不同采样点时,基于GA频偏估计算法的归一化频偏估计均方误差
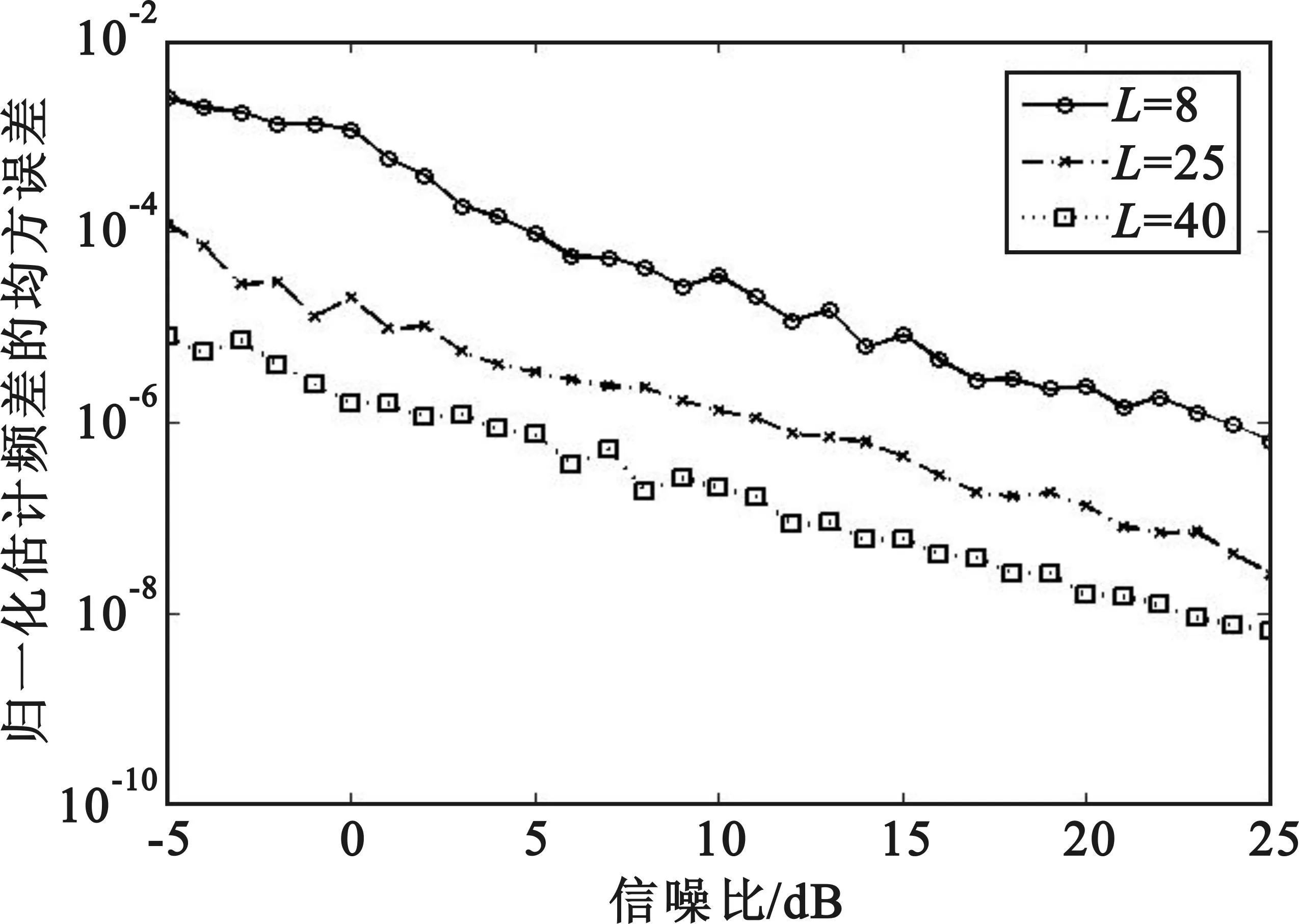
(b)不同采样点时,Fitz算法的归一化频偏估计均方误差

(c)不同采样点时,M&M算法的归一化频偏估计均方误差
由图4可知,当采样点数增加时,基于GA、Fitz算法及M&M算法的归一化频偏估计均方误差都会相应减小。不同的是,Fitz算法及M&M算法的精确度提高是以牺牲频偏估计范围为代价,而对于基于GA的频偏估计算法,改变采样点个数,并不会影响遗传算法的频偏搜索空间,也就是说它可以同时兼顾频偏估计精度和频偏估计范围。
4结语
本文研究了基于相位调制的1090ES扩容系统中的载波同步技术,提出了一种基于GA的频偏估计算法。仿真结果表明,该算法具有比Fitz算法及M&M算法更大的频偏估计范围,可以达到采样频率的50%;具有比Kay算法更低的信噪比门限,大约为3 dB左右;同时,增大频偏估计精度并不会以减小频偏估计范围为代价。本文提出的估计算法为提取1090ES相位编码信号中的扩容信息奠定了基础,而且它可以同时估计载波频偏和载波初始相位,载波初始相位的估计性能,将在以后作进一步分析。
参考文献:
[1]Thompson S D, Sinclair K A. Automatic Dependent Surveillance-Broadcast in the Gulf of Mexico[J].Lincoln Lab,2007, 1(17):55-69.
[2]Radio Technical Commission for Aeronautics (RTCA) Inc. DO-260B[S]. Washington, DC, 2008.
[3]Stayton G T, Peoria. Systems and Methods for Providing an Advanced ATC Data Link[P].United States, US 8,344,936 B2. 1,1,2013.
[4]Tretter S. Estimation the Frequency of Noisy Sinusoid by Linear Regression[J].IEEE Trans. on Information Theory, 1985, 31(6): 832-835.
[5]Kay S. A Fast and Accurate Single Frequency Estimator[J].IEEE Trans. Acoust. Speech Signal Process, 1989, 37(12): 1987-1990.
[6]Fitz M P. Planar Filtered Techniques for Burst Mode Carrier Synchronization[J].IEEE GLOBECOM, 1991, 12.
[7]Fitz M P. Further Results in the Fast Estimation of a Signal Frequency[J].IEEE Trans. Comm., 1994, 42(4): 862-864.
[8]Fitz M P, Lindsey W C. Decision-Directed Burst Mode Digital Carrier Synchronization Techniques[J].IEEE Trans. Comm, 1992, 40:1644-1653.
[9]Luise M, Reggiannini R. Carrier Frequency Recovery in All-Digital Modems for Burst-Mode Transmission[J]. IEEE Trans. Comm., 1995, 43: 1169-1187.
[10]Mengali U, Morelli M. Data-Aided Frequency Estimation for Burst Digital Transmation[J]. IEEE Trans. Comm., 1997, 45(1):23-25.
[11]龚岳洲,周新力,王文琰等.一种基于自相关函数的载波频偏估计方法[J].通信技术,2012,45(11):4-7.
GONG Yue-zhou, ZHOU Xin-li, WANG Wen-yan, et al. A Carrier Frequency Offset Estimation based on Autocorrelation Function[J].Communications Technology, 2012,45(11):4-7.
[12]Ho K C. Modified CRLB on the Modulation Parameters of a PSK Signal[J].IEEE, 1999: 40-44.

宋妍(1991—),女,硕士,主要研究方向为雷达信号处理、高速实时信号处理;
王洪(1974—),男,博士,副教授,主要研究方向为雷达信号处理、多点定位、数字接收机和高速实时信号处理等;
何东林(1976—),男,硕士,工程师,主要研究方向为信号与信息处理、多点定位、智能控制系统等;
黄忠涛(1978—),男,硕士,高级工程师,主要研究方向为雷达测试技术、嵌入式系统、视频仿真技术、场面监视系统等;
孙清清(1990—),男,硕士,主要研究方向为雷达信号处理、高速实时信号处理。
A Synchronization Algorithm of 1090ES Phase-Coded Signal
SONG Yan1, WANG Hong1, HE Dong-lin2, HUANG Zhong-tao2, SUN Qing-qing1
(1.University of Electronic Science and Technology of China, Chengdu Sichuan 611731,China;
2.The Second Research Inst. of Civil Aviation Administration of China, Chengdu Sichuan 610041,China)
Abstract:Carrier synchronization is the premise and basis for coherent demodulation of phase-coded signal. This paper discusses data-aided frequency offset estimation algorithm in 1090MHz Extended Squitter, 1090ES ( Extension System ).A novel frequency estimation model suitable for 1090ES phase-coded signal is constructed, and a frequency offset estimation algorithm based on genetic algorithm also proposed. The characteristics and implementation steps are described in detail, and the frequency offset performance is analyzed and compared with Kay algorithm, Fitz algorithm and M&M algorithm via MATLAB simulation.Experiment results show that the frequency offset estimation range of the proposed algorithm can reach 50% of the sample frequency, and the mean square error of frequency offset estimation is close to MCRB when SNR is lower 3dB. In addition, the proposed algorithm could give consideration to both estimation precision and estimation range.
Key words:1090ES; frequency offset estimation; data-aided; genetic algorithm
作者简介:
中图分类号:TN91
文献标志码:A
文章编号:1002-0802(2015)07-0762-05
基金项目:国家自然科学基金重点项目(No.61139003)
收稿日期:修回日期:2015-06-01Received date:2015-02-01;Revised date:2015-06-01
doi:10.3969/j.issn.1002-0802.2015.07.002
