球头铣刀倒棱刃磨削砂轮轨迹建模

计伟++刘献礼++李录彬++王广越++范梦超

摘要：针对带有倒棱切削刃的球头铣刀的磨制中砂轮轨迹生成问题，首先采用解析几何的方法通过坐标系变换，建立了铣刀顶刃切削刃和倒棱面模型，并通过确定倒棱面方程中长度和角度参数的关系进而得到倒棱面磨削轨迹；然后分析了砂轮与倒棱面的接触关系，选用了平行砂轮，在此基础上建立了磨削球头铣刀倒棱面的砂轮中心轨迹和砂轮轴矢量数学模型；最后通过Matlab软件对磨削倒棱面的磨削轨迹、砂轮中心轨迹和轴矢量进行仿真，并采用Saacke磨床磨制了刀具样件，结果表明所建立的数学模型的正确性.

关键词：倒棱切削刃；球头铣刀；磨削轨迹；砂轮中心；砂轮轴矢量

DOI：10.15938/j.jhust.2015.05.007

中图分类号：TG501

文献标志码：A

文章编号：1007-2683（2015）05-0034-05

0 前言

球头铣刀作为曲面加工刀具被广泛地应用于模具制造、汽车制造及航空航天等领域.汽车覆盖件模具常采用淬硬钢材料，硬度可达到HRC58-63，切削阻力大刀具磨损和破损严重.为了提高模具的性能，部分模具采用镶块式淬硬钢模件拼接后整体铣削加工而成，由于模具淬火表面和镶块硬度差一般超过HRC5-15，且型面加工特征多变，加工过程中引发载荷突变，因此加剧刀具的磨损破损.在加工淬硬钢硬度拼接模具时，普通球头铣刀易出现刀具崩刃和破损，影响模具加工效率.有学者提出采用带有倒棱的球头铣刀可以有效地提高球头铣刀的切削刃强度，目前，使用一般数控工具磨床的加T软件无法磨制带倒棱刃球头铣刀.因此，研究带倒棱刃球头铣刀的数学模型及磨削轨迹对实现其刀具的磨制非常重要，

球头铣刀磨制砂轮的轨迹和姿态的建模主要有两种方法：逆向设计和正向设计.采用逆向计算，两轴联动不能对刀具端刃的磨削过程进行很好的控制，从而不能充分满足刀具的强度要求和刀具排屑性能的要求.而正向计算采用标准砂轮，虽然砂轮轨迹计算复杂且磨床的配置要求较高，但是可以充分的考虑刀具几何形状以满足加工要求，因此本文采用正向计算的方法求解球头铣刀的磨削轨迹.

为了实现带倒棱刃球头铣刀的磨制，本文采用正向计算的方法求解带有倒棱结构球头铣刀磨制时砂轮的中心轨迹和轴矢量数学模型.

1 倒棱面及磨削轨迹建模

刀具建模的方法主要是基于微分几何和基于解析几何的，本文采用解析几何的方法建立刀具的几何模型.

整体硬质合金球头铣刀的切削刃是由半球面与螺旋面相交合成的，根据螺旋面的属性，其刃线种类可分为2种，等导程刃线和等螺旋角刃线.等导程刃线的加工性强，多应用于实际生产加工中，等螺旋角的刃线具有较好的切削性能，但其在刀具的顶点没有意义.下面分别建立等导程切削刃球头铣刀的切削刃模型、倒棱面模型和倒棱磨削轨迹模型，

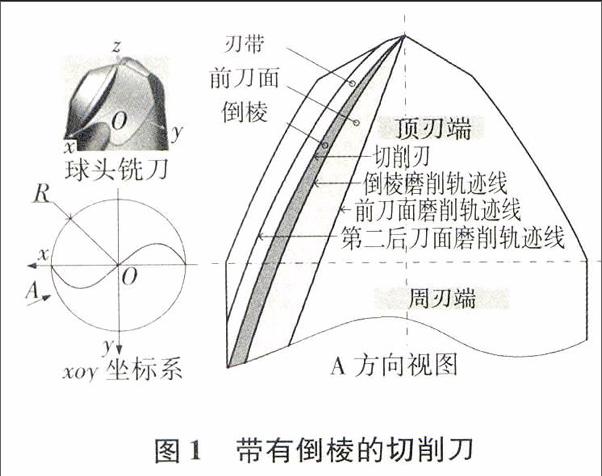
图1为建模坐标系，以刀具顶端球球心为原点，以刀具轴线有z轴，建立xyz坐标系，

采用半球面和正交螺旋面相交的方式作为切削刃线，其方程如式（1）所示，

其中，R为刀具直径， 螺旋角， 为角度参数，并且

倒棱面是复杂的三维曲面，在如图1所示的坐标系xyz下直接建模比较困难.因此，首先转换坐标系，如图2所示，包括坐标系xyz、xyz₁和xyz₂.其中，切削刃切线T如式（2）所示.

根据T与坐标系之间的关系，可以求出T与z轴的夹角θ和T与x轴在xoy平面的夹角ρ，分别如式（3）和式（4）所示.

根据图2中坐标系xyz、xyzi和xyz2之问的变换关系，可知xyz和xyz₁之间以及xyz₁和xyz₂的坐标系变换矩阵，分别见式（5）和（6）.通过这两个公式可以计算xyz与xyz₂之间的变换矩阵，见式（7）.

为了建立倒棱面模型，根据中的几何关系，可知 .因此，在xyz2中，倒棱面上的点Q的坐标为，

将式（8）代人式（7）即可得到倒棱面在xyz坐标系下的方程.

倒棱面与前刀面的交线即为倒棱面磨削轨迹.倒棱面所在曲面已求得，可通过确定式中长度参数2与角度参数φ的关系，来计算轨迹线.现已知l和φ的的范围，因此这两个参数可以用平面直角坐标系表示，如图3所示，从点 到点 的连线即可表示l和φ的关系，图中，不同的区域有不同刀具倒棱面的几何特征，在L₂区域中，倒棱面的整体面积大，但在近刀具顶点区域倒棱宽度的变化大；相反地，在厶区域中，倒棱面面积小，但在近刀具顶点区域倒棱宽度变化小；而在L₁区域中，倒棱面面积和倒棱宽度变化适中.

本文以图3中L₃区域中的一条抛物线为例说明建模过程，此抛物线顶点为 ，并且过点 ，开口向上，故可得其方程，

通过将式（9）代入倒棱面方程即可得到倒棱面磨削轨迹.

2 砂轮中心轨迹及轴矢量建模

在刀具模型和磨削轨迹的基础上，为了磨制球头铣刀倒棱面，确定砂轮的轨迹和空间姿态.

2.1 砂轮刀位点轨迹建模

砂轮刀位点轨迹是指砂轮定位基准点在磨削加工时的轨迹线.砂轮的刀位点轨迹线与刃磨轨迹线、砂轮的尺寸以及砂轮与磨削面的位置关系有关，本文采用平行砂轮的外圆周磨削倒棱面，图4为球头铣刀顶刃刃磨示意图，其中砂轮刀位点为M.则砂轮的刀位点轨迹M在xyz₂坐标系下的坐标如式（10）所示，

将点M在xyz₂下的坐标代人式（7），即可得到M点在xyz坐标系下的坐标.

2.2 砂轮轴矢量建模

砂轮轴矢量是砂轮的轴线的方向向量T_w，如图4所示.砂轮轴矢量与刃磨轨迹、砂轮尺寸及砂轮和倒棱面接触关系有关，根据图4中顶刃磨削过程中

砂轮面与倒棱面的关系，则有可得到砂轮轴矢量T_w在xyz₂下的坐标，见式（11），将其代入式（7）即可得到T_w在xyz下的表达式.

3 砂轮轨迹和轴矢量仿真与刀具磨制

为了验证模型球头铣刀倒棱面的磨削轨迹，砂轮中心轨迹及砂轮轴矢量的正确性，本文采用Matlab软件对以上模型进行仿真.

设定刀具和砂轮的参数，刀具的倒棱参数为： 砂轮参数：砂轮半径R_w=10mm（为了清晰的观察倒棱面磨削仿真图，仿真中砂轮直径的设置比实际小）.

图5为刀具顶刃刃磨削轨迹、砂轮中心点轨迹及砂轮轴矢量仿真图.砂轮中心轨迹及轴矢量可以确定砂轮的运动和空间姿态，并且通过与刀具的相对运动进而形成刀具的倒棱面.然后根据球头铣刀倒棱刃磨削的砂轮中心轨迹和砂轮轴矢量，使用Saccke UWIF CNC刀具磨削加工中心，经过刀具工件坐标系和机床坐标系的变换，将砂轮中心轨迹的X、y和Z坐标及A和B旋转轴的数据输入机床，即磨制出带有倒棱刃的球头铣刀，如图6所示.

结合砂轮轨迹与轴矢量仿真结果，证明本文所建立的刀具倒棱面磨削中所涉及到的数学模型的准确性.通过刀具样件的磨制结果，证明本文建立的砂轮中心轨迹模型可用于球头铣刀倒棱刃的磨制.

4 结论

本文通过对带有倒棱刃球头铣刀磨制过程中砂轮姿态的分析，得到如下结论：

1）建立了带倒棱刃球头铣刀的切削刃、倒棱面和磨削轨迹模型，并且通过正向计算建立了磨削球头铣刀倒棱面时砂轮中心轨迹及砂轮轴矢量的数学模型，为带有倒棱面的球头铣刀的磨制提供r基础模型；

2）通过对倒棱面磨制的磨削轨迹、砂轮中心轨迹和轴矢量模型进行仿真，验证了所建立的数学模型的正确性；

3）通过带有倒棱刃的球头刀的磨制，证明本文所建立的砂轮轨迹和轴矢量模型可用于加工球头铣刀的倒棱刃.