双馈风力发电系统转子侧功率控制策略研究

付敏++盖凯凯++林悦铭

摘要：在电网电压稳定和降落时，要求双馈风力发电系统能够根据系统的需求及时的调整功率的输出.分析了双馈风力发电机的数学模型，在电网电压稳定时采用传统基于电网电压定向的矢量控制，在电压降落时采用计及定子电压波动的改进控制策略.利用Matlab/Simulink搭建系统仿真模型，仿真结果表明：在电网电压稳定和电网电压降落时有效实现有功功率和无功功率的解耦.电网电压降落时，双馈风力发电机能够实现无功调压.采用PI控制器，系统响应快、超调小，验证了控制策略的准确定性，

关键词：双馈风力发电系统；电网电压降落；功率控制；无功调压

DOI：10.15938/j.jhust.2015.05.004

中图分类号：TM273

文献标志码：A

文章编号：1007-2683（2015）05-0020-05

0 引言

双馈风力发电系统的功率控制技术是研究风力发电系统的关键技术之一.双馈风力发电机（DFIG）转子侧主要控制发电机向电网输送有功功率和无功功率.有功功率通过最大风能追踪控制策略实现有功功率的输出；无功功率根据电网的需求来调节功率因数.主要有矢量控制策略和直接功率控制技术和自适应控制等技术.

在电网稳定运行时，传统的控制策略都忽略了定子电压的动态变化量和磁链的动态变化量，使控制模型得以简化，便于模型的搭建.但从系统的运行来看，由于电网负荷的增减等因素都造成电网电压的波动，而电网不可能一直保持稳定运行状态，因此研究在电网电压波动时，使双馈风力发电机的能够良好的适应电网的波动，对提高双馈风力发电系统的鲁棒性具有重要意义.

本文考虑到电网电压降落和风速变化两个因素对双馈发电机及其控制策略的影响，在理想电网基础上，提出改进基于电网电压定向的矢量控制策略，通过Matlab/Simulink搭建系统仿真模型，在理想电网和电网电压降落情况下，系统实现了有功功率与无功功率独立控制以及无功调压.

1 双馈风力发电系统数学模型

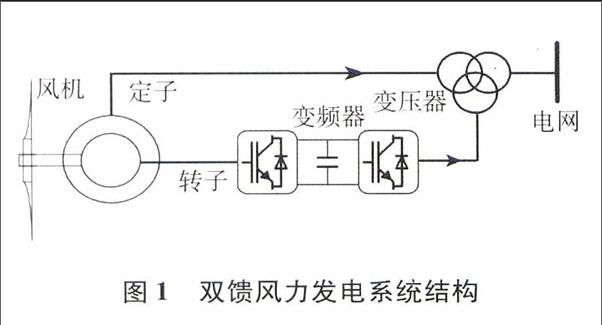
双馈发电机是一个高阶、非线性、强耦合的多变量系统.其系统结构如图1所示.

1.1 双馈风力发电机的数学模型

以同步旋转dq为坐标系，定子、转子均采用电动机惯例，双馈发电机的数学模型如下：

定、转子电压方程可表示为（略写零序分量）：式中：u_ds、u_qs、u_dr、u_qr分别为定子、转子电压的d、q轴分量；i_ds、i_qs、i_dr、i_qr分别为定子、转子电流的d、q轴分量；ψ_ds、ψ_qs、ψ_dr、ψ_qr分别为定子、转子磁链的d、q轴分量；r_s、r_r分别为定、转子的电阻；L_s、L_r、L_m分别为定、转子的白感和互感；ω₁、ω_r分别为同步转速和实际转速.

1.2 改进转子侧控制侧略

在双馈风力发电机模型基础之上，推导出定子电流、转子磁链方程如下：

由式（6）或（7）中看出，传统的控制策略中，只考虑到了电压的稳态分量和稳态电压补偿项，忽略了电压的动态分量.在电网稳定运行时，忽略动态分量对于系统没有影响，但当电网电压发生波动时，该控制策略就具有一定的局限性，因此改进的控制策略中，考虑到定子电压的波动对于系统的影响，将电压的动态分量加入到定子电压中，使系统更好的适应电网电压的波动，提高控制模型的准确性，

采用基于电网电压定向的改进矢量控制策略，其坐标表示如图2所示.u_ds=u_s，u_qs=0，ψ_ds=O，u_s为电网电压的幅值，忽略了定子电阻，则q轴的磁链可近似为： .将其代人到式（6）中，转子电压方程为：

定子输出的有功无功功率为

由上式可以看出，分别调节转子d轴电流i_dr和q轴电流i_qr可实现对有功功率和无功功率的解耦控制，当电网电压降落时，控制系统保持有功功率基本不变，使其仍很好的跟随最大风能追踪，而通过增加无功功率，可以补偿电网电压的降落，从而实现了无功参与调节电网电压，

传统的基于定子电压定向的矢量控制策略，忽略了电网电压的波动对系统的影响，使控制系统得以简化，但其只能运行在理想电网条件下，具有一定的局限性，改进的控制策略考虑到定子电压、电流、磁链的动态变化，重新推导转子电压方程，将电网电压的动态变化量加入到转子侧的电压中.与传统的控制策略相比较，在电网电压波动时，转子侧电压能及时跟随电网电压的变化而实时调整，提高了控制的准确性和系统的鲁棒性并实现电网降落时无功调压.

1.3 改进基于电网电压定向的矢量控制系统

网侧控制策略参考文献，本文不再赘述.发电机励磁系统采用双闭环的PI控制结构.外环为功率控制环，内环为电流控制环.相比于电流外环和转速内环闭环控制，通过给定功率参考值，将定子输出功率与转子电流和电压建立直接关系，提高了系统控制的准确性.本文采用基于功率给定的MPPT控制策略，将风机输出功率作为系统的参考功率，无功功率参考值则根据系统的需求给出，采用PI控制器，在传统的控制策略基础之上增加了动态补偿项，经坐标变换，作为SVPWM的控制信号.改进的控制策略系统与传统控制策略系统相比较，增加了电网电压的动态分量，增加模型的利用范围，提高了整个系统的鲁棒性.其控制结构如图3所示.

2 P-Q解耦控制方案仿真分析

利用Madab/Simulink为平台，搭建双馈风力发电系统模型.设置系统仿真参数如表1所示.

2.1 电网电压稳定下的仿真

仿真从稳态开始.设定风速变化范围为：风速从

3 s开始阶跃变化，由5m/s变为6m/s；在5s时第二次发生阶跃变化，由6m/s变为7m/s，在7s时风速7m/s变为6.5m/s，并保持恒定.其仿真波形如图4所示.

图4（a）中，随着风速的增加，有功功率增加，而风速减小，则有功功率减小，表明DFIG很好的跟随了风机的输出功率，验证了基于功率给定的最大风能追踪控制策略的准确性.同时，在3s、5s、7s时，有功功率变化，无功功功率保持不变，在4s时无功功率参考值由0变为IOkvar，6s时变为8kvar，有功功率保持不变，验证了改进的基于电网电压定向的控制策略能够有效的实现有功、无功功率解耦.同时，在风速变化时，有功功率响应速度快，超调小，表明PI控制器能够快速准确的满足系统的响应.图4（b）中，电流有功分量i_dr、无功分量i_qr也实现解耦，因此分别调节i_dr、i_qr可以实现有功、无功功率的解耦.图4（c）中，采用给定功率的MPPT控制策略，将风机输出有功功率作为DFIG的功率参考值.图为参考功率与实际功率的误差值，其误差值几乎为0，可以看出，实际有功功率能很好的跟随参考值的变化，表明系统控制策略的准确性.

2.2 电网电压降落时的仿真

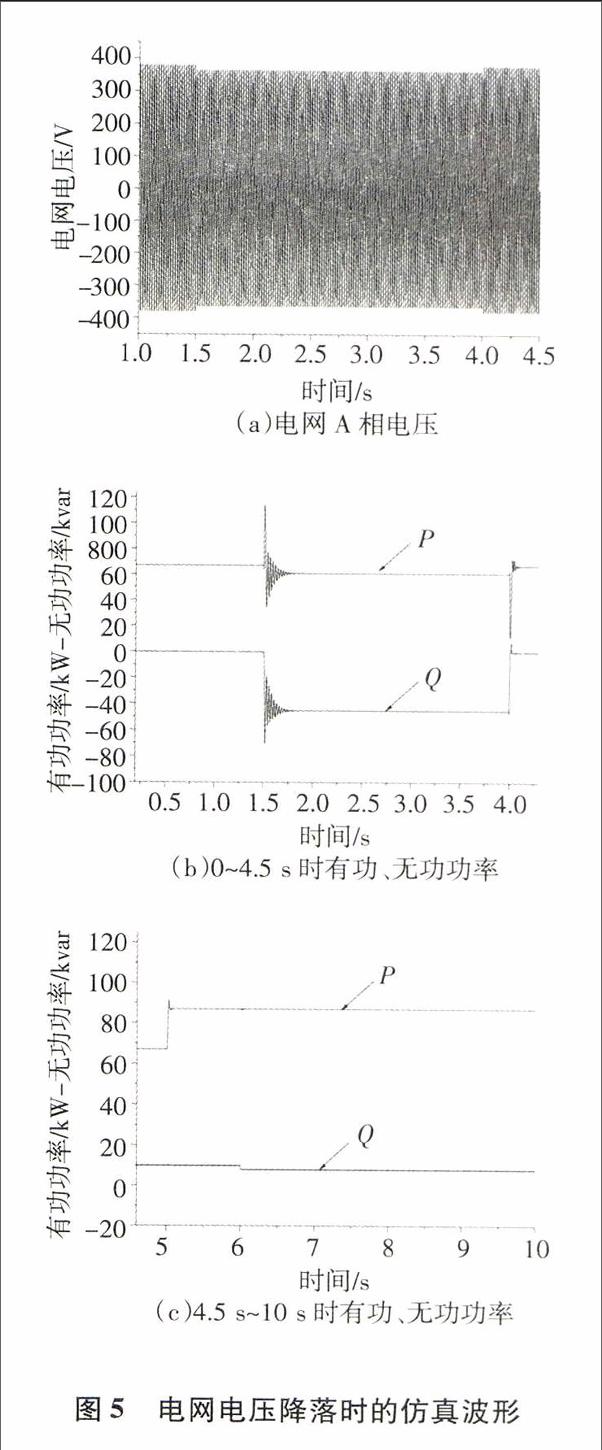
在电网频率恒定的条件下，电网在1.5s时，电网电压骤降为365V，在4s时恢复到初始值380V.风速在Ss时由5m/s变为6m/s.采用改进控制策略，其仿真结果如图5所示，

在电网电压波动时，图5（a）中，电网电压在1.5～4s时降落15V，图5（b）中，有功功率随着电压降低而降低，但变化范围不大，电机仍能正常发出有功功率.无功功率的给定值设为0var，在1.5s时电压骤降，1.5～4s内无功功率负向增大，由于双馈电机采用电动机惯例，Q

3 结语

双馈风力发电系统的有功功率和无功功率的解耦是其控制的关键技术之一.本文给出了DFIG数学模型，重新推导了转子侧电压公式，提出了改进的基于电网电压定向的控制策略.与传统控制策略相比，增加了电网电压的动态分量，克服了传统控制策略只运行在理想电网条件下的局限性，增加了系统控制的准确性和鲁棒性.实验结果表明，在两种电网条件下，都可以很好的实现有功功率和无功功率的解耦控制.在电网电压降落时，DFIG能够根据系统的需求，增加无功功率的输出，从而实现了DFIG的无功功率的调整，进而实现电压的调整.整个系统响应速度快，超调小，具有一定的工程应用意义，