旋流器分离的平衡轨道理论研究

罗建国

(阳泉煤业(集团)有限责任公司 新景矿洗煤厂，山西 阳泉 045000)

旋流器分离的理论学说众多，比较著名的有湍流两相流理论、平衡轨道理论、停留时间理论、底流拥挤理论和随机轨道理论等[1-2]，其中平衡轨道理论是目前发展最成熟、应用最广泛的理论。该理论最早由Driessen于1951年提出，后经Criner、Kelsall、庞学诗、姚书典等国内外众多学者的继承和发展[1-4]，根据分离面位置和形状选择的不同，又衍生出许多重要分支，如最大切线速度轨迹面、零轴速包络面及溢流管等径圆柱面理论等。平衡轨道理论的核心思想包括[3-4]：①不同粒径(或密度)的粒子最终将处于各自的平衡轨道面上，该面上的粒子径向速度和加速度均为零，其仅作旋转和轴向运动；在径向上，由中心至器壁，随着半径的逐渐增大，粒子的粒径(或密度)也逐渐增大，当粒子粒径大于平衡面上旋流器器壁处的粒径时，受器壁的限制，其只能紧贴器壁。②平衡轨道面上位于旋流器分离基准面以外的粒子，均随外旋流从底流口排出，反之则随内旋流从溢流口排出，刚好在分离面上的粒子则等概率的随底流或溢流排出，该处的粒径即为分离粒度。

与其它理论学说相比，平衡轨道理论具有物理意义清晰、简单明了、推导过程易于实现等优点，且由此推导出的分离粒度(也叫切割粒径)计算数学模型形式简单、无经验常数、适应性强、计算方便、预测精度高，因此，其在实践中获得了广泛应用。但该理论也存在部分不足——理论描述过于理想化，将粒子看成完全按精准化分离，没有考虑停留时间和湍流等因素的影响，有待进一步完善和发展。

1 运动方程的建立

对于旋流器内的粒子运动方程，比较著名的是BBO方程[5]，它同时考虑了离心力、向心浮力、流体曳力、惯性力、视质量力、Basset力的作用，但其比较复杂，在实际应用中受到很大限制。平衡轨道理论的粒子运动方程在BBO方程的基础进行了简化，忽略了部分次要力的作用，只保留了前三个主要作用力。假定切向的粒子与流体运动速度相等，并定义由旋流器轴心指向器壁的方向为正方向，则其运动方程为[6-10]:

(1)

(2)

(3)

(4)

式中：d为粒子的粒径，m；ρm、ρ分别为粒子和流体的密度，kg/m3；vt、vr、vmr分别为流体的切向和径向速度、粒子的径向速度，m/s；r为粒子所处的位置半径，m；t为粒子在旋流器内的运动时间，s；FD为流体曳力，N；CD为曳力系数；A为粒子在流动垂直方向上的投影面积，m2；Re为雷诺数；μ为流体的动力粘度，Pa·s。

对于球形粒子，则有

A=πd2/4，

(5)

当Re≤0.1时，流体曳力为Stokes阻力，将式(3)-(5)代入式(2)，可得

FD=3πμd(vmr-vr)。

(6)

一般认为，对于粒径≤1 mm的粒子，其与流体间的相对运动可以近似看成层流状态，将式(6)代入式(1)，整理后可得

(7)

其中vt、vr可以通过计算机采用CFD软件求解流体连续性方程和N-S方程得到，但为计算方便，分别以近似经验式(8)和(9)[4，9]代替，

(8)

(9)

式中：ri、R、ru分别为旋流器的入料口和柱段、底流口半径，m；vi为旋流器入料口处矿浆流速，m/s；H、h分别为旋流器整体和溢流管长度，m。

在实际操作过程中，不能将式(1)中粒子的径向速度vmr与其相对于流体的径向速度(vmr-vr)混淆；上述粒子运动方程的建立忽略了粒子间的相互作用，因此，比较适用于低浓度矿浆的场合，但也有学者认为即使浓度高达28%也能满足[3]。

2 运动方程的求解

2.1 传统解法

多数专家学者[6-9，11-16]在对式(7)求解时直接将该式左边第三、第四项当作常量，按一阶非线性常微分方程求解，最终得出的特征解[6-7,9，15](初始条件中t=0、vmr=0)为：

(10)

当t→∞时，其存在最大值，则有

(11)

从式(10)可以看出，尽管在理论上t→∞时vmr才能取得最大值，但实际要达到此值的99%所需的时间仅为毫秒数量级。例如，对于μ=0.001 Pa·s、d=1×10-4m、ρm=2 000 kg/m3的入料，将相关数据代入式(10)可计算出，该粒子只需约5 ms即可达到最大值的99%；即使d=5×10-4m，所需时间也不超过0.13 s。因此，在忽略这段短暂的加速时间后，可以认为在初始阶段就有粒子满足最大沉降速度(即沉降末速)，即任何时间式 (11)都成立。

曹仲文、袁惠新等人[17]通过引入式vmr=dr/dt对式(11)进行积分求解，得出了r与t的关系式；其他研究[18]还通过引入式dvmr/dt=dvmr/dr·vmr，直接对式(7)进行微分变换再求解，但均没有求解出结果。梁政、任连城等人在得出(11)式后认为[9,15]：粒子在进入旋流器的瞬间即受力平衡而达到沉降末速，在整个沉降过程中径向合力几乎处处为零，不存在所谓的径向合力为零的轨迹面，但存在径向速度为零的轨迹面。

2.2 作者解法

将式(7)左边第三、第四项看作常量的传统解法处理不当，这是离心力场沉降有别于重力场沉降的特殊之处。如果梁政、任连城等人的上述结论成立，则这些粒子都将以沉降末速恒速运动，直至器壁(或中心)，不可能到达各自的平衡轨道面，也就无法有效分离，这与事实严重不符；从(11)式也可以看出，vmr所代表的沉降末速是随r变化的变量，这说明这些粒子并不是一直处于受力平衡状态。

实际上式(7)是以“粒子”作为参照系进行受力分析得出的，而粒子的径向速度vmr=dr/dt，即r是与t相关的变量。也就是说，式(7)中实质上隐含了一个vmr=dr/dt的方程，其应该是由这两者组成的联立方程组，其等效于如下方程,

(12)

将式(8)、式(9)代入式(12)，整理后可得

(13)

不难看出，式(13)是一个复杂的二阶非线性常微分方程，很难甚至不能求得精确解，但可以采用Matlab软件通过计算机编程求得近似解。所编程序如下：

function solve_odes

clear all;clc

format long

tspan=0∶0.01∶4;%(时间范围和步长，可以根据需要调整)

r0=[0.037 50];%(粒子初始位置，可以根据需要变换)

[t r]=ode15s(@myodes,tspan,r0);[t r(∶,1) r(∶,2)]

figure(1)

plot(t,r(∶,1),'r-',t,r(∶,2),'b-'),axis([min(tspan)-0.1 max(tspan)+0.1 min(min(r))-0.01 max(max(r))+0.01]),legend('r','drdt')

function dudt=myodes(t,u)

a=***;b=***;c=***;k=***;%(此处a、b、c、d必须根据式(13)代入具体数值)

dudt(1)=u(2);

dudt(2)=-a*u(2)+b*(u(1))^(-2.28)-a*c*(u(1)+k)^(-1);

dudt=dudt';

2.3 分离粒度模型的推导

尽管式(12)很难甚至不能求得精确解，但这并不妨碍人们对平衡轨道理论的应用。事实上，只需使该方程中的dr/dt=0且d2r/dt2=0(或式(7)中的dvmr/dt=0和vmr=0)[19]，即可回避直接求解微分方程的难题，进而得出

(14)

式(14)即为平衡轨道理论中的粒子径向分布通用数学模型，也是平衡轨道理论核心思想的理论来源；要使粒子按粒径大小精确分级，各粒子的密度必须接近。由于该式的推导过程不需要直接对微分方程求解，也因为式(11)与式(7)在dvmr/dt=0的条件下所得表达式吻合，导致许多学者在对式(7)方程求解错误的情况下仍得出正确的式(14)，从而没有影响到平衡轨道理论在实践中的正常应用。

对于式(14)，如果以分离基准面半径rc代替r，则d就变成了分离粒度d50。但由于不同的学者采用的vt和vr表达式及选择的分离面形状和位置等不同，有的还以不同的压力降(ΔP)计算式代替vi，导致最终推导出的d50计算模型存在很大差异。如将式(8)、式(9)代入式(14)，则可得

(15)

式中:rc为分离基准面位置半径，m。

从旋流器轴心至器壁的整个区域，流体的vt和vr都分别由多段函数组成，例如vt是由准自由涡和准强制涡共同组成的，两者的分界线在最大切线速度位置半径rm处；平衡轨道理论所采用的vt和vr表达式为处于准自由涡区域的函数，也就是说，用来描述粒子粒径沿径向分布规律的数学模型(即式(14)和式(15))只适用于rm≤r≤R的区域，而不是0≤r≤R的整个区域。

3 科学性论证

反对平衡轨道理论的学者认为，粒子在旋流器内没有足够的停留时间，故其不可能全部到达各自的平衡轨道位置[1]。为此，必须证明对于所有粒子，在理论上都能满足平衡状态的条件，即经过一段时间后，粒子的径向速度和加速度同时为零，且不再发生变化；在有效的停留时间内，绝大多数粒子都可以达到或近似达到平衡状态。

将计算出的a、b、c、d数值代入编写的Matlab程序，以求出粒子的运行轨迹。假设以溢流管等径圆柱面作为旋流器的分离基准面，旋流器的结构、入料性质、操作参数分别为：μ=0.001 Pa·s、ρm=2 000 kg/m3、ρ=1 000 kg/m3、R=0.037 5 m、ri=0.2R、r0=0.35R、L=2R、ru=0.2R、θ=20°、H≈6.5R、h=1.6R、vi=2.5 m/s、d=4×10-5m。将上述数值代入式(13)，可得到a=5 625、b=0.025 6、c=0.000 765、k=0.007 5，然后在Matlab软件环境下进行计算机模拟，并设定d2r/dt2≈Δ(dr/dt)/Δt，即可得出粒径0.04 mm的粒子的运动时间与运动路径、径向速度与径向加速度的对应关系(图1)。同理，可以分别取d=0.02 mm和d=0.01 mm(仅需将程序中a的值分别改为22 500和90 000)，进而得到粒径为0.02 、0.01 mm的粒子的径向运动轨迹(图1)。

对于粒子在旋流器内的平均停留时间，可以近似按式(16)通过计算得出。将上文假设的相关数据代入式(16)，计算出的粒子平均停留时间为1.40 s。

(16)

式中：t′为粒子在旋流器内的平均停留时间，s；L为旋流器的柱段长度，m；r0为旋流器的溢流口半径，m。

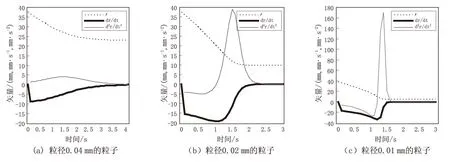
图1 不同粒子的径向运动轨迹

由图1可知：

(1)对于任意粒子，其径向位移始终向某一点(面)逼近，直至达到平衡状态；该点(面)即为对应粒径粒子的平衡轨道面，该位置处的粒子径向速度和加速度同时为零，且不再变化。

(2)粒子的径向速度方向和位移方向相同，都是始终指向平衡轨道面；其径向速度先从零迅速增大到某一值，再在该值附近平缓变化，然后快速下降，在即将接近平衡面时趋于平缓，最后为零且不再变化。

(3)粒子的径向加速度方向先与径向速度方向相同，但初始值非常大，随后瞬间降至与径向速度值同一数量级水平，接着其趋于零；在方向改变后继续增加，增大到某一值后逐渐减小，最后与径向速度同时趋于零且不再变化；在整个运动过程中，粒子两次通过零点。

(4)粒径为0.04、0.02、0.01 mm的粒子的平衡轨道面分别位于r=22.90、9.70、4.50 mm处，且从器壁到达各自的平衡轨道面所需的时间分别为4.10、2.60、1.80 s。粒径为0.02、0.01的粒子的平衡轨道面位于溢流管等径分离面(r=13.10 mm)以内，两者最终进入内旋流并从溢流口排出，其分离作用在溢流管壁处已完成，对应的时间分别为1.40、1.10 s，与平均停留时间接近，可以认为满足平衡轨道理论要求。粒径为0.04 mm的粒子，其达到平衡轨道面所需的时间明显大于平均停留时间，故不能满足平衡轨道理论要求；但该粒子到达距其平衡面0.1R(即3.75 mm)位置(即r=26.65 mm)所需时间为1.5 s，其与平均停留时间较接近，可以认为该粒子处于“准平衡”状态，即近似满足平衡轨道理论。

采用部分具有代表性的a、b、c、k值和初始位置(取器壁、中部和靠近溢流管处)进行进一步研究，所得结论与上述结论基本一致。结合上文假设的旋流器结构、操作参数和物料性质，还可计算出d50=0.026 mm，平衡面位置r=13.10 mm，达到平衡状态所需的时间为2.90 s，到达距其平衡面0.1R位置(r=16.85 mm)所需时间为1.50 s，其接近于平均停留时间，也可以认为这些粒子近似满足平衡轨道理论。由于这些粒子的初始位置选择的都是器壁，其达到平衡状态的时间相对较长；如果这些粒子处于其它位置，其达到平衡状态所需的时间更少，因此，可以认为绝大多数粒子在旋流器有效停留时间内都能够达到或近似达到平衡状态。

4 结论

通过对由离心力、向心浮力、流体曳力三个主要作用力建立的旋流器内部分散相粒子运动方程的分析，认为其并非简单的一阶常微分方程，而是一个复杂的二阶非线性常微分方程，很难甚至求解不出精确解，但可以利用Matlab软件编程通过计算机求出近似解。通过计算机的数值模拟求解，进一步加深和完善了对平衡轨道理论的认识，其核心思想可以概况为以下四点：

(1)平衡轨道理论的“平衡”是指粒子的径向受力和径向位置同时处于动态平衡，即粒子的径向速度和加速度同时趋于零，且不再发生变化，其只做旋转和轴向运动；该“平衡”不是完全物理意义的精准化平衡，而是“准平衡”，即不能保证所有粒子都处于平衡状态，但绝大多数粒子在最终分离前都能运动至以各自平衡面为中心，间距为±0.1R的狭窄环形区域面内。

(2)沿着旋流器半径由中心向器壁，粒子的粒径(密度)逐渐增大，不同粒径(密度)的粒子将处于各自的环形区域平衡面内；当粒径大于平衡轨道处于旋流器器壁的粒子粒径时，受器壁的限制，其只能紧贴器壁。

(3)每个粒子始终都有向自己的平衡轨道面运动的趋势，理论上其都能达到平衡状态，但受粒子在旋流器内停留时间的限制，并不是所有粒子最终都能达到平衡状态；即便对于同一粒径的粒子，由于其初始径向位置不同，到达平衡位置所需的时间也不同，即其运动具有一定的随机性。

(4)分离基准面应该是一个狭窄的环形区域面，最终位于该面以外的粒子都将随外旋流从底流口排出，反之则随内旋流从溢流口排出，刚好处于该面上的粒子则等概率的随底流或溢流排出，该处的粒径即为分离粒度。

平衡轨道理论的现实意义不仅仅在于其对粒子运动行为的合理解释和分离粒度的精确预测，更重要的是其为旋流器结构和操作参数的优化设计等提供了理论指导：该理论所提出的被选粒子按粒径(密度)大小沿旋流器径向有序分层排布的思想，可以确保旋流器在理论上获得最高的床层松散度和最低的错配物，最终实现最高分离效率和分离精度，这是其它理论学说无法比拟的。

[1] 王升贵，陈文梅，褚良银，等.水力旋流器分离理论的研究与发展趋势[J].流体机械，2005，33(7):36-40.

[2] 王志斌.水力旋流器分离过程非线性随机特性研究[D].成都：四川大学，2006：1-4.

[3] 赵庆国，张明贤.水力旋流器分离技术[M].北京：化学工业出版社，2003：115-119，9-11，170.

[4] 庞学诗.水力旋流器技术与应用[M]. 北京:中国石化出版社，2010:101-133，50-54.

[5] 徐继润，罗 茜.水力旋流器内固液两相间的相对运动(I)——颗粒运动方程及其求解[J].中国有色金属学报，1998，8(3)：487-490.

[6] 徐继润，罗 茜.水力旋流器内固体颗粒的沉降[J].化工矿山技术，1997，26(2)：20-23.

[7] 徐继润，罗 茜.水力旋流器流场理论[M].北京：科学出版社，1998：22-24，179-222.

[8] 赵立新，蒋明虎，李 枫，等.旋流器分散相液滴受力分析——液液水力旋流器速度场研究之五[J].石油机械，1999，27(5)：24-27.

[9] 梁 政，王进全，任连城，等.固液分离水力旋流器流场理论研究[M]. 北京：石油工业出版社，2011：69-78，94-109.

[10] SOUZA F J, SALVO R V, MARTINS D A M. Large eddy simulation of the gas-particle flow in cyclone separators[J]. Separation and Purification Technology, 2012,94(4): 61-70.

[11] 张 健,周力行.气固两相流中颗粒轨道运动方程的一组分析解[J].燃烧科学与技术，2000，6(3):226-229.

[12] 霍夫曼A C，斯坦因L E.旋风分离器原理、设计和工程应用[M].北京:化学工业出版社，2004:16-19.

[13] 吴柏志，赵立新，蒋明虎，等.水力旋流器内颗粒受力与运动分析[J].东北石油大学学报，2005，29(6):64-66.

[14] 李正兴，袁惠新,曹仲文.旋流式超重力场中液滴动力分析[J].化工装备技术，2005，26(4)：14-17.

[15] 梁 政，任连城，吴世辉.水力旋流器颗粒沉降速度与分离粒度研究[J].西南石油大学学报 ，2007，29(3)：173-176.

[16] 罗金耀，刘新阳，高传昌.滴灌用水力旋流器的颗粒分离粒度[J].武汉大学学报:工学版，2009，42(3)：305-307.

[17] 曹仲文，袁惠新.旋流场中分散相颗粒径向受力及径向速度方程[J].江南大学学报:自然科学版，2004，3(5)：498-501.

[18] 曹仲文，袁惠新.旋流场中分散相颗粒运动特性分析[J].矿山机械，2006，54(10)：80-82.

[19] ZHANG R, BASU P.A simple model for prediction of solid collection efficiency of a gas-solid separator[J]. Powder Technology, 2004,147 (9) 86-93.