基于H∞控制方法的机器人遥操作系统同步控制
2016-01-19张文安
张文安,程 琪
(浙江工业大学 信息工程学院,浙江 杭州 310023)
基于H∞控制方法的机器人遥操作系统同步控制
张文安,程琪
(浙江工业大学 信息工程学院,浙江 杭州 310023)
摘要:针对具有时变时延的机器人遥操作系统,提出了一种基于H∞控制的同步控制方法.通过反馈线性化将机器人遥操作控制系统描述为一类不确定线性时滞系统,其中的不确定性用于描述时变时延引起的系统动态.进而,采用积分不等式和Lyapunov-Krasovskii函数方法,给出了系统时滞依赖渐近稳定并具有给定H∞性能指标的一个充分条件,并基于线性矩阵不等式设计了H∞控制器.最后,通过仿真算例验证了所提出的H∞控制方法的有效性.
关键词:时变时延;遥操作;时滞系统;H∞控制;同步控制
AnH∞control approach to synchronization control of robot teleoperation
systems with time-varying delays
ZHANG Wenan, CHENG Qi
(College of Information Engineering, Zhejiang University of Technology, Hangzhou 310023, China)
Abstract:An H∞control approach to synchronization control of robot teleoperation systems with time-varying delays is presented in this paper. The robot teleoperation system is converted as an uncertain linear time-delay system model by using feedback linearization method, where the uncertainty is used to model the dynamics induced by the time-varying delay. A sufficient condition of the H∞performance for the teleoperation system is presented by applying the integral inequality and the Lyapunov-Krasovskii function method. Furthermore,the design method of H∞controller is given out by using linear matrix inequality method. Finally, simulations are presented to show the effectiveness of the proposed method.
Key words:time-varying delay; teleoperation; delay system; H∞control; synchronization control
遥操作系统既可以让机器人代替人类在危险恶劣环境下进行作业,又可以把人类的专业技能和聪明才智作用到正在远端执行任务的从机器人作业当中去.主从机械臂动力学模型是非线性且存在模型不确定性,更重要的是系统通信环节存在着时延,给遥操作系统的控制带来了很大的困难.
很多专家学者对遥操作系统的控制问题进行了深入的研究,取得了一定的研究成果.Raju利用无源性理论来证明了通信环节的有源性会导致整个机器人遥操作系统的不稳定[1].Anderso和Spong基于无源性理论提出了机器人遥操作系统得到了在任意固定时延下系统稳定的控制算法[2].Niemeyer和Slotine在无源性理论的基础上进一步引入波变量的思想,保证了机器人遥操作系统的稳定[3].I.Elhajj等提出了基于事件的控制方法,此方法不直接依赖于时间,所以主从机械手之间的通讯时延不会对系统的稳定性产生任何影响[4-5].预测控制也是一种常见的遥操作系统的控制方法,通过在本地端建立从机械臂的操作模型并以此来补偿时延造成的影响[6-10].这些方法都取得了较好的控制效果,但还是存在着一定的局限性.基于无源性理论的控制方法只能处理固定时延,对时变时延却无能无力.基于事件的控制方法中,事件参考变量的选取主要依靠研究人员的个人经验,目前尚不存在选取事件参考变量的普适方法.预测控制方法的缺点是需要对远端环境进行精确的建模,对远端环境和操作者都要有充分地了解.
针对上述问题,笔者提出了基于H∞控制方法的机器人遥操作系统的同步控制方法.通过设计非线性反馈控制律,定义中间变量和遥操作系统主从机械臂的同步误差变量,将机械臂遥操作系统建模成一类不确定线性时滞系统.基于李雅普诺夫稳定性分析方法和积分不等式方法,给出了系统稳定性和H∞性能分析.最后,基于线性矩阵不等式方法,提出系统的H∞控制器的设计方法.所提出的控制方法可以处理通信环节中的时变时延,适用于时变大时延和有未知外来扰动影响的机械臂遥操作系统,具有一定的鲁棒性.
1问题描述
1.1机械臂遥操作系统的动力学方程
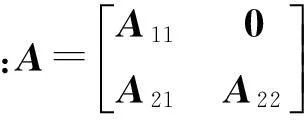
考虑由如下动力学方程描述的机器人遥操作系统:
(1)
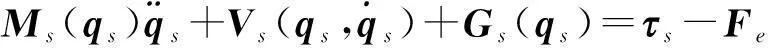
(2)

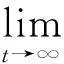
1.2遥操作系统的建模
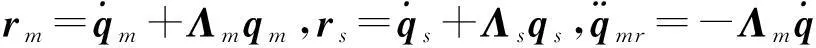
(3)
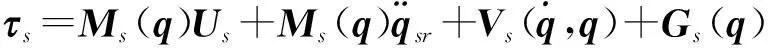
(4)
式中Um=K1rm(t)+K2rs(t-d(t)),Us=K3rm(t-d(t))+K4rs(t)为两个附加的控制变量.
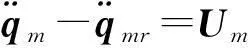
(5)
(6)
定义同步误差信号em(t)=qm(t-d(t))-qs(t)和es(t)=qs(t-d(t))-qm(t).分别对两个同步误差求导,可得
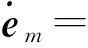
(7)

(8)
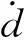
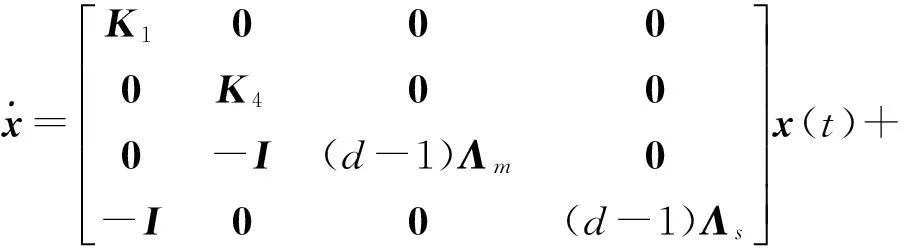
(9)
记Z=[emes]T是系统的被控输出,当Z趋向于零时,机器人遥操作系统的同步误差趋向于零,实现了主从机械臂位置的同步,式(9)简写为
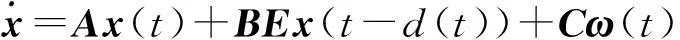
Z=Dx(t)
(10)
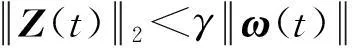
2稳定性和性能分析
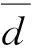
<0
(11)
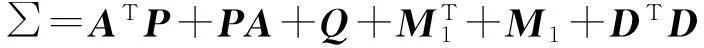
证明:取如下Lyapunov-Krasovskii泛函:
V=V1+V2+V3
(12)
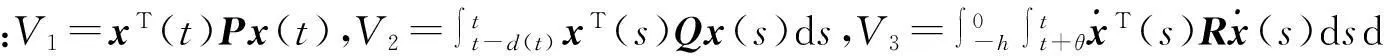
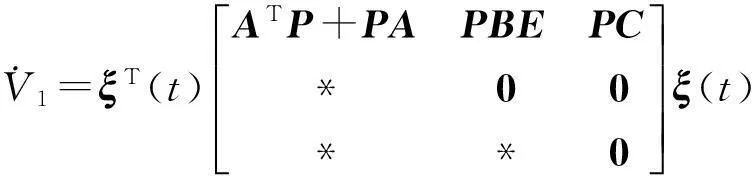
(13)
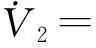
d(t))Qx(t-d(t))=
(14)
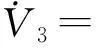
(15)
由文献[12]中的积分不等式可得
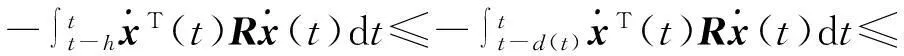
(16)
将式(13~16)分别代入下式:
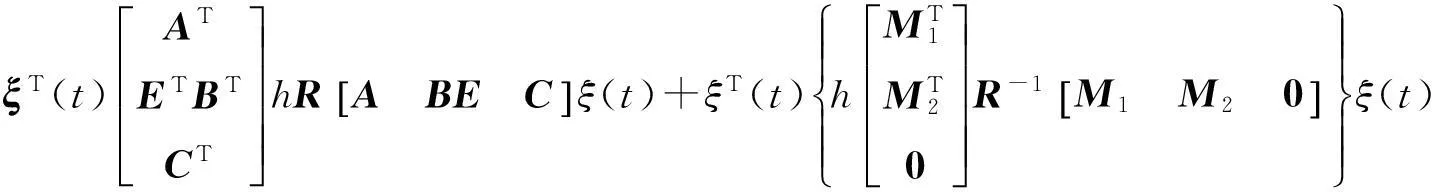
(17)
以下首先证明系统式(10)渐近稳定.此时,令ω(t)=0,由式(11)可得
(18)
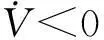
以下证明系统满足H∞性能,令x(t)=0,∀t∈[-h,0].由于
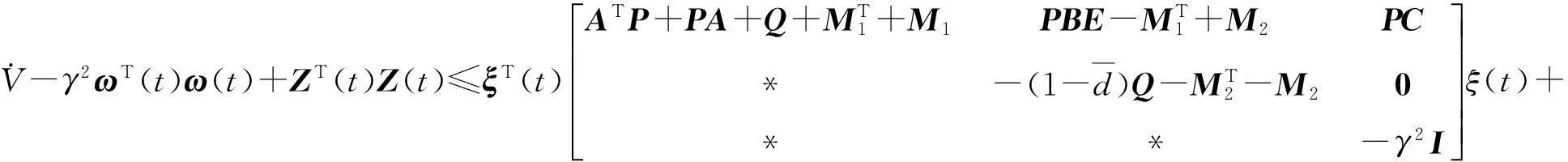
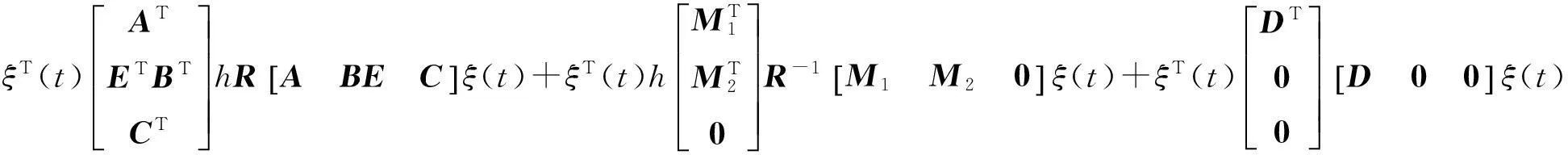
(19)
根据Schur补性质,由式(11)可得
(20)
对上式两端从0到∞进行积分,由零初始条件,可得
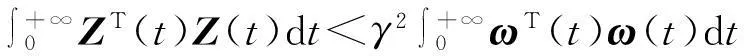
(21)
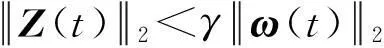
3控制器的设计
以是否依赖时延的大小为依据,稳定性分析分为时滞独立和时滞依赖两类.前面的分析中得到的是时滞依赖的稳定性条件,由于条件和时滞大小有关,具有保守性低的优点,但时滞依赖的稳定性条件往往比较复杂,难以转化为线性矩阵不等式.时滞独立的稳定性条件虽然比较保守,但有其优点:条件一般更加简单,对控制器的设计更为方便.在本节中,将以时滞独立的稳定性条件为基础,采用线性矩阵不等式方法设计H∞控制器.
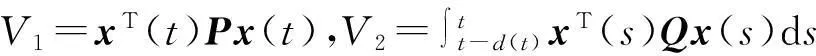
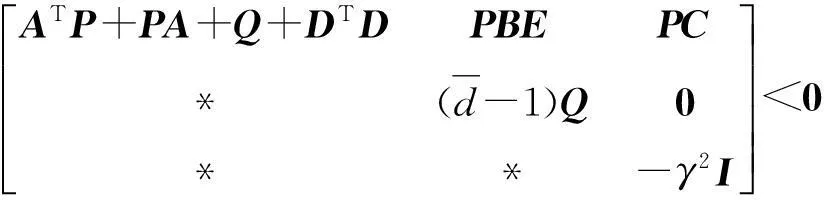
(22)
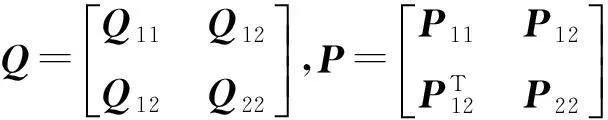

(23)
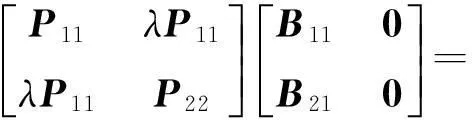
(24)
将式(23,24)代入式(22),并记X=P11A11,Y=P11B11.则式(22)展开变为如下线性矩阵不等式:
(25)
式中∑=X+XT+λP11A21+λA21TP11+Q11.
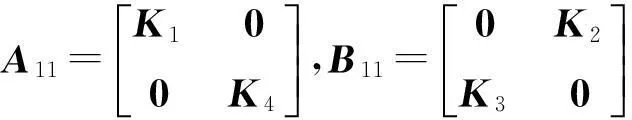
(26)
(27)
用LMI工具箱求解线性矩阵不等式(25)时,可以定义矩阵变量P11,X,Y分别具有上述的块结构,即P11和X具有对角块结构,Y具有反对角块结构.
根据上面的分析,使用LMI工具箱对线性矩阵不等式(25)进行求解,记求得的矩阵变量P11,X,Y分别为
则由式(26,27)可得
K1=Z11-1a,K2=Z22-1c,
K3=Z11-1d,K4=Z22-1b
(28)
4仿真结果
为了验证笔者提出的方法的有效性,在一对两自由度机械臂的遥操作系统上进行仿真验证.选取正定对角系数矩阵Λm=diag[23],Λs=diag[33.5].给定主从机械手的初始位置qm0=[0.50.2]T,qs0=[0.70.8]T,则中间变量rm和rs的初始值rm0=[10.6],rs0=[2.12.8],误差信号的初始值em0=[-0.2-0.6],es0=[0.20.6].选取通讯环节时延d(t)=1+0.3sin(t),时延变化率的确定部分d取时延变化率的平均0,H∞控制性能指标γ=3.
采用笔者提出的基于H∞控制的机器人遥操作系统同步控制方法,参数λ取1,运用MATLAB的LMI工具箱求解线性矩阵不等式(25),可以得到t=-0.090 648<0.说明式(25)存在可行性解.可分别求得矩阵X,Y,P11,P22为
X=diag〔-15.442-15.482-16.346-15.722〕

P11=diag〔2.4031.5841.561.336〕.
由前面得到的H∞控制器的设计方法可得
K1=diag〔-6.424-9.774〕
K2=diag〔-0.6470.079〕
K3=diag〔0.5540.424〕
K4=diag〔-10.478-11.761〕.
为了和本节提出的机器人遥操作系统同步控制的控制效果进行对比,采用文献[13]提出的基于时变时延以及线性逼近的自适应控制方法对上述遥操作系统进行同步控制,其仿真算例中选取的控制器参数分别为
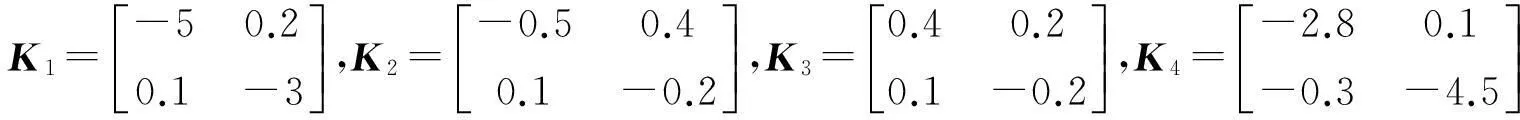
仿真结果如图1~4所示.
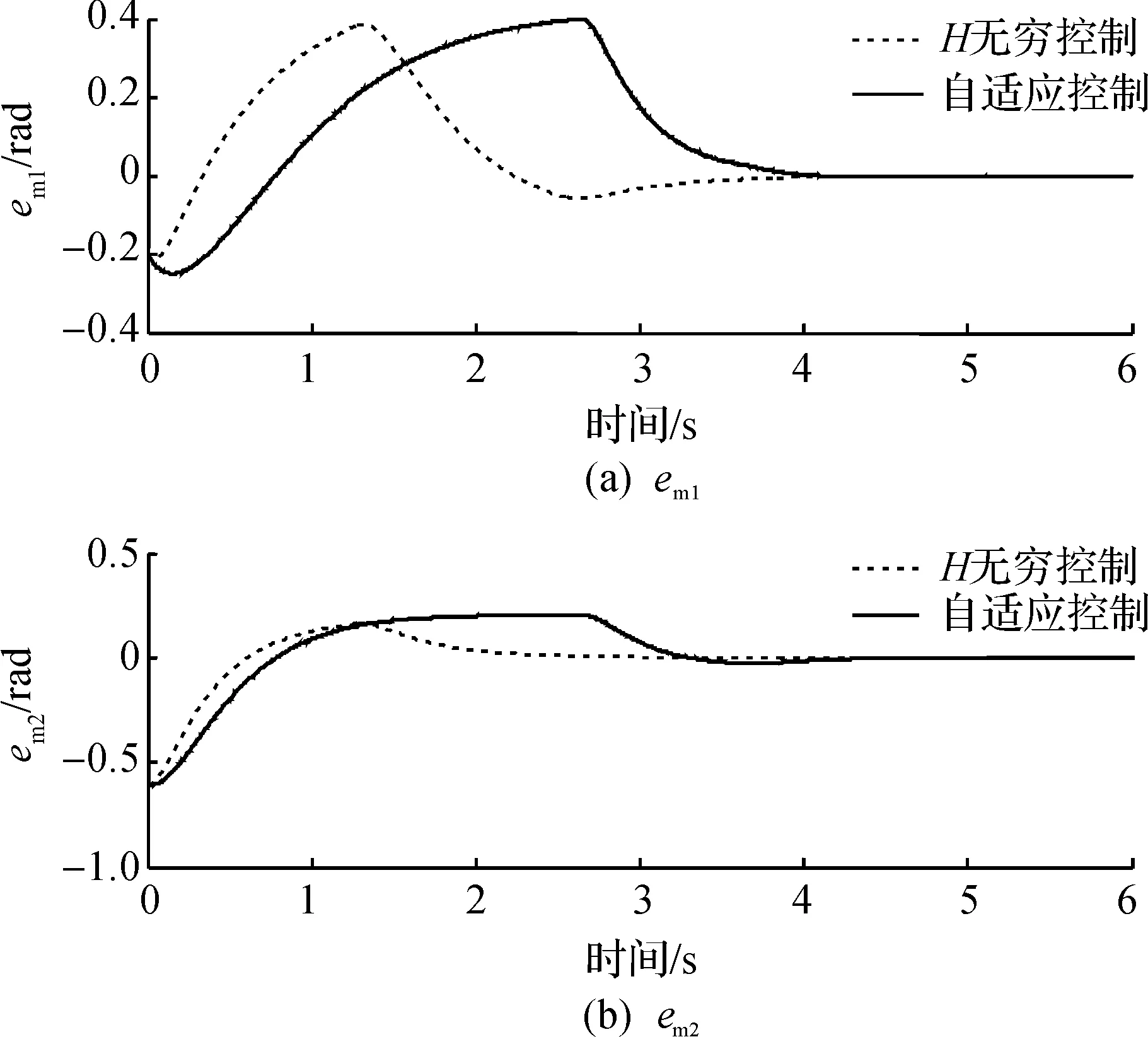
图1 主机械臂同步误差em状态曲线Fig.1 State trajectory of master manipulator synchronizationerrors em

图2 从机械臂同步误差es状态曲线Fig.2 State trajectory of slave manipulator synchronizationerrors es
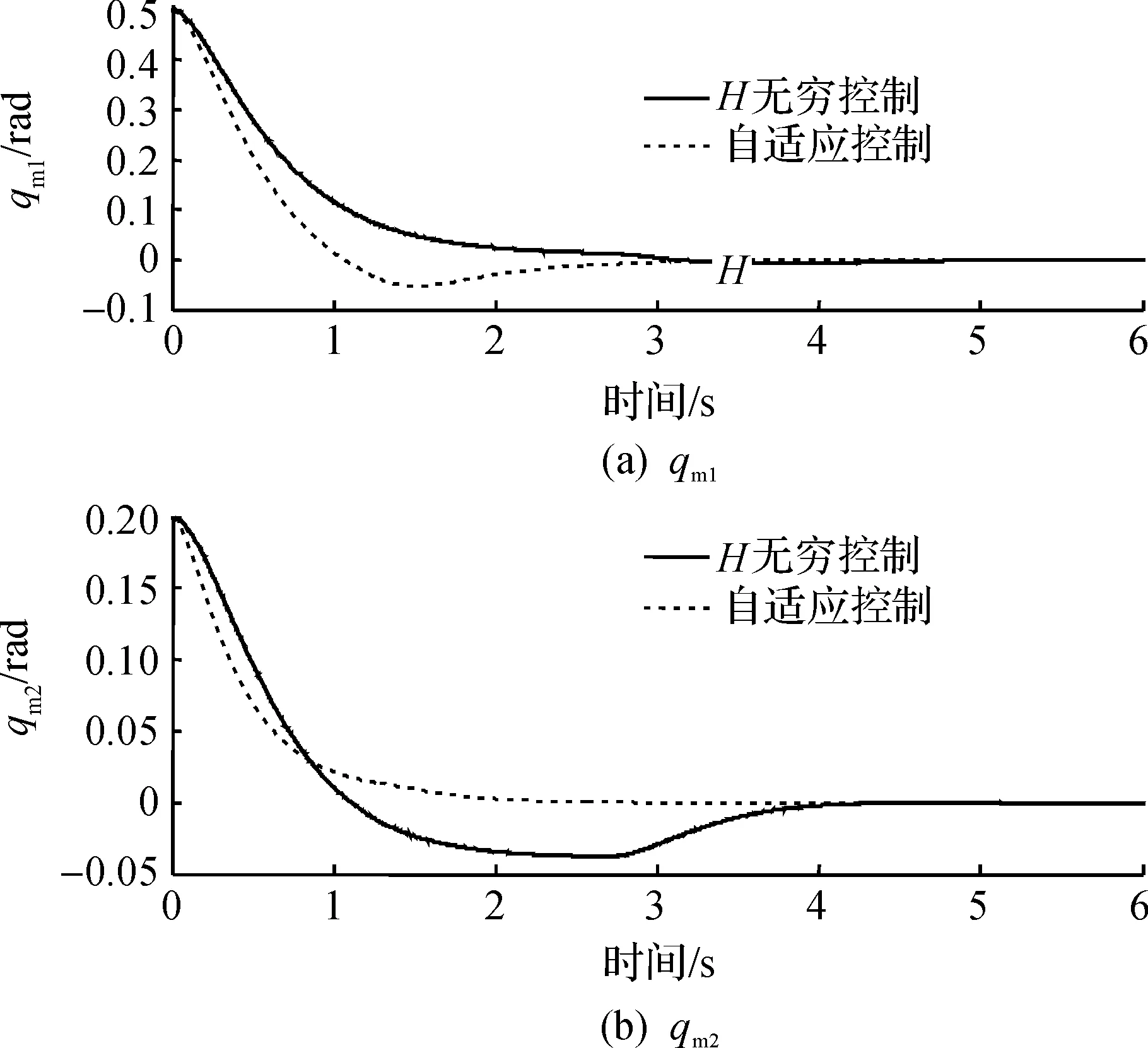
图3 主机械臂位置qm状态曲线Fig.3 State trajectory of master manipulator position qm
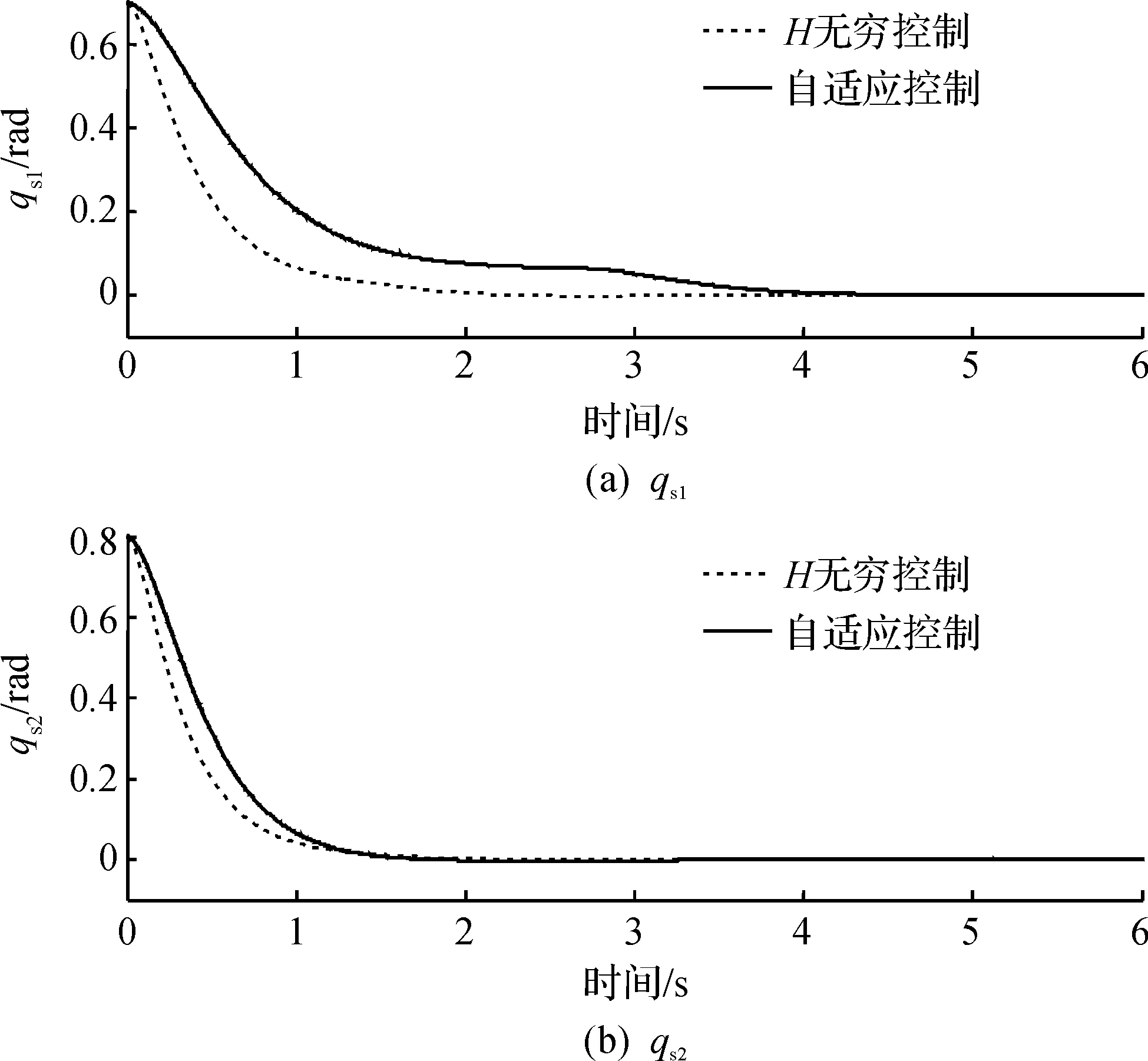
图4 从机械臂位置qs状态曲线Fig.4 State trajectory of slave manipulator position qs
由以上的仿真结果可以得到:基于H∞控制方法的机器人遥操作系统的同步控制方法和文献[13]提出的自适应控制方法都能够保证整个机器人遥操作系统渐近稳定,并且实现机器人遥操作主从两端关节位置的同步.且本节提出的同步控制方法比文献[13]提出的自适应控制方法具有更好的动态特性,同步误差能够较快趋于零,关节位置能够更加快速的趋于稳态.这是由于在遥操作系统的不确定性线性时滞系统的构建中,其中的不确定性用于描述时变时延引起的系统动态,本节提出的同步控制方法能使系统的不确定性对系统的影响尽可能小.
5结论
针对具有时变大时延的机器人遥操作系统,提出了一种基于H∞控制的同步控制方法.该控制方法可以处理通信环节存在时变时延的机器人遥操作系统,实现主从机械臂位置的同步,仿真结果表明了方法的有效性.
参考文献:
[1]RAJUGJ.Operatoradjustableimpedanceinbilateralremotemanipulation[D].Boston:MassachusettsInstituteofTechnology,1988.
[2]ANDERSONR,SPONGMW.Bilateralcontrolofteleoperatorswithtimedelay[J].AutomaticControl,1989,34(5):494-501.
[3]NIEMEYERG,SLOTINEJJE.Stableadaptiveteleoperation[J].OceanicEngineering,1991,16(1):152-162.
[4]ELHAJJI,XIN,FUNGWK.Hapticinformationininternet-basedteleoperation[J].Mechatronics,2001,6(3):295-304.
[5]ELHAJJI,XIN.Real-timecontrolofInternetbasedteleoperationwithforcereflection[C]//Proceedingsofthe2000IEEEInternationalConferenceonRoboticsandAutomation.SanFrancisco:IEEE,2000:3284-3289.
[6]陈启宏,费树岷,宋爱国.遥操作机器人系统的预测控制[J].东南大学学报:自然科学版,2003,33(2):177-181.
[7]杨马英,俞立,张美玉,等.约束预测控制的可行解与稳定性[J].浙江工业大学学报,1999,27(3):187-194.
[8]陆冬娜,杨马英.基于RBF神经网络的非线性模型预测控制[J].浙江工业大学学报,2007,35(2):123-126.
[9]BURDEAGC.Invitedreview:thesynergybetweenvirtualrealityandrobotics[J].RoboticsandAutomation,1999,15(3):400-410.
[10]BARTHM,BURKERTT,EBERSTC,etal.Photo-realisticscenepredictionofpartiallyunknownenvironmentsforthecompensationoftimedelaysintelepresenceapplications[C]//Proceedingsofthe2000IEEEInternationalConferenceonRoboticsandAutomation.SanFrancisco:IEEE,2000:3132-3137.
[11]CHOPRAN,SPONGMW,LOZANOR.Synchronizationofbilateralteleoperatorswithtimedelay[J].Automatica,2008,44(8):2142-2148.
[12]ZHANGX,WUM,SHEJ,etal.Delay-dependentstabilizationoflinearsystemswithtime-varyingstateandinputdelays[J].Automatica,2005,41:1405-1412.
[13]曹晓青.基于网络时延的遥操作机器人控制研究[D]. 上海:上海交通大学,2012.
(责任编辑:陈石平)
文章编号:1006-4303(2015)06-0649-06
中图分类号:TP241
文献标志码:A
作者简介:张文安(1982—),男,浙江洞头人,教授,博士,研究方向为信息融合与网络化控制,E-mail:wazhang@zjut.edu.en.
基金项目:国家自然科学基金资助项目(61202203)
收稿日期:2015-05-06
