基于射线理论的海洋中尺度涡与水声传播耦合建模研究

高太长，男，教授，博士生导师。

基于射线理论的海洋中尺度涡与水声传播耦合建模研究

程天际1，艾锐峰2，张建伟2，高太长1，欧阳军2

(1. 解放军理工大学 气象海洋学院， 江苏 南京 211101；2. 中国白城兵器试验中心， 吉林 白城 137001)

摘要针对涡旋场景下水声传播特性预报问题，基于射线方法，研究了中尺度海洋涡旋与水声传播的耦合建模方法。该方法首先根据涡旋的基本特性，建立涡旋区域的温度场分布模型和水介质运动速度模型；由Mackenzie公式，计算声速分布；然后运用动态射线寻迹方法，建立水声传播模型，从而实现海洋学模型与水声传播模型的耦合。仿真分析表明：可以用它进行涡旋影响下水声传播规律的预报，并进而指导舰(潜)艇的战术动作。

关键词水声传播；中尺度涡；耦合建模；射线寻迹

作者简介程天际(1991-)，男，硕士研究生，主要研究方向为海洋探测。cheng_tianji@163.com

中图分类号P733.21

文章编号2095-3828(2015)06-0114-06

文献标志码A

DOI10.3783/j.issn.2095-3828.2015.06.025

AbstractAiming at prediction of underwater acoustic propagation characteristics in the scene of eddy, based on the ray method, the paper researches the coupling modeling method of mesoscale eddy and underwater acoustic propagation. Basic principles of this method are that, first of all, according to the basic property of eddy, establish the temperature field distribution model and moving speed model of water medium in eddy area; calculate acoustic speed distribution with Mackenzie equation; and then with dynamic ray tracing method, establish an underwater acoustic propagation model to realize the couple between oceanographic model and underwater acoustic propagation model. Simulation analysis shows that it can be used to predict the law of underwater acoustic propagation influenced by eddy and to instruct the tactical operation of the surface warship or submarine.

Keywordsunderwater acoustic propagation; mesoscale eddy; couple modeling; ray tracing

Couple Modeling of Mesoscale Eddy and

Underwater Acoustic Propagation Based on Ray Theory

CHENG Tianji1，AI Ruifeng2，ZHANG Jianwei2，GAO Taichang1，OU Yangjun2

(1. College of Meteorology and Oceanography, PLA University of Science &Technology, Nanjing Jiangsu 211101, China;

2. China Baicheng Ordnance Test Center, Baicheng Jilin 137001, China)

中尺度涡是海洋中的相干旋转水体，类似大气中的气旋或风暴，常伴随着洋流而产生，是海洋中普遍存在的现象[1]。涡旋对水声传播的影响主要体现为对声速剖面分布的改变及介质的运动效应。分析涡旋场景下的水声传播规律，对预报声呐的探测性能，规划潜艇的战术动作，具有重要意义[2]83。

目前，利用测量方法难以全面而实时地获取涡旋的特征数据[3]。根据传感器测量数据，结合历史数据，融合涡旋特征模式，建立数学预报模型，更加快捷而实用[4]37-38。对于水声传播计算而言，根据对波动方程的假设和近似的不同，主要分为射线理论模型、简正波模型、抛物方程模型、多途扩展模型、快速场模型，以及一些混合算法[5]。

建立海洋学和水声学的耦合模型，一方面可以通过水声传播特性的分析反向研究海洋现象；另一方面可以作为战术环境支持系统，指导复杂海洋水文条件下的海军作战(声呐的战术使用，潜艇的战术机动)。美军利用动力学海洋模型结合水声传播模型进行反潜作战期间的海上力量部署[2]83-85。文献[4]39-46和文献[6]中利用抛物方程模型对中尺度涡的水声传播特性进行了研究，没有考虑涡旋运动对声波传播的影响。考虑到介质的运动效应以及声呐工作频段的实际情况，抛物方程模型难以适应。射线声学物理意义明确，计算速度快，能够以射线寻迹的方式实现对介质运动的跟随，且更适应目前的声呐工作频段。因而，本文基于射线理论对中尺度涡和水声传播进行耦合建模。

1中尺度涡和水声传播的耦合建模

1.1　中尺度涡现象及数学模型

海洋中尺度涡是叠加在海洋平均流场上，空间水平尺度在几十千米至几百千米之间的涡旋，是重要的海洋动力现象。其存在时间为数天至数月。它与海洋中大而稳定的环流相比，是局部现象。但是在近海，其尺度十分可观，对于海军战场环境有重要影响。涡旋的产生机理比较复杂，没有定论。海面风的作用、洋流的蛇行、地形作用、海面加热和冷却都可能导致涡旋。

涡旋按照自转方向可分为2种类型：(1) 按逆时针旋转的气旋式涡旋，为冷水团，其中心海水自下向上运动，涡旋内部水温比周围海水温度低，称为冷涡；(2) 按顺时针旋转的反气旋式涡旋，为热水团，其中心海水自上向下运动，携带上层的暖水进入下层冷水中，涡旋内部水温比周围水温高，称为暖涡。

1936年，Iselin观测到墨西哥湾中的一种大尺度的水温异常现象，经过近10 a的观测与分析，于1948年证实了此种温度异常水团存在着转动运动，从而开启了中尺度海洋涡的研究。1981年9月至1982年7月，美国“暖涡旋计划”(Warm Core Rings Program)利用红外观测，对美国东北部湾流中的涡旋现象进行了调查。基于调查资料，海洋学家对湾流附近的中尺度涡进行了一系列分析，揭示了湾流中尺度涡的形成、演变机理，其温盐场分布、流场结构及动力机制。我国于20世纪80年代末，对东海南部、南海以及西太平洋边缘区域的中尺度涡现象进行了调查研究。

基于海洋调查研究，海洋学界对中尺度涡的运动规律和动力机制有了一定的认识。但受观测方法和手段的限制，这些研究大多局限于对少量观测现象的描述，对涡旋产生过程、运动轨迹以及与周围海水相互作用没有足够的分析。卫星和遥感手段的运用，使得可以大范围、长时间的对涡旋进行观测，推进了对其机理的研究，但是无法深入到海洋内部。利用观测资料，结合数值模拟，建立数学模型的研究方式成为一种主要的手段。同时，所构建的数学模型能够为实际应用提供便利。

涡旋会对海水温度、盐度的分布产生扰动，它会促成海水的混合，通过海水的上下运动输送营养盐，并且引起海域水体的物质、能量交换。考察它对水声传播的影响，主要需考虑的是对温度场的扰动效应及对水介质运动的影响。

一般可以通过卫星遥感等测量方式获得涡旋的特征参数：中心位置[x0(z),y0(z)]、水平空间尺度[xR(z),yR(z)]、分布深度[zDmin(z),zDmax(z)]。据此，可以建立涡旋的数学模型，如式(1)所示。

(1)

式中,zDmin≤z≤zDmax；0≤γ(x,y)≤1；x0(z)-|xR(z)·γ(x,y)|≤x≤x0(z)+|xR(z)·γ(x,y)|；y0(z)-|yR(z)·γ(x,y)|≤y≤y0(z)+|yR(z)·γ(x,y)|。

设涡旋中心温度为Tc，边缘温度为TB，涡旋区域以外的温度为环境温度T0。假设温度从中心到边缘线性变化，则可以通过线性插值得到温度场分布，如式(2)所示。

(2)

对于实际中的海水涡旋，受各种环境因素的影响，会使其形状及温度产生变化，涡旋不一定满足式(1)的规则形状，而且温度从中心到边缘的变化也不一定是线性的，因此需在解析模型上叠加一个满足正态分布的随机扰动ΔT，如式(3)所示。

(3)

涡旋从产生之时起就不停地运动，其运动可分为自转、平移和垂直3种方式。对于水声传播而言，暂时不考虑垂直运动。以涡旋的中心为观察点(r,α,z)，可以将涡旋的运动(自转和平移)分解为切线方向的切向流速Vα和直径方向的径向流速Vr。

在文献[7]中对切向流速Vα进行了研究，给出了变化规律。它将中尺度涡分为内区和剪切区。设rmax为涡旋切向速度由最大值过渡到背景流场时相对于涡旋中心的距离，则内区为0≤r≤rχ,剪切区为rχ≤r≤rmax。本文采用一个简单的模型，如式(4)所示。

(4)

式中,V0、β为系数；F0(z)为切向速度随水深变化的描述函数。径向流速Vr一般较小，相对声呐的工作频段而言，可以将其忽略。

至此，得到了涡旋对温度场扰动的数学模型及其水介质的运动规律描述。

1.2　声线方程

设声源位于x0(x,y,z)，基于射线理论，可以得到用以描述声场的声线方程，如式(5)所示。

(5)

式中,ξ(s)、η(s)、ζ(s)为中间函数；s为声线弧长；[x(s),y(s),z(s)]表示声线轨迹。

解式(5)，可以得到声线的轨迹[x(s),y(s),z(s)]。

通过对声线的寻迹，可以得到声波的传播时延及声波幅度随声线的变化。如式(6)、式(7)所示。

(6)

(7)

式中,J(s)为雅克比行列式。

于是，可以将谐和点声源的声压场表示为

(8)

1.3　耦合建模

中尺度涡对水声传播的影响体现在2个方面：一是通过对温度场的扰动影响水体中的声速分布；二是涡旋的运动使得声波的传播介质附加了一个运动效应。

声速可以表示为水温、盐度和压力(深度)的函数，一般可以根据经验公式进行计算。常用的Mackenzie公式如式(9)所示。

c=1 448.96+4.591T-5.304×10-2T2+

2.374×10-4T3+1.340(S-35)+

1.630×10-2D+1.675×10-7D2-

1.025×10-2T(S-35)-7.139×10-13TD3

(9)

式中,D为水深；S为盐度，根据海区历史数据或者现场数据，给出其估计值，并假定涡旋区域盐度值在水声传播期间不变化；水温T由式(3)所示模型进行计算，从而可以由涡旋的数学模型及其特征参数推算出声速分布c(X)。

一般而言，可以根据声场分布c(X)，计算声线轨迹。但是由于涡旋的运动，作为声传播介质的水体具有一定的速度，因此需要对内容进行改进。下面根据射线理论，考虑介质运动(涡旋运动造成)，建立射线寻迹方程。如图1所示。

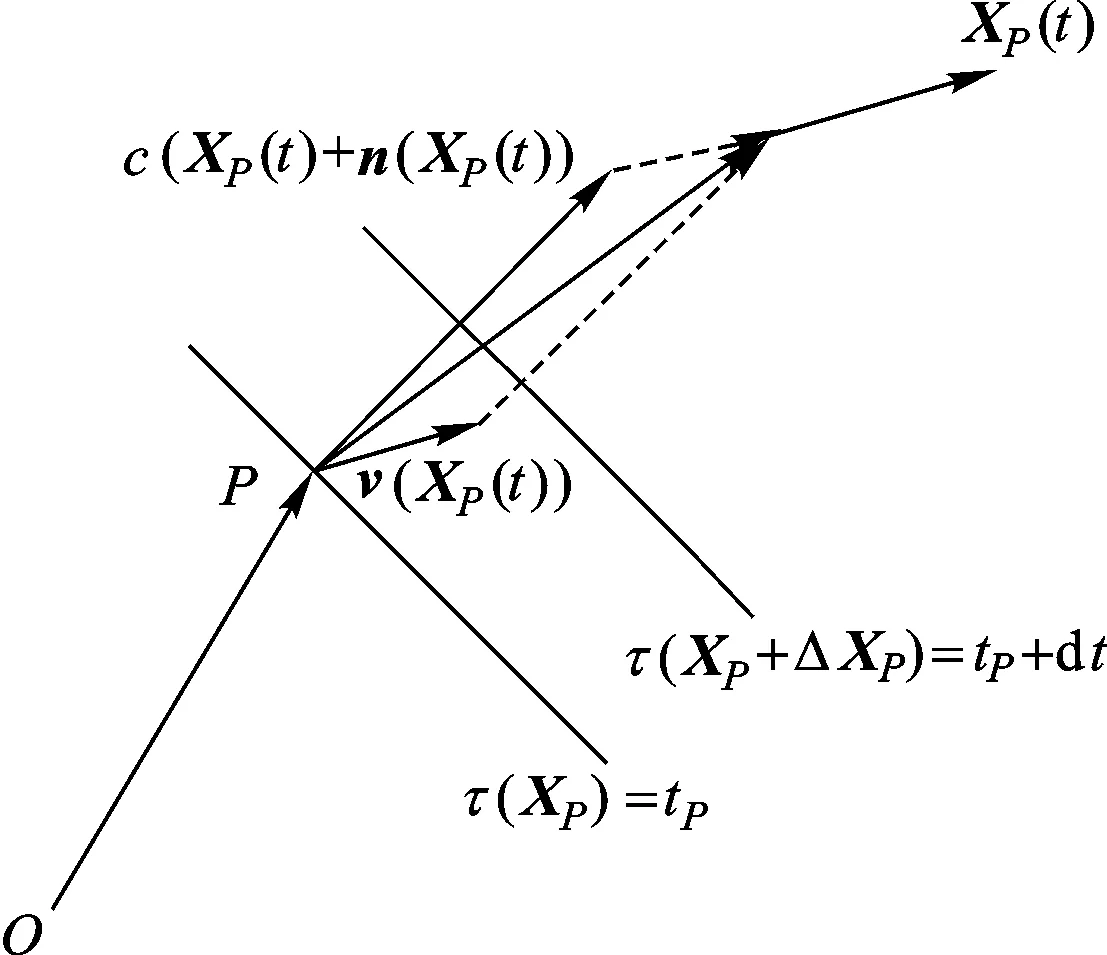
图1　射线寻迹示意图

图1中，τ(X)=tP为波阵面，点XP(t)以速度vray(XP(t))传播，形成一条从源点O出射的声线轨迹。速度vray(XP(t))由两部分合成：c(XP(t))n(XP(t))为波速(n(XP(t))为波阵面法向矢量)；v(XP(t))为介质运动速度(涡旋运动速度)。

由图1可知：

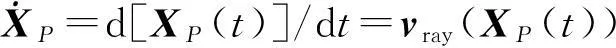
(10)

再推导a(XP(t))沿射线轨迹的时间变化率的微分方程[8-9]

(11)

给出声速分布c(X)，涡旋中水介质速度v(X)，则可以利用式(10)、式(11)进行射线寻迹。显然，通过寻迹可以直接得到τ(s)。

对于幅度的求解，涡旋中水介质速度v(X)的作用可以忽略。但是传统的射线方法存在着固有的缺陷，难以较好地处理影区和焦散区的声场计算。将射线跟踪改进为波束跟踪能实现影区和焦散区声场的平滑过渡[10]。

根据中心射线声压幅值计算方法以及邻域内声压分布规律的不同，波束跟踪可分为有限元波束跟踪[11]、高斯波束跟踪等方法[12-13]。其基本原理都是通过求解动态射线方程以得到中心射线上的声强，然后按照一定的分布规律计算波束范围内其他点的声场值。

引入新的坐标系(s,m)(s为沿着射线的弧长，m为距波束中心射线的法向距离)，根据文献[14]得到声压方程

(12)

式中，A(s)为沿中心声线的幅度;ψ(s,m)表示波束范围内声场的分布规律。

通过对到达接收点所有波束贡献的求和，可以得到接收点的声场

(13)

2仿真试验与应用场景分析

利用上述模型进行涡旋场景下的水声传播特性预报的步骤如下：

1) 根据涡旋特征参数[x0(z),y0(z)]、[xR(z),yR(z)]、[zDmin(z),zDmax(z)]，利用式(1)计算涡旋形状；

2) 根据式(1)计算结果，利用公式(4)计算温度场分布T(X)；

3) 依据温度场分布T(X)，由Mackenzie公式计算出声速场分布c(X)；利用式(4)计算涡旋中水介质速度v(X);

4) 利用式(10)、式(11)进行射线寻迹，导出c(X)、v(X)下的声线轨迹，并计算出声线各点时延τ(s)；

5) 运用高斯波束跟踪方法，由式(12)计算跟踪波束的声压，再由式(13)计算接收点的声场声压。

下面依据上述步骤，进行仿真试验。

为了便于比较无涡旋、暖涡旋、冷涡旋下的结果，给定深度点Zd=[0 10 50 100 200 300 400]；统一设置环境温度T0=[18 16 12 11 10.5 10 9.4]；盐度S=32。

试验1暖涡

参数设置：涡旋中心位置(x0,y0)，x0=[0 0 300 1 0001 0001 5002 000] ，y0=[0 0 -400 -200 200 1 000 2 000]；水平尺度(xR,yR)，xR =[900 1 00015 00018 00015 00020 0001 000]，yR =[650 600 10 00013 00017 00018 0001 300]；涡旋中心温度Tc=[22 21 17 15 14 13 12]；涡旋边缘温度TB=[18 16 12 11 10.5 10 9.4]。

其温度场及对应的声速分布如图2所示。

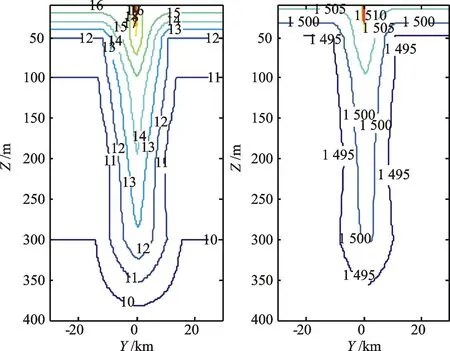
a) 暖涡温度场分布图b) 暖涡声速分布图 图2　暖涡温度场、声速场分布

试验2冷涡

参数设置：涡旋中心位置(x0,y0)，x0=[0 0 300 1 000 1 000 1 500 2 000] ，y0=[0 0 -400 -200 200 1 000 2 000]；水平尺度(xR,yR)，xR =[900 1 00015 00018 00015 00020 0001 000]T，yR =[650 600 10 00013 00017 00018 0001 300]T；涡旋中心温度Tc= [14 11 9 8.5 8 7 6]；涡旋边缘温度TB= [16 12 11 10.5 10 9.4]。

其温度场及对应的声速分布如图3所示。

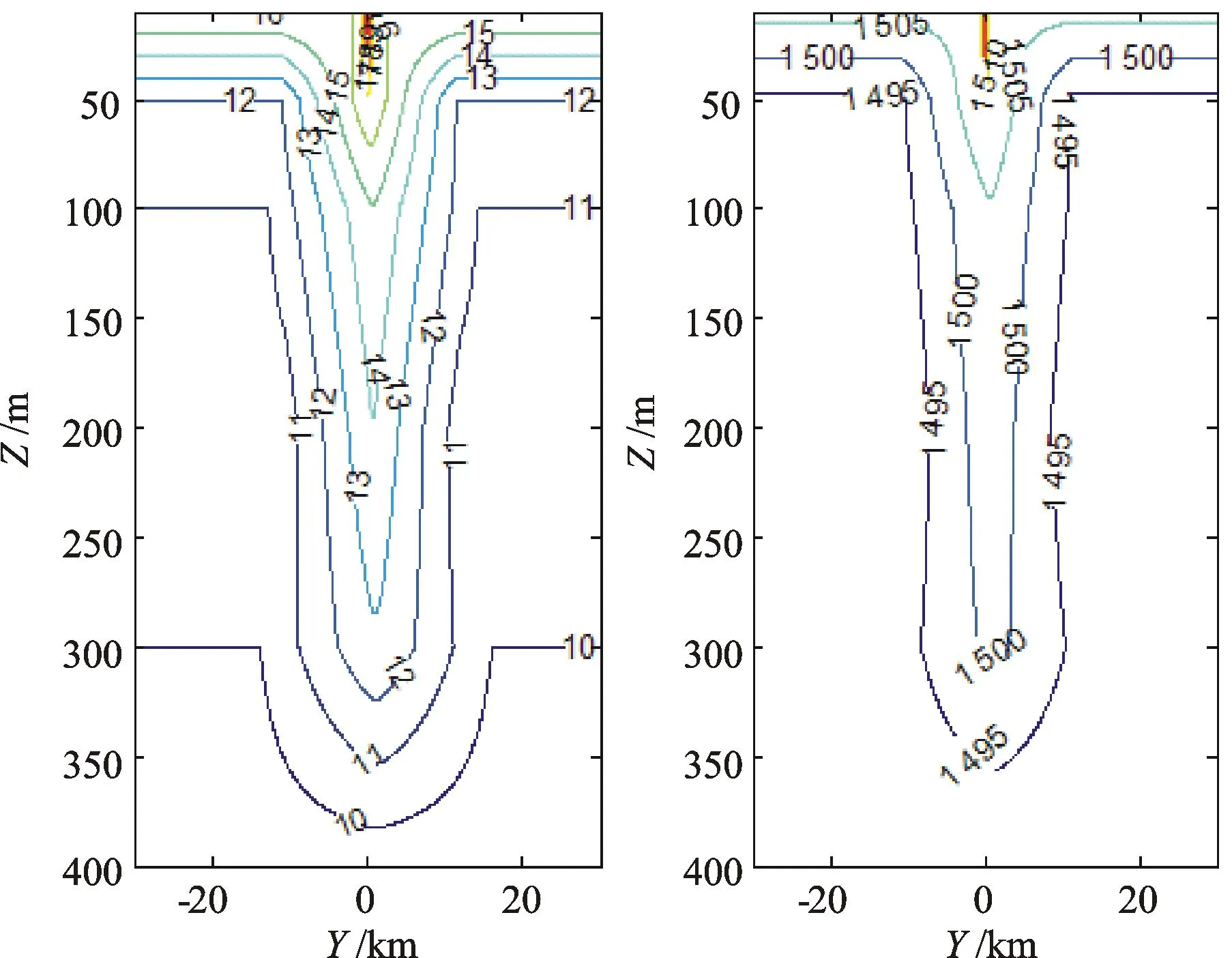
a) 冷涡温度场分布图b) 冷涡声速分布图 图3　冷涡温度场、声速场分布

试验3水声传播计算

将上述仿真结果输入到水声传播模型中(射线寻迹方程)，比较无涡旋、暖涡旋、冷涡旋下的结果。将声源设定在涡旋中心，深度为900 m处。图4、图5、图6分别是无涡旋、暖涡旋、冷涡旋下声线轨迹图和声压场的仿真结果。

a) 无涡旋下声线轨迹图

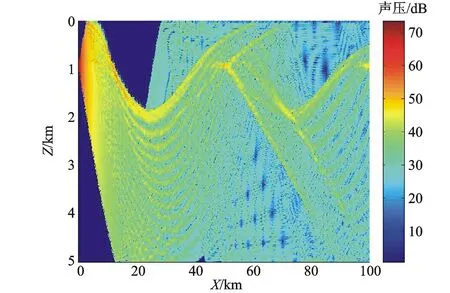
b) 无涡旋下声压场 图4　无涡旋

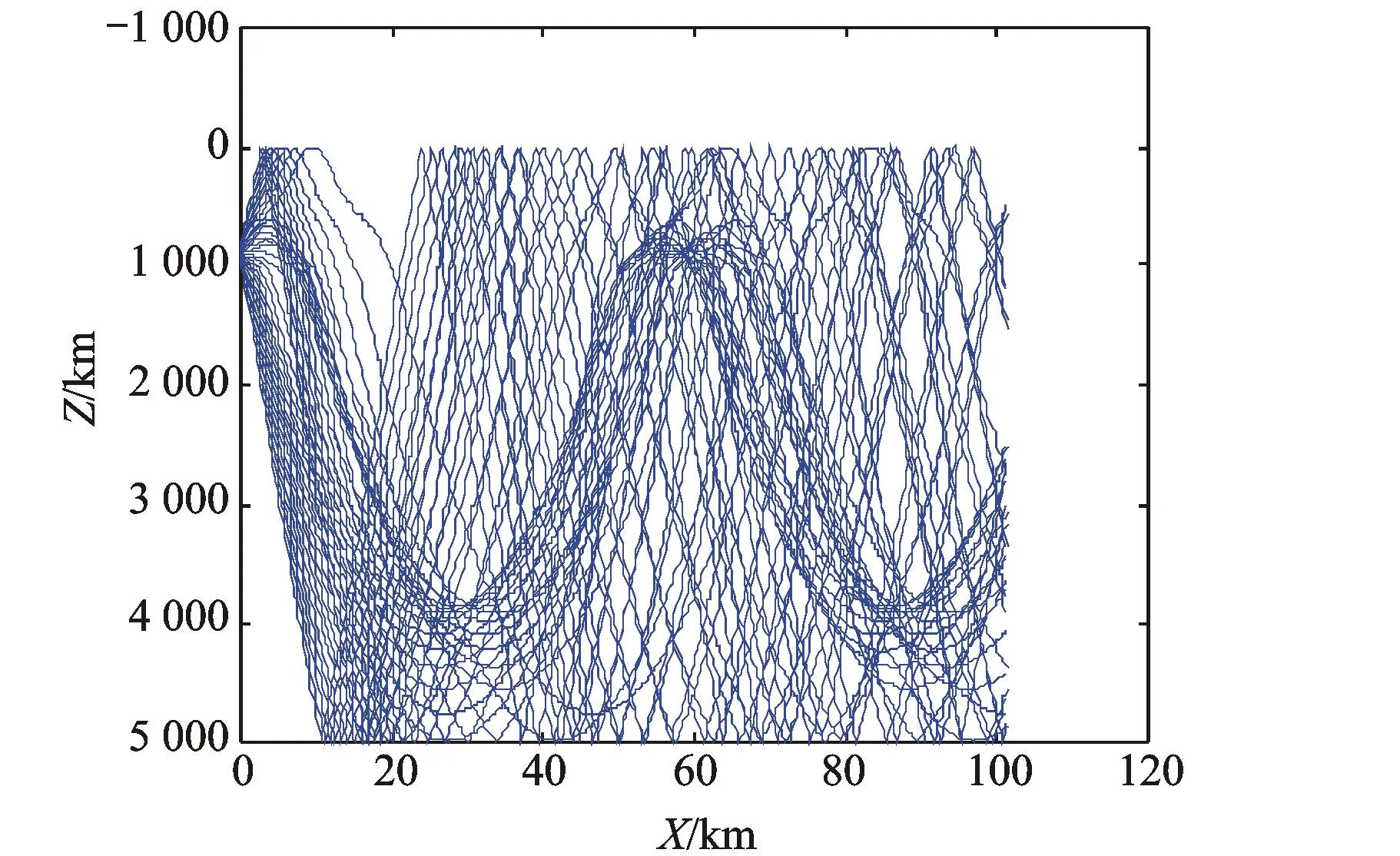
a) 暖涡旋下声线轨迹图

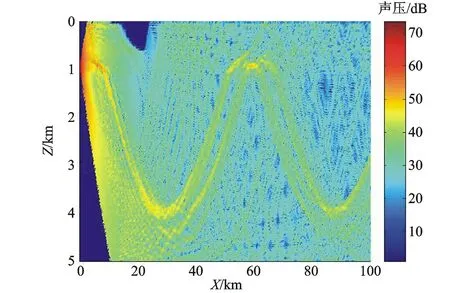
b) 暖涡旋下声压场 图5　暖涡

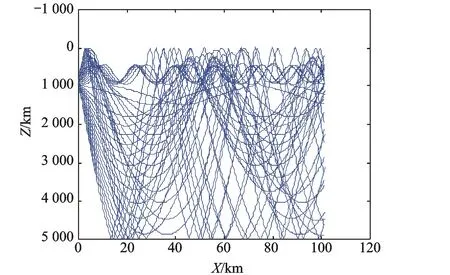
a) 冷涡旋下声线轨迹图

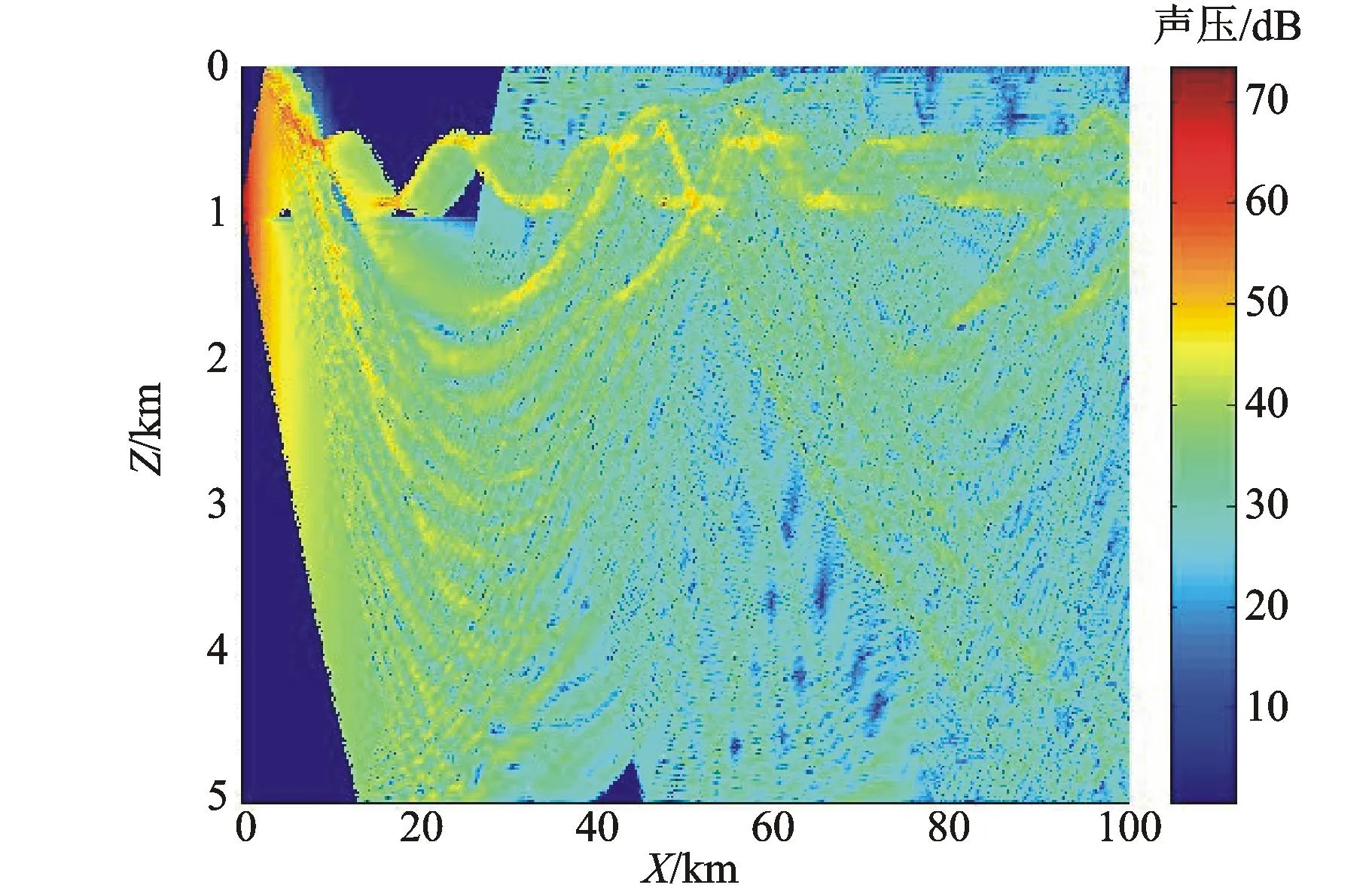
b) 冷涡旋下声压场 图6　冷涡

比较暖涡与无涡时的声线轨迹和声压场，可以发现，暖涡对汇聚区有一个下压效应，从而导致声呐对此一区域近海面目标探测能力的下降。而冷涡旋时，在近程距离上，相对无涡旋时，声波会产生向下折射效应。总之，由于冷涡旋和暖涡旋对声速场的改变，将改变声压场的分布，于是在作战中可以通过耦合模型通过声压场的预报，采取相对有利的战术机动动作。

试验4应用场景分析

根据上述仿真结果，以冷涡为例。潜艇在航行中如果能够进入冷涡，并下潜至冷涡深度中部，则潜艇所辐射的声波会向下折射，从而可以一定程度上规避水面舰艇的探测。如图(7)所示。

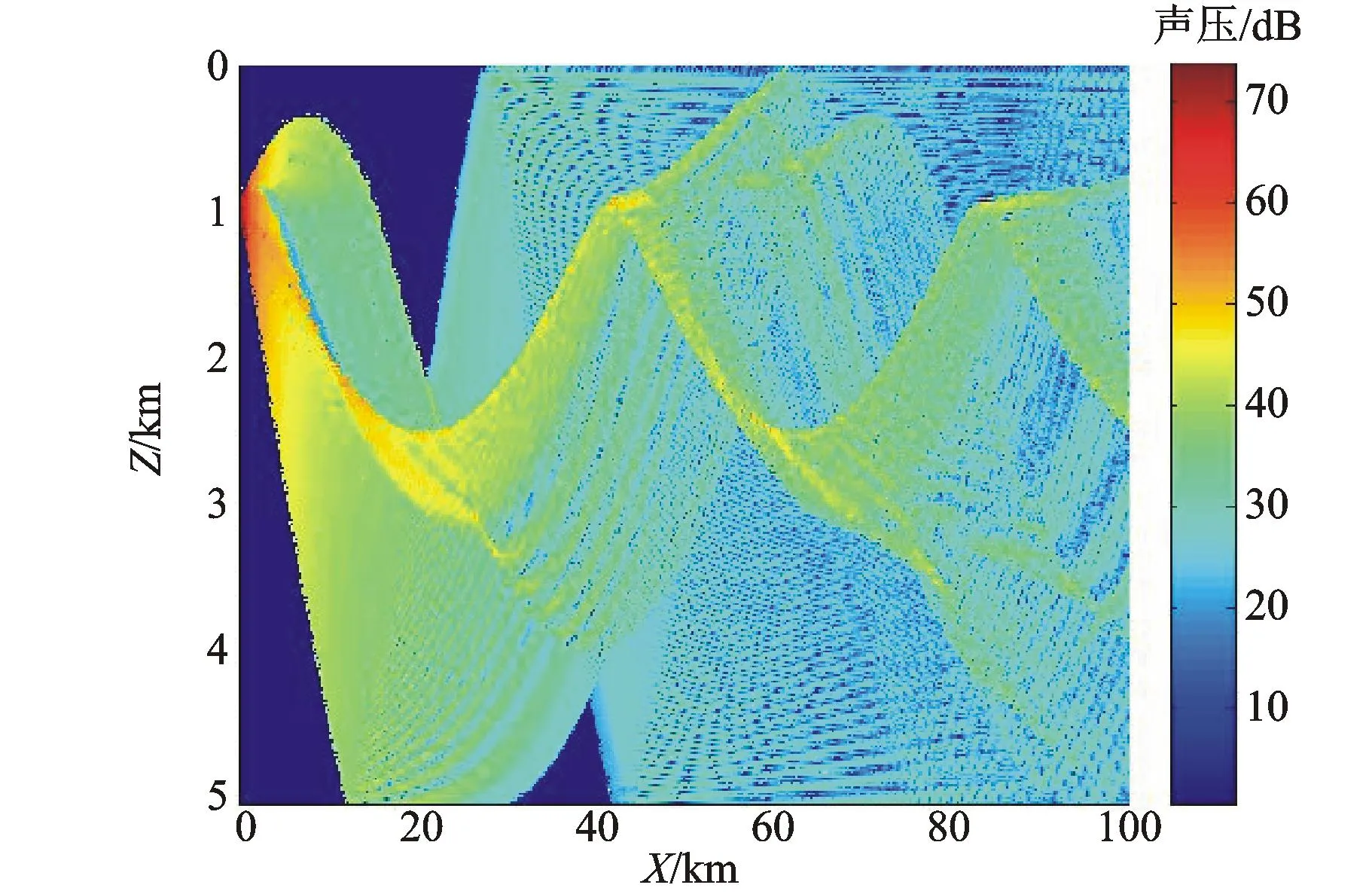
图7　潜艇利用冷涡规避探测

3结 束 语

本文将海洋中尺度涡模型与水声传播模型相融合，运用射线寻迹的方法，构造了二者之间的耦合模型。它既考虑了涡旋导致温度场改变对声速分布的影响，又考虑了涡旋运动导致海水介质附加速度对声传播的影响，能够较好地刻画涡旋对水声传播的影响。根据此模型，对涡旋场景下的水声传播规律进行了仿真试验研究。结果表明，可以通过模型计算的方式，对水声场进行预报，从而指导舰(潜)艇的战术动作，以更好的探测目标或者规避探测。

参考文献(References)

[1]孙文心,李凤岐,李磊.军事海洋学引论[M].北京:海洋出版社,2011：132-136.

[2]ETTER P C.Underwater acoustic modeling[M].London:Elsevier Applied Science,1991.

[3]赵骞,田纪伟,褚忠信,等.渤海、黄海、东海海流场和温度场的数值同化研究[J].武汉理工大学学报,2006(6):821-825.

[4]李佳讯,张韧,陈奕德,等.海洋中尺度涡建模及其在水声传播影响研究中的应用[J].海洋通报,2011,30(1):37-46.

[5]JENSEN F B,PORTER M B.Computational ocean acoustics[M].New York:AIP Press,1993：103-170.

[6]刘清宇.海洋中尺度现象下的声传播研究[D].哈尔滨:哈尔滨工程大学，2006：23-56.

[7]徐青.中尺度涡诱导的海洋内波动力学研究和海洋遥感高新技术探索[D].青岛:中国海洋大学,2007：17-35.

[8]ENGELKE R.Ray trace acoustics in unsteady inhomogeneous flow[J].J.Acoust.Soc.Am,1974,56(4):1291.

[9]UGINCIUS P.Ray acoustics and Fermat’s principle in a moving inhomogeneous medium[J].J.Acoust.Soc.Am.,1972,51(5):1759.

[10]CERVENY V,POPOV M M,PSECIK I.Computation of wave fileds in inhomogeneous media-Gaussian beam approach [J].Geophys,J.R.astr.Soc.,1982,70:109-128.

[11]PORTER M B,LIU Y C,Finite element ray tracing [J].Theoretical and Computational Acoustics,1994,2:947-956.

[12]WEINBERG H,KEENAN R E.Gaussian ray bundles for modeling high-frequency propagation loss under shallow-water conditions[J].J.Acoust.Soc.Am.,1996,100(3):1421-1431.

[13]BUEKER H.A simple 3-D Gaussian beam sound propagation model for shallow water [J].J.Acoust.Soc.Am.,1994,95(6):2437-2440.

[14]姚万军.水声场计算模型与声呐性能分析方法研究[D].武汉:海军工程大学，2008：23-48.

(编辑：李江涛)