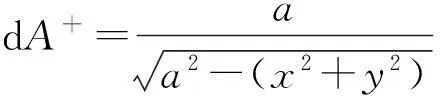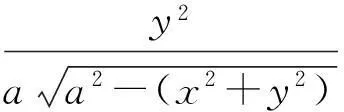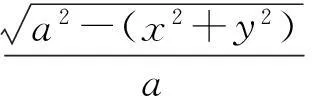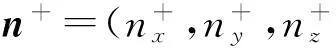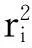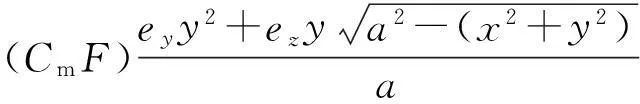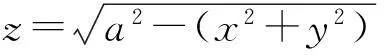激光辐照半球体碎片运动特性分析

激光辐照半球体碎片运动特性分析

金星，王大鹏，文明

(装备学院 激光推进及其应用国家重点实验室，北京 101416)

摘要激光辐照空间半球体碎片时，激光与碎片表面物质相互作用，使得碎片获得速度增量和角速度增量。基于激光辐照下反喷冲量计算模型，建立了不规则形状碎片平动/转动的速度增量/角速度增量的分析模型，对半球体碎片的激光辐照效应进行了分析，得到了速度增量和角速度增量的变化规律，为激光清除半球形空间碎片提供了分析依据和方法。

关键词空间碎片；激光辐照；半球体碎片；速度增量；角速度增量

作者简介金星(1962-)，男，朝鲜族，研究员，博士生导师，主要研究方向为激光航天应用技术。

中图分类号V520.7； V524.3

文章编号2095-3828(2015)06-0100-05

文献标志码A

DOI10.3783/j.issn.2095-3828.2015.06.022

AbstractAt the time of laser irradiation of hemispheroidal space debris, there is interaction between laser and the substance on the surface of the debris, so the debris obtains translation and angular velocity increment. Based on the reverse spraying impulse calculation model under laser irradiation, the paper establishes an analysis model for translation and rotational/angular speed increment of irregularly shaped debris. Based on the model, the paper conducts analysis on the effect of laser irradiation of hemispheroidal debris so as to conclude the rule of change of translation angular velocity increment and provide basis and method for analysis on removing hemispheroidal space debris using laser irradiation.

Keywordsspace debris; laser irradiation; hemisphere debris; translation velocity increment; angular velocity increment

Analysis on Motion Characteristics of

Hemispheroidal Debris Under Laser Irradiation

JIN Xing，WANG Dapeng，WEN Ming

(State Key Laboratory of Laser Propulsion & Application, Equipment Academy, Beijing 101416, China)

激光清除空间碎片方法被公认为是清除空间碎片的有效方法，得到了普遍的关注[1-3]，该方法最早由美国提出，国内也开展了相关研究[4-5]，目前都处于理论研究阶段。

激光清除空间碎片中，由于碎片几何形状不同，激光辐照下效应不同，对碎片的平动和转动的作用效果不同，因此，降低碎片飞行速度以便清除碎片的方法也不同。研究不但具有平动而且具有转动的空间碎片，对激光清除空间碎片具有重要意义，而目前国内外在该方面研究理论成果少有报道。

1激光辐照半球体碎片

如图1所示，激光辐照半球体空间碎片，由于半球体对称性，选取z轴为通过质心的半球体轴线，y轴在激光辐照方向与z轴确定平面内，建立右手坐标系，半球体底面为xy平面。

半球体半径为a，质心位置为(0,0,3a/8)，激光辐照方向单位矢量为e=(0,ey,ez)，激光辐照方向与xy平面的夹角为β(仰角表示，-π/2≤β≤π/2，)，dI为反喷冲量，dA为辐照面积，如图1所示，则有

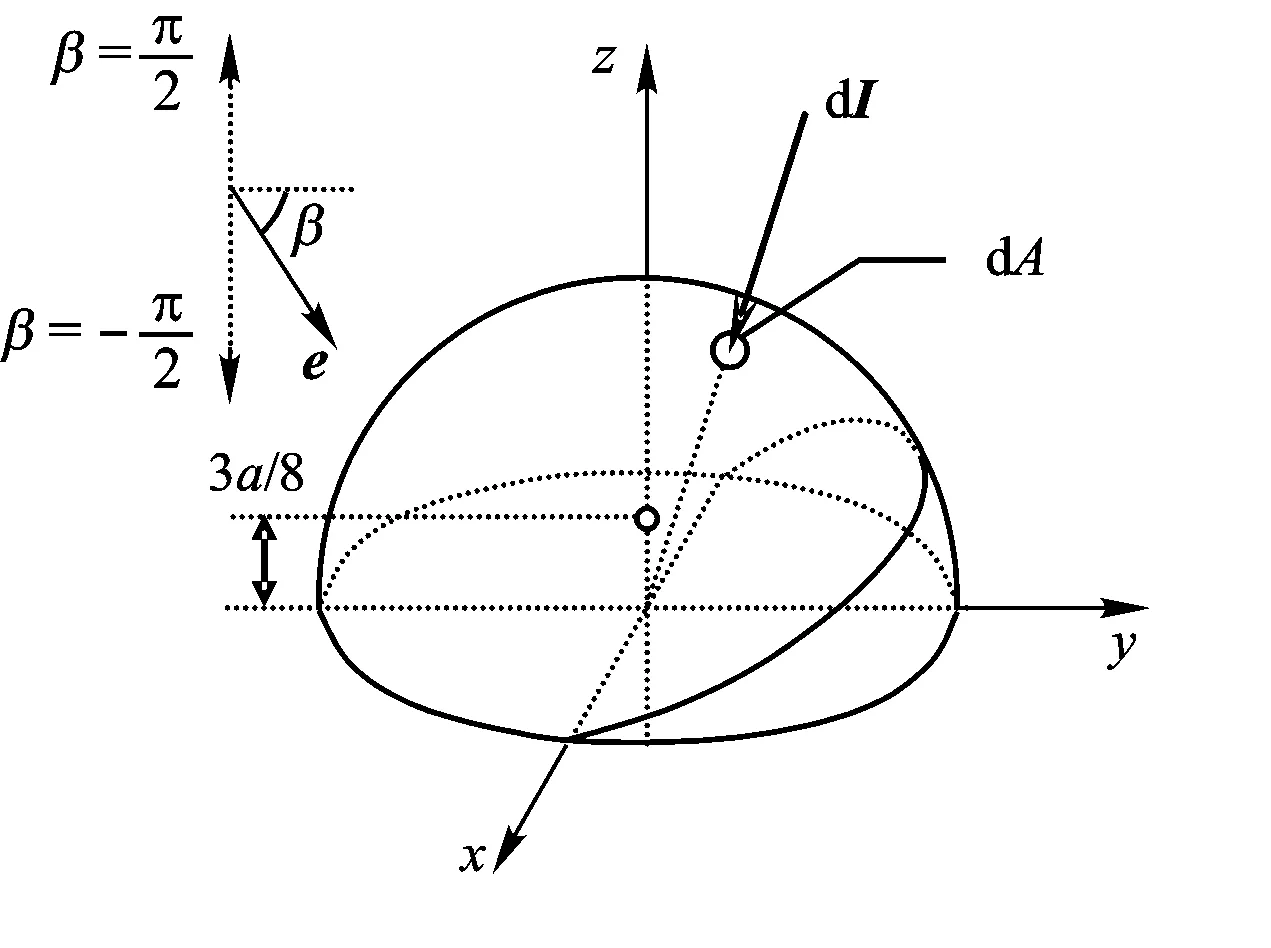
图1　激光辐照半球体碎片示意图

(1)

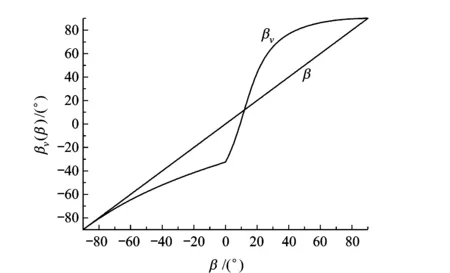
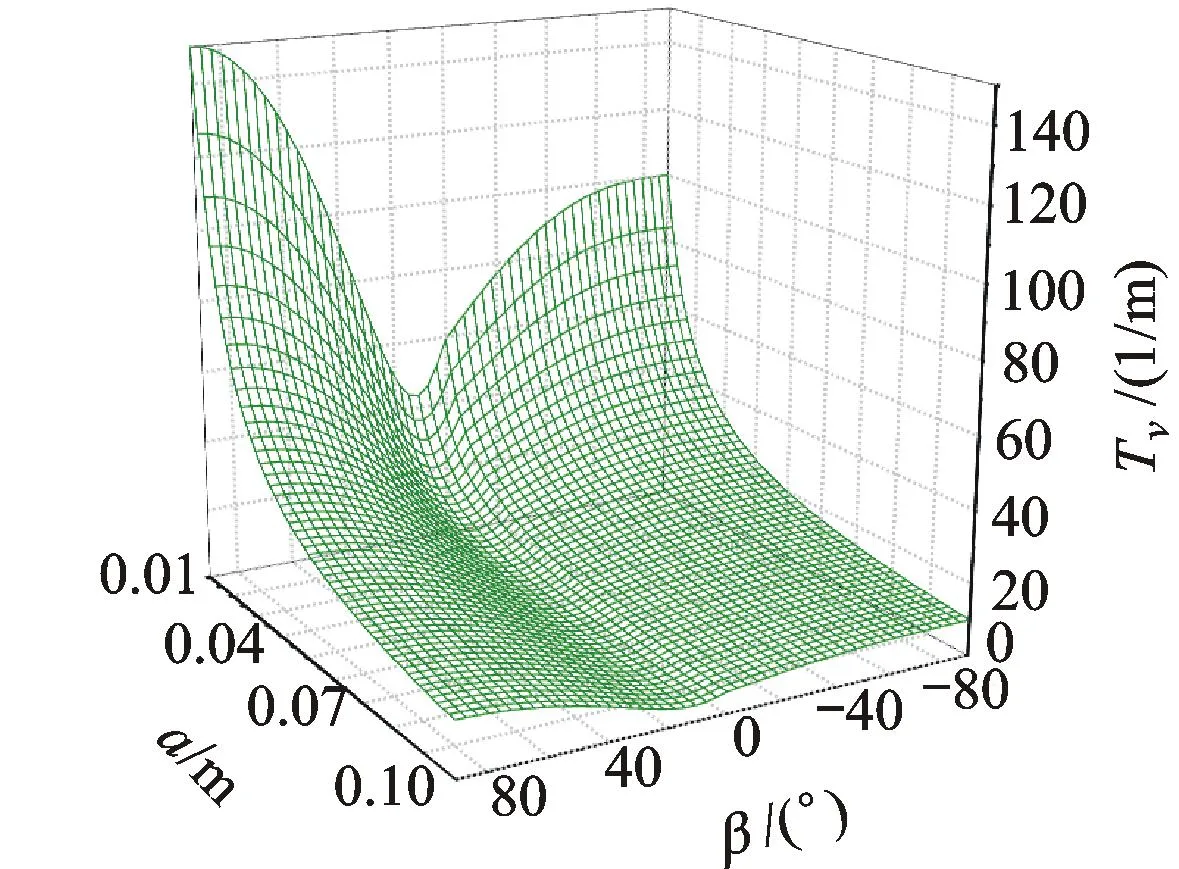
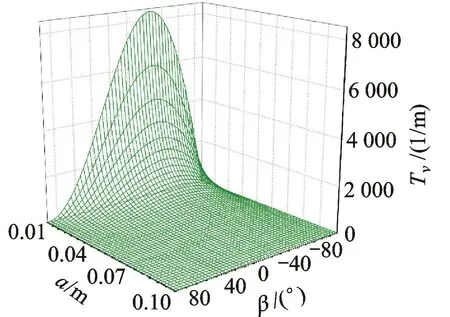
激光辐照半球体碎片方式，分为以下几种情况：(1) 当ez=1时，激光辐照底面；(2) 当0

2单脉冲冲量分析

在给定的Oxyz坐标系中，激光辐照方向单位矢量为e=(ex,ey,ez)，被辐照曲面的法向单位矢量为n=(nx,ny,nz)，则有

(2)式中，F为辐照产生作用力;Cm为冲量耦合系数。激光辐照任意曲面A上产生的单脉冲冲量为

(3)式中,积分是激光辐照曲面A上的曲面积分[6]69。

球体方程为

半球体被激光辐照部分的曲面为

由于

可得

其中

(4)

(5)

在xy平面中，被激光辐照区域投影曲线为外圆和内椭圆。外圆方程x2+y2=a2，为

内椭圆方程为

在曲面Σ+上Iy相应积分为

对上式进行积分运算得

可得

(6)

同理，曲面Σ+上Iz相应积分结果为

再加上底面πa2(0≤ez≤1)上Iz相应积分，可得

(7)

3速度增量分析

为方便计算和分析式(6)、式(7)，引入无量纲量表示与激光辐照方向相关部分：

(8)

(9)

则单脉冲冲量为

(10)

单脉冲速度增量与xy平面的夹角βv(仰角表示，-π/2≤βv≤π/2)为

(11)

即速度增量方向在激光辐照方向与碎片轴线确定平面内，偏离激光辐照方向的偏离角为

(12)

单脉冲速度增量大小为[6]69

式中,m为碎片质量。Δv表达式中，令

(13)

则有

(14)

式中,ρ为碎片密度。

4角速度增量分析

根据动量矩定理，单脉冲激光作用下，碎片以质心为中心的转动角速度增量为

(15)

式中,等式右边是反喷冲量dI相对质心(xC,yC,zC)的冲量矩；ΔωCi是以质心为中心对i轴(i=x,y,z)的角速度增量，对i轴转动惯量为

由于(dI)x=0，以及半球体的对称性可知ΔωCy=ΔωCz=0，只有ΔωCx不等于零，满足

其中

因此有

(16)

并且有

转动角速度增量为

(17)

令

(18)

根据式(17)、式(18),则有

(19)

满足ΔωCx/Δv=Tω/Tv。

5计算分析

图2所示为速度增量方向随着激光辐照方向的变化。经过计算，仅当β=-90°,β≈12°和β=90°时，有βv=β，即速度增量方向与激光辐照方向相同，否则速度增量方向与激光辐照方向偏离，但是速度增量方向总是在激光辐照方向与碎片轴线夹角之间。

图3为Tv(表征速度增量大小)随着激光辐照方向和碎片半径的变化，当β=-90°和β=90°时，速度增量取极大值；当β=0附近速度增量取极小值,并且随着碎片半径减小，速度增量增大。

图4为Tω(表征角速度增量大小)随着激光照方向和碎片半径变化，不同于图3中速度增量变化，当β=-90°和β=90°时，角速度增量为零；当β=0附近角速度增量取极大值，并且随着碎片半径减小，角速度增量增大，这是由于激光入射方向与半球体碎片结构特征共同引起的。

图2　速度增量方向与激光辐照方向变化

图3　T v随着激光辐照方向和碎片半径变化

图4　T ω随着激光辐照方向和碎片半径变化

6结论

基于激光辐照下反喷冲量计算模型，分析了半球体空间碎片的激光辐照效应，为激光清除不规则空间碎片提供了分析和设计方法，得出以下结论：

1) 半球体空间碎片在激光辐照下，既获得平动的速度增量，又获得转动的角速度增量，造成转动碎片轴线方向不断发生变化。

2) 半球体空间碎片的速度增量方向在激光辐照方向和碎片轴线所确定平面内，仅当激光辐照碎片底面或顶面或方向角约为12°条件下，速度增量方向与激光辐照方向相同,这是由于半球体特定结构的质心因素引起的结果；速度增量方向一般偏离激光辐照方向，但是速度增量方向在激光辐照方向和碎片轴线方向夹角之间。

3) 半球体空间碎片的角速度增量方向垂直激光辐照方向和碎片轴线所确定平面，当激光辐照方向角为零度时附近角速度增量取极大值。

参考文献(References)

[1]PHIPPS C R,ALBRECHT G,FRIEDMAN H,et al.ORION:clearing near-earth space debris using a 20-kw,530-nm,earth-based,repetitively pulsed laser[J].Laser and Particle Beams,1996,14(1):1-44.

[2]EARLY J T,BIBEAU C,PHIPPS C R.Space debris de-orbiting by vaporization impulse using short pulse laser[C]//Proceedings of SPIE.Sendai:SPIE，2004:441-452.

[3]KAPAN M H.Survey of space debris reduction methods[C]//AIAA SPACE 2009 Conference & Exposition.Sendai:AIAA,2009:1-11.

[4]金星,洪延姬,李修乾.cm级空间碎片的激光清除过程分析[J].强激光与粒子束,2012,24(2):281-284.

[5]金星,洪延姬,常浩.地基激光清除椭圆轨道空间碎片特性的计算分析[J].航空学报,2013,34(9):2064-2073.

[6]洪延姬,金星.激光清除空间碎片方法[M].北京:国防工业出版社,2013.

(编辑：李江涛)