急弯段闸孔出流的弯道水流特性研究

急弯段闸孔出流的弯道水流特性研究

郭红民1,2,覃闪1,蔡黎明1,曹光春1,张田甜1,胡文兵1

(1. 三峡大学 水利与环境学院，湖北宜昌443002； 2. 三峡地区地质灾害与生态环境湖北省协同创新中心,湖北宜昌443002)

摘要：在河弯处修建水工建筑物时，研究弯道水流特性对水工建筑物布置的影响十分重要。采用RNC κ-ε紊流模型对急弯段闸孔出流的弯道水流进行了三维数值模拟。通过模拟计算，比较分析了急弯段不同闸位、不同流量条件下闸孔过流时的流速分布、紊流动能、压强分布和环流等相关水流特性与变化规律。分析研究结果表明，闸坝位于弯道上游时，弯道对闸坝过流的影响最小，但需对闸坝下流弯道凸岸岸坡附近区域采取一定的防护措施；闸坝布置在弯道中游时，过闸水流受弯道的影响最小，闸室水流的稳定性、闸门的工作安全以及闸墩的空蚀破坏都是实际工程中需要注意的重点。数值模拟验证与物理模型试验结果吻合较好，计算精度较高，能够满足相关计算研究要求。

关键词：急弯段； 闸孔出流； 弯道水流； 水流特性； 数值模拟

中图分类号：TV135

文献标志码：A

文章编号：1009-640X(2015)03-0024-07

Abstract：Owing to the geologyical, topographical and hydrological factors, it is inevitable to build hydraulic structures in the river bend. So it is very important to carry out studies of influences given by the bendway flow on the layout of the hydraulic structures. The three dimensional numerical simulation of the bendway flow outflowing from the sluice orifices located on the rapid river bend has been made by using the RNC κ-ε turbulent model. With the aid of simulation calculation, a comparative analysis is made of the flow characteristics and variation law related to flow velocity distribution, turbulent kinetic energy and pressure distribution as well as circulation flow passing through the sluice under the conditions of different gate openings and different flow discharges. Analysis results show that as the dam sluice is located on the upper river bend, the influence given by the sluice on the flow passing through the dam sluice is the minimal, but some prevention measures should be taken for protecting the area close to the convex bank slope of the lower outlet bend against erosion; and the influence given by the river bend on the flow passing through the sluice is the maximal. Therefore, the stability of the flow flowing through the sluice chamber, the gate safety operation and the cavitation damage to the piers should be taken as the key points in consideration and to which more attention should be paid in practical engineering. The numerical simulation results, which are in good agreement with the results obtained from the physical model tests, can meet the requirements of the calculation studies.

DOI:10.16198/j.cnki.1009-640X.2015.03.005

收稿日期：2014-10-30

基金项目：国家自然科学基金资助项目(51178122)

作者简介：张丽娟(1969—)， 女， 辽宁辽阳人， 副教授， 主要从事软土工程性质、边坡工程， 桩基础等方面的教学与科研工作。E-mail: zhanglijuan1969@126.com

由于地质、地形和水文等因素的要求，水利枢纽工程有时不可避免要修建在河道弯道处，弯道水流是渠道和河道中很常见的一种水流运动现象，并且大多都是紊流流动。对弯道水流特性的研究，张红武等[1]在1984—1986年通过对4个河弯概化模型进行了水流运动规律的研究，得到了形式简单且适用天然河弯的环流流速垂线分布计算式；徐桂英[2-3]通过对闸前弯道建立物理模型进行了一系列的试验研究，得到了弯道水流流速分布和其他相关特性的规律；H. J. Vriend[4]对U型矩形弯道水流的各项特性作了详细的试验研究；刘曾美等[5]导出了弯道缓流的纵向和横向水面曲线计算式，提出了纵向水面线的简易计算方法；C. C. Fung 等[6]更是提出一种算法，可以自动识别矩形渠道内横向环流的存在和位置；赵小娥等[7]通过试验研究了在U形弯道上建闸后水流运动特性的变化。近年来，还有一些学者则通过数值模拟计算来作为理论和试验研究的补充，谭柱林等[8]有效预测了明渠180°弯道水流水面高度的变化影响范围及水面横比降的主要范围并分析了不同水深的平面流场和典型断面弯道环流分布；钟杰[9]研究了弯道上低水头拦河闸闸前的水流特性；R. D. Moser等[10-11]对小曲率低雷诺数弯曲河槽中的水流流动进行了直接数值模拟。对于强曲率的急弯河道，由于水流呈较强的三维特性，弯道环流发展充分，其在不同流量下对处于不同弯道位置的水工建筑物布置的影响，目前这方面研究尚不多见。本文利用Flow-3D软件，采用RNG 紊流模型，对急弯段闸孔出流的弯道水流进行了三维数值模拟，比较研究了急弯段不同闸位条件下闸孔过流时水流特性和变化规律，可为类似设计提供参考。

1数学模型

1.1控制方程

(1)

(2)

式中：ρ为体积分数平均的密度;μ为分子黏性系数；p为压强；μt为紊流黏性系数，μt=ρCμκ2/ε，其中Cμ为经验常数，Cμ=0.084 5; μ+μt为广义黏性系数；ui,uj分别为流速矢量在xi,xj方向的分量。

1.2紊流模型

RNGκ-ε模型是基于重整化群(Renormalization Group)的理论提出来的，经过了改进和实用化处理[12]，形式上类似于标准κ-ε模型，但在计算功能上强于标准κ-ε模型， RNGκ-ε模型考虑了旋转效应，因此也提高了强旋转流动计算精度，模型中包含了计算湍流Prandtl数的解析公式，并且对近壁区进行适当处理后可以计算低雷诺数效应。

(3)

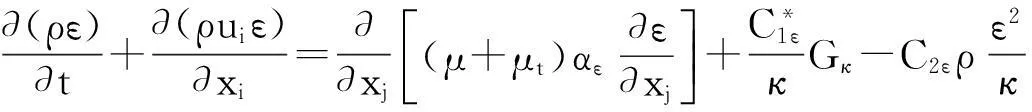
(4)

1.3数值方法和自由表面的确定

采用有限差分格式对上述控制方程组进行差分得到线性方程组，再采用广义极小残差算法(GMRES)对得到的线性方程组进行迭代求解。目前，大部分处理水气两相流的自由表面都是采用流体体积法(Volume of Fluid VOF)[13]，该方法往往会增加计算时间或使最终计算结果有较大偏差。本文对自由表面的描述采用TruVOF方法，该方法不考虑只含气体的控制单元，只计算含有液体单元，因此很大程度上减少了模型收敛所需的时间，对自由液面描述也更为准确。TruVOF法对流体界面的三维重构控制方程[14]为：

(5)

2几何模型和计算验证

2.1几何模型及网格划分

图1　弯道几何模型(单位： cm) Fig.1 A geometrical model for bend (unit： cm)

弯道几何模型构造分为水槽和闸坝两部分。弯道水槽底宽60 cm，边坡系数m为0.5，水槽底面坡度为0.005，水槽弯道转弯角度为90°，中心转弯半径为93 cm。闸坝轴线位置共布置3处，闸位1在弯道起点，闸位2在弯道转弯45°处，闸位3在弯道终点，闸坝皆为5孔平底闸孔，闸底板与水槽底等高，闸坝边墩上下游均以直立面与水槽边坡相接。验证流量1.1×107cm3/s，由于流量较小且验证试验闸门并未全开，验证模型的弯道水流形态为缓流，各验证断面留3个测压孔，用测压管测每个断面上凸、凹岸边和中心线水位，矩形堰测流量，光电流速仪测垂线纵向流速，采用五点法计算平均流速，测量误差0.01 cm。计算流量1为3.3×107cm3/s，计算流量2为5.5×107cm3/s，计算流量3为7.3×107cm3/s，计算流量下闸孔内的水流形态均为急流，相对缓流而言，闸孔内的水流更加不平衡，水流对闸坝的冲击和空蚀都会产生不可忽视的危害，且对下游水流流态也会有较大影响。模型布置如图1。

本文采用FAVOR法(Fractional Area/V￣o￣l￣u￣m￣e￣ Obstacle Representation)定义几何体和划分网格，采用多区块结构性网格(Multi-Block Grids)进行处理，通过连接式(Linked block)或者巢状式(Nested block)区块建立网格，有效解决传统单区块结构性网格为求模型细化而大量增加网格数量的问题。本文网格的划分采用两区块结构化网格，分别包含上游河道及闸坝和下游河道，通过连接式区块建立网格，网格为均一网格，网格尺寸1 cm。

上游进水口设置为流量边界条件，下游出口设定为自由出流，河道底部及左右侧壁均选择固壁边界；渠道顶部空气入口设定为对称边界，为零流动区域，且在边界上无需计算剪应力，在该边界上不会产生对流或者扩散通量。

2.2模型验证

验证计算选择前述验证流量和多个验证闸位进行，结果代表以如图1所示的验证闸位为例，闸孔开度e分别为1.5, 2.0, 2.5, 3.0, 3.5和4.0 cm。

2.2.1流速和主流线验证验证闸位、验证流量下流速和主流线验证计算结果见表1，可见，计算结果与模型试验基本吻合，误差均小于5%。

表1　断面流速和主流线偏离系数

2.2.2横比降和纵比降验证弯顶处的横比降与闸门相对开度之间的关系验证见图2。由图2可见，数值计算值和理论计算值符合文献[2]相关线性要求。闸孔开度e为3.5 cm时进行纵比降的验证(图3)，可见数值计算的结果与模型试验实测值基本一致。验证计算表明，所建立的三维数值计算模型能够满足相关计算研究要求，计算精度较高。

图2　最大横降比和闸门开度与水深比关系 Fig.2 Relationships between the maximum transverse gradient and the ratio of gate opening to depth

图3　闸门开度3.5 cm的弯道处水深 Fig.3 Depth at bend with gate opening 3.5 cm

3计算成果分析

3.1流速分布

不同计算流量下不同闸位的闸孔过流时的平面流速矢量分布云图见图4。闸位1时，弯道位于闸坝下游，闸孔进流及闸室过流受弯道水流的影响不大，进闸水流方向与闸墩基本平行，闸孔上游及闸室内、两侧的流速分布基本均匀对称，闸室内平均流速约130 cm/s；水流流出闸孔后受弯道影响，流速重新分布，凸岸流速变大，凹岸流速变小，其差值随流量增大而增大，最大流速比可达2.0～2.6。闸位2时，闸坝处于弯道正中，闸孔进出流均受弯道水流影响，各流量条件下，主流在进闸前与闸墩呈40°～45°的夹角；过闸水流在闸室内和出闸后的流速分布仍受弯道影响，闸室内平均流速约为闸位1时室内平均流速的90%，闸孔下游流速分布仍呈现凸岸大，凹岸小的情况，其流速比约为1.3～1.6。闸位3时，弯道位于闸坝上游，主流在进闸时与闸墩呈20°～25°夹角，较闸位2时主流与闸墩夹角有较大减小；水流在进入各闸孔时与闸墩夹角的规律为越靠近凹岸夹角越小，越靠近凸岸夹角越大，变化幅度约在5°～55°，闸室内平均流速约为闸位1时室内平均流速的80%；闸坝下游渠段虽已为直段，但流速分布仍受前段弯道的影响，呈现凹岸流速大，凸岸流速小的现象，其流速比值约为1.1~1.2。

图4　不同闸位的平面流速分布(单位：cm/s) Fig.4 Distribution of plane velocities (unit：cm/s)

3.2湍流动能分布

计算流量3时不同闸位的闸孔过流时的平面湍流动能分布见图5。对于同一闸位，不同流量时的湍流动能分布规律基本相同，各部位湍流动能随流量增大而增大。闸位1时，闸室内湍流动能分布均匀且对称，最大湍流动能约150～190 cm2/s2，闸坝出流下游的湍流动能核心区主要位于凸岸岸坡附近区域，该区域的湍流动能约580～690 cm2/s2。闸位2时，湍流动能核心区主要分布在闸室内的闸墩边墩附近和闸孔下游凸岸处，闸室内的最大湍流动能约为闸位1时闸室内最大湍流动能的1.9倍，闸坝下游凸岸区域的湍流动能为370～460 cm2/s2。闸位3时湍流动能核心区主要分布在闸孔下游，闸室内的最大湍流动能在闸室偏下游处，约为闸位1时闸室内最大湍流动能的1.1倍，而该闸位时闸孔下游的湍流动能明显小于闸位1和闸位2时，该区域范围的湍流动能为230～310 cm2/s2，是闸位1时核心区湍流动能的40%～50%，是闸位2时核心区湍流动能的60%～70%。

图5　不同闸位下平面湍流动能分布(单位：cm 2/s 2) Fig.5 Distribution of plane turbulent kinetic energy of flow 3 (unit: cm 2/s 2)

3.3压强分布

图6　不同闸位下平面压强分布(单位：Pa) Fig.6 Distribution of plane pressure of flow 3 (unit: Pa)

不同计算流量下不同闸位闸孔过流时的平面压强分布见图6。由图6可见，同一闸位不同流量时的压强分布规律基本相同，最大正压均出现在闸墩头部。闸位1时闸孔上游和闸室内压强基本均匀对称，未出现负压，最大正压约为1.94 kPa。闸位2时压强分布规律为闸孔附近凹岸压强总体上大于凸岸，凹岸平均压强约为凸岸平均压强的1.6倍，最大正压约1.97 kPa，流量2和流量3在凸岸边墩下游处出现负压，其最大负压约-0.59 kPa。闸位3时最大正压约1.97 kPa，各计算流量下凹岸边墩下游处均出现负压，最大负压约-0.20 kPa。

3.4横向环流

流量3闸位3前径向横断面的横向环流见图7。闸位1时由于闸坝位于弯道上游，其流速分布基本不受弯道影响，其闸前未出现横向环流，局部横向流速主要受到边墩收缩河道影响而指向河道中心线。闸位2由于处于弯道正中，闸坝在过流时受弯道影响较大，闸前的横断面出现逆时针(上游向下游视角，下同)横向环流，环流中心位置偏向凹岸。闸位3时闸坝虽已处于弯道尾端，但流速分布仍受前段弯道影响，闸前横断面仍出现逆时针横向环流，环流中心位置也偏向凹岸。

图7　不同闸位横向环流变化 Fig.7 Changes of transverse circulation

4结语

本文采用RNGκ-ε紊流模型，对急弯段闸孔出流的弯道水流进行了三维数值模拟，数值模拟验证与物理模型试验结果吻合较好，计算精度较高，能够满足相关计算研究要求。通过模拟计算，比较分析了不同流量下不同闸位时闸坝过流的部分水力学特征和规律，结果表明：

(1)闸坝位于弯道上游时，进闸水流方向与闸墩基本平行，闸室内的流速均匀对称，闸室内的湍流动能较小，且闸前未产生横向环流，闸墩附近没有出现负压，但是闸坝出流下游弯道凸岸岸坡附近区域的湍流动能较大，约为闸位2的1.5～1.6倍，闸位3的2.2～2.5倍，实际工程设计中需对该岸坡采取一定的防护措施。

(2)闸坝在弯道中间时，过闸水流受到弯道的影响较大，闸前有明显横向环流，水流在进闸时与闸墩呈较大夹角约为40°～45°，对闸墩的横向冲击较大，同时该闸位相对另外两种闸位，闸室内湍流动能也最大，约为闸位2的1.9倍，闸位3的1.8倍，不利于闸室水流稳定和闸门安全工作；该闸位闸墩下游处还会出现较大负压，可能对闸墩产生空蚀破坏；闸坝下游凸岸岸坡附近区域也出现了较大的湍流动能，该处岸坡稳定也需注意。

(3)闸坝在弯道尾端时，闸前也出现了较为明显的逆时针横向环流，水流在进闸时仍与闸墩呈一定夹角，但较闸位2有所减小；该闸位部分闸墩下游也出现了负压，同样需要防止空蚀破坏。该位置闸坝下游出流相对平稳，湍流动能值较小，对岸坡影响较小。

参考文献：

[1]张红武, 吕昕. 弯道水力学[M]. 北京： 水利电力出版社, 1993. (ZHANG Hong-wu, LV Xi. Hydraulics of curved flow[M]. Beijing: Water Power Press, 1993.(in Chinese))

[2]徐桂英. 闸前弯道水流特性的试验研究[J]. 武汉水利电力大学学报, 1995, 28(3): 338- 341. (XU Gui-ying. Experimental study on the behavior of flow through the curved channel in front of a sluice gate[J]. Journal of Wuhan University of Hydraulic and Electric Engineering, 1995, 28(3): 338- 341. (in Chinese))

[3]徐桂英. 闸前梯形断面90°弯道水流垂线纵向流速分布的实验研究[J]. 中国农村水利水电, 1997(1)： 42- 43. (XU Gui-ying. Experimental study on the 90° curved flow of vertical longitudinal velocity at trapezoid section before the gate[J]. China Rural Water and Hydropower, 1997(1): 42- 43. (in Chinese))

[4]VRIEND H J. Flow measurements in cured rectangular channel: Part 2. Rough bottom[R]. The Netherlands: University of Delft, 1981: 5- 81.

[5]刘曾美, 吴俊校, 黄国如. 河渠弯道缓流水面曲线计算探讨[J]. 水利水运工程学报, 2008(2): 54- 59. (LIU Zeng-mei, WU Jun-xiao, HUANG Guo-ru. Computation of water surface curve of suberitical flow in meandering river channel[J]. Hydro-Science and Engineering, 2008(2): 54- 59. (in Chinese))

[6]FUNG C C, CHUNG K P, CHANDRATILLEKE T. Dentification of secondary flow pattern in a heated curve rectangular channel using image processing technique[C]∥IEEE Instrumentation and Measurement Technology Conference, Institute of Electrical and Electronics Engineers Inc, 2001: 2093- 2098.

[7]赵小娥, 钟杰, 刘兴年, 等. U形弯道建闸对水流运动特性的影响试验[J]. 水利水电科技进展, 2010, 30(3): 47- 49, 57. (ZHAO Xiao-e, ZHONG Jie, LIU Xing-nian, et al. Experimental study on influences of sluice construction in a U-shape bend on characteristics of flow motion[J]. Advances in Science and Technology of Water Resources, 2010, 30(3): 47- 49, 57. (in Chinese))

[8]谭柱林, 彭杨. 明渠弯道水流三维数值模拟[J]. 水运工程, 2012(3): 46- 49. (TAN Zhu-lin, PENG Yang. Three-dimensional numerical simulation of bend flow in open channel[J]. Port & Waterway Engineering, 2012(3): 46- 49. (in Chinese))

[9]钟杰. 弯道低水头拦河闸闸孔分流比试验研究[J]. 长江科学院院报, 2011, 28(3): 28- 32. (ZHONG Jie. Experinental study on flow diversion ratio of low head sluice built in curved channel[J]. Journal of Yangtze River Scientific Research Institute, 2011, 28(3): 28- 32. (in Chinese))

[10]MOSER R D, MOIN P. Direct numerical simulation of curved turbulent channel flow[R]. CA: NASA Ames Research Center, 1984.

[11]MOSER R D, MOIN P. The effects of curvature in wall-bounded turbulent flow[J]. Journal of Fluid Mechanics, 1987, 175: 479- 510.

[12]RIJN L C.Sediment transport, Part I: bed load transport[J]. Journal of Hydraulic Engineering, 1984, 110(10): 1431- 1456.

[13]HIR C W, NICHOILS B D. Volume of fluid(VOF) for the dynamics of free boundaries[J]. Journal of Computational Physics， 1981, 39(1): 201- 225.

[14]MATTHEWS B W, FLETCHER C A J, PARTRIDGE A C, et al. Computations of curved free surface water flow on spiral concentrators[J]. Canadian Metallurgical Quarterly, 1999, 125(11): 1126- 1139.

A study of bendway flow characteristics outflowing from sluice orifice on rapid river bend

GUO Hong-min1,2, QIN Shan1, CAI Li-ming1, CAO Guang-chun1, ZHANG Tian-tian1, HU Wen-bing1

(1.CollegeofHydraulicandEnvironmentalEngineering,ChinaThreeGorgesUniversity,Yichang443002,China; 2.CollaborativeInnovationCenterforGeo-HazardsandEco-EnvironmentinThreeGorgesArea,Yichang443002,China)

Key words： rapid river bend; outflow from sluice orifice; bendway flow; flow characteristics; numerical simulation

张丽娟， 刘仁钊. 南沙港淤泥固化前后物理力学性能和微观结构变化[J]. 水利水运工程学报, 2015(3): 31-36. (ZHANG Li-juan, LIU Ren-zhao. Physico-mechanical properties and changes in microstructure of silt before and after solidification in Nansha port[J]. Hydro-Science and Engineering, 2015(3): 31-36.)