软黏土不排水循环应力应变关系的数值模拟

软黏土不排水循环应力应变关系的数值模拟

王哲学1, 2,王建华1, 2,程星磊1, 2

(1. 天津大学水利工程仿真与安全国家重点实验室, 天津300072； 2. 天津大学 岩土工程研究所，天津300072)

摘要：对程星磊等提出的总应力形式增量弹塑性本构模型进行二次开发，以模拟复杂应力状态下软黏土的响应。通过Newton-Raphson算法，对材料非线性问题进行迭代求解；针对本构模型中应力反向等一系列关键性问题，应用欧拉切线算法编写了有限元程序，并结合子增量方法提高了计算精度。预测了软黏土在轴对称应力状态下的响应，得到了应力应变关系曲线，将其与单元预测结果进行比较，二者趋于一致，从而验证了有限元程序编写的合理性。利用该程序模拟三轴不固结不排水试验，模拟结果与试验吻合良好，表明该本构模型有限元程序可以反映轴对称应力状态下软黏土的不排水应力应变特性，可应用于更加复杂边值问题的模拟计算。

关键词：循环荷载； 饱和软黏土； 应力应变； 本构模型； 欧拉切线算法； 三轴试验

中图分类号：TU43

文献标志码：A

文章编号：1009-640X(2015)03-0081-07

Abstract：An incremental elasto-plastic constitutive model in the form of total stress developed by CHENG Xing-lei et al can effectively reflect the undrained cyclic stress-strain response of the saturated soft clay. In order to simulate the response of the soft clay under complex stress states，a secondary development for the constitutive model is conducted by use of the finite element method. The Newton-Raphson method is applied to solve iteratively the material nonlinear problem; considering a series of key problems such as stress reversing, in programming the model, Euler tangent algorithm is adopted，with a sub-incremental method improving calculation accuracy. The response of the soft clay under axisymmetric stress states is predicted, and the stress-strain relationship curves are received, which is compared with the results given by the unit predicting. The analysis comparison results show that it is in good agreement, verifying the rationality of the finite element program. The finite element program is applied to simulate unconsolidated undrained triaxial tests， and the results are in good agreement with the experiments, which indicates that the finite element program of the constitutive model can describe the undrained stress-strain behavior of the soft clay under triaxial stress states. Furthermore, it can be applied to solve more complex boundary value problems.

DOI:10.16198/j.cnki.1009-640X.2015.03.013

收稿日期：2014-09-05

基金项目：江苏省水利科技项目(2013057)

作者简介：丁军(1967—)， 男, 江苏泰兴人, 高级工程师, 主要从事水泵、水闸设计与研究工作。

嵌固在海洋软黏土中的锚固基础在风、浪等荷载作用下，为维持上部结构工作性能，必须保持自身稳定，因此需要合理分析软黏土中锚固基础在循环荷载作用下的变形失稳过程。锚固基础的变形不仅与基础本身有关，海洋中软土地基对其影响更为重要。因此研究循环荷载下软黏土的不固结不排水应力应变关系具有重要意义。J. H. Prévost[1-2]提出了基于运动硬化塑性理论的多面模型，但模型的变形分析很复杂，需要记忆所有假设的多个次加载面形状，并分析它们的移动，导致在数值应用中计算过程复杂。Y. F. Dafalias等[3-4]建立了包括1个正常屈服面和1个次加载面的两面模型，大大简化了多面模型；后来他们又将两面模型中的次加载面简化为一点，提出了单面模型[5]。两面和单面模型都叫边界面模型[6-8]。由于改进初期的边界面模型映射中心固定在原点，无法合理描述土单元的应力应变滞回曲线[9]，且硬化模量场的演化过程表述较为复杂，不便于应用到数值分析中。程星磊等[10]采用总应力形式在偏应力空间中构建硬化模量场，硬化模量插值函数数学表达简洁，引入模型参数较少，硬化模量场的演化规律表述简单，跟踪循环应力路径所需记忆的参数较少，便于计算应用。通过上述分析，针对程星磊等建立的软黏土循环弹塑性本构模型进行二次开发，并对循环三轴试验进行数值模拟，通过计算结果与试验结果的比较，验证该本构模型数值分析方法的可行性。

1本构模型简述

采用Mises屈服准则构建边界面约束方程：

(1)

依据经典弹塑性理论[11]，有总偏应变增量计算式：

(2)

式中：deij为总偏应变增量；G为弹性剪切模量；H′为塑性硬化模量；dskl为当前应力点的偏应力增量。

引入弹塑性硬化模量H，令：

(3)

在初始加载或应力反向时，塑性变形模量为无穷大：

(4)

图1　弹塑性模量的映射规则图解 Fig.1 Elasto-plastic mapping rule for loading and unloading

(5)

式中：Hmax为弹塑性模量最大值，取2G；μ为反映剪应变累积速率和大小的模型参数。

在不固结不排水条件下，边界面半径A0和弹性模量G可通过不固结不排水循环三轴试验得到。在三轴应力状态下，式(1)简化为下式：

(6)

式中：σz为试样轴向应力；σr为试样径向应力。

由于初始应力应变响应均遵循同一初始加荷曲线，且可用式(7)拟合，则拟合曲线的渐近线所对应的强度就是边界面半径A0，其值等于1/b；曲线的初始切线模量记为E，其值等于1/a。另外，弹性剪切模量G可由式(8)求得：

(7)

(8)

式中：a和b为拟合函数中的待定系数；ν为泊松比，不排水时取0.5。

参数μ可以用下式表示：

(9)

式中：μ0为反映累积偏应变大小的待定系数；dγ8p为八面体累积剪应变增量，以此描述偏应变累积变化的速率和趋势。对试验数据采用式(10)拟合：

(10)

式中：c，d为待定系数；N为循环次数。则有dγ8p=cdNd-1

(11)

下面结合某一具体三轴试验，给出待定系数c，d，μ0的确定方法。图2给出了该三轴试验得到的静应力比τ8,a/τ8,f=0.3和0.5时八面体累积剪应变随振次的变化关系。 用式(10)拟合试验数据，如图中虚线所示，得到不同静应力比τ8,a/τ8,f，不同循环应力比τ8,cy/τ8, f下的待定系数c和d值。通过式(11)可得应力循环一周八面体累积剪应变增量dγ8p。

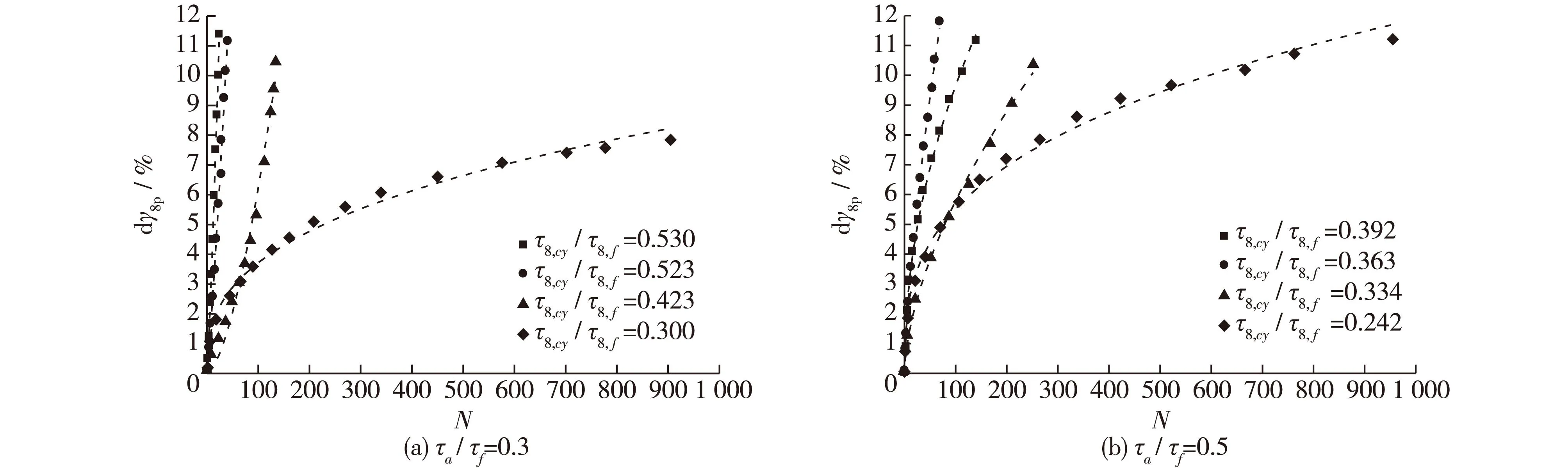
图2　三轴压缩时八面体累积剪应变随循环次数的变化关系曲线 Fig.2 Relation curves of octahedral cumulative shearing strain and cycle times in triaxial compression

进一步，可通过试算方法确定μ0，即利用式(9)将dγ8p代入式(5)，给定一个μ0，通过式(2)计算得到破坏振次下的八面体累积剪应变。这里规定按照静偏应力作用下试样的八面体静剪应变与静偏应力与循环应力共同作用下八面体循环累积剪应变之和达到14%的标准确定循环破坏次数。若模型计算所得破坏振次下的八面体累积剪应变与试验结果一致，那么此时的μ0值即为该试验应力条件下待定系数μ0的取值。

这样，不同静应力比τ8,a/τ8,f，不同循环应力比τ8,cy/τ8,f下的参数c，d，μ0都已给出(见表1)。则对任意循环应力比下的参数值，可通过线性插值方法确定。

表1　不同静应力比、循环应力比下拟合函数中的待定系数c，d及μ 0取值

至此，软黏土不固结不排水条件下循环本构关系及模型参数的确定方法已完全给出。

2本构模型二次开发

2.1平衡迭代过程

图3　增量内迭代过程 Fig.3 Iterative process in increment

非线性平衡方程采用Newton-Raphson迭代算法[12]求解。在迭代过程中，把整个加载过程分成若干分段，荷载以增量形式施加在结构上，在增量内部进行若干迭代，直至达到所需精度为止。整个流程融合了增量与迭代的过程[13]。在增量内的迭代过程(见图3)作如下说明[14]：①根据当前的应力状态nσ ，确定弹塑性矩阵Dep，进而确定刚度矩阵K 。②由Δu=K-1ΔR ，得到位移增量。其中，ΔR 为外加荷载增量，Δu 为位移增量。③由Δε=BΔu ，得到应变增量。④采用应力更新算法，通过当前应力状态以及上一步得到的应变增量计算应力增量Δσ，进而得到新的应力状态n+1σ。⑤判断内力、外力是否平衡，位移是否满足收敛标准：若不满足，返回①，继续进行迭代；若满足，进入下一增量计算。

2.2应力更新算法

对第④步的应力更新算法做出详细阐述，由应力应变关系式(2)，可得：

(12)

由上述关系式可得到偏应力增量。静水压力增量可由弹性虎克定律得到：dσm=3Kdεm

(13)

由此得到应力增量大小： dσij=dσmδij+dsij

(14)

将式(8)和(9)代入式(10)，有：

(15)

得到增量形式的弹塑性应力应变关系，整理成矩阵形式：dσ=Depdε

(16)

式中：dσ为应力张量；dε为应变张量；Dep为弹塑性矩阵，由于在应力应变关系曲线上Dep为切线方向，因此也叫切线矩阵。

因此，本构关系的积分式为:Δσ=∫Depdε

随着机动车保有量的迅猛增长，人们就医出行选择开私家车前往医院的现象越来越普遍，大大增加了医院周边交通流。随着生活水平的改善，人们对于更好的医疗服务需求显得更加重视，大型医院有着更好的医疗硬件设施和专家门诊服务，所以前往大型医院看病的人员越来越多。在这样的背景之下，涌向大型医院的人流与车流已经远远超出了医院设计之初的承载能力，而医院只是对建筑进行扩建来增加医院的就医能力，医院容量的扩大则会带来更大的交通需求，一味地对医院进行扩建不但不能从根本上解决问题，反而会增加医院周边的交通流，导致供需失衡越来越严重。

(17)

在计算过程中，采用式(16)将式(17)线性化。但是这种计算方法必然带来偏差[15]。可采取减小增量大小的方法减小这种偏差。

当应力状态趋于边界面附近时，由式(5)得硬化模量趋于零，由式(17)得偏应力增量趋于零，因此应力状态点将始终保持在边界面以内。但实际计算中，由于采用式(16)所示的欧拉切线方法对式(17)进行线性化，而欧拉方法只有在偏应变增量趋于无限小的时候才能足够准确，因此在边界面附近时，应力增量dσij有可能大于零，从而使应力状态超出边界面。但边界面是破坏面，土体的应力状态不允许超过边界面。这将导致计算出错。采用子增量方法虽然大大减小了偏应变增量的大小，但是也不足以保证应力状态不超过边界面。为此，将超出边界面的点沿边界面的半径方向径向拉回至边界面，并认为这一点的应力状态即为当前的应力状态。具体做法是，计算应力空间原点与当前应力点之间距离，按照边界面半径与该距离比例对当前应力点各个应力分量进行线性缩放，则缩放后的应力点必然落在边界面上。进一步利用修正后的应力状态建立与之相适应的弹塑性矩阵Dep。这样就保证了任意时刻的应力状态只能在边界面以内或者在边界面之上；而到达边界面的点在持续加载的条件下，应力状态始终保持在边界面上，类似于理想弹塑性模型中的塑性加载状态。与之相适应的弹塑性矩阵，则保证了应力与应变状态的一致性，有利于后续分析的收敛。

(18)

图4　有限元预测结果与单元预测结果比较 Fig.4 Comparison between FEM results and unit predicted results

如果这一余弦值为正或零，说明应力增量张量与当前边界面外法线张量呈锐角或直角，则此时没有应力状态改变；如果这一余弦值为负，说明应力增量张量与当前边界面外法线张量呈钝角，则认为此时应力状态发生改变。三轴应力状态只有夹角为0°(应力状态不变)和180°(应力状态反向)两种应力状态的改变形式。

3有限元程序验证

把有限元程序和单元预测循环三轴不固结不排水试验得到的应力应变曲线进行对比(图4)。实线为有限元计算结果，虚线为单元预测结果。围压为100 kPa，静强度大小为τ8,f=16 kPa，静剪应力比τ8,a/τ8,f=0.5，循环剪应力比τ8,a/τ8,f=0.392，其他参数为：A0=31 kPa,G=745.76 kPa,c=0.861,d=0.606,μ0=8。

图4表明数值算法结果与基于此本构模型进行的单元预测结果吻合良好，说明数值算法程序能够正确反映本构模型的应力应变关系，此程序编写是合理的。

4三轴试验模拟

表2　三轴试验模型参数

针对前文所述三轴试验，静应力比τ8,a/τ8,f=0.5的三轴压缩试验和三轴拉伸试验分别进行数值计算。根据表1，通过插值的方法确定模型所采用的参数(表2)。

将循环八面体累积剪应变随循环次数的变化关系进行比较(图5)。对于图5(a)中τcy/τf=0.334的试验模拟，当循环应变大于10%时，计算得到的曲线与试验曲线略有差异，但循环累积应变小于10%时，二者吻合良好。如上所述，当静应变与循环累积应变之和达到14%时，即视为土体破坏。这里静应变约为4%，因此循环累积应变达到10%时，试样已经破坏，即在土样破坏之前可以较好地模拟试验结果。图5(b)中τcy/τf=0.180的试验模拟，循环次数达900次，模拟结果与试验有较好的一致性，且曲线趋于平稳，因此该模型可以描述循环次数较大时土体的应力应变响应。综上，相同振次下的累积变形预测结果与试验结果较为一致，此本构模型的有限元程序可以较好地反应循环变形的累积特性。

图5　循环累积剪应变随振次的变化 Fig.5 Cyclic cumulative shear strain vs. the number of cycles

将静剪应力比τ8,a/τ8,f=0.5、循环剪应力比τ8,cy/τ8,f=0.392的应力应变曲线进行比较(图6)。结果表明，模型可较好地描述循环加载时应力应变曲线的滞回特性及应变累积特性。

图6　三轴应力-应变曲线 Fig.6 Triaxial stress-strain curves

上述分析表明，该本构模型有限元程序可以描述循环三轴应力状态下软黏土的应力应变关系，可进一步推广至更加复杂的应力状态。

5结语

(1)在数值实现过程中，采用Euler切线方法对本构关系积分进行线性化，并采用子增量法提高了计算精度，加快了后续迭代的收敛速度。

(2)由于欧拉方法不可避免会使应力状态超出边界面，因此采用径向返回的方法将其拉至边界面上，以保证任何单元的应力状态均不会超出具有破坏意义的边界面。

(3)在偏应力空间中，采用应力增量与像应力点在边界面上外法线方向的夹角判断应力状态改变，确定加载卸载状态。

(4)通过有限元方法进行二次开发，成功地将此本构模型应用到了数值计算中，对三轴压缩和拉伸试验进行预测，结果证明此本构模型数值实现方法合理。对于更复杂的应力状态还有待于进一步研究。

参考文献：

[1]PRÉVOST J H. Mathematical modelling of monotonic and cyclic undrained clay behaviour[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1977, 1(2): 195- 216.

[2]PRÉVOST J H. Anisotropic undrained stress-strain behavior of clays[J]. Journal of the Geotechnical Engineering Division, ASCE, 1978, 104(GT8): 1075- 1090.

[3]DAFALIAS Y F, POPOV E P. A model of nonlinearly hardening materials for complex loading[J]. Acta Mechanica, 1975, 21(3): 173- 192.

[4]DAFALIAS Y F, HEMNANN L R. A boundary surface soil plasticity model[C]∥ Proceedings of International Symposium on Soils under Cyclic Transient Load. Rotterdam: Balkema Publ, 1980: 335- 356.

[5]DAFALIAS Y F, POPOV E P. Cyclic loading for materials with a vanishing elastic domain[J].Nuclear Engineering and Design, 1977, 41(2): 293- 302.

[6]DAFALIAS Y F. Bounding surface plasticity Part I: Mathematical foundation and hypoplasticity[J]. Journal of Engineering Mechanics, 1986, 112(9):966- 987.

[7]DAFALIAS Y F, HERRMANN L R. Bounding surface plasticity. Part II: Application to isotropic cohesive soils[J]. Journal of Engineering Mechanics, 1986, 112(12): 1263- 1291.

[8]ANANDARAJAH A , DAFALIAS Y F. Bounding surface plasticity. Part III: Application to isotropic cohesive soils[J]. Journal of Engineering Mechanics, 1986, 112(12): 1292- 1318.

[9]花丽坤，孔亮. 几种循环塑性模型的剖析和比较研究[J]．宁夏工程技术， 2003, 2(1)：19- 23. (HUA Li-kun, KONG Liang. Analysis and comparison of several cyclic plastic models[J]．Ningxia Engineering Technology, 2003, 2(1): 19- 23.(in Chinese))

[10]程星磊，王建华，李书兆. 软黏土不排水循环应力应变响应的弹塑性模拟[J].岩土工程学报，2014, 36(5): 933- 941. (CHENG Xing-lei, WANG Jian-hua, LI Shu-zhao. Elastoplastic simulation for undrained cyclic stress-strain response of soft clay[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(5): 933- 941. (in Chinese))

[11]张学言，闫澍旺. 岩土塑性力学基础[M]. 天津：天津大学出版社，2003: 88- 115. (ZHANG Xue-yan，YAN Shu-wang. Fundamentals of geotechnics plasticity[M]. Tianjin: Tianjin University Press, 2003: 88- 115. (in Chinese))

[12]王军祥，姜谙男. 完全隐式返回映射算法对岩土地基问题的求解[J]．工程力学，2013, 36(8): 83- 89. (WANG Jun-xiang, JIANG An-nan. Fully implicit return mapping algrithm for solving the problems of geotechnical foundation[J]. Engineering Machanics, 2013, 36(8): 83- 89. (in Chinese))

[13]朱伯芳. 有限单元法原理与应用[M]. 北京:中国水利水电出版社, 1998: 292- 302. (ZHU Bo-fang. The finite element method theory and applications[M]. Beijing: China WaterPower Press, 1998: 292- 302. (in Chinese))

[14]王勖成，邵敏. 有限单元法基本原理和数值方法[M]. 北京：清华大学出版社，1997: 510- 511.(WANG Xu-cheng, SHAO Min. The basic principles of the finite element method and numerical methods[M]. Beijing: Tsinghua University Press, 1997: 510- 511. (in Chinese))

[15]HU Cun, LIU Hai-xiao. Implicit and explicit integration schemes in the anisotropic bounding surface plasticity model for cyclic behaviours of saturated clay[J]．Computers and Geotechnics, 2014, 55: 27- 41.

Numerical simulation of undrained cyclic stress-strain response of soft clay

WANG Zhe-xue1,2, WANG Jian-hua1,2, CHENG Xing-lei1,2

(1.StateKeyLaboratoryofHydraulicEngineeringSimulationandSafety,TianjinUniversity,Tianjin300072,China； 2.GeotechnicalEngineeringInstitute,TianjinUniversity,Tianjin300072,China)

Key words： cyclic load; saturated soft clay; stress-strain curve; a constitutive model; Euler tangent algorithm; triaxial tests

丁军， 丁庆朋. 胥浦活水泵站肘形进水流道流态分析及优化[J]. 水利水运工程学报, 2015(3): 88-94. (DING Jun, DING Qing-peng. Flow pattern analysis and optimization of elbow inlet conduits of Xupu running water pumping station[J]. Hydro-Science and Engineering, 2015(3): 88-94.)

E-mail：djdj1031@163.com