黑箱函数优化问题中的响应面优化方法

黑箱函数优化问题中的响应面优化方法*

齐静

(重庆师范大学 数学学院，重庆 401331))

摘要：在实际科研领域和工程应用中经常会遇到一类问题，就是高价黑箱函数问题，针对高价黑箱函数的全局最优化问题，开展了径向基函数和响应面相结合的研究;针对径向基函数中响应面模型及目标值的选取进行了理论分析；提出了一种新的选取策略，不同的选取策略必然会导致不同的搜索模式，从而影响优化效果。

关键词：高价黑箱函数；全局优化；径向基函数；响应面模型；对称拉丁超立方设计

doi:10.16055/j.issn.1672-058X.2015.0012.006

收稿日期：2015-05-15；修回日期：2015-06-18.

基金项目：*国家自然科学基金(10871217).

作者简介：齐静(1990-)，女，河南南阳人，硕士研究生，从事全局最优化方法研究.

中图分类号：O241.3文献标志码：A

在实际科研领域和工业应用中，经常会遇到一类问题，这类问题的函数值计算代价高昂，计算一次函数值就需要几个小时甚至更长的时间，而且这类函数通常没有显式表达式，导数也不可用，称这一类问题为高价黑箱函数(Expensive Black Box Function)[1]。将采用函数逼近的方法来解决其全局最优化问题。径向基函数插值是处理散乱数据的一种新的有效的方法，它具有计算格式简单、计算工作量小[2]等特点。近年来，国内外的一些学者对高价黑箱函数的优化问题进行了一系列的研究，研究表明：径向基函数插值是解决高价黑箱函数优化问题的一种新的有效的方法。

1高价黑箱优化问题

高价黑箱函数的全局最优化问题[1]为

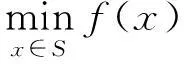
(1)

如果存在一个点x*∈S使得对任意的x∈S都有不等式f(x*)≤f(x)成立，就称x*是问题(1)的全局最优解，f(x*)称为f(x)在S上的全局最优值;如果存在x′∈S，在x′的一个δ邻域B(x′,δ)内，对任意的x∈S∩B(x′,δ)内都有不等式f(x′)≤f(x)成立，就称x′是问题(1)的一个局部最优解，f(x′)称为f(x)在S上的局部最优值。

1.1径向基函数插值模型

给定n个不同的点x1,x2,…,xn∈Rd，并且它们的函数值f(x1),f(x2),…,f(xn)也是已知的，取定径向函数φ，寻找具有如下形式的函数:

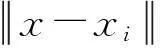
1.2径向基函数插值的基本思想[3]

(1) 生成初始点，对初始点进行函数值计算；

(2) 选定径向基函数，构造径向基函数插值模型；

(4) 求解下一个迭代点xn+1，并对xn+1进行函数计算；

(5) 使用新的数据点更新径向基函数插值模型；

(6) 重复(3)-(5)，直到收敛。

1.3SLHD方法选取初始点

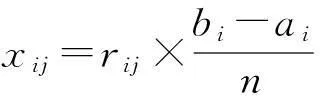
1.4响应面模型的构建

根据已选好的初始点x1,x2,…,xn及其函数值f(x1),f(x2)，…,f(xn)，构建响应面模型，但是发现f(x1),f(x2)，…,f(xn)中，有些函数值可能非常小而有些函数值就可能非常大，这些极端的函数值会对响应面的构建造成较大的影响，从而造成较大的误差。为了解决这个问题，试图构建一种新的函数g(f)来替换f，从而优化这些极端的函数值，构建一个良好的响应面模型。所构建的g(x)需满足3个条件：

(1)g(x)关于原点对称；

(2)g(x)严格增；

(3)g(x)0[5]。

构建g(x)为

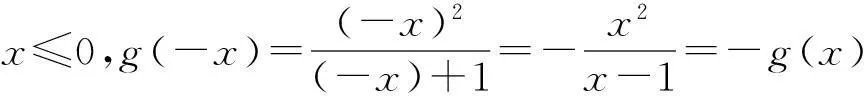
因此g(x)关于原点对称。

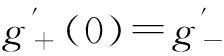
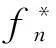
其中：循环长度N=5，n0表示初始迭代点的个数，n≥n0。

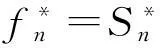
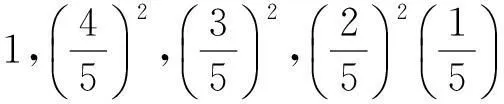
1.6下一个迭代点xn+1的选取

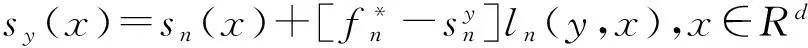
2重启动策略

采用SLHD方法生成初始点是因为它对高维低维问题都比较实用，基于SLHD的使用，有一些测试问题的CPU时间要短一些，而有一些测试问题的CPU时间就要长一些了，花费较长时间的原因可能是算法在一个错误的局部极小点处进行了较长时间的局部搜索，也就是说，采用的这种径向基插值算法在进行全局搜索时，由于局部搜索有可能失败，从而导致算法不能准确定位全局极小点。

为了解决这个问题，提出了一种重启动策略[2]，当算法连续多次迭代都没有取得明显进展，当没有改进的函数值的数量超过一个临界值之后，将使用一种新的SLHD重新开始搜索，通常将这个临界值设定为30，使用这种新的SLHD方法，可以使算法及时跳出局部最小值，加快收敛速度。

3结束语

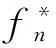
参考文献：

[1] BJÖRKMAN M,HOLMSTRÖM K.Global Optimization of Costly Nonconvex Functions Using Radial Basis Functions[J].Optimization and Engineering，2000,1(4):373-397

[2] ROMMEL G.Improved Strategies for Radial Basis Function Methods for Global Optimization[J].Journal of Global Optimization ,2007,37:113-135

[3] REGIS G,CHRISTINE A.Shoemaker.Constrained Global Optimization of Expensive Black Box Function Using Radial Basis Function[J].Journal of Global Optimization,2005,31:153-171

[4]YE K Q,LI W,SUDJIANTO A.Algorithmic Construction of Optimal Symmetric Latin Hypercube Designs[J].Joumal of Statistial Planning and Inference,2000,90(1):145-159

[5] REGIS G,CHRISTINE A.Shoemaker.A Quasi-multistart Framework for Global Optimization of Expensive Function Using Response Surface Models[J].Journal of Globa Optimization,2013,56: 1719-1753

[6] 林玉锋,陈璟,陈少飞,等.一种新颖的混合响应面优化方法[J].计算机应用研究,2012,29(6):2180-2183

An Optimization Method of Response Surface for ExpensiveBlack Box Function Optimization

QI Jing

(School of Mathematical Sciences,Chongqing Normal University,Chongqing 401331,Chongqing)

Abstract：In real scientific and engineering applications,problems on the expensive black box function often appear. In view of the expensive black box function global optimization,this paper researches the radial basis function and the response surface. is analyzed in theory,this paper proposes a new selection strategy. Different strategy selection leads to different search patterns,which affects the optimization effect.

Key words： expensive black box function; global optimization; radial basis function; response surface model; symmetric Latin hypercube design