基于动态灰神经网络的关键设备状态趋势预测

陈 涛 ，徐小力

（1.北京信息科技大学 机电系统测控北京市重点实验室，北京100192；2.北京信息科技大学 现代测控技术教育部重点实验室，北京100192）

机电设备特别是高端、大型、关键机电设备，其运行安全可靠性是国内外日益关注的重要问题。由于大型机电设备大量故障的演化往往经历发生、发展直至恶化的过程，而且大都有征兆可寻，采用科学的方法能够监测分析这一变化趋势。状态趋势预测能够通过分析设备历史和当前的运行状态，揭示随后的状态发展趋势特征，预测今后多长时间状态将达到不可接受的程度而应停机维修或进行针对性的维修。作为保障大型机电设备安全可靠运行的一项重要且难度较大的新技术，状态趋势预测的重要性正在逐渐被认识[1-3]。

针对状态趋势预测中小样本输入导致短历程预测精度低的难题，结合灰色模型处理小样本、贫信息的优势和神经网络良好的非线性逼近能力，提出一种动态灰神经网络智能趋势预测方法，构建相应的预测模型，并分析在工业现场风电机组趋势预测中的应用，验证其预测性能。

1 动态灰神经网络智能趋势预测

1.1 动态灰神经网络预测原理

在设备状态趋势预测中，大量精确的数据是实现高精度可靠预测的前提。然而由于工业现场关键设备不间断运行的特点、测试条件及技术水平等客观因素的制约，采集大量可靠性高的数据成为难题，小样本数据输入的预测更为常见。由于可获知的样本量少，要从这些少量的样本数据中获得趋势预测新信息的难度也就大大提高，小样本趋势预测成为研究难题。

小样本数据趋势预测的实质是在信息量有限的情况下，应用适当的建模方法和高效的算法对其中的潜在信息进行挖掘，从而找出信息间的规律性，再利用这些规律性对未知数据进行有效预测。灰色模型利用小数据、贫信息等已知信息，通过对“部分”已知信息的生成、开发，建立灰微分方程，能够实现对未知信息的有效预测[4]。以一维原始数列x（0）（k）（k=1，2，…，N 为数列中的数据个数）为例，采用灰色模型进行预测时，为增强规律性、弱化随机性，灰色模型通过一次正向累加运算生成规律性强化的新数列 x（1）（k）（k=1，2，…，N）。

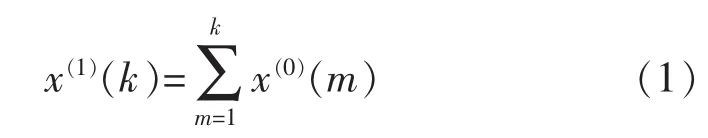
灰色模型预测对原始数据分布无要求，累加变换生成规律性强的新序列是其主要特点之一[5-6]。累加生成的逆变换为累减生成，是对原始数据依次做前后两数据相减的运算过程。累减生成中一次累加数列 x（1）与 x（0）之间的关系为

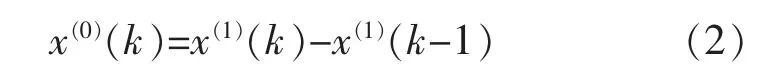
对新数列 x（1）k 建立灰微分方程为

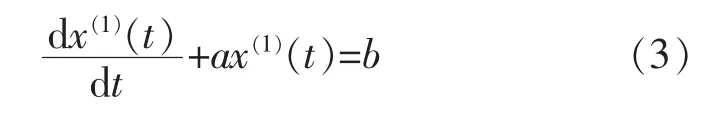
求解得到：

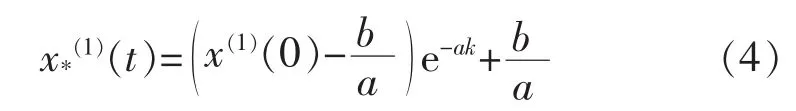
而对应的离散时间序列的响应函数为

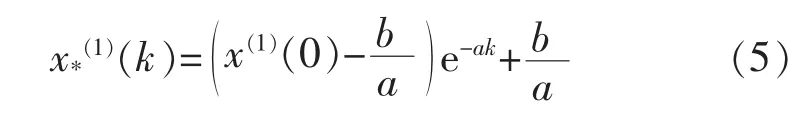
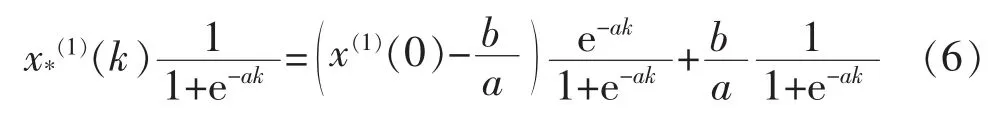
则有：

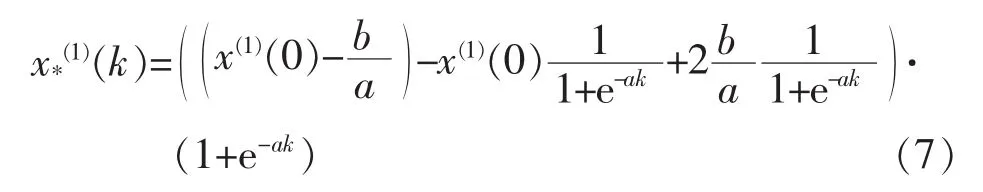
由累加生成公式和预测输出公式可看出，灰色模型仍是一种线性预测，当因变量与自变量之间存在非线性关系或是两者间的关系未知时，用灰色模型进行预测其精度并不高。

神经网络具有自组织、自学习和良好的非线性逼近能力，能够动态跟踪设备运行状态，揭示故障先兆的发展趋势。而动态神经网络是在前馈网络的基础上，增加了适于处理动态特性的反馈环节，使网络系统具有无限逼近任意非线性映射的能力，又能反映和设备运行状态的动态变化，非常适于对设备运行的动态信号进行智能预测[7]。

结合灰色模型处理小样本、贫信息的特性和动态神经网络智能预测的优点[8-9]提出一种新型的动态灰神经网络预测方法，动态灰神经网络在构造时考虑灰微分方程的参数，以灰色模型累加生成的样本对神经网络进行训练，能够揭示设备运行状态的内部本质，有效应对设备状态趋势预测的小样本问题，得到高精度的预测结果。

1.2 动态灰色神经网络预测模型

应用动态灰神经网络进行预测，为表达方便，对符号进行重新定义，原始数列 x（0）表示为 x（t），一次累加生成的序列 x（1）表示为 y（t），预测结果 x*（1）表示为z（t）。n个参数的灰神经网络模型的灰微分方程为

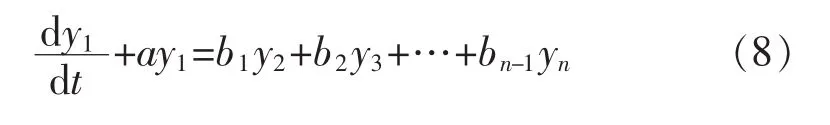
式中：y2，y3，…，yn为输入；y1为输出；a，b1，b2，…，bn-1为灰微分方程系数。

式（8）的时间响应为

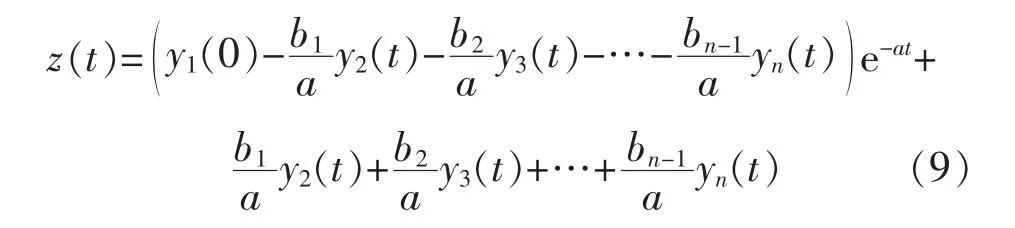
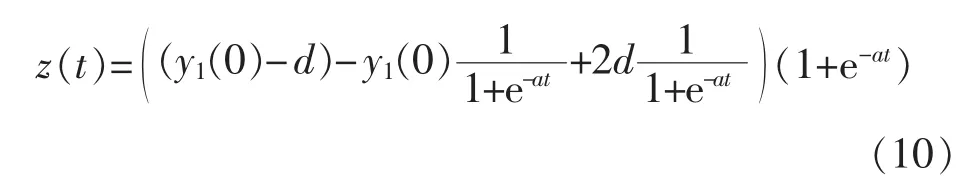
将式（10）映射到动态神经网络中，得到n个输入、1个输出的动态灰神经网络，以Elman网络为例[10-11]，网络拓扑结构如图1所示。

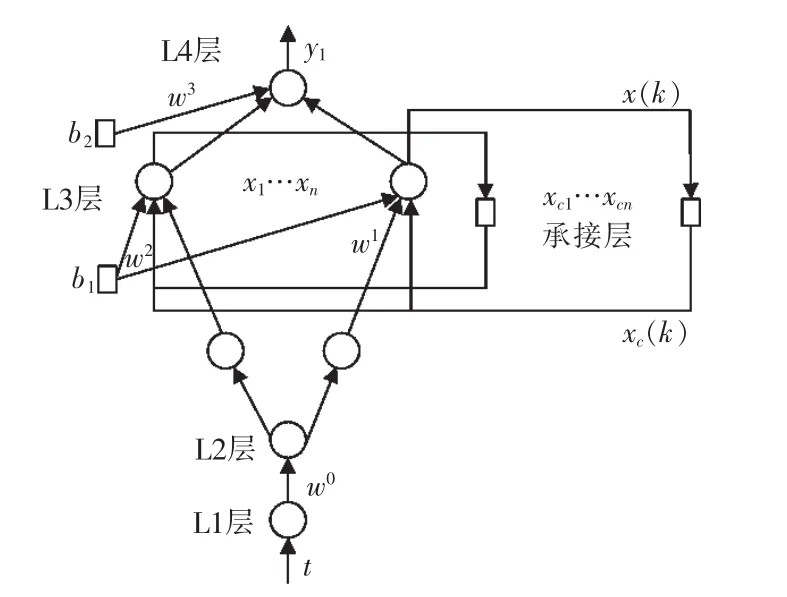
图1 动态灰Elman神经网络结构Fig.1 Structure of dynamic grey-Elman neural network

Elman神经网络是一种反馈神经网络，除具有输入层、隐含层和输出层外，Elman网络还增加一个承接层，作为一步延时算子，用于记忆隐含层单元前一时刻输出值，使其具有动态适应时变特性的能力。如图1所示，动态灰Elman神经网络的非线性状态空间表达式为

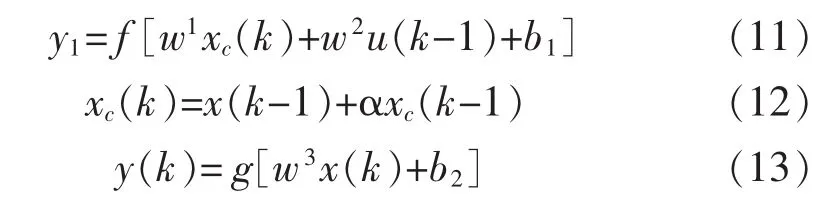
式中：k 表示时刻；y1为网络预测输出；L1、L2、L3、L4为网络的4层；承接层为动态Elman网络所特有的一个反馈层；x为隐含层输出；u为网络外部输入；xc为承接层输出；w0、w1、w2和 w3为各层间的连接权值；b1为输入层阈值；b2为隐含层的阈值。

动态灰神经网络模型的预测流程同神经网络预测流程类似，也包含神经网络构建，网络训练和网络预测3个部分，如图2所示，网络权值的初始化应用灰模型的参数设置：

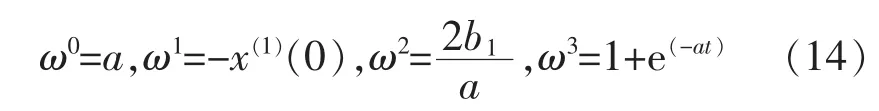
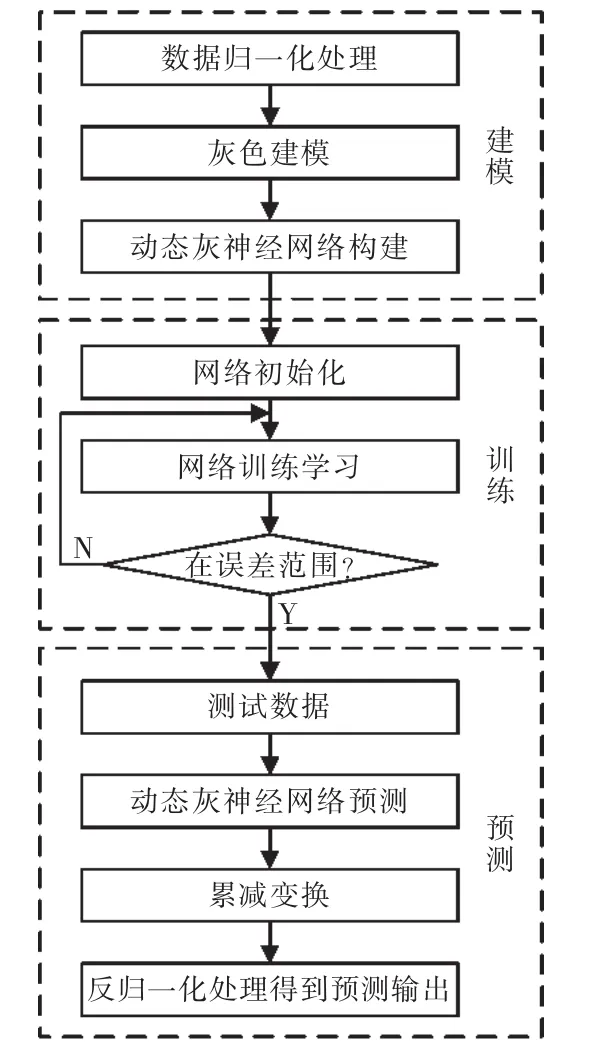
图2 动态灰神经网络预测流程Fig.2 Prediction process of dynamic grey-Elman neural network

在趋势预测中为减小样本输入量纲对预测结果的影响，将数据进行预处理归一化到［0，1］区间，xmax为该组变量的最大值，xmin为该组变量的最小值，归一化公式为

反归一化公式为

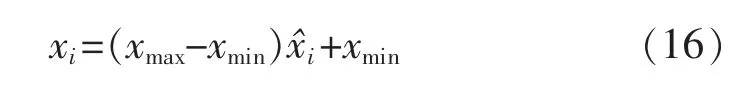
2 基于动态灰神经网络的风电机组趋势预测实例分析

以工业现场大型风电机组为研究对象，应用动态灰神经网络进行趋势预测实例分析。因风电机组的传动系统发生故障、造成停机的比例最高（高达20%），而齿轮箱作为风电机组关键的机械传动装置，一旦发生故障，将导致较长停机时间[12]。针对风电机组的故障特点，截取齿轮箱轴承测点的一段现场实测振动数据，对能体现整体工作状态的振动通频值，应用动态灰神经网络进行状态趋势预测分析。取前36天数据作为训练数据，后6天数据作为预测评价网络的预测性能（状态预测以天为单位）。

预测采用单步预测迭代形成的多步预测方式，样本数据的分段方法如表1所示，将训练数据分成段长度为（N+M）的有一定重叠的数据段，每一段的前N个数据作为网络的输入，后M个数据作为网络的输出。

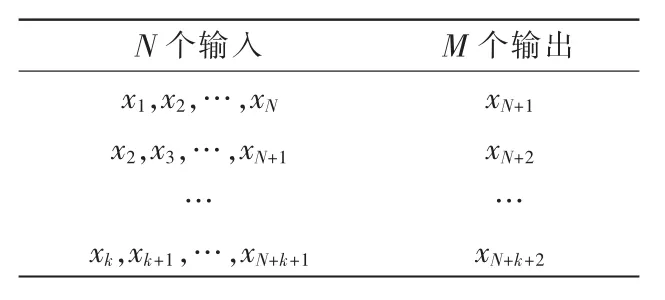
表1 单步迭代多步预测的数据分段Tab.1 Data segment of single step iterative multi-step prediction

预测中采用前6天的振动数据预测第7天的振动，根据输入、输出数据维数确定输入层为6维，输出层为1维，构建的灰神经网络结构为1-1-6-1，即L1层有1个节点，输入为原始数据序列，L2层有1个节点，L3层有6个节点，从第2个到第6个分别为5段设备运行状态的归一化数据，输出为预测振动通频值。为评价状态趋势预测的性能，选取均方误差（MSE）、平均相对误差（MAPE）作为模型的预测精度评价指标。计算公式为

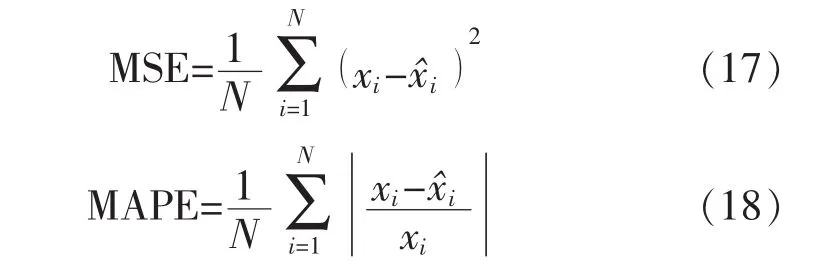
式中：N=6为预测数据个数；i为数据序号；x^i为预测数据值；xi为实际数据值。

应用动态灰神经网络进行6天的短历程趋势预测，网络训练误差如图3所示，趋势预测结果如图4所示。

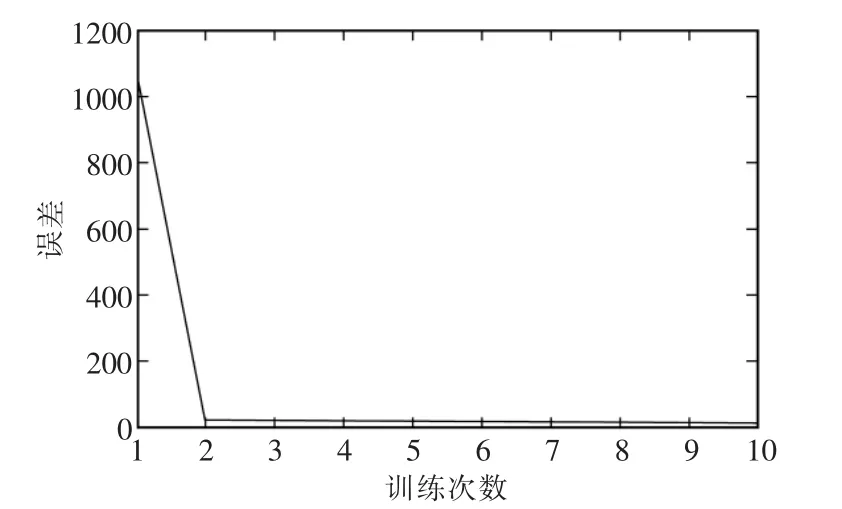
图3 动态灰神经网络的训练误差Fig.3 Training error of dynamic grey-Elman neural network

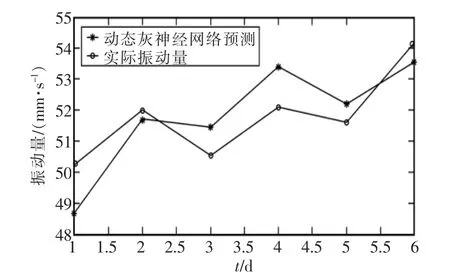
图4 动态灰神经网络的预测Fig.4 Prediction result of dynamic grey-Elman neural network

将动态灰神经网络与灰色模型和神经网络进行预测性能比较，结果如表2所示。

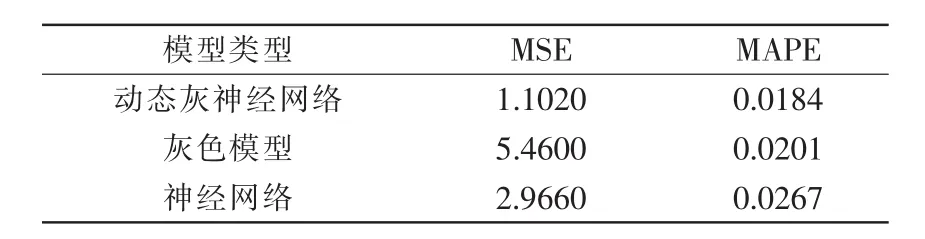
表2 动态灰神经网络与灰色、神经网络预测比较Tab.2 Prediction comparison of dynamic grey neural network with grey and neural network

由图3可以看出动态灰神经网络经过2次训练迅速达到误差要求，运算速度极快。结合图4和表2可以看出动态灰神经网络比灰色模型和神经网络预测性能均有大幅提高。结合理论分析，原因在于神经网络预测针对小样本输入，训练不充分，导致其在小样本短历程中误差较大；灰色模型由于数据间的非线性关系也导致其误差较大；而动态灰神经网络有效结合了灰色模型处理小样本、贫信息预测的优点，因而在小样本短历程预测中预测性能得到了提升。

3 结语

动态灰色神经预测模型结合了灰色模型和神经网络的优点，能够有效解决小样本短历程趋势预测精度低的难题。工业现场风电机组的实例分析验证了动态灰神经网络建模简单，运算速度快，对小样本输入预测精度高的优点，非常适合小样本数据的预测，能够为小样本数据短历程高精度的状态趋势预测提供一种新方法。

[1]徐小力，王红军.大型旋转机械运行状态趋势预测[M].北京：科学出版社，2011.

[2]何正嘉，蔡改改，申中杰，等.基于机械诊断信息的设备运行可靠性研究[J].中国工程科学，2013，15（1）：9-14.

[3]ANDREW K S J，DAMING L，DRAGAN B.A review on machinery diagnostics and prognostics implementing conditionbased maintenance[J].Mechanical Systems and Signal Processing，2006，20：1483-1510.

[4]邓聚龙.灰色控制系统[J].华中工学院学报，1982（3）：9-18.

[5]谢乃明，刘思峰.离散GM（1，1）模型与灰色预测模型建模机理[J].系统工程理论与实践，2005，25（1）：93-99.

[6]刘思峰，杨英杰.灰色系统研究进展（2004—2014）[J].南京航空航天大学学报，2015，47（1）：1-18.

[7]张际先，宓霞.神经网络及其在工程中的应用[M].北京：机械工业出版社，1996.

[8]吕宏辉，钟珞，夏红霞.灰色系统与神经网络融合技术探索[J].微机发展，2000（3）：3-5.

[9]袁景凌，钟珞，李小燕.灰色神经网络的研究及发展[J].武汉理工大学学报，2009（3）：91-93.

[10]Elman J L.Finding structure in time[J].Cognitive Sci，1990（14）：179-211.

[11]Wang Heyi，Gao Yi.Elman’s recurrent neural network applied to forecasting the quality of water diversion in the water source of lake taihu[J].Energy Procedia，2011，11：15.

[12]陈雪峰，李继猛，程航，等.风力发电机状态监测和故障诊断技术的研究与进展[J].机械工程学报，2011，47（9）：45-52.