分布式电源并网功率的控制研究

文献标志码：A

分布式电源并网功率的控制研究

张翔

(四川省电力公司计量中心,四川成都610000)

Research on the Power Control of Grid-connected Distributed Generation Power SystemZHANG Xiang

(Sichuan Electric Power Corporation Metering Center, Chengdu 610000, China)

摘要：分布式电源(Distributed Generation，DG)并网功率的控制多采用控制并网电流的方式来实现。当电网阻抗变化时，传统比例积分(Proportional-Integral，PI)控制的并网逆变器的系统稳态误差及并网电流总谐波畸变(Total Harmonic Distortion，THD)含量都会增大。基于鲁棒控制理论，本文提出了一种改进型的控制方法，通过合理的设计加权函数，使得在一定的电网阻抗变化范围内，控制系统在基波频率处具有很高的增益，而且具有足够的高频衰减特性。本文分析了电网阻抗变化对传统PI控制的系统稳定性的影响，给出了改进型控制方法的设计原理。仿真及实验结果验证了此改进型控制器的有效性。

关键词：分布式电源；比例积分控制器；并网逆变器；鲁棒控制；总谐波畸变

文章编号：1007-2322(2015)05-0079-05

中图分类号：TM464

收稿日期：2014-11-28

作者简介：张翔(1987—)，男，硕士，工程师，研究方向为电力电子技术在电力系统中的应用，E-mail:guaishiqin@sina.com。

Abstract：The power of the distributed generation in the grid-connected mode was usually controlled by the grid current. As the grid impedance changes, the steady-state errors and the content of total harmonic distortion will increase when conventional proportional-integrator controller is used. Based on the robust control technique, an improved control scheme is proposed in this paper. By properly designing the weighting functions, the proposed controller exhibits high gains at the vicinity of the fundamental frequency and the sufficient high-frequency attenuation characteristics within a certain range of the grid impedance changes. In this paper, the influence of the grid-impedance variations on system stability is analyzed when conventional proportional-integrator controller is used, and the design principle of the improved control scheme is given. In the end, the simulation and experimental results verify the effectiveness of the proposed scheme.

Keywords：distributed generation; proportional integral controller; grid-connected inverter; robust control; total harmonic distortion

0引言

近年来，基于太阳能、风能、燃料电池等各种可再生能源的分布式电源的发展成为研究热点[1]。分布式电源组成的微电网一般有两种运行方式：并网运行和孤岛运行。并网运行状态下，微电网的电压是由公共电网所提供的相对稳定的电压幅值和频率决定的，因此控制分布式电源的功率通常采用控制其并网电流的方式来实现，并网电流的总谐波畸变含量是衡量分布式电源并网运行的一项重要指标。

传统并网电流控制方法中，通常采用三相静止坐标下的PI控制加上电网电压前馈的方法，但由于PI控制存在较大的稳态误差而不能取得满意的控制效果[2]。还有可以采用同步旋转坐标下的PI控制方法，此法由于坐标之间转换引入误差而影响控制效果，且难以应用于单相并网系统[3]。文献[4]中提出的现在应用比较多的比例谐振控制器(Proportional-resonant, PR)，其在特定频率点具有较高增益，可以很好地实现零稳态误差的跟踪效果，但是其没有足够的高频衰减来保持系统稳定性。文献[5]中提出了一种导纳补偿器结合PR控制器的控制方法，把逆变器输出电流作为反馈控制量，使得控制系统简化为一阶系统，可保持控制环的高增益和高带宽，不过由于输出滤波电容和电网阻抗组成的谐振网络，因此在谐振频率处的逆变器输出电流都要被放大，这样会加大电网电流的谐波分量。文献[6]提出把电网电流叠加部分滤波电容电流作为反馈控制量，这样通过零极点对消，也可将控制系统简化为一阶系统，但是零极点对消需要准确知道电网阻抗及逆变器阻抗，对于公共电网来说，阻抗是随时在变化的，现在绝大多数的研究都是假设电网阻抗为零的理想电网，因此电网阻抗大范围的变化对分布式电源控制稳定性的影响已经受到了广泛的关注[7]。

本文首先分析了电网阻抗对传统PI控制的影响，在此基础上提出了一种基于鲁棒控制理论的改进型控制方法，在一定的电网阻抗变化范围内，通过合理设计加权函数，使得改进型控制器在基波频率处具有较高的增益，且具有足够的高频衰减来保持系统稳定性。加权函数的设计将被详细讨论，仿真及实验结果验证了改进型控制方法的有效性。

1电网阻抗对传统PI控制的影响

三相静止坐标下的PI控制加上电网电压前馈[8]，这种传统的控制并网电流的方法，在考虑忽略控制延时以及输出电压可以通过前馈回路完全补偿的情况下，其简化系统图如图1所示。其中，iref表示标准参考电流信号，igrid为电网电流，Kp为PI控制的比例系数，Ki为PI控制的积分系数，uL为输出电感上的电压，Lf为输出电感的电感值，iL为输出电感上的电流，Cf为输出电容的电容值，ugrid为电网电压，Lgrid为电网等效电感，rgrid为电网等效电阻。

该控制系统的电流闭环传递函数如下：

(1)

图1　三相静止坐标下PI控制的简化控制框图

根据传递函数，图2和图3分别给出了不同电网阻抗情况下系统的根轨迹图。

图2　r grid为定值，L grid从0.1μH变化到100μH的 系统根轨迹图

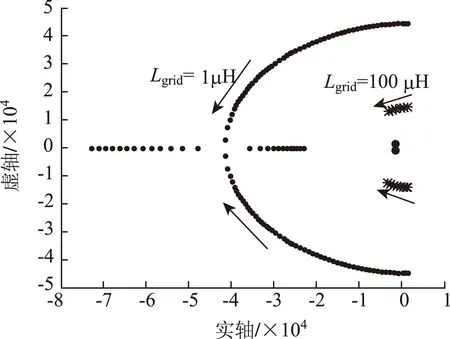
图3　L grid为定值1μH及100μH，r grid从0.1mΩ 变化到1Ω的系统根轨迹图

图2是rgrid为定值1 mΩ，Lgrid从0.1μH变化到100μH的系统根轨迹图，图3是Lgrid为定值1μH及100μH，rgrid从0.1mΩ变化到1Ω的系统根轨迹图。从图2和图3可以看出，系统的特征根随着Lgrid的增大向右边平面移动，随着rgrid的增大向左半平面移动。这表明当电网阻抗增加尤其是感性阻抗增加时，主导极点会向虚轴和右半平面移动，这样将导致系统不稳定。

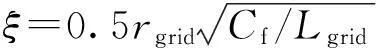
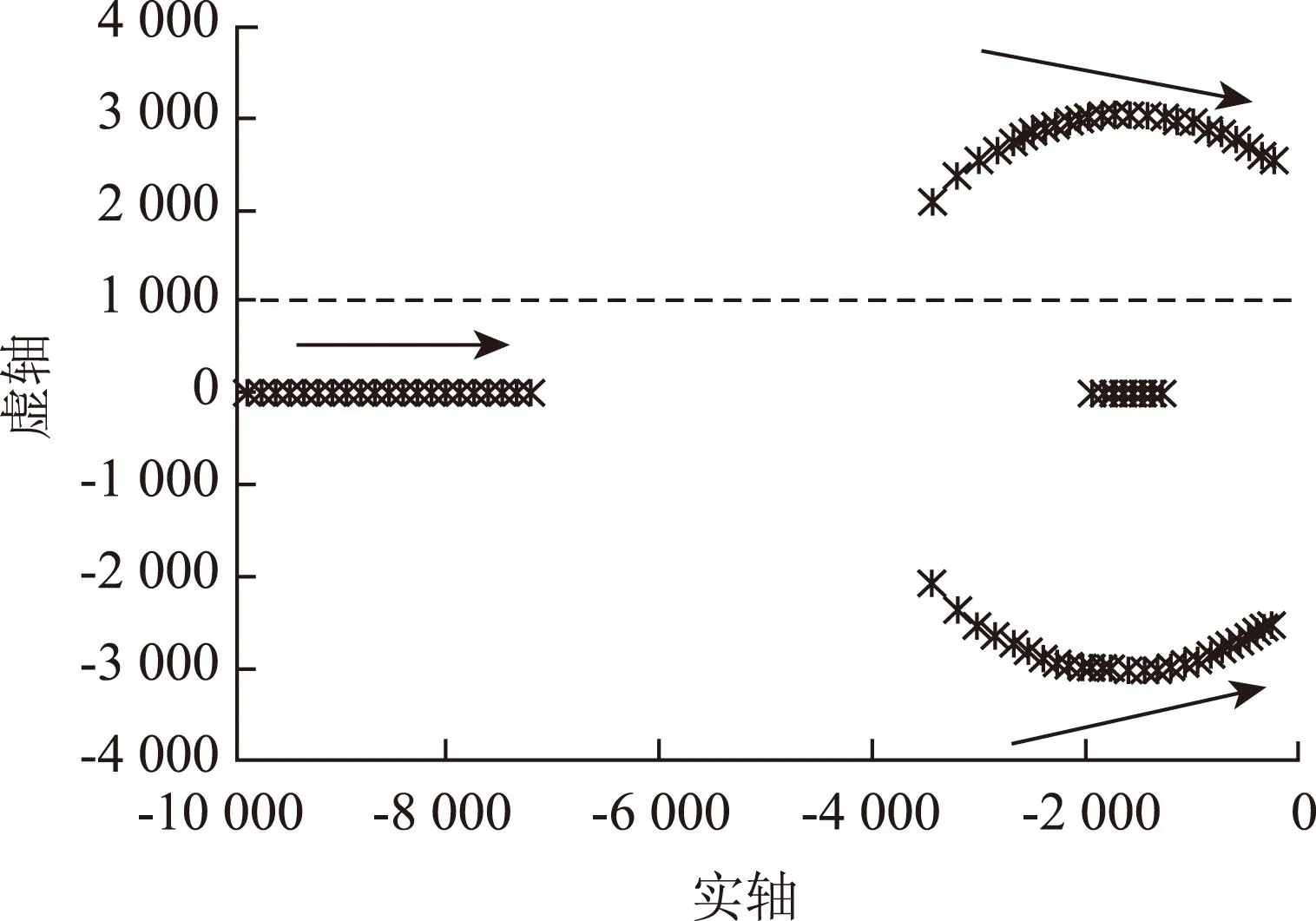
图4　ξ为定值1，L grid从0.1μH变化到100μH的 系统根轨迹图

从以上可以看出，电网阻抗尤其是感性阻抗增大时，传统PI控制将无法满足控制系统稳定性的要求。

2改进型控制器的设计

为了能在一定电网阻抗的变化范围内保持系统的稳定性，且能获得满足要求的电流THD含量，本文提出了一种基于鲁棒控制理论[9]的改进型控制器L(s)，系统控制框图如图5所示，其中L(s)包含了图1中的物理环节1/Lfs，使得L(s)只需补偿一个二阶系统。图6为带加权函数的鲁棒控制结构，其中，w是外部基准的输入，u是控制的输入，x是控制的输出，y是观测量的输出，G(s)是控制对象，W1(s)是误差跟踪加权函数，W2(s)是控制器传递函数，W3(s)是鲁棒性加权函数。

图5　基于鲁棒控制的系统控制框图

图6　带加权函数的鲁棒控制结构

鲁棒控制器的设计是基于混合灵敏度的方法来合成的，为了得到稳定的控制器L(s)，则需要使得控制器从外部基准输入w到控制的输出x的增益小于1，即

(2)

其中P(s)=1/(1+G(s)L(s))是灵敏度传递函数，表示外部基准输入到输出的传递函数；Q(s)=G(s)L(s)/(1+G(s)L(s))即补灵敏度函数，表示参考输入到误差的传递函数，且Q(s)+P(s)=1。可以看出混合灵敏度的方法就是通过合理设计P(s)和Q(s)的加权函数W1(s)和W3(s)来确定回路形状的。因此加权函数就在一定程度上决定了系统所需求传递函数的频率特性的形状，其直接反映出了系统的各种性能指标。通常情况下，设计误差跟踪加权函数W1(s)在控制带宽内具有足够高的增益以达到良好的抗扰动及误差跟踪性能；设计鲁棒性加权函数W3(s)在控制带宽外具有足够高的增益以确保系统的稳定；而控制器传递函数W2(s)则可以选择一个较小的定值或为空[10]。

设计W1(s)时，考虑到系统小的跟踪误差是跟踪公网正弦信号，这也就是说P(s)在基波频率处增益很小，而且根据式(2)可以知道，P(s)的频率响应由W1(s)决定，所以W1(s)需要在基波频率处具有较高的增益，在其他频率具有较低的增益。因此本文选择了一个标准的二阶传递函数[10]：

(3)

式中：ω为基波频率，k1和ξ提供了控制的自由度，当ξ趋近于零时，此传递函数的谐振峰会很高，但是更狭窄，将类似于标准的PR控制器。

设计W3(s)时，考虑其反映的是系统的鲁棒性要求即高频特性要求，参照常规鲁棒性控制的不确定性加权函数的设计方法：首先根据控制对象G(s)得到额定控制对象GN(s)，即把G(s)中的电网等效阻抗替换为相对额定条件下的阻抗值；然后根据阻抗变化引起的系统不确定性表示为乘性不确定性[11]，求出控制模型的不确定性为

(4)

式中：Δ(s)为控制模型的不确定性；Gc为系统扰动对应的参数改变；σ(K)表示传递函数K的奇异值；当Gc改变最大时，即为最坏情况的Δ(s)，则确定了最大的扰动范围。这时为了达到扰动范围内要求的鲁棒性，设计W3(s)的奇异值落在这个最坏情况的值上。

这样，设计好W1(s)，W2(s)，W3(s)后，使用Matlab软件中的鲁棒控制工具箱即可合成一个满足要求的鲁棒控制器L(s)。

3仿真及实验结果

为了验证改进型控制器的性能，本文分别采用传统PI和改进型控制器搭建控制系统，对分布式电源系统进行了仿真和实验。系统参数如下：开关频率及采样频率均为10kHz，输出滤波电感Lf为1mH，输出滤波电容Cf为50μF，电网等效额定电阻rgridN为0.15Ω，电网等效额定电感LgridN为0.1mH，额定输出功率为10kVA，假设电网等效电阻的变化范围是0.05~0.2Ω，电网等效电感的变化范围是0.05~0.3mH。根据上文介绍的设计方法，本文对W1(s)，W2(s)，W3(s)的具体设计参数如下：W1(s)中的k1取2，ξ取0.01；W2(s)取0.1；W3(s)为

(5)

图7为PI控制的系统仿真结果，图8为改进型控制的系统仿真结果，其中PI控制中Kp取3，Ki取3 000，均是电网阻抗在0.2s时从额定值分别变为：rgrid=0.2Ω，Lgrid=0.3mH。

图7　PI控制系统仿真结果

图8　改进型控制系统仿真结果

图9为电网阻抗为额定阻抗时PI控制的系统实验结果，图10为电网阻抗为0.2Ω和0.3mH时PI控制的系统实验结果。图11为电网阻抗为额定阻抗时改进型控制的系统实验结果，图12为电网阻抗为0.2Ω和0.3mH时改进型控制的系统实验结果。

从仿真及实验结果都可以验证前文的分析，传统的PI控制在电网阻抗尤其是感性阻抗增加时，并网电流会出现不稳定的现象，而改进型控制器在电网阻抗变化范围内能有效地保持系统的稳定，得到良好的并网电流。

图9　电网阻抗为额定阻抗时PI控制的 系统实验结果

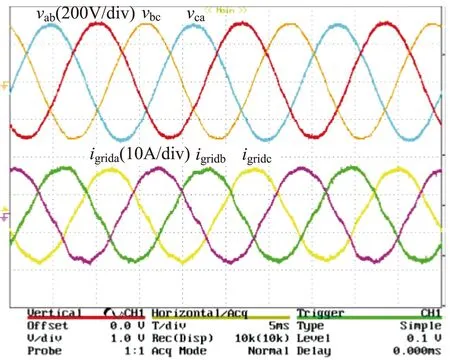
图10　电网阻抗为0.2Ω和0.3mH时PI控制的 系统实验结果

图11　电网阻抗为额定阻抗时改进型控制的系统实验结果

图12　电网阻抗为0.2Ω和0.3mH时改进型控制的 系统实验结果

4结论

本文基于鲁棒性控制理论提出了一种改进型的控制器应用于分布式电源的并网功率控制中，阐述了其设计原理方法，并与传统PI控制方法进行了对比分析。

最后通过仿真及实验验证了该方法在电网阻抗变化时的有效性和优越性，且该方法是基于三相静止坐标，因此可以应用于单相及三相系统的场合。

参考文献

[1]Ali Ipakchi，Farrokh Albuyeh. Grid of future[J]. IEEE Power and Energy Magazine，2009，7(2)：52-62.

[2]Brod D M，Novotny D W. Current control of VSI-PWM inverters[J]. IEEE Trans. Ind. Appl.，1985，21(4)：562-570.

[3]Twining E，Holmes D G. Grid current regulation of a three-phase voltage source inverter with an LCL input filter[J]. IEEE Trans. Power Electron.，2003，18(3)：888-895.

[4]Teodorescu R，Blaabjerg F，Liserre M，Loh P C. Proportional-resonant controllers and filters for grid-connected voltage-source converters[J]. IEE Proc.-Electr. Power Appl.，2006，153(5)：750-762.

[5]Park S，Chen C，Lai J，Moon S. Admittance compensation in current loop control for a grid-tie LCL fuel cell inverter[J]. IEEE Trans. Power Electron.，2008，23(4)：1716-1723.

[6]Shen Guoqiao，Xu Dehong，Cao Luping，Zhu Xuancai. An improved control strategy for grid-connected voltage source inverters with an LCL Filter[J]. IEEE Trans. Power Electron.，2008，23(4)：1899-1906.

[7]Liserre M，Teodorescu R，Blaabjerg F. Stability of grid-connected PV inverter with large grid impedance variation[C]. IEEE Power Electronics Specialists Conference，2004：4773-4779.

[8]Li Y W，Vilathgamuwa D M，Loh P C. Design，analysis，and real-time testing of a controller for multibus microgrid system[J]. IEEE Trans. Power Electron.，2004，19(5)：1195-1204.

[9]Zames G. Feedback and optimal sensitivity：model reference transformations，multiplicative seminars，and approximate inverses[J]. IEEE Trans. Automatic Control，1981，26(2)：301-320.

[10]Li Y W，Vilathgamuwa D M，Loh P C. Robust control scheme for a microgrid with PFC capacitor connected[J]. IEEE Trans. Ind. Appl.，2007，43(5)：1172-1182.

[11]Gu D W，Petkov P H，Konstantinov M M. Robust control design with Matlab[M]. Springer-Verlag London Limited，2005.

(责任编辑：林海文)