电涡流缓速器数学模型的构建与验证

马毅

(中国汽车工程研究院股份有限公司,重庆 140022)

电涡流缓速器数学模型的构建与验证

马毅

(中国汽车工程研究院股份有限公司,重庆 140022)

摘要：构建了电涡流缓速器的制动功率和制动力矩的数学模型,构建过程中考虑了转子在低速时磁饱和效应和高速时涡流的去磁效应,以及转子和定子间隙对磁场的影响。对试验数据进行了对比,结果表明:电涡流缓速器理论功率和实测值最大相差4.3%,理论制动扭矩和实测值最大相差6.3%,理论值和实测值基本一致。

关键词：电涡流缓速器;制动功率;制动力矩

收稿日期：2015-07-14

作者简介：马毅(1987—)，男，河南内乡人,工程师,主要从事排放检测方面的研究工作。

中图分类号：TH123

文献标识码：A

文章编号：编号：1674-9944(2015)09-0297-04

Abstract:This article constructs the mathematical model of eddy current retarders' braking power and braking torque.In the process of the construction,the rotors' magnetic saturation effects and eddy currents' demagnetization effects are considered in the mathematical model of the eddy current retarder when its speed is low and high.In addition,the effect of the space between the rotor and stator on the magnetic field is also considered.Through the comparison with the experimental data,the results indicate that the maximum difference of the eddy current's theoretical power and test value is 4.3% and that of the theoretical torque and measured value is 6.3%,which mean that the theoretical value and test value are basically the same.

1引言

电涡流缓速器在一些大中型客车及货车上使用,主要起到辅助制动作用。它是根据法拉第电磁感应定律,转子在通有电流的定子中高速旋转,产生阻力,从而对车辆产生制动力。由于大中型客车及货车载重大,在坡道地区或者道路变化大的地方,长时间的制动很容易使车辆摩擦片过热,使得制动阻力下降,严重者可能导致紧急时刻刹车失灵从而产生危险[1]。电涡流缓速器的使用可以很好避免此类事件发生,转子和定子之间存在间隙,不直接接触,不存在磨损;采用电流驱动,动作响应快。电涡流缓速器担负着汽车上80%的制动效果,可以使车辆摩擦片一直处于冷却状态,提高汽车的行驶安全性[2]。

本文对电涡流缓速器的数学模型进行了重构,考虑了转子在低速时磁饱和效应和高速时涡流的去磁效应,以及转子和定子间隙对磁场的影响,并通过与实际试验数据进行对比验证,从而为电涡流缓速器的设计和精确控制提供理论依据。

2电涡流缓速器数学模型的建立

2.1　制动功率的理论推导

图1为电涡流缓速器的磁场模型图,其中阴影部分为定子,圆盘为转子。定子为线圈绕着磁轭行程,在实际使用中线圈通上电流即可产生磁场;转子直接为转子盘,车辆行驶带动转子盘旋转。

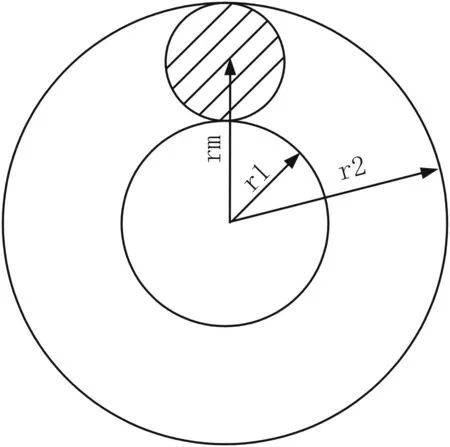
图1　磁场简化模型

当转子盘旋转一周时,一个铁心所对应的旋转面积

S=π(r22-r12)=πd·2rm

(1)

式中d为磁轭的直径,m。相应的磁通量为Φ=BS,在时间t下:

Φ=BSft

(2)

式中φ为磁通量,Wb;B为磁感应强度;S为旋转一周面积, m2;f为转子盘旋转频率,Hz;t为时间,s。

根据法拉第电磁感应定律,磁场变化产生的感应电动势ε为:

(3)

由于铁心下面对应的涡流环为圆形,计算涡流环电阻时建立如图2的模型。

图2　电阻计算模型

此圆环电阻:

(4)

式中ρ为转子盘的电阻率,Δh为涡流的集肤深度。圆环上的瞬时功率为:

(5)

涡流环上直径为d的瞬时功率:

(6)

磁轭为Ng,则电涡流缓速器涡流损耗功率即为制动功率:

(7)

式中Ng为磁轭个数。

2.2　制动力矩

2.2.1涡流的集肤深度计算

(8)

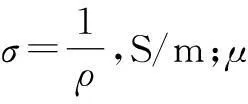
式中μr为转子盘相对磁导率,低碳钢一般为100~500;μ0为真空磁导率,μ0=4π×10-7H/m。

2.2.2气隙中的磁感应强度

由于转子盘在磁场中高速旋转,根据法拉第电磁感应定律,在转子盘中会产生阻碍磁通量变化的反向电动势,即有涡电流产生[5],因此磁路中的磁动势会有变换,不再是φm,而是比φm小的一个值φm1。即有:

Φm1=Φm-Φe

(9)

式中φm为励磁绕组的磁动势,A;Φe为涡流产生的等效磁动势,A。其中:

Φm=NIc

(10)

式中N为励磁绕组的匝数;Ic为绕组中的电流,A,其中:

ΦE=keIe

(11)

式中ke为折算系数,通常取ke=2;Ie为所计算区域涡流的有效值,A。图3为电涡流缓速器的磁场模型,计算Ie时参考此模型。

图3　电涡流缓速器的磁场模型

图中阴影部分面积I为一个磁轭所对应的磁通面积,其磁通量为φ1=BSp。从图中可以看出,在转子盘旋转过程中,磁通量Φ是不断变化的。图中Ⅰ→Ⅱ→Ⅲ为一个磁轭位置的变化过程,对应的磁通量变化为:Φ1→0→-Φ1→0→Φ1,可以认为其是按Ф1=BSpcosωct变化的。通过此环的磁通为:

Φ1=πr2B cosωct

(12)

式中Φ1为单个铁心对应的磁通量;B为磁场中磁感应强度,T;ωc为磁场变化角速度,rad/s。磁场变化角速度:

(13)

式中Np为磁极对数;n为转子盘的转速,r/ min。由此可知,感应电动势为:

(14)

把(4)代入得:

(15)

则圆形区域内的顺势涡流:

(16)

式中:

(17)

圆形区域的涡流有效值:

(18)

由于磁阻的存在,可得磁路中磁通量:

(19)

其中Rm为磁路中的总磁阻。由于转子盘、磁轭和铁心的使用材料相对磁导率较高,而空气的相对磁导率μr≈1,相对于气隙lg来说,可忽略不计[6]。故磁路中的总磁阻为:

(20)

将式(9)、(10)、(11)、(18)、(20)代入(19),可计算得电涡流缓速器中,考虑了涡流去磁效应及磁阻共同作用下的磁感应强度:

(21)

由于(6)中的Rm只考虑了空气的磁阻,实际上当铁心磁通量很大,涡流的去磁效应还很小时,转子盘就会产生磁饱和,此刻转子盘的磁阻就会趋近于无穷大,低碳钢磁饱和时的磁感应强度为2.2T,所以:

(22)

2.2.3制动力矩

根据P=Tω,有式(7)可得:

(23)

式中T为制动力矩,N.m;ω为转子盘旋转角速度,rad/s。该式为电涡流缓速器所产生的制动力矩与结构参数(lg、d、rm、Ng、Np),励磁线圈参数(N、I),材料参数(、μr)及转子盘旋转角速度ω等变量之间的关系。

3电涡流缓速器数学模型与实验数据对比分析

图4为电涡流缓速器实物照片,其他相关参数如下所示[7]:最大制动功率325kW (试验值),最大制动力矩Tmax为1531N.m(试验值),临界转速n约为520r/ min,磁隙lg=1.4 mm,磁极面积Sp=10652m m2;平均半径rm=191 mm;内环半径r1=140 mm;外环半径r2=238 mm;总质量m=32 kg;磁动势Φm=10500A,磁极对数Np=4(Ng=16),转子盘的电阻率ρ= 0.97×10-7Ω·m。

图4　缓速器实物照片

表1、表2为电涡流缓速器不同转速下对应的功率和扭矩的实验数据。

表1　转速和功率实测值

表2　转速和扭矩实测值

将电涡流缓速器的参数带入公式(7),可得不同转速n下对应的电涡流缓速器的功率P,其中涡流的集肤深度△h和磁感应强度B分别参考公式(8)和(22)。图5为电涡流缓速器理论计算值和实测值之间的对比关系图,从图中可以看出,理论计算值和实测值基本一致,最大误差为 4.3%。

由公式(8)、(22)、(23)可得电涡流缓速器不同转速n下对应的理论制动力矩T。图6为理论制动力矩和实测值之间的对比图。从图中可以看出理论制动扭矩和实测值最大相差6.3%。但当转速提高时,制动力矩有所下降,这主要是由于转速提高,涡流磁阻增大,从而降低了电涡流缓速器的效应。

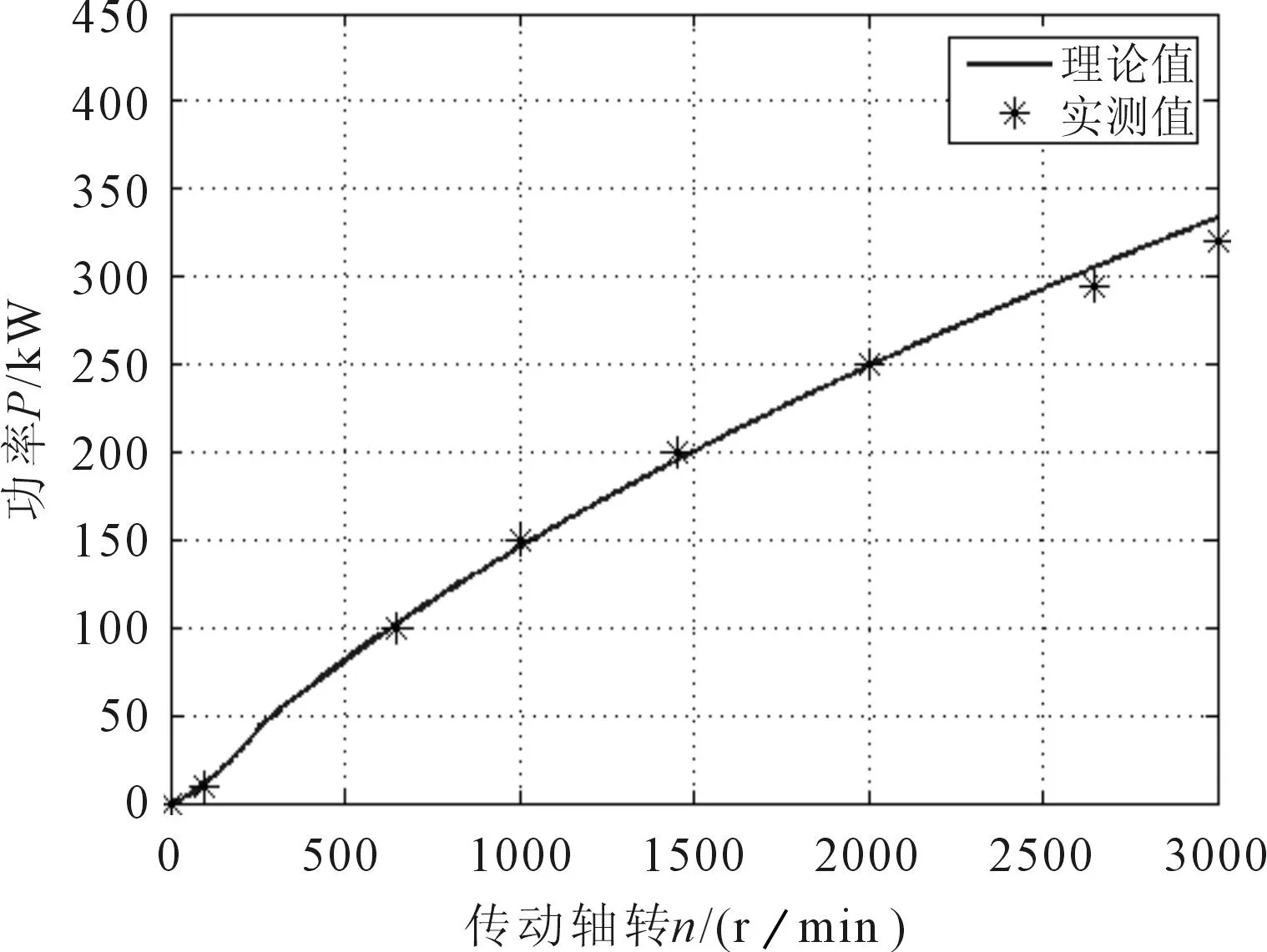
图5　功率

根据图5和图6,电涡流缓速器的理论功率、理论制动力矩和实测值对比分析可以看出,电涡流缓速器的数值计算结果和实测值基本一致。电涡流缓速器的数值模型在建立过程中考虑了低碳钢的磁饱和效应,修正了在低速过程中,由于磁场过大,而实际磁轭的磁通量有限这一现象,使得理论值和实测值更为贴近;考虑了涡流的集肤效应,使得不同转速下磁阻更加符合实际情况;另外考虑了电涡流缓速器磁隙的影响,使得模型可以适应不同电涡流缓速器的计算,增加了模型了适应普遍性。

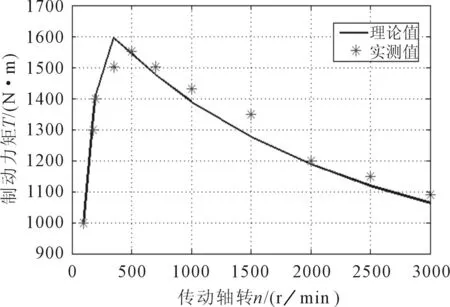
图6　扭矩

参考文献：

[1] 汽车之家.电涡流缓速器[EB/OL].[2015-04-26].http://car.autohome.com.cn/shuyu/detail_13_14_766.ht mL,2015-04-26.

[2] 韩锋钢.商用车辆制动发展趋势[J].商用汽车,2000(6).

[3] 冯慈璋,马西奎.工程电磁场导论[M].北京:科学出版社,2001:127~138.

[4] 左俊业,田学义.感应子式涡流测功机的有效参数计算[J].电子技术,1979(2):31~42.

[5] 张逸成,沈玉琢,庞乾麟,等.旋转涡流制动器电磁机构的设计研究[J].铁道学报,1986(6):22~27.

[6] 孙为民,张跃明,吴兵波.电涡流缓速器制动力矩计算的新方法[J].现代机械,2015(4):21~29.

[7] 山东交通学院.电涡流缓速器研究开发和应用[R].济南:山东交通学院,2008(9):29~30.

The Construction and Verification of Eddy Current Retarders'

Mathematical Model

Ma Yi

(ChinaAutomotiveEngineeringResearchInstituteCo.,Ltd.,ChongQing140022,China)

Key words:eddy current retarders;braking power;braking torque