面向储舱结构设计的晃荡冲击荷载实验研究

第一作者陈晓东男，硕士生，1987年生

通信作者岳前进男，教授，博士生导师，1958年生

面向储舱结构设计的晃荡冲击荷载实验研究

陈晓东1,3，卫志军1,2，岳前进1，阮诗伦1，赵小西1

(1.大连理工大学工业装备结构分析国家重点实验室，大连116023；2.挪威科技大学船舶与海洋结构研究中心，挪威特隆赫姆7049； 3.深圳海油工程水下技术有限公司，深圳518067)

摘要：薄膜型船载液化天然气储舱设计中的一个关键力学问题是对液体晃荡引起的冲击荷载的评估。晃荡冲击载荷主要包括晃荡冲击荷载的幅值，上升和持续时间以及荷载三角脉冲的偏斜度等参数。室内大比尺晃荡模型实验是评估晃荡冲击荷载的有效方法。以二维矩形液舱为模型，在大吨位六自由度运动平台开展了一系列不规则激励下的晃荡冲击荷载实验研究。研究结果表明：由于液体与气体的相互作用，导致晃荡冲击荷载具有幅值较大且冲击上升时间较短的特点，可能导致舱壁产生较大的响应。采用统计学的方法分析了晃荡冲击荷载的参数；此外，定量地提出了长期不规则激励下，由荷载峰值、上升和持续时间以及偏斜度的组成的三角脉冲荷载模型，该模型可为储舱舱壁结构设计和有限元分析提供荷载参考。

关键词：晃荡荷载；模型实验；冲击荷载参数；脉冲荷载模型

基金项目：国家科技重大专项项目(2011ZX05026-006-06)；创新研究群体基金资助(50921001)

收稿日期：2014-03-31修改稿收到日期：2014-10-11

中图分类号:U661.71文献标志码：A

Experimental investigation on sloshing impact pressure for tank structure design

CHENXiao-dong1,3,WEIZhi-jun1,2,YUEQian-jin1,RUANShi-lun1,ZHAOXiao-xi1(1. State Key Laboratory of Structural Analysis for Industrial Equipment, Dalian University of Technology, Dalian 116023, China; 2. CeSOS, Department of Marine Technology, Norwegian University of Science and Technology, Trondheim 7049, Norway; 3. COOEC Subsea Technology Co., Ltd, Shenzhen 518067, China)

Abstract:Sloshing impact pressure is a key issue in the structural design of the membrane type Liquefied Nature Gas (LNG) carriers. The parameters of sloshing impact load includes its magnitude, rise time, duration and skewness. Experimental investigation on a large-scaled sloshing model is the most reliable approach to determine impact loads. A series of tests on a 2D rectangular tank subjected to irregular excitations were performed on a hexapod test rig. The experimental results show that due to the interaction between liquid and gas, the peak pressure exhibits large magnitude and short rise time, which might induce large structural dynamic response. The key parameters of sloshing impact load were analyzed by using a statistical method. An idealized triangular impact pressure was introduced as a quantitative long-term irregular excitation to provide a simplified model of the impact load which contains all the essectial parameters of magnitude, rise time, duration and skewness of the impact pressure. This gives a reference to the structural design of LNG tanks.

Key words:sloshing load; model test; parameters of impact load; idealized triangular impact model

超大型浮式液化天然气生产储卸装置(Floating Liquid Nature Gas，FLNG)的研发与建造将会大大提升深、远海天然气开发模式的先进性和经济性。在复杂海洋环境荷载以及储舱内连续变化的装载水平下，其大容积薄壁储舱内的液体晃荡冲击问题愈加显著，对储液舱结构设计提出了更高的要求[1-3]。因此，准确有效地评估舱内晃荡冲击荷载的分布及特性对于储舱结构设计至关重要。

储舱内液体晃荡往往伴随着复杂的水动力现象，如水跃，波的破碎，气泡效应等，其高度的非线性使得解析方法和数值计算在预测晃荡冲击荷载时具有一定的局限性。因此，室内大比尺晃荡模型实验仍然是评估储舱晃荡冲击荷载最有效且应用最广泛的研究方法[4-10]。

由晃荡冲击荷载引起的储舱结构动响应主要与荷载峰值的大小、上升和持续时间以及荷载脉冲的偏斜度等参数相关[11-13]。由于不规则的外激激励和晃荡本身的随机特性，冲击荷载峰值主要通过统计学的方法来评估：运用三参数Weibull分布，广义Pareto分布和广义极值分布可以对冲击荷载峰值的超越概率密度进行拟合，并且通过K-S法检验其分布拟合优度[14-16]。然而，超越概率分布只能反映出晃荡冲击荷载的部分信息，荷载上升和持续时间与液舱结构自振周期的关系以及荷载脉冲的偏斜度都未能得到评估，即概率分布不能给出一个完整的供储舱结构设计的冲击荷载形式。因此，通过晃荡模型实验研究得到既包含荷载峰值大小，又包含上升和持续时间以及荷载脉冲的偏斜度等信息的晃荡冲击荷载对储舱的结构设计更为关键。

本文以二维矩形液舱为研究对象，在大吨位六自由度运动平台开展了长期的不规则外激激励下的晃荡模型实验研究，选择冲击荷载冲击率较大的三个测点位置，统计晃荡冲击荷载的上升和持续时间，分析其与储舱结构响应的关系；计算冲击荷载三角脉冲的偏斜度，分析不同偏斜度下储舱内流体冲击的差异；本文定量地提出储舱结构设计时所需要的包含荷载峰值大小、上升和持续时间以及脉冲偏斜度下最危险的冲击荷载脉冲模型。该简化的冲击荷载模型，可为开展薄膜型液化天然气储液舱结构动响应分析提供荷载参考。

1晃荡模型实验

以薄膜型液化天然气储液舱的纵向矩形截面为研究对象，进行λ=1∶40的几何缩比，得到模型实验所用的二维矩形液舱，其内壁尺寸：长(L)为946 mm, 高(H)为670 mm, 宽(B)为118 mm,L/B≈8，适当的长宽比既可以保证舱内全局流场的二维特性，又可以忽略沿着液舱宽度方向上产生的边界层厚度对实验测试结果的影响[17-19]。矩形液舱主尺度及坐标轴定义(见图1)。

图1　矩形舱主尺度，俯视图和正视图(mm) Fig.1 Rectangular tank dimensions, top view and front view(mm)

实验选取载液率h/H=0.85 (h为载液高度，h=569.5 mm)开展研究。该载液率下，舱内液体主要冲击矩形舱顶部两端，所以监测冲击荷载的压力传感器集中布置于液舱顶部左侧边缘处。实验共采用8个针孔型压阻式传感器，测量误差为5.26‰[19]，传感器具体布点位置及编号(见图2)。

图2　液舱顶部压力传感器布置(mm) Fig.2 Pressure sensors map, top view(mm)

由于冲击荷载上升和持续时间一般为毫秒量级[5-6]，选择适当的数据采样频率对于压力传感器有效捕捉冲击荷载峰值非常关键[20]，本文的实验数据采样频率为20 kHz。

大吨位六自由度运动平台(见图3)，最大负载12 t，电动平台，可模拟船体六个自由度的规则和不规则运动。平台在六个自由度的最大位移(见表1)，其运动精度平动为±1 mm，转动为±0.1°。

表1　平台运动最大位移

图3　六自由度运动平台 Fig.3 Hexapod test rig

不规则的外激激励最能反映船体的真实运动，通过Froude相似将LNG船舶运动的时程曲线转化为实验平台运动的不规则激励时程，共开展三种不同的实验工况，C1, C2和C3。本文定义六自由度运动平台沿液舱x，y，z轴方向的平动分别为横荡，纵荡和垂荡；绕液舱x，y，z轴方向的转动分别为纵摇，横摇和艏摇，其中工况C1的平台激励为不规则横荡激励，C2为不规则横荡，横摇和垂荡的耦合激励，C3为不规则横摇激励。每个工况重复实验6次，每次持续30 min，以3 h的完整数据进行后期分析。具体的实验工况参数(见表2)。

表2　实验工况

2数据处理方法

图4给出了工况C2，第一组实验的一段时间范围(320～420 s)，2#传感器典型的压力时程曲线，记录了该测点位置在实验过程中受到的冲击荷载变化。一组较长时间(Long duration)的晃荡模型实验，其压力时程曲线是由大量的冲击事件(Sloshing event)组成，每一个冲击事件中，冲击荷载都是由最小值经过几毫秒或几十毫秒上升到最大值，之后又经过几毫秒或几十毫秒下降到最小值。对于储舱结构设计荷载，只有较大的荷载峰值才具有实际意义，设定阈值(Threshold)为5 kPa，时间间隔(Time interval)为100 ms，即在100 ms的范围内大于阈值5 kPa的冲击荷载峰值才被定义为有效冲击，即发生一次冲击事件，而每分钟发生的冲击事件个数定义为冲击率(Event Rate, ER)。

图4　压力时程曲线 Fig.4 Pressure time history

以图4的一个典型冲击事件为研究对象(见图5)，定义冲击荷载值从0.5×荷载峰值(0.5×Pmax)上升到荷载峰值(Pmax)的时间间隔为冲击荷载上升时间的一半0.5×上升时间(0.5×Trise)，同理可知由荷载峰值Pmax下降到0.5×Pmax的时间间隔为冲击荷载下降时间的一半0.5×下降时间(0.5×Tdecay)，即有公式：

Trise=2(tPmax-t(0.5Pmax)up-crossing )

(1)

Tdecay=2(t(0.5Pmax)down-crossing -tPmax)

(2)

则对于一个典型的冲击荷载，其冲击持续时间有公式：

Tduration=Trise+Tdecay

(3)

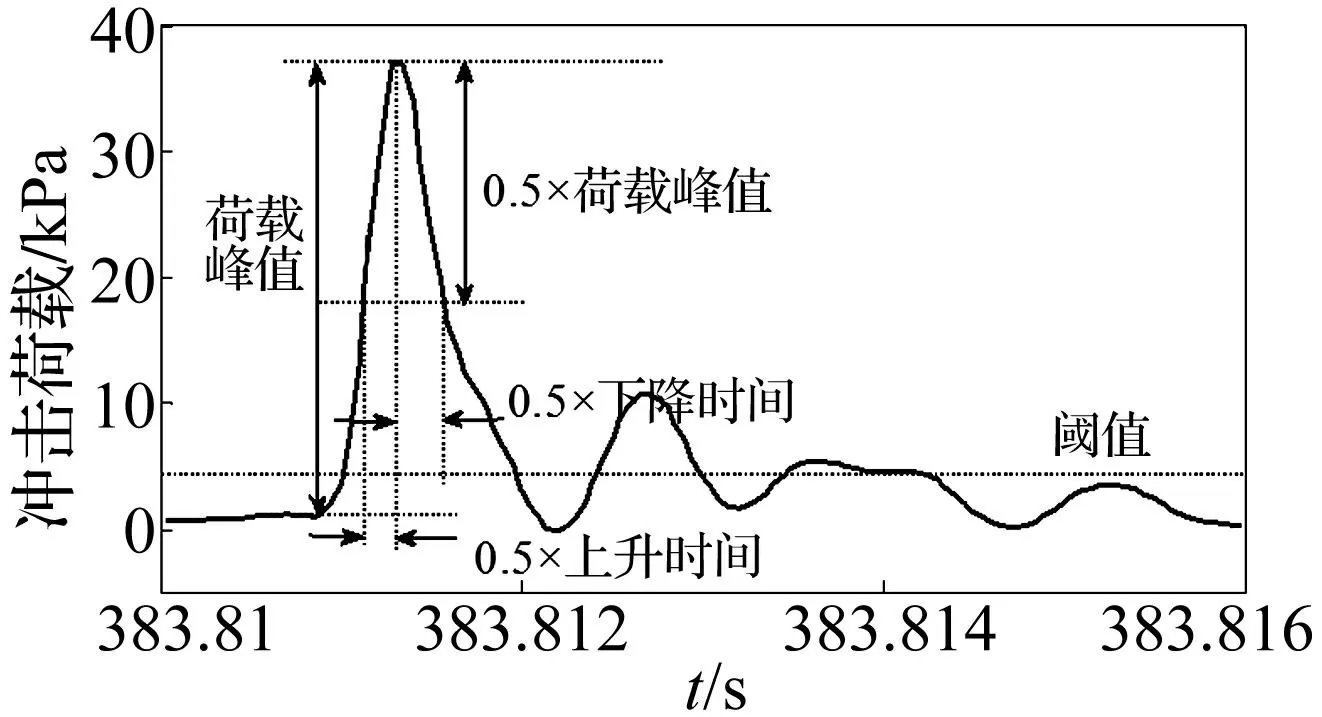
图5　冲击荷载上升时间和下降时间 Fig.5 Rise time and decay time of impact pressure

冲击荷载的上升和持续时间一般都是毫秒量级，图5所示的Trise就小于1ms。对于一个典型的冲击事件，冲击荷载从开始到结束的过程一般可简化为一个三角脉冲，而对于完整晃荡模型实验中大量的冲击事件，其每一个冲击事件具有不同的荷载上升时间和持续时间，所以其简化后的每一个三角脉冲的偏斜度 (Skewness)也是不尽相同的，定义冲击荷载三角脉冲的偏斜度公式：

Skewness=2Trise/Tduration

(4)

晃荡模型实验测得的冲击荷载，其偏斜度的值在0～2之间变化。偏斜度不同的值表征了储舱内流体冲击壁面过程及冲击荷载脉冲形状的差异。本文结合实验中观测到的冲击过程中伴随的复杂物理现象，对偏斜度进行了解释：若偏斜度<1(见图6(a))，则表明冲击荷载具有较小的上升时间，表现为典型的不可压缩流体的水动力冲击；当偏斜度≈1时(见图6(b))，冲击荷载三角脉冲接近于对称形式，表现为在冲击过程中，气体被截留，液体与侧壁或舱顶形成气体空隙, 图中当液体以速度U2冲击液舱顶部时，在液舱侧壁与顶部的拐角处发生了气体被截留的现象；偏斜度>1的冲击荷载(见图6(c))，则具有较长的荷载上升时间，且冲击过程中伴随着大量的气泡。

图6　晃荡冲击荷载脉冲形式 Fig.6 Triangular impulse for impact pressure

3结果分析与讨论

首先计算三种工况下，每一个测点位置六组实验所测冲击荷载的冲击率平均值。分别对每个工况下冲击率平均值较大的三个测点位置进行冲击荷载上升时间，持续时间和脉冲偏斜度的分析研究。

3.1冲击荷载的冲击率

图7分别给出了C1, C2, C3三种工况下，8个压力传感器六组实验测得冲击荷载的冲击率平均值(Mean ER)及其标准差(standard deviation)。可以得到：①三种工况下，ER平均值均大于10，表明所有传感器在一分钟时间内，其受到冲击次数的平均值都在10次以上；②对于同一个传感器在三种工况下的ER平均值，工况C2的冲击次数更多，即三自由度耦合激励下的晃荡冲击事件发生次数较单自由度激励下的更多；③三种工况下，Mean ER较大的三个值均发生在1#，2#和4#压力传感器，这三个传感器都位于液舱顶部靠近侧壁的一列，由此可知该列传感器在液舱晃荡过程中受到的冲击次数较多。

同时冲击峰值的响应周期(Response period)等于冲击率的倒数，即1/ER，该值表示冲击事件发生的平均周期。

图7　冲击率 (ER)平均值和标准差 Fig.7 Mean ER with standard deviation

3.2冲击荷载的上升时间和偏斜度

基于晃荡冲击荷载的储舱结构设计不仅要考虑荷载峰值的大小及其概率分布，还要充分分析影响储舱舱壁结构动响应的其他荷载参数，包括冲击荷载的上升和持续时间以及偏斜度等。

冲击荷载上升时间Trise和持续时间Tduration的值一般只有几毫秒到几十毫秒，液体对舱壁舱壁的冲击是一种瞬态冲击过程，伴随着瞬间的，强烈的能量释放或者转化。当冲击造成局部应力达到舱壁结构的许用应力时可能就会对结构造成破坏，从而影响液舱的正常工作。因此，储舱结构设计时，其结构自振频率应尽可能避开冲击荷载的上升时间和持续时间。

通过晃荡模型实验可以得到大量具有不同上升和持续时间的冲击荷载，将这些荷载作用到储舱结构上进行有限元分析，得到结构动响应(Dynamicresponse，DR)和静响应(Staticresponse，SR)，定义DR/SR的值为动力放大因子(Dynamicamplificationfactor，DAF)，并定义Pmax×DAF的值为评估储舱结构安全的等效荷载，即结构设计荷载。荷载冲击的快慢将会影响动力放大因子的值，进而影响储舱结构设计荷载值。图8为英国劳氏船级社规范中，关于储舱结构设计时，动力放大因子与晃荡冲击荷载上升时间的关系曲线[3]，即DAF随Trise的变化趋势。当冲击荷载上升时间小于结构的自振周期时，其动力放大因子DAF较小，如图8中“a”段所示，随着上升时间逐渐接近于结构的自振周期，DAF增大并达到最大值，此时储舱舱壁具有较大的结构响应，如图8中“b”段所示，随着上升时间的继续增大且远离于结构的自振周期，则DAF也随之减小，如图8中“c”段所示。虽然有限元分析时建模方法的不同可能会产生储舱舱壁结构的自振周期略有不同，进而会导致结构发生较大结构响应的上升范围有所不同。但是对于原型液舱而言，其值一般在5～10 ms的范围内，而对于实验为λ=1∶40的模型液舱，根据Froude相似可以确定其时间范围在0.79～1.58 ms。因此，上升时间在这个范围内且峰值较大的冲击荷载在储舱结构设计时要重点关注。

图8　动力放大因子(英国劳氏船级社) Fig.8 Dynamic amplification factor (Lloyd’s Register)

图9、图10和图11 (a)图分别给出了三种工况下，1#，2#和4#传感器测得的每一个冲击荷载所对应的的上升时间Trise，得到以下结论：①对于峰值Pmax<50kPa的冲击荷载，其上升时间分布范围较广，从几毫秒到几十毫秒，其中某些荷载峰值(Pmax<10kPa)的上升时间可>20ms；②对于峰值Pmax>50kPa的冲击荷载，具有较小的荷载上升时间，局部放大图9、图10和图11(a)图中冲击压力为50～60kPa对应的冲击上升时间，即(a)中虚线框所示的范围，放大结果分别详见图9、图10和图11(b)所示。图中工况2和3中存在上升时间在0.79～1.58ms范围内的晃荡冲击荷载，处于能够使储舱舱壁产生较大结构响应的时间范围内，在储舱结构设计时要重点考虑这些峰值大，冲击快，易使舱壁结构发生共振，导致较大结构响应的冲击荷载；③三种工况下，冲击荷载上升时间的分布规律基本一致，表明冲击荷载上升时间具有一定的属性，其峰值较大的冲击荷载往往冲击较快，而峰值较小的冲击荷载冲击较慢。

(a)荷载峰值与上升时间的关系(b)载荷峰值在50～60kPa对应的冲击上升时间的放大图(a)荷载峰值与上升时间的关系(b)载荷峰值在50～60kPa对应的冲击上升时间的放大图(a)荷载峰值与上升时间的关系(b)载荷峰值在50-60kPa对应的冲击上升时间的放大图图9 工况C1,冲击荷载的上升时间Fig.9RisetimeofimpactloadsofC1图10 工况C2,冲击荷载的上升时间Fig.10RisetimeofimpactloadsofC2图11 工况C3,冲击荷载的上升时间Fig.11RisetimeofimpactloadsofC3

由式(4)计算三种工况下，峰值Pmax大于50kPa的冲击荷载三角脉冲的偏斜度Skewness，如图12所示,得到以下结论：①冲击荷载(Pmax>50kPa)脉冲的偏斜度的值大部分在0.5～1.5之间变化，没有出现冲击荷载下降时间Tdecay远大于上升时间Trise或者Trise远大于Tdecay的情况；②冲击荷载(Pmax>50kPa)脉冲的偏斜度的值集中于1附近，由图6可知其冲击过程发生气体被截留现象，表明较大的冲击荷载往往是液体和气体共同作用的结果；③由图9，图10和图11可知，冲击荷载(Pmax>50kPa)的上升时间集中在1ms左右，然而图12显示其偏斜度的分布范围较广，表明即使是具有相同上升时间的冲击荷载，其偏斜度的值也不尽相同，而具有不同偏斜度值的冲击荷载也是储舱舱壁结构设计的重要考量。

图12　冲击荷载三角脉冲的偏斜度 Fig.12 Skewness for impact pressure triangular impulse

3.3储舱结构设计荷载形式

确定包含有峰值大小，上升和持续时间以及脉冲偏斜度的晃荡冲击荷载是储舱舱壁结构设计与分析的关键内容。为此综合三种工况下，即图9、图10和图11中所有峰值Pmax>50kPa且上升时间范围为0.79～1.58ms的冲击荷载，计算其脉冲偏斜度小于、约等于和大于1三种情况下的晃荡冲击荷载简化模型(见图13)。

图13中冲击荷载的三种简化模型的上升时间(竖直虚线对应横坐标)均位于使结构产生较大响应的时间范围内，该简化形式可为薄膜型液化天然气储舱舱壁结构设计有限元分析提供荷载参考。

图13　设计荷载的简化模型 Fig.13 Idealized triangular pressure model of design loading

4结论

为了确定储舱舱壁结构设计荷载信息，在大吨位六自由度运动平台开展了长期的不规则激励下的二维矩形舱晃荡模型实验。通过统计学的方法分别研究了晃荡冲击荷载峰值、其上升和持续时间以及偏斜度等储舱结构设计需要的荷载参数，得到以下主要结论：

(1)高载液工况下(h/H=0.85)，晃荡冲击荷载主要冲击储舱顶部边缘，且耦合激励(横荡，横摇和垂荡)比单自由度激励的冲击更为剧烈。因此，针对长期的耦合不规则激励实验研究是非常有必要的；

(2)由于液体和气体的相互作用，导致晃荡冲击荷载具有较大的幅值，且冲击上升时间较短；

(3)基于实验结果，给出了晃荡冲击荷载大于50 kPa且上升时间接近结构最高阶固有周期的三角脉冲简化模型，可为储舱结构设计有限元分析提供荷载参考。

致谢

作者衷心感谢对于文本提出宝贵意见和建议的审稿人员和编辑们。

参考文献

[1]Veritas D N. Sloshing analysis of LNG membrane tanks[S]. Classification notes, Oslo, Norway, 2006.

[2]American Bureau of Shipping. Strength assessment of membrane-type LNG containment systems under sloshing loads[S]. Guidance Notes,2009.

[3]Lloyd’s Register. Sloshing assessment guidance document for membrane tank LNG operations[S]. Guidance Notes Version 2.0. 2009.

[4]Faltinsen O M, Timokha A N. Sloshing[M]. Cambridge:Cambridge University Press, 2009.

[5]王德禹. 液化天然气船液舱的晃荡[J]. 计算机辅助工程, 2010, 19(3): 1-4.

WANG De-yu.Sloshing in LNG carriers tanks[J]. Computer Aided Engineering, 2010, 19(3): 1-4.

[6]王德禹, 金咸定. 液舱流体晃荡的模型试验[J]. 上海交通大学学报, 1998, 32(11): 114-117.

WANG De-yu, JIN Xian-ding. On model experiment of sloshing in tanks[J]. Journal of Shanghai Jiaotong University, 1998, 32(11): 114-117.

[7]卫志军, 岳前进, 阮诗伦, 等. 矩形液舱晃荡冲击载荷的试验机理研究[J]. 船舶力学, 2012, 16(8): 885-892.

WEI Zhi-yun, YUE Qian-jin, RUAN Shi-lun, et al. An experimental investigation of liquid sloshing impact load on a rectangular tank [J]. Ship Mechanics, 2012, 16(8): 885-892.

[8]朱仁庆.液体晃荡及其与结构的相互作用 [D]. 无锡: 中国船舶科学研究中心, 2002.

[9]朱仁庆, 吴有生. 船舶液体晃荡动力学的研究方法及进展[J]. 华东船舶工业学院学报, 1999, 13(1): 45-50.

ZHU Ren-qing, WU You-sheng. Study and advance of liquid sloshing dynamics of ship[J]. Journal of East China Shipbuilding Institute, 1999, 13(1): 45-50.

[10]刘泽民. 关于船舱中液体晃荡问题[J]. 哈尔滨船舶工程学院学报, 1992, 13(3): 241-249.

LIU Ze-min. On liquid sloshing in partially filled tanks[J]. Journal of Harbin Shipbuilding Engineering Institute, 1992, 13(3): 241-249.

[11]Pillon B, Marhem M, Leclère G, et al. Numerical approach for structural assessment of LNG containment systems[C]//Proceedings of 19th International Offshore and Polar Engineering Conference, June 21-26, Osaka, Japan. 2009.

[12]Dobashi H, Usami A. Dynamic amplification factor of NO96 insulation structures of membrane system[C]//The Twenty-second International Offshore and Polar Engineering Conference. International Society of Offshore and Polar Engineers, 2012.

[13]Yoo M J, Lee S J, Kim S C, et al. Characteristics of dynamic response of mark Ⅲ LNG containment subjected to idealized triangular sloshing impact[C]//The Twenty-first International Offshore and Polar Engineering Conference. International Society of Offshore and Polar Engineers, 2011.

[14]Graczyk M, Moan T, Rognebakke O. Probabilistic analysis of characteristic pressure for LNG tanks[J]. Journal of Offshore Mechanics and Arctic Engineering, 2006, 128(2): 133-144.

[15]Kim Y, Kim S Y, Yoo W J. Statistical evaluation of local impact pressures in sloshing[C]//Proceedings of the 20th international offshore and polar engineering conference, ISOPE, Beijing, China. 2010.

[16]Graczyk M, Moan T. A probabilistic assessment of design sloshing pressure time histories in LNG tanks[J]. Ocean Engineering, 2008, 35(8): 834-855.

[17]Loysel T, Chollet S, Gervaise E, et al. Results of the first sloshing model test benchmark[C]//Proceedings of the 22th International Offshore and Polar Engineering Conference. 2012: 17-22.

[18]Faltinsen O M, Firoozkoohi R, Timokha A N. Steady-state liquid sloshing in a rectangular tank with a slat-type screen in the middle: Quasilinear modal analysis and experiments[J]. Physics of Fluids, 2011, 23(4): 042101.

[19]卫志军, 岳前进, 张文首, 等. 大尺度储舱内流体晃荡砰击压力的测量方法研究[J]. 中国科学：物理 力学 天文学, 2014,44:746-758.

WEI Zhe-jun, YUE Qian-jin, ZHANG Wen-shou, et, al. Experimental investigation of violent slamming pressure in large-scaled tank[J]. Sci Sin-Phys, Mech Astron, 2014, 44:746-758.

[20]Repalle N, Truong T, Thiagarajan K, et al. The effect of sampling rate on the statistics of impact pressure[C]//ASME Conf Proc. 2010, 49095: 565-572.