基于计算机视觉的位移测试方法研究与实现

第一作者陈苏男，博士，助理员，1986年生

通信作者陈国兴男，教授，1963年生

基于计算机视觉的位移测试方法研究与实现

陈苏1,2，陈国兴2，韩晓健2，戚承志3，杜修力4

(1.中国地震局地球物理研究所，北京100081; 2. 江苏省土木工程防震技术研究中心，南京210009；3.北京建筑大学土木与交通工程学院，北京100044； 4.北京工业大学建筑工程学院，北京100022)

摘要：针对Hough变换、最优圆拟合两种圆检测算法进行了圆检测效果、算法应用范围及计算效率的对比分析；研发了基于圆检测算法的非接触性动态位移测试方法并应用于大型振动台实验。结果表明：Hough变换圆检测及最优圆拟合圆检测均具有较好的圆参数检测效果。Hough变换圆检测方法更适用于测试背景简单且需单次识别多个标靶圆的工况；最优圆拟合圆检测方法更适用于测试背景复杂的工况。应用非接触性位移测试方法于大型振动台试验中，测试了模型地基土的位移反应。应用基于机器视觉技术的位移测试方法可以有效解决复杂工况下的位移测试问题。

关键词：Hough变换圆检测；最优圆拟合圆检测；非接触性位移测试方法；振动台试验

基金项目：国家自然科学基金重大研究计划项目(90715018);北京市自然科学

收稿日期：2014-02-26修改稿收到日期：2014-07-22

中图分类号:TU47文献标志码：A

基金项目：国家科技支撑计划(2011BAK12B07)；国家自然科学基金(51278236)

Development of vision-based displacement test method

CHENSu1,2,CHENGuo-xing2,HANXiao-jian2,QICheng-zhi3,DUXiu-li4(1. Institute of Geophysics, China earthquake administration, Beijing 10081, China;2. Civil Engineering&Earthquake Disaster Prevention Center of Jiangsu Province, Nanjing 210009, China;3. School of Civil and Transportation Engineering, Beijing University of Civil Engineering and Architecture, Beijing 100044, China;4. College of Architecture and Civil Engineering, Beijing University of Technology, Beijing 100022, China)

Abstract:The circle detection effect, algorithm application range and calculation efficiency of different circle detection algorithms were analysed comparatively. Base on the circle detection algorithms, a vision-based dynamic displacement test method was developed and applied to large-scale shaking table tests. The results show that: both Hough transform circle detection algorithm and optimal fitting circle detection algorithm have good performance in circle parameters detection. The Hough transform circle detection algorithm is more suitable for testing under such operation conditions in which the test background is simple or with the need of identifying multiple target circles at once. The optimal fitting circle detection method is more suitable for testing under such operation conditions in which the test background is complex. By applying the vision-based displacement testing method to large-scale shaking table tests, the deformation of a model of soil foundation was tested. The method proposed can effectively solve the problem of displacement testing in complex test conditions.

Key words:hough transform circle detection; optimal circle fitting circle detection; non-contact displacement test method; shaking table test

近年来，计算机视觉研究已成为热点，特别是在交叉学科中得到了长足的发展，例如：生物特征识别、医学影像处理、工业制造、智能交通目标识别、安全防护等[1-6]。通过计算机视觉对目标物识别具有非接触、高精度、全局化等“先天优势”。但是，大部分计算机视觉研发人员缺少应用的专业背景，而有工程需要的工程师缺少专业交叉及程序编写能力，使得智能化测试技术不能在工程中得到广泛普及。因此，本文首先对比分析了不同圆检测识别算法圆检测效果、计算效率及应用范围等算法计算参数；在此基础上研发了位移测试方法，并将此方法应用于大型振动台模型试验的位移测试中。本文的研究工作可以有效解决土木工程(大跨桥梁、高耸结构物、基坑等)、机械工程领域等传感器不便布设环境下的位移测试问题。

1非接触性位移测试方法研发思路

非接触性动态位移测试方法研发的基本思路：采用高速相机采集动态视频并对其进行分帧，并对分帧后连续静态图像进行预处理，包括：图像降噪与灰度处理、校正RGB(表示红、绿、蓝)三原色的色彩比例等。通过调用Matlab软件自带的边缘检测算法模块对图像进行边缘检测；在此基础上，外挂圆检测模块，识别出图像中的标靶圆，进而获取圆心坐标及半径，按连续静态图片的排列顺序依次存储检测到的标靶圆圆心坐标，即可获得图像空间中标靶圆圆心的水平、竖直位移时程曲线；再通过标定图像像素与实际物像坐标的关系，即可得到物像坐标下的真实位移。非接触性位移测试方法流程见图1。本文分别采用了Hough变换圆检测算法、最优圆拟合算法的两种圆检测方法进行动态位移测试方法的研发，并进行了对比分析。

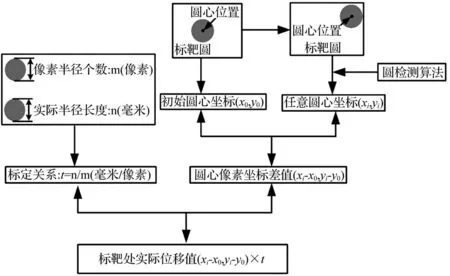
图1　非接触性位移测试方法研发流程图 Fig.1 Program development chart of non-contact displacement test method

2圆检测算法简介

2.1Hough变换圆检测基本原理

Hough变换[7]的基本原理：提取图像中直线、圆、椭圆甚至是任意形状的边缘，实现从图像空间到参数空间的映射(见图2)。Hough变换圆检测的基本原理为：图像空间中圆心坐标为O1(a,b)、半径为r的圆，可采用式(1)表征：

(X-a)2+(Y-b)2=r2

(1)

将图像空间[X,Y]T中的标靶圆中任意点变换到参数空间[a,b,r]T，可以用式(2)表征：

(2)

式中：x和y为实际图像空间中点的坐标，a，b和r为其对应在参数空间中的坐标，θ为检索角，极坐标参数r，θ可以表征图像空间圆内任意点。通过式(2)，圆所在的图像空间中的点可以映射到参数空间[a,b,r]T中,表现为参数空间中的三维锥面。由图2(b)可知：图像空间中圆的圆周边缘点由于被圆心及半径约束，对应在参数空间中的三维锥面必交于一点，共同交点坐标含义为图像空间中圆的圆心坐标(a,b)及半径r的长度值。

图2　Hough变换圆检测的基本原理 Fig.2 Basic principle of Hough transform round detection

Hough变换圆检测算法需要对参数空间离散化，并对圆边缘点在三维参数空间内逐点比较，记录。算法的渐近时间复杂度为：O(n4)。

2.2最优圆拟合圆检测基本原理

最优圆拟合算法基于最小二乘法进行圆拟合，其基本原理为：采用标靶圆边缘点拟合所得的圆逼近标靶圆的轮廓，采用标靶圆边缘点拟合所得的圆与标靶圆边缘点组成的圆之间的残差采用式(3)表征：

ξi=(Xi-a)2+(Yi-b)2-r2

(3)

残差平方和为：

式中：edge为标靶圆边缘点集合；(Xi,Yi)为图像标靶圆边缘点坐标。

残差平方和最小的数学表达可由式(5)表征：

(5)

式(5)可化简为：

(6)

据此，可得关于a、b的非线性方程组：

(7)

因此，a,b和r的表达式可由式(8)表征：

(8)

式(8)仅需采用标靶圆边缘点进行一次运算，即可获取标靶圆参数(圆心坐标及半径)，算法的渐近时间复杂度为：O(n)。

2.3标靶圆检测效果

为验证不同圆检测算法的准确性，笔者建立了如图3(a)，图3(b)所示的由单圆及多圆组成的图像。采用Matlab软件自带的Canny算法模块[8]检测图像边缘。单圆圆心检测结果见图3(c)。由图可知：采用Hough变换圆检测得到的圆心坐标(237.29，199.83)与采用最优圆拟合算法得到的圆心坐标(237.70，200.28)基本一致，两种算法均可以较好的检测到标靶圆的圆心位置。采用Hough变换圆检测算法计算得到的标靶圆半径为：196.85(像素)，采用最优圆拟合算法计算得到的标靶圆半径为：191.16(像素)，两者存在较小误差，这是由于：采用Hough变换进行圆检测，仅采用边缘点坐标进行计算，不考虑边缘是否是最优圆；而采用最优圆拟合算法计算时，采用标靶圆边缘点拟合所得的圆逼近标靶圆边缘，得到最优解。

图3　不同圆检测算法的的检测效果 Fig.3 Detection effect by different circle detection arithmetics

采用最优圆拟合算法计算圆参数具备计算参数少，识别精度高的优点，但也存在“天生”的缺陷：在图像中存在多个标靶圆时，需要逐次进行单个圆参数的识别。如图3(d)所示的图像，采用Hough变换进行圆参数识别时，可以单次识别出图中的9个单圆，若采用最优圆拟合算法，则需要将图像分为9个区域(每圆一个区域)，分次进行圆参数的计算，计算效率不够经济。因此，实际进行位移测试时，若需单次识别多个标靶圆，建议采用基于Hough变换的非接触性位移测试方法，但需要用户自行对Hough变换三个重要参数进行反复试算：①标靶圆半径上、下界；②半径、角度的检测步长；③Hough变换阈值，取(0,1)区间。若工况背景噪声较大工况下，建议采用基于最优圆拟合算法的非接触性位移测试方法。

3非接触性位移测试方法验证及应用

3.1不同算法计算效率对比

本文验证两种圆检测算法间的识别精度关系及计算效率。采用ABAQUS建立圆形解析刚体，并在刚体参考点处施加0.5 Hz；1 Hz；4 Hz的水平向正弦位移，输入位移及采用不同圆检测算法测得的位移归一化结果见图4，由图4可知：两种方法测得的位移形态一致，幅值相同。作者采用二元定距变量的相关分析方法对两种测试方法测得的位移进行相关性评价。采用Pearson相关系数[9]作为评价指标，其计算公式可用式(9)表征：

(9)

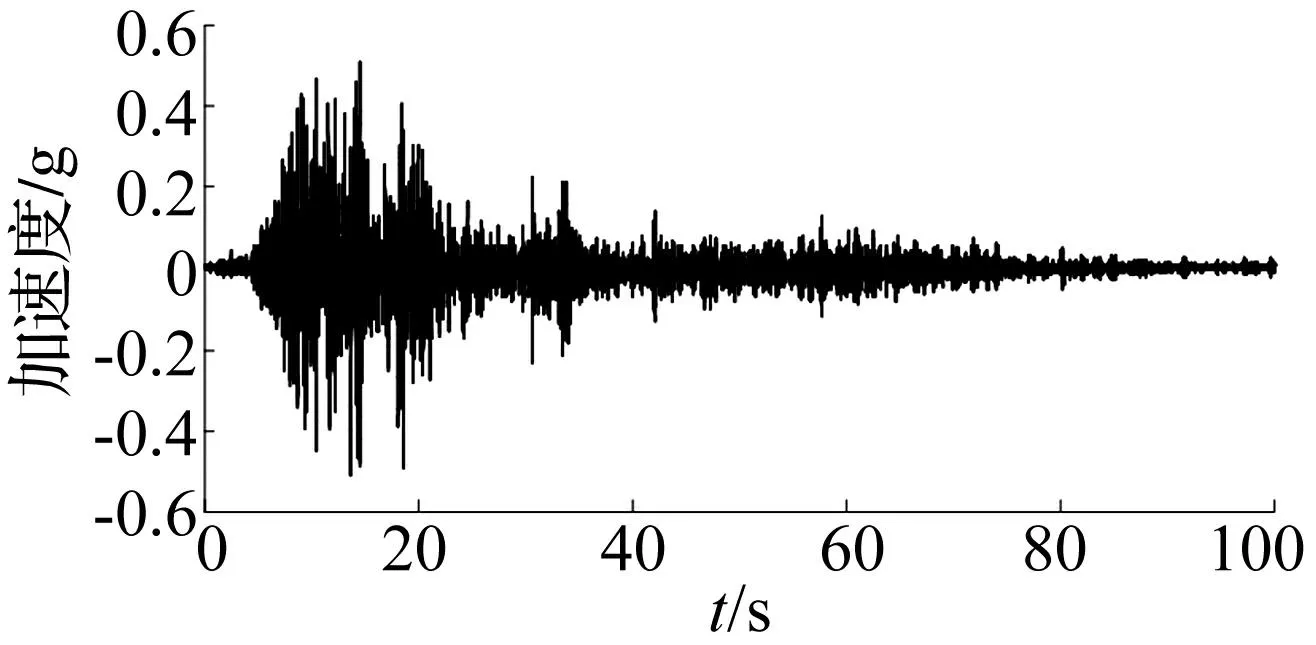
式中：若0

采用两种圆检测方法研发的非接触性动态位移测试方法的计算时间见图5。由图5(a)可知：基于Hough变换圆检测算法研发的动态位移测试方法的计算时间与图片中标靶圆个数无显著联系。因此，若工况中需要测试的位移点位较多时，选取此方法。由图5(b)和图5(c)可知：若图片中仅存单圆，达到相同精度时，基于最优圆拟合算法研发的动态位移测试方法的计算时间显著低于基于Hough变换圆检测研发的动态位移测试方法的计算时间，这与算法的渐近时间复杂度相关。随着图片中标靶圆数量的增加，基于最优圆拟合算法研发的动态位移测试方法的计算时间将大幅提高，这是由于标靶圆需单个逐次进行圆参数的识别。

图4　采用不同动态位移测试方法测得的位移 Fig.4 The displacement obtained by different non-contact displacement test method

图5　不同测试方法的计算时间对比 Fig.5 The elapsed time of different non-contact displacement test method

3.2振动台实验位移测试中的应用

验证试验在南京工业大学土木工程与防灾减灾重点实验室开展。验证试验体系见图6。振动台分别输入1 Hz，3 Hz简谐振动及复杂频率组成的地震动，以验证不同输入条件下，研发方法的准确性。

图6　验证体系 Fig.6 The typical picture of experimental condition

由图6可知：不同激励下，研发的测试方法与激光位移计测试结果位移形态一致。以百分误差(Percent Error)及均方根误差(RMSE)作为非接触性位移测试结果与位移计测试结果相似度的定量判别指标[10]。不同实验条件下，以激光位移计测试所得位移结果作为标准，各工况下非接触性位移测试方法识别所得位移与位移计测试位移的误差分析见表1。由表1可知：采用非接触性位移测试方法测得的台面位移与位移计测得的位移的百分误差均小于1.8%；均方根误差均小于1 mm，验证了自行研发的非接触性动态位移测试方法对于不同测试条件下均具有较好的测试效果。

图7　正弦波作用下位移对比 Fig.7 Displacement response comparing the vision-based test method and actuator LVDT feedback under 1 Hz and 3 Hz

(10)

(11)

式中：Vi表示非接触性位移测试结果；Mi表示激光位移计测试结果。

表1

3.3模型地基土侧向变形大型振动台实验

目前开展的大型振动台试验中，模型地基土位移测试的技术难点在于模型地基土安装在模型土箱中，位移传感器安装困难。笔者将非接触性动态位移测试方法应用于大型振动台试验中，并测试了模型地基土的水平、竖直位移。现有研究表明：叠层剪切型模型土箱可以有效减少对土体剪切变形的约束；箱体各层方刚管的水平位移近似代表了所在土层的水平位移[11]。本次试验共布设位移测试标靶圆8个，模型地基位移测试标靶布置见图6。由于实验要求测试精度高，本实验采用基于最优圆拟合算法的非接触性动态位移测试方案。不同地震动作用下，模型地基地表(模型土箱顶部测点PltA)水平位移、竖直位移见图7～图8(SF-1，SF-2，SP-1，SP-2，TA-1，TA-2分别代表振动台输入0.1 g什邡地震动，0.3 g什邡地震动；0.1 g松潘地震动，0.3 g松潘地震动；0.1 gTaft地震动，0.1 gTaft地震动)。

图8　台面输入地震动 Fig.8 Ground motion acceleration time histories and Fourier spectra on the shaking table surface

图9　地震动作用下位移对比 Fig.9 Displacement response comparing the vision-based test method and actuator LVDT feedback

由图可知：不同地震动作用下，模型土箱仅发生微小的竖向振动，最大竖向位移均小于0.6 mm，可以近似认为在水平向地震动过程中，模型土箱只发生水平向振动。该结论验证了模型土箱导向装置(直线导轨-滚珠体系)足够光滑，水平向运动无约束，竖向约束好。不同地震动作用时，模型地基测点PltA～PltG左摆、右摆的水平位移峰值见图9。发现模型地基左摆、右摆的位移出现了不同程度的不对称现象，这与输入地震动位移的正、负峰值不对称性相关。

模型地基的水平位移反应与输入地震动的频谱特性有关，远场松潘波作用引起的模型地基水平位移峰值大于近场什邡波作用引起的地基水平位移峰值。这表明:输入地震动的峰值加速度相同时，模型地基的水平位移反应对低频成分比较发育的地震动更为强烈。模型地基左、右摆过程中，呈现出模型结构顶部土层(测点PltB)的水平位移大于模型结构底部土层(测点PltD)的现象(见图10～图13)。

图10　模型土箱位移标靶测点布置(单位：mm) Fig.10 Arrangement of displacement test target sensors embedded in the model foundation(unit：mm)

图11　0.1 g地震动作用下模型土箱PltA测点水平、竖直位移反应(单位：mm) Fig.11 Horizontal and vertical displacement responses of measuring point PltA under 0.1 g ground motion(unit:mm)

图12　0.3 g地震动作用下模型土箱PltA测点水平、竖直位移反应(单位：mm) Fig.12 Horizontal and vertical displacement responses of measuring point PltA under 0.3 g ground motion(unit:mm)

图13　模型地基水平位移响应 Fig.13 Arrangement of displacement test target sensors embedded in the model foundation

4结论

本文对不同圆检测算法的圆检测效果、应用范围及计算效率进行了验证分析，研发了非接触性动态位移测试方法，应用此方法于大型振动台试验中，得到如下结论：

Hough变换圆检测及最优圆拟合圆检测均具有较好的圆参数检测效果。若外部条件简单且需单次识别多个标靶圆，建议采用Hough变换圆检测方法；若工况条件复杂，建议采用最优圆拟合圆检测方法。研发了非接触性动态位移测试方法并应用于大型振动台试验中，测试了可液化非自由场模型地基土的位移反应。

参考文献

[1]Dhiman Karmakar C A. Generation of new points for training set and feature-level fusion in multimodal biometric identification[J]. Machine Vision and Applications, 2014(25): 477-487.

[2]Dickinson A W L, Abolmaesumi P, Gobbi D G, et al. SimITK: Visual Programming of the ITK Image-Processing Library within Simulink[J]. J Digit Imaging,2014,32(12):220-230.

[3]贾慧星，章毓晋. 车辆辅助驾驶系统中基于计算机视觉的行人检测研究综述[J].自动化学报,2007,33(1): 84-90.

JIA Hui-Xing, ZHANG Yu-Jin, et al. A survey of computer vision based pedestrian detection for driver assistance systems [J]. Acta Automatical Sinica,2007,33(1): 84-90.

[4]杨会臣，贾金生，王海波. 高速摄影测量在振动台动力模型试验中的应用[J].水电能源科学,2012(1):153-155.

YANG Hui-chen, JIA Jin-sheng, WANG Hai-bo. Application of high speed photogrammetry to vibrating platform dynamic model test [J]. Water Resources and Power,2012(1): 153-155.

[5]任伟中，寇新建，凌浩美. 数字化近景摄影测量在模型试验变形测量中的应用[J].岩石力学与工程学报,2004(3): 436-440.

REN Wei-zhong, KOU Xing-jian, LING Hao-mei. Application of digital close-range photogrammetry in deformation measurement of model test [J]. Chinese Journal of Rock Mechanics and Engineering,2004(3): 436-440.

[6]陈佳娟, 纪寿文, 李娟，等. 采用计算机视觉进行棉花虫害程度的自动测定[J].农业工程学报,2001,17(2): 157-160.

CHEN Jia-juan, JI Shou-wen LI Juan, et al. Automatic measurement of danger degree of cotton insect pests using computer vision[J]. Transactions of the CSAE,2001,17(2): 157-160.

[7]Hough P V C. Methods and means for recognizing complex patterns: US, 3069654 [P]. [1962-12-18].

[8]Deriche R. Using Canny’s criteria to derive a recursively implemented optimal edge detector[J]. International Journal of Computer Vision, 1987:167-187.

[9]Cohen J. Statistical power analysis for the behavioral sciences[M]. Lawrence Erlbaum, New Jersey, 1988.

[10]Hyndmana R J, Koehlerb A B. Another look at measures of forecast accuracy[J]. Int. J. Forecast. 2006, 22(4):679-688.

[11]陈国兴, 王志华, 左熹, 等. 振动台试验叠层剪切型土箱的研制[J].岩土工程学报, 2010, 32(1): 89-97.

CHEN Guo-xing, WANG Zhi-hua, ZUO Xi, et al. Development of laminar shear soil container for shaking table tests[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(1): 89-97.