半参数模型在平面坐标转换中的应用

赵富燕,孙李城,杨兆臣

(山东科技大学测绘科学与工程学院,山东 青岛 266590)

半参数模型在平面坐标转换中的应用

赵富燕,孙李城,杨兆臣

(山东科技大学测绘科学与工程学院,山东 青岛 266590)

摘要：坐标转换在测绘领域一直起着至关重要的作用,而模型的选取又直接制约着转换的精度,通常在坐标转换中采用相似变换(Hermert)的方法,在平面坐标转换过程中一般采用4参数模型。然而当系统误差不可忽略时,该模型处理得到的结果并不理想。本文将半参数模型应用到平面坐标转换中,分别采用4参数模型和半参数模型两种方法对实验数据进行了处理,并进行了对比与分析。实验结果表明：在处理带有系统误差的平面坐标数据时,半参数模型比传统的参数模型更加精确。

关键词：半参数模型;补偿最小二乘;正则矩阵R;平滑因子α;平面坐标转换

doi:10.13442/j.gnss.1008-9268.2015.03.011

中图分类号：P228.4

文献标志码：码： A

文章编号：号： 1008-9268(2015)03-0046-05

收稿日期：2015-01-06

作者简介

Abstract:Coordinate transformation has been playing an essential role in surveying and mapping field,and the selection of model restrict the precision of the transformation directly,generally what we use in the coordinate transformation is similarity transformation (Hermert transformation) method, among them the four parameters model is commonly used in the plane coordinate transformation. when the system error cannot be ignored, however,the result the model get is not ideal.This paper applys a new model, namely the semiparametric model to the plane coordinate transformation, both the parameter model and semiparametric model were used in experimental data processing, as well as comparison and analysis. Experiment result show that Semiparametric model is more accurate and effective than traditional parameter model in dealing with data that cntains system error in plain coordinate transformation.

0引言

半参数模型是上世纪八十年代起发展起来的一种重要的统计模型,它既含有参数分量(描述了观测量中函数关系己知的成分),又含有非参数分量(描述了函数关系未知的模型偏差),可以概括和描述众多实际问题,因此引起了广泛的重视,取得了大量的研究成果[1]。

半参数模型的应用范围较为广泛,在测绘领域主要应用于测量数据处理中,在高精度坐标变换,GPS水准高程拟合等方面都取得了良好的应用效果[2]。坐标转换在测绘领域发挥着重要的作用,遥感图像处理中的几何校正,GIS中将栅格坐标转换为地理坐标的过程中,也必不可少的需要用到坐标转换。将半参数模型引入到坐标转换中是具有很高的理论价值和实际意义[3]。

本文将半参数模型运用到平面坐标转换中,选取了一组有两套坐标数据的公共点,分别采用参数模型和半参数模型进行建模,求解转换参数并进行了精度评定,利用matlab2010a进行数据处理,最后对结果进行了对比与分析。

1半参数模型

统计学上半参数模型被表达为

Y=f(X)+g(X)+Δ,

(1)

式中: Y为观测值; f(X)为参数部分;即观测值与未知参数的函数关系已知的部分; g(X)为非参数部分,即观测值与未知参数的函数关系未知的部分;Δ表示偶然误差[4]。

半参数模型用测量语言描述为

L=BX+S+Δ，

(2)

式中: L为n维观测向量; B维列满秩矩阵; X为t维参数向量;t为必要观测数; S为描述系统误差的n维向量;Δ为n维观测误差向量。

平差准则采用补偿最小二乘准则为

(3)

式中: S为描述系统误差的n维向量; R为正则矩阵,用来估计参数S的某种函数类型;α为平滑因子,在极小化过程中对V和S起平衡作用[5-6]。

按照求条件极值的拉格朗日乘数法构造函数

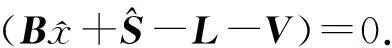
(4)

式中,K为拉格朗日常数。

对方程求偏导数,令

(5)

经过计算,得出如下结果:

非参数估计:

联系人： 赵富燕 E-mail: 946766167@qq.com

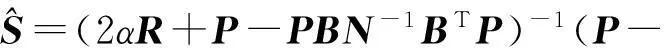
PBN-1BTP-αR)L.

(6)

参数估计:

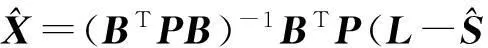
(7)

2平面坐标转换

2.1　平面坐标转换的参数模型

平面坐标转换采用的参数模型为

(8)

式中:θ为坐标系之间的旋转角;λ为尺度因子; (x1,y1)为某点在原坐标系下的坐标; (x2,y2)为经过坐标转换后该点在另一套坐标系下的坐标;Δx, Δy为坐标平移参数;σx,σy分别表示点位坐标X轴,Y轴方向的偶然误差[7-8].

观测方程的线性形式为

vx=1×a+0×b+c×x1-d×y1-x2,

vy=0×a+1×b+c×y1+d×x1-y2,

(9)

式中,

a=Δx,b=Δy,c=λ×cos(θ),

d=λ×sin(θ).

(10)

整理后,平面坐标转换的参数平差模型为

(11)

2.2　平面坐标转换的半参数模型

平面坐标转换的半参数模型为

(12)

式中:Sx,Sy分别表示点位坐标X轴;Y轴方向的系统误差。

观测方程的线性模型为

vx=1×a+0×b+c×x1-d×y1-x2+sx,

vy= 0×a+1×b+c×y1+d×x1-

y2+sy.

(13)

整理后,平面坐标转换的半参数平差模型为

(14)

3算例分析

在x∈(-20,20),y∈(-20,20)的网格点上,实验选取25个均匀分布点,理想认为当前坐标系无误差,为了得到这些点对应的另外一套带有误差的坐标系下的坐标,对它们进行旋转,平移,添加噪声处理。

(15)

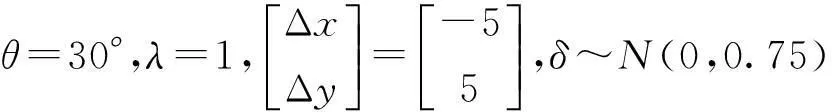
为了尽可能接近实际情况,加入的系统误差中包括线性误差项,指数误差项,还有周期误差项。

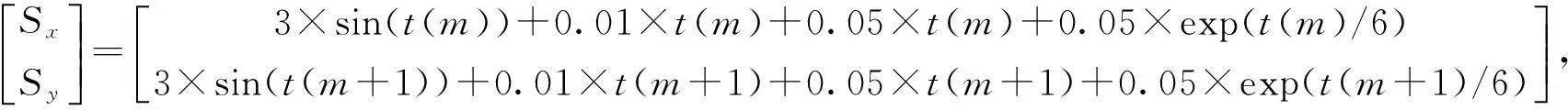
(16)

式中,

t(m)= 2×π×(m-1)/3;

m=1,…,n

(17)

得到的这些点在两套坐标系下的坐标和点位分布图分别如表1和图1所示。

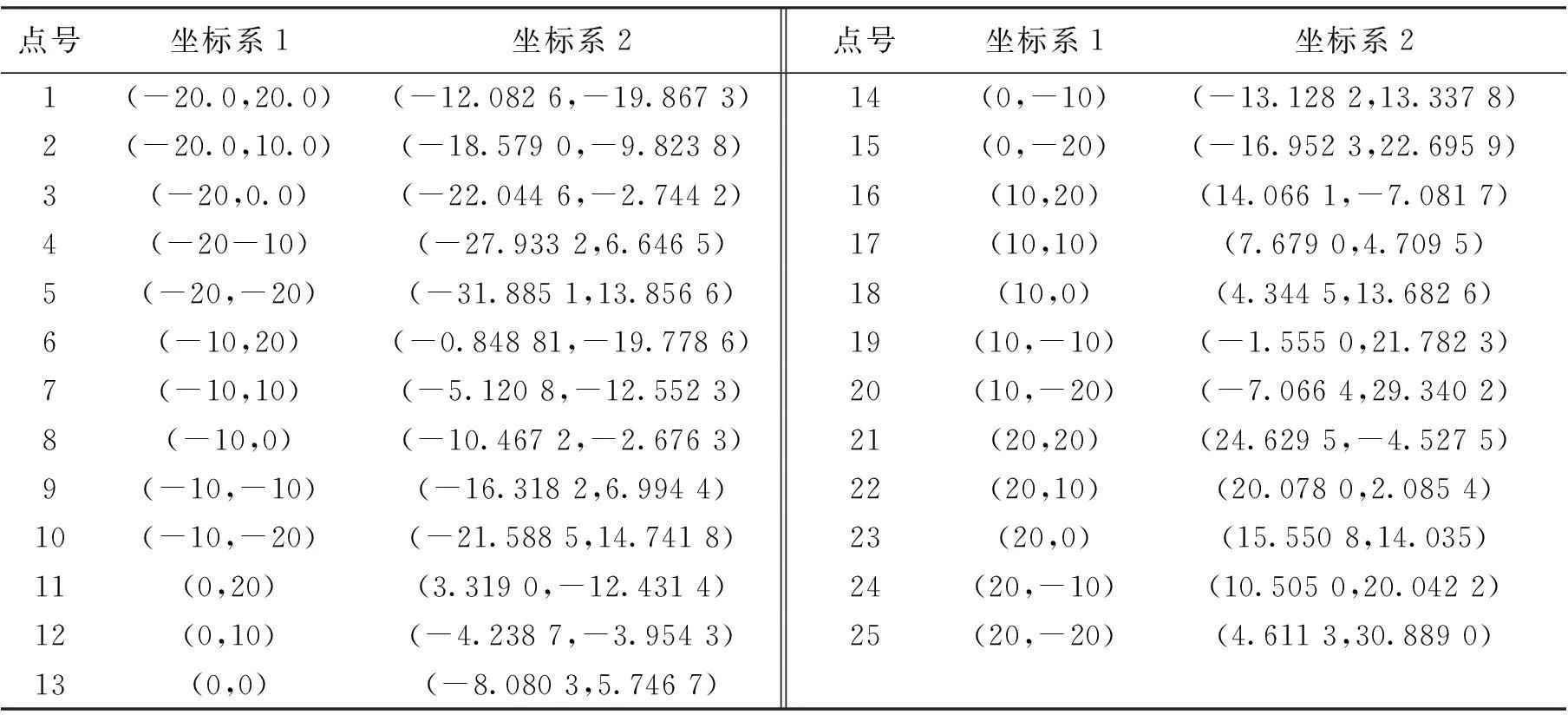
表1　坐标系1和坐标系2下的点位坐标

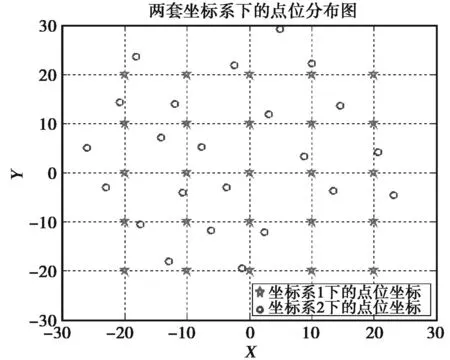
图1　两套坐标系下的点位分布

分别采用参数平差模型和半参数平差模型建模,求解转换参数,并进行精度评定,得到的结果如图2，图3，图4所示。

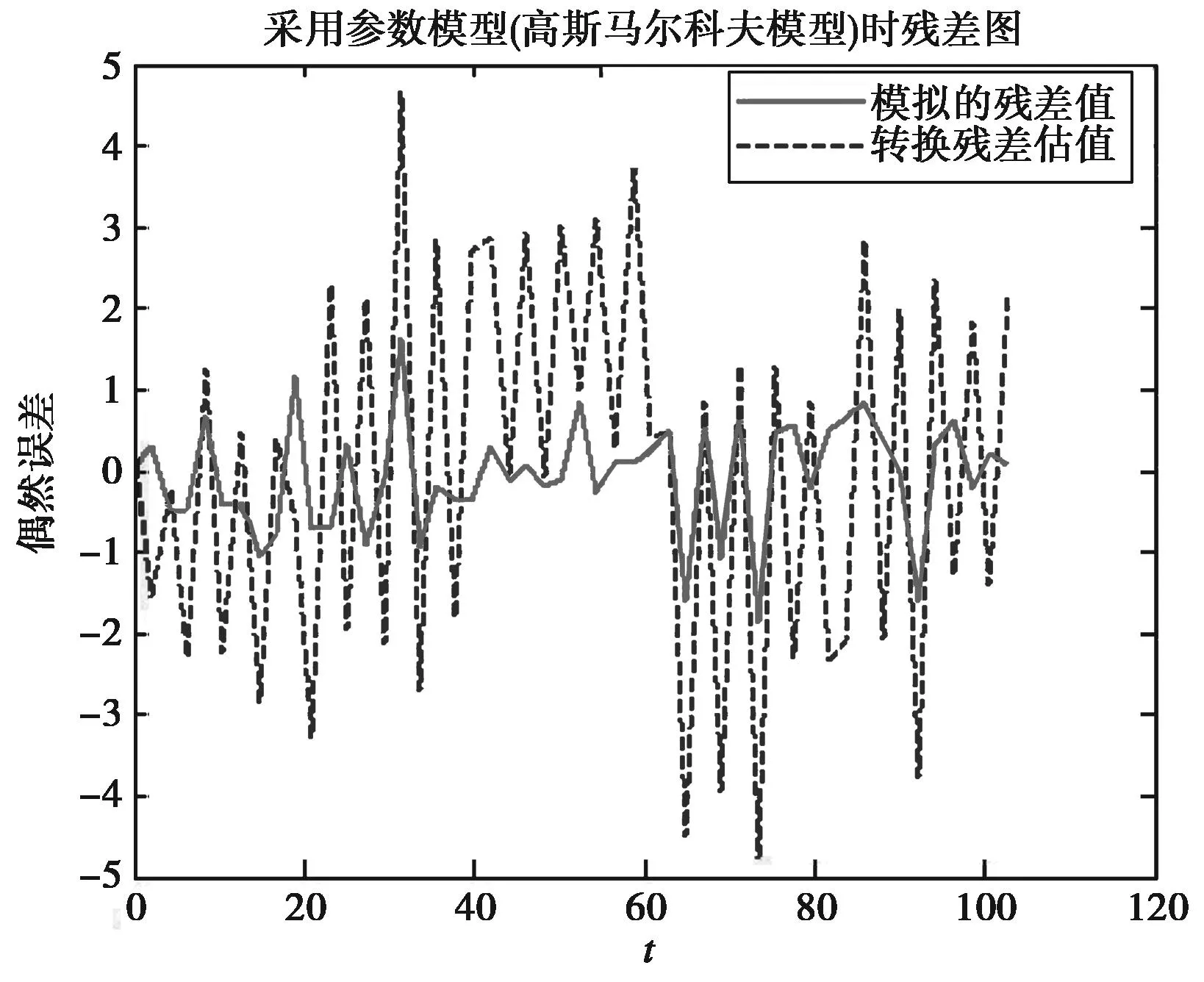
图2　采用参数模型得到的残差

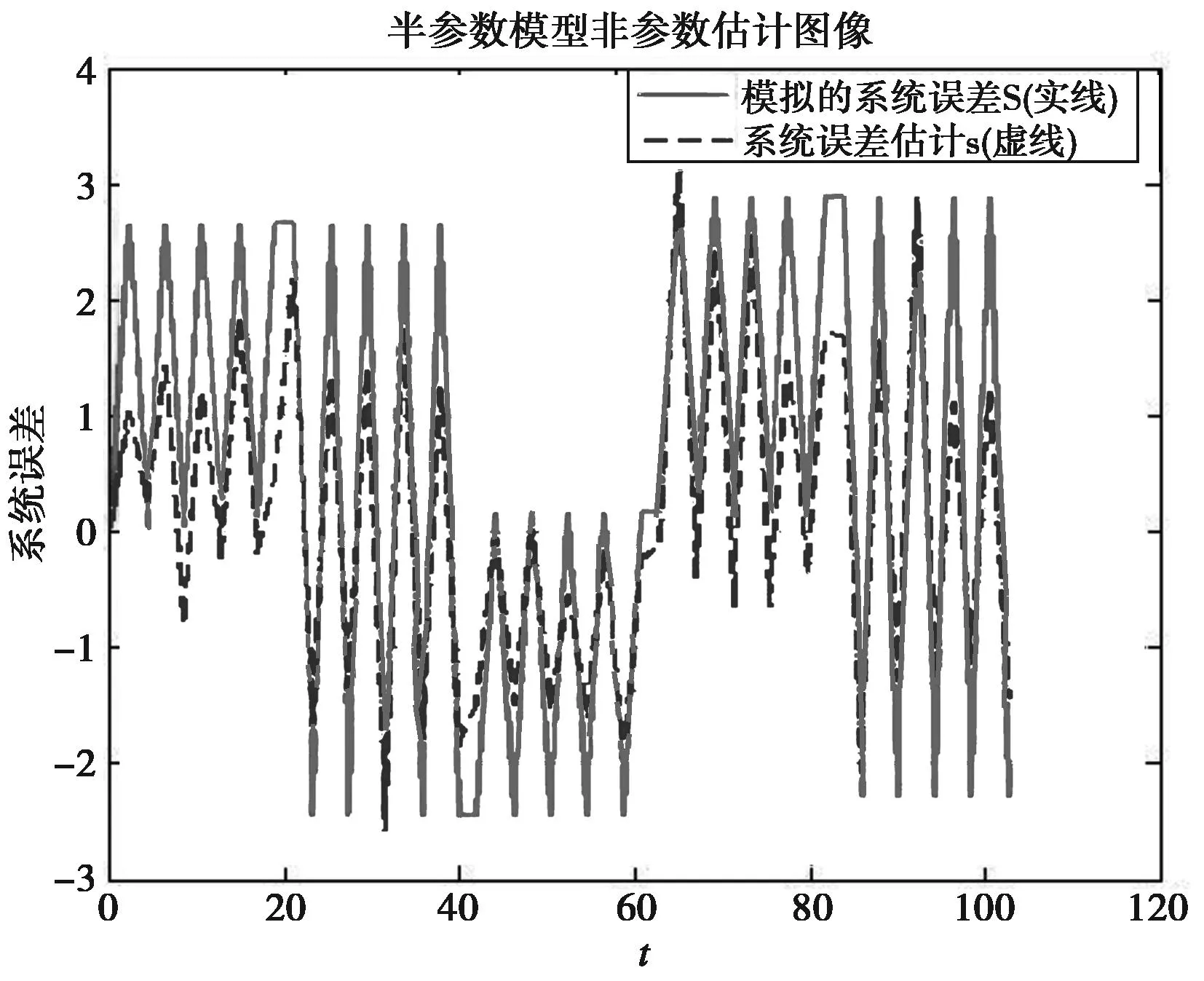
图3　采用半参数模型的系统误差

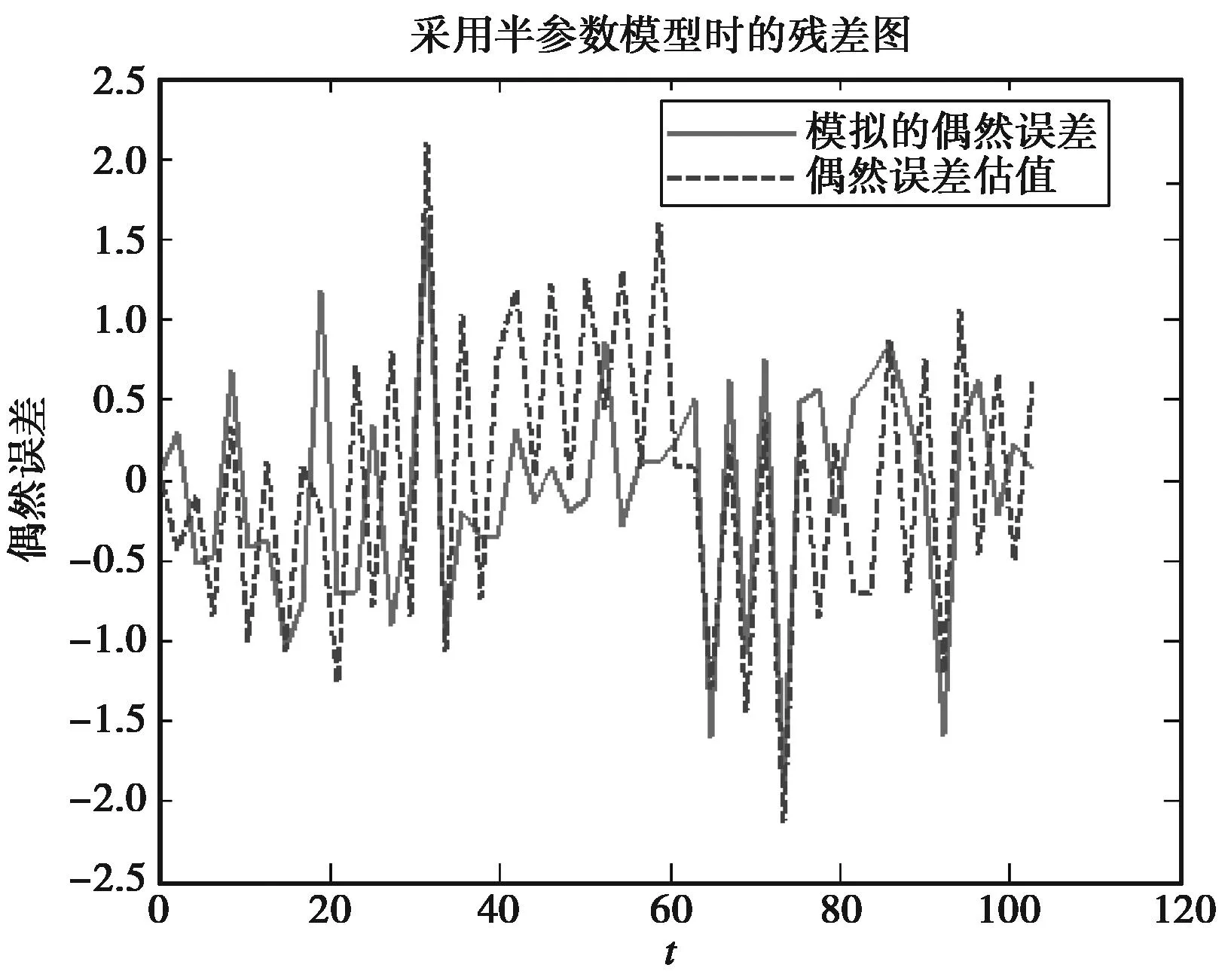
图4　采用半参数模型的残差

从图2中可以看出:采用参数模型处理的残差估值与模拟的残差真值相差较大,利用参数模型求得的残差带有明显的周期性,线性特征。产生这样的结果是因为传统的参数模型将系统误差归入随机误差进行了处理,导致偶然误差带有了这些系统误差的特征。

从图3和图4可以看出:采用半参数平差模型处理得到的系统误差估值和模拟的系统误差之间相差较小,残差估值和模拟的残差在图像中也有较好的符合。

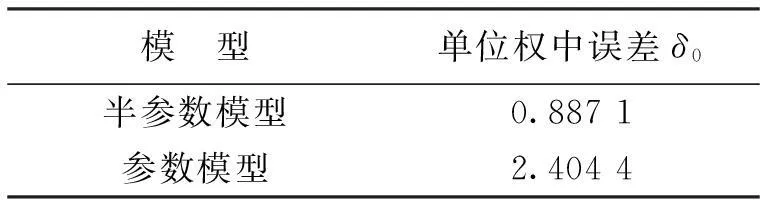
表2　用两种模型处理得到的单位权中误差δ0

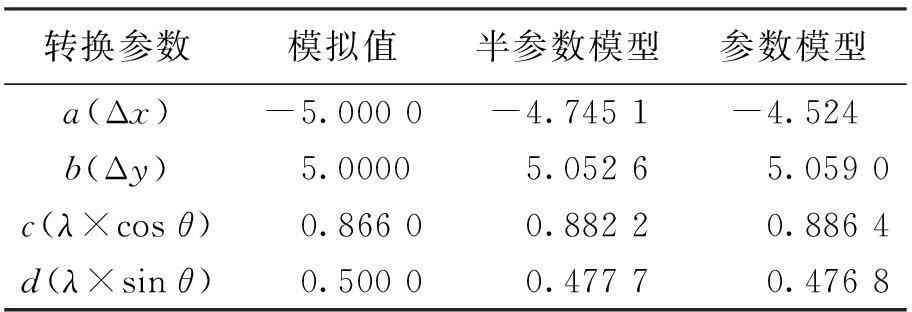
表3　采用两种模型处理得到的转换参数与模拟值比较

从表2中可以看出:采用半参数模型解算出的转换参数的单位权中误差优于采用参数模型解算出的单位权中误差。说明采用半参数模型解算出来的结果精度更高。

从表3中可以看出:采用半参数模型解算出的四个转换参数和采用参数模型解算出的四个转换参数相比更接近于模拟的真值。

4结束语

本文将半参数模型应用到平面坐标转换中,分别采用参数模型和半参数模型两种方法对实验数据进行了处理,并进行了对比与分析。实验结果证明,在平面坐标转换中,当坐标系统存在较大系统误差或者系统误差与偶然误差相比不可忽略时,采用半参数模型比采用参数模型处理得到的结果更优越。同时本实验仍然有一些不足,如果在平面坐标转换中能找到一种普适的R矩阵的构造方法,将使得该模型具有更高的运用价值,取得精度更高的结果,这些都需要在以后的探索,研究中不断地完善。

参考文献

[1] 丁士俊.测量数据的建模与半参数估计[D].武汉:武汉大学,2005.

[2] 杨元喜,张丽萍. 中国大地测量数据处理60年重要进展第二部分:大地测量参数估计理论与方法的主要进展[J]. 地理空间信息, 2010,8(1):1-6.

[3] 孙海燕,吴 云.半参数回归与模型精化[J].武汉大学学报·信息科学版, 2002,27(2):172-174.

[4] 王振杰,欧吉坤,曲国庆,等. 用L曲线法确定半参数模型中的平滑因子[J].武汉大学学报·信息科学版,2004,29(7):651-653.

[5] HANSEN P C. Analysis of discrete ill-posed problems by means of the L-curve [J].SIAM Review,1992,34(4):561-580.

[6] HANSEN P C, O’LEARY D P. The use of the L-curve in the regularization of discrete ill-posed problems[J].SIAM Joumal on Scientific Computing,1993,14(6):1487-1503.

[7] 孔祥元,郭际明,刘宗泉. 大地测量学基础[M].2版.武汉:武汉大学出版社，2005.

[8] 陶本藻,邱卫宁. 误差理论与测量平差[M].武汉:武汉大学出版社,2012.

赵富燕(1990-),女,山东济南人,硕士生,主要从事现代测量数据处理理论及其应用研究。

孙李城(1991-),男,湖北荆州人,硕士生,主要从事测量数据处理,“3S”技术集成与应用研究。

杨兆臣(1988-),男,山东临沂人,硕士生,主要从事GPS,RS,InSAR技术的应用及数据处理研究。

The Application of Semiparametric Model in the

Plane Coordinate Transformation

ZHAO Fuyan,SUN Licheng,YANG Zhaochen

(CollegeofGeomatics,ShandongUniversityofScienceand

Technology,Qingdao266590,China)

Key words: Semiparamertic model; penaliezd least squares; regularization matrix R; the smoothing factor α; plane coordinate transformation