网络RTK网外定位精度分析

2016-01-15吕志伟王兵浩于晓东唐文杰

全球定位系统 2015年3期

关键词：定位精度

石　鑫,吕志伟,王兵浩,于晓东,唐文杰

(信息工程大学导航与空天目标工程学院,河南郑州 450001)

网络RTK网外定位精度分析

石鑫,吕志伟,王兵浩,于晓东,唐文杰

(信息工程大学导航与空天目标工程学院,河南郑州 450001)

摘要：现有网络RTK在网内的定位精度已经得到充分认证,能够达到厘米级,但网外的定位精度缺乏有效验证,对流层、电离层等误差的空间相关性限制了网外定位的作业距离。对网络RTK网外定位精度进行了详细分析,采用线性模型外推空间相关误差,用虚拟参考站技术搭建网络RTK,在网外不同位置检验定位精度。结果表明:定位精度随着用户离基站网距离的增加而降低,在参考站网络模糊度固定的情况下,用户位于网外20 km范围内时,网络RTK基本能提供厘米级的定位精度,超过30 km时,定位精度明显下降,且波动较大。

关键词：网络RTK；虚拟参考站；空间相关误差；线性内插；定位精度

doi:10.13442/j.gnss.1008-9268.2015.03.006

中图分类号：P228.4

文献标志码：码： A

文章编号：号： 1008-9268(2015)03-0025-06

收稿日期：2015-01-19

作者简介

Abstract:It has been certified that network RTK can achieve CM positioning within stations network, but the precision outside of network lack of verification, and the work distance limited by the correlation of errors such as ionosphere and troposphere. The Virtual Reference Station and Linear Interpolation Model were used to build network RTK, tested positioning errors comprehensively on different positions. The result shows that positioning precision decreases along with the increase of the distance between user and stations network. And if the ambiguity of the reference station network has been fixed, the network RTK can provides CM positioning service when users locate within 20 km outside of the network, and the precision decreases and fluctuates obviously while the distance over 30 km.

0引言

网络RTK是近年来出现的新技术,其数据处理的核心包括三个方面:参考站网络模糊度解算技术、距离相关误差建模、改正数发布。常规RTK能够实现高精度定位,由一台基站和若干台流动站组成,通过流动站和基站之间的差分即可获得厘米级的定位精度,但其作业距离短,限定其作业范围的主要因素是基站和流动站误差的空间相关性,随着流动站与基站之间距离的增加,各种误差的空间相关性迅速下降,导致观测时间增加,甚至无法固定整周模糊度而只能获得浮点解。网络RTK很好的解决了这个问题,进行定位服务时,首先利用流动站周围的几个基站的观测值以及已知坐标解出基站之间的残余电离层延迟、残余对流层延迟等,这些残差可统称为综合误差,然后根据用户的概略位置估计出用户与基站之间的综合误差,当基站间的距离达到50 km至100 km时,用户仍能获得厘米级的定位精度[1]。作为空间数据基础设施,CORS系统的建设逐渐成为数字城市和信息化建设的重要内容,许多城市已将CORS的建设列入政府基础设施计划[2],深圳、上海、广州、昆明等城市已分别建立了城市CORS系统,系统的精度也得到了相应评定,但大部分都是针对网内的情况,网外的精度评定相对较少。本文采用目前最为成熟的虚拟参考站技术(VRS)搭建网络RTK,用线性内插法(LIM)构建空间相关误差数学模型,对网外的定位精度进行了详细分析。VRS和线性内插法是现阶段建设网络RTK最为常用、成熟的技术,因此,本文的精度分析结果具有一定参考价值。

1LIM模型的构建

随着高精度应用领域对精度的要求不断提高,对流层、电离层延迟等成为了定位精度进一步提高的主要因素[3]。LIM模型是通过平面位置反映空间相关性的,是一个二维模型,基站网中各基线的整周模糊度固定后,即可求得各基线的空间相关误差,根据基站之间相对位置关系以及基线的空间相关误差确定外推系数,经验证,LIM模型在网内对电离层和对流层的改正精度都达到厘米级[4],其模型的数学过程为

(1)

式中：ΔVi,n为外推时用到的相关基线的误差项；[ΔXi,nΔYi,n]为相关基线二维坐标向量； a和b为外推系数,当参考站数量超过3个时,a和b可由下

--------------------

联系人：石鑫E-mail:shixinkd@163.com

式求出:

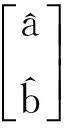
(2)

P为各基线上空间相关误差的权阵,外推系数求出之后,即可求得虚拟参考站与主参考之间的空间相关误差:

(3)

式中，ΔXvrs,n和ΔYvrs,n为VRS与主参考站的坐标差。

LIM模型最初是为修正电离层延迟而提出的,可以修正区域相关的电离层延迟,同时,LIM也是较优的对流层延迟误差改正模型[5],经验证,LIM的平面改正精度是现有内插模型中最高的[6],所以,采用LIM模型外推空间相关误差是完全可行、可靠的。只有准确的求得用户与主参考站之间的误差项后,才能快速的解算出用户与VRS间的整周模糊度,从而减少用户的初始化时间[7]。数据处理中心根据用户的位置选定改正区域,用改正区域中的基线建立LIM改正模型。改正区域的构建有全网改正、三角形改正、子网改正三种方法,综合考虑各种因素,三角形改正是目前最实用、最可靠的改正方法[8]。当用户位于某个三角形内时,即是网内定位,当用户不处于基站网中的任一三角形中时,即是网外定位,需要选用一个外推三角形来构建LIM模型。

如图1所示,用户在网外有定位请求时,数据处理中心根据用户的概略坐标选择重心离用户最近的那个三角形作为外推三角形,再选择此三角形中离用户最近的那个站作为主参考站,三角形中以此主参考站为端点的两条基线为外推基线(图中浅色基线),这样就能确保误差有一定的空间相关性,LIM模型就能有效改正流动站与主参考站间的相关误差。随着用户离基站网距离的增加,误差的空间相关性下降,模型的改正精度就会降低,从而导致定位精度下降。图2是天津CORS网的部分基站分布图,为探讨外推精度与距离的关系,选取DZ02、TJA2、KC03、YC01、KC02五个点组成一个子网,CH01、DZ01作为子网的网外点,其中CH01距子网5.7km,DZ01距子网31.2km,选取YC01为主参考站,通过基线解算可以得到各基线综合误差,同时得到CH01、DZ01两个网外点与主参考站间的综合误差,用子网基线的综合误差外推CH01、DZ01与主参考站间的综合误差,将外推结果与解算结果进行对比,以反映外推精度的高低。图3示出了CH01、DZ01处PRN23卫星的1h综合误差(采样间隔1s)外推精度统计情况。

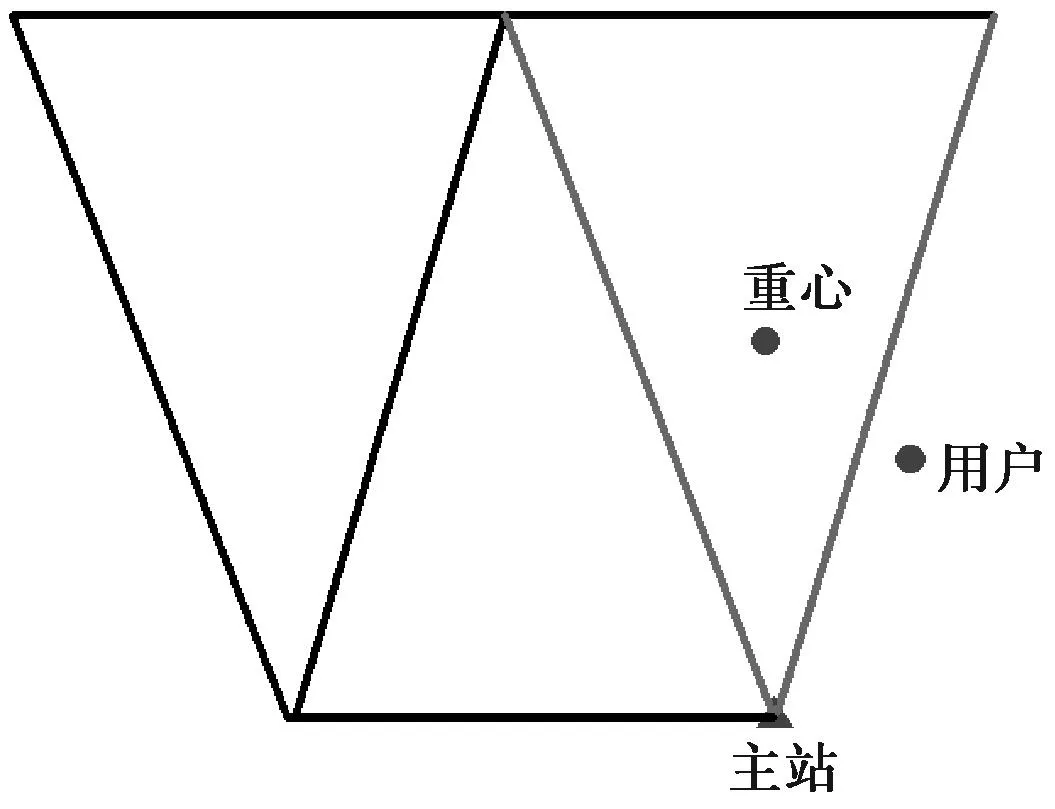
图1　外推三角形

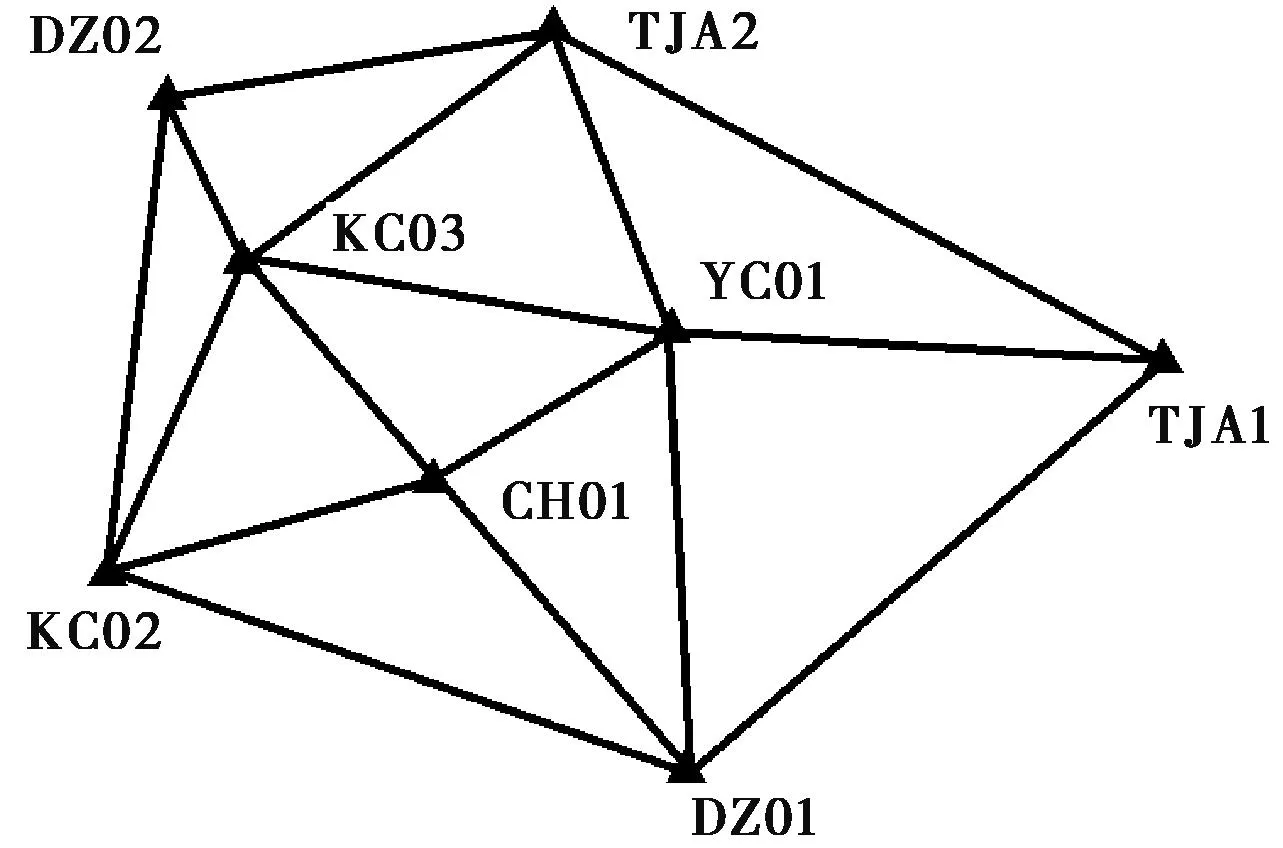
图2　基站网

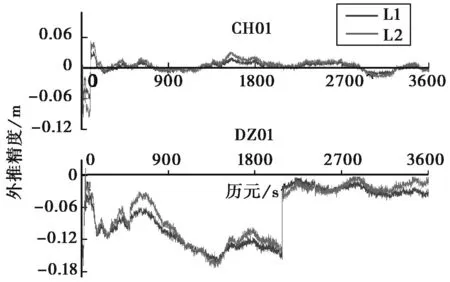
图3　外推精度对比

从图3可以看出,CH01处的外推精度较高且稳定,DZ01处的外推精度较低。图3表明,空间相关误差的外推精度和用户离基站网的距离是相关的,通常是距离越近,外推精度越高,随着距离的增加,外推精度也随之下降。当用户和基站网的距离过大时,LIM模型很难反映误差的空间相关性,最终导致用户无法获得固定解。

2VRS技术实现

VRS的基本原理是在用户位置附近虚拟出一个参考站VRS,通过相应数学模型构建出VRS的观测值,用户利用VRS观测值进行常规RTK定位。网络RTK通常由基准站网、数据处理及播发中心、数据通信链路等部分组成,数据处理中心实时解算基准站网基线,估计各基线的综合误差。为了保证一定的定位精度,必须通过模型对空间相关误差予以消除[9]。当用户有定位请求时,首先通过单点定位获取自己的概略坐标,并将此坐标发送给数据处理中心,数据处理中心收到用户概略坐标后,将此位置设为VRS,并根据用户的位置在基站网中选出一个主参考站以及若干副参考站,由这些参考站构成相关基线,对相关基线的综合误差进行误差建模,内插出VRS与主参考站之间的空间相关误差,最后构建出VRS的观测值并发送给用户,具体步骤如下[10]:

1) 基站网络中的所有参考站将观测得到的原始数据实时传送给数据处理中心。

2) 用户以NEMAGGA的形式将概略坐标发送给数据处理中心,数据处理中心据此产生虚拟参考站。

3) 数据处理中心根据用户位置选取一组参考站。

4) 依据选取参考站基线结算结果,数据处理中心对误差源进行建模计算,得到VRS处误差改正数。

5) 结合参考站观测值和VRS误差改正数构建出VRS处的虚拟观测值,并以标准RTCM协议发送给用户,用户接收到虚拟观测值完成差分定位。

虚拟参考站位置一般通过流动站用户接收机的单点定位解确定,故VRS与流动站间距离通常只有十几米,只要能够生成VRS的观测值或RTCM差分改正数,就可以在VRS和用户站间实现短距离常规差分解算[11]。VRS相位、伪距观测值的构建模型为[12]

(4)

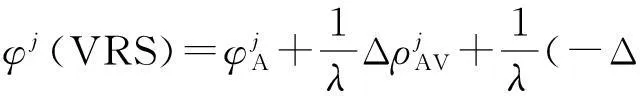
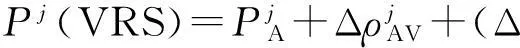
Δ).

(5)

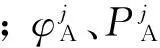
(6)

(7)

目前,大多数网络RTK系统都采用LIM模型和VRS技术来搭建,经验证,当用户在网内时,能够实现厘米级定位精度。在图2中,选取KC03、YC01、CH01三个点作为用户位置,在三个站上进行数据观测,时长为1h,采样间隔1s,利用网络RTK实时解算用户坐标。其中KC03、YC01、CH01的内插三角形分别为DZ02-TJA2-KC02,CH01-TJA2-TJA1,DZ01-YC01-KC02,将解算结果与精确坐标进行对比,置信区间取95%,统计结果如表1所示。

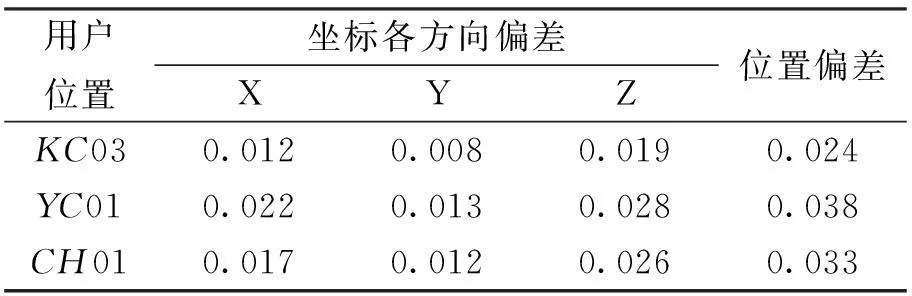
表1　网内定位精度统计

从表中可以看出,在置信区间为95%的情况下,网络RTK在网内的定位精度达到厘米级,定位精度较高。网外定位相对于网内有着先天的不足,因为当用户处在网外时,基准站只分布在用户的某一侧,而不是像网内那样周围都分布有基站,这样在用外推模型求用户位置处空间相关误差时,外推精度受距离的影响较大。

3网外定位精度分析

网络RTK提供网外定位服务时,实际上只用到了外推三角形的三个基站,所以在实验时,用户位置确定后,在基站网中根据相关规则选择一个不包含用户的三角形作为外推三角形,用此三角形三个基站的观测数据构建VRS虚拟观测值,这样就能搭建网外定位的环境。为了便于检验定位精度,将用户的位置设在已知基站上,以基站的精确坐标检验定位结果的精度。根据图2的网形,设计了6种组合进行实验分析，如表2所示。同样,对用户进行连续的1h实时定位,采样间隔为1s.

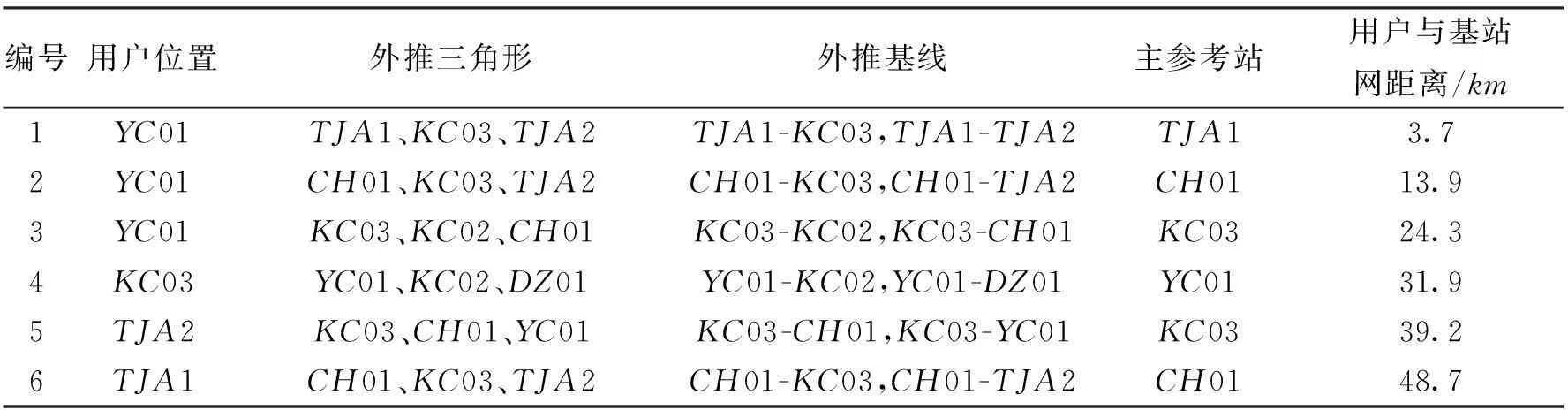
表2　实验设计

上述6种组合的主要变量为用户至基线的距离,其范围从几公里至几十公里不等,最近离基站网3.7km,最远48.7km,随着距离的增加,空间相关性必然下降,从而导致最终的定位精度降低。结果表明,用户离基站网越近,定位精度越高。各实验定位结果精度(与精确坐标相比)如图4所示。

图4中,前三个实验的结果较好,X、Y、Z三个方向绝对偏差均在厘米级,后三个实验的结果较差,其中,实验5、实验6中,由于用户离基线网太远,外推模型无法正确反映空间相关性,构建出的虚拟观测值就会出现较大偏差,所以最后的结果较差。将每个历元的定位结果与精确坐标进行对比,求出位置偏差,各实验的精度统计如图5所示。

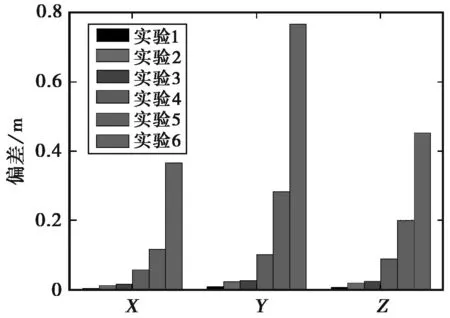
图4　坐标各方向偏差

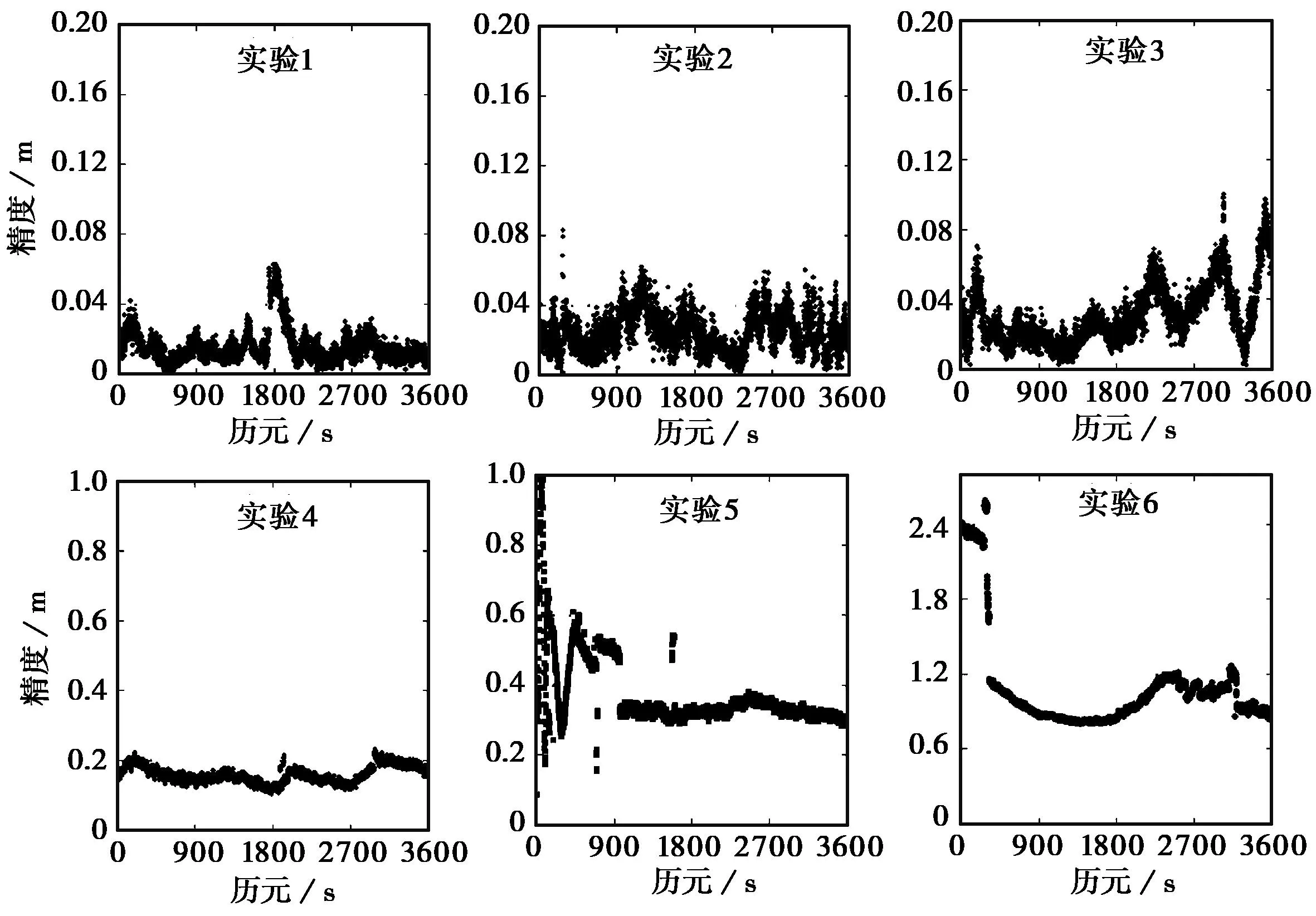
图5位置精度

从图5可以看出,实验1每个历元的定位精度维持在6cm内,实验2除了个别历元偏差较大外,其他历元基本都维持在6cm内,实验3保持在10cm内,实验4、实验5的定位结果维持在分米级,实验6属于米级,其中实验5和实验6不仅定位精度差,而且波动较大,精度无法稳定在某一个量级。根据图5的精度对比情况可以得知,随着用户与基站网距离的增大,定位精度逐渐下降。表3示出了E、N、U方向的精度统计(置信区间95%),其表现出了与位置精度一致的变化趋势:

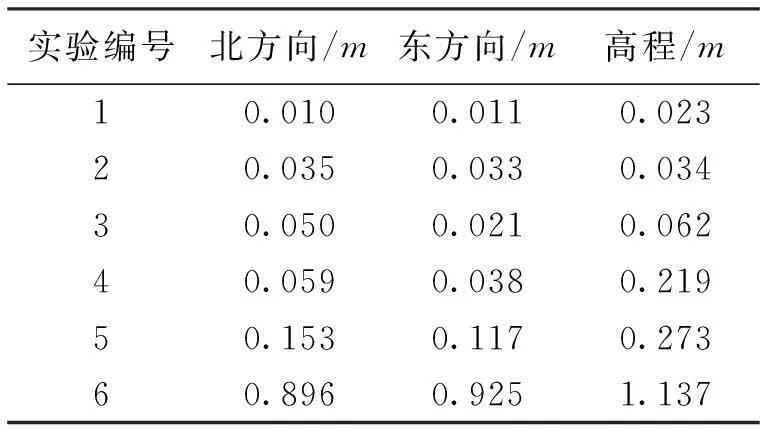
表3　三维精度

需要指出的是,实验4、实验5和实验6中,由于离基站网较远,导致空间相关误差外推精度不高,从而难以获得固定解,实验4中绝大多数结果都是浮点解,而实验5、实验6则全是浮点解。所以,空间误差的外推精度对网外定位非常重要,直接影响整周模糊度的固定情况。经进一步实验,得到了定位精度与用户离基站网距离的大致关系图(正常大气状态),如图6所示。

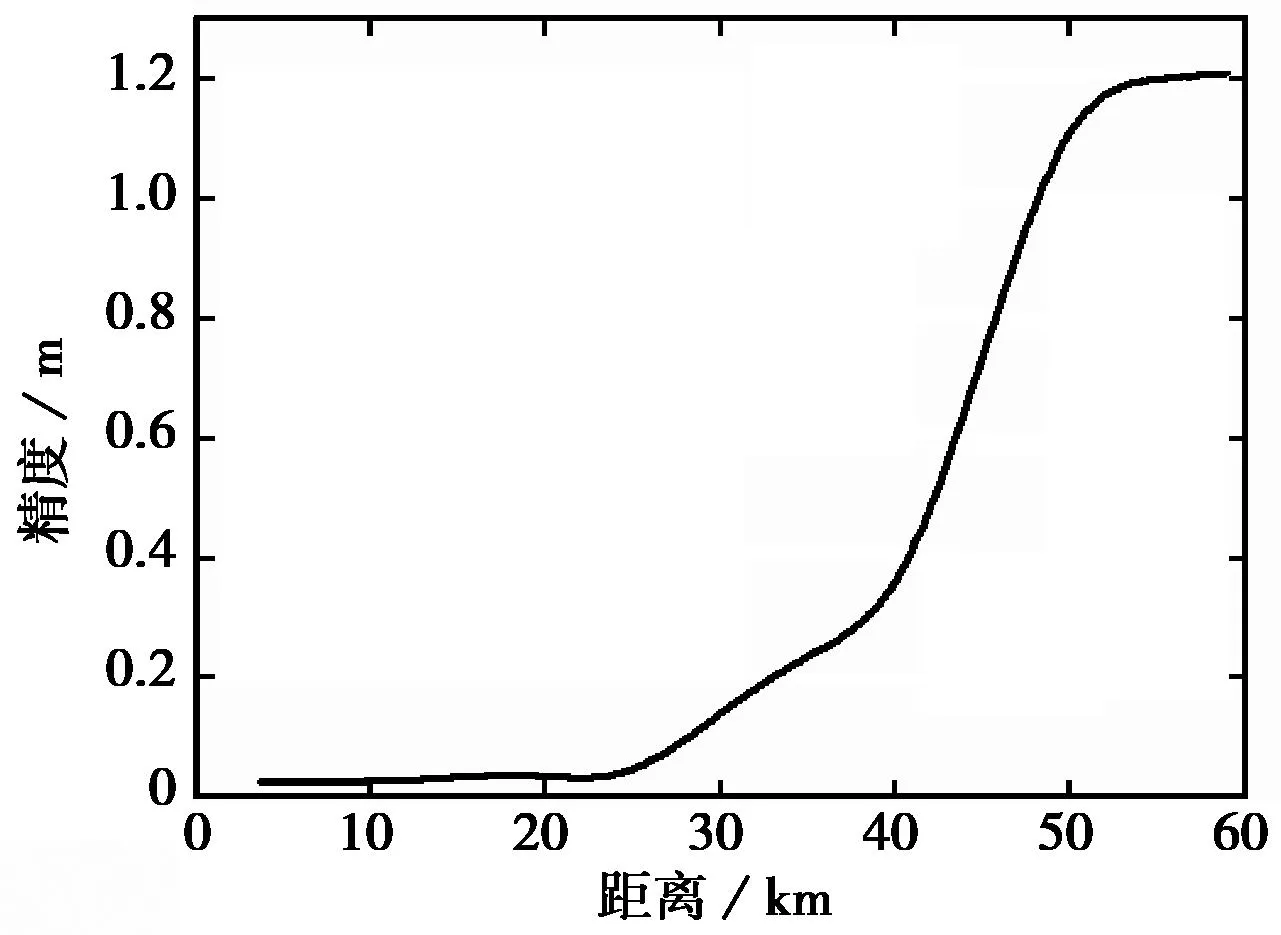
图6　定位精度随距离变化图

从图6可以看出,当用户与基站网的距离在20km内时,定位精度达到厘米级,超过20km后随着距离的增加精度逐渐下降,当距离接近23km后,精度迅速降低。这说明在正常大气状态下,综合误差空间相关性的有效距离不超过30km.

4结束语

由于误差的空间相关性,外推精度和用户离基站网的距离是相关的,用户离基站网越近,外推精度越高,定位精度较好,随着用户与基站网距离的增加,各种误差的空间相关性减弱,外推模型不能正确反映真实误差之间的空间相关性,从而导致最终定位精度变差。实验结果表明,当用户位于网外20km范围内时,基于LIM的网络RTK基本能提供厘米级的定位精度,超过30km时,定位精度就很难得到有效保障。

参考文献

[1]李征航,黄劲松.GPS测量与数据处理[M].武汉:武汉大学出版社,2010:168-169.

[2]刘经南,刘晖.连续运行卫星定位服务系统——城市空间数据的基础设施[J].武汉大学学报,2003,28(3):259-264.

[3]李施佳, 蔡昌盛, 李佳霖, 等. 对流层投影函数对精密单点定位精度的影响分析[J].全球定位系统,2013,38(5):22-26.

[4]吕志伟.基于连续运行基准站的动态定位理论与方法研究[D].郑州:信息工程大学,2010:110-118.

[5]谢建涛.VRS改正数算法研究及精度分析[D].郑州:信息工程大学,2013:50-54.

[6]Al-SHAERYA,LIMS,RIZOSC.Investigationofdifferentinterpolationmodelsusedinnetwork-rTKforthevirtualreferencestationtechnique[J].JournalofGlobalPositioningSystems,2011,10(2):136-148.

[7]邱蕾,陈远鸿,段艳霞.GPS网络RTK流动站的电离层误差改正分析[J].大地测量与地球动力学,2010,30(1):56-60.

[8]黄丁发,周乐韬,李成钢,等.GPS增强参考站网络理论[M].北京:科学出版社,2011:75-77.

[9]张成军.虚拟参考站误差分析与算法研究[D].郑州:信息工程大学,2005:47-56.

[10]吴俐民,定仁军,李凤霞.GPS参考站系统原理与应用[M].成都:西南交通大学出版社,2008.

[11]黄丁发,李成钢,刘经南，等.GPS/VRS实时网络改正数生成算法研究[J].测绘学报,2007,36(3):256-261.

[12]李成钢.网络GPS/VRS系统高精度差分改正信息生成与发布研究[D].成都:西南交通大学,2007:34-37.

石鑫(1990-),男,四川成都人,硕士生,研究方向为网络RTK相关算法研究.

吕志伟(1974-),男,江西赣州人,副教授,主要从事卫星精密定位方向的研究。

王兵浩(1989-),男,河北衡水人,硕士生,主要从事网络RTK、GNSS融合相对定位相关方面研究。

于晓东(1990-),男,河北邯郸人,硕士生,主要从事网络RTK相关算法的研究。

唐文杰(1991-),男,安徽宣城人,硕士生,主要从事网络RTK及行人导航方面研究。

Analysis of Net Work RTK Positioning Precision Out of Network