三个课例看计数器对核心概念建构的价值
2016-01-14陈曦

摘要:计数器在小学数学课堂上必备的教学工具之一,常常用于数的认识、数的运算等课的教学中,其在帮助学生建构十进制、位值制概念及相同计数单位数直接加减等核心概念的学习中有着独特的文化含义和价值。
关键词:计数器 核心概念 建构 价值
DOI:
10.16657/j.cnki.issn1673-9132.2016.01.151
计数器在小学数学课堂上必备的教学工具之一,常常用于数的认识、数的运算等课的教学中,其在帮助学生建构十进制、位值制概念及相同计数单位数直接加减等核心概念的学习中有着独特的文化含义和价值。笔者通过最近听过的三个课例谈谈计数器对以上核心概念建构的价值。
课例一:11-20各数的认识(青岛版课程标准实验教科书小学数学一年级上册第五单元)
11-20各数的认识是10以内数的认识的延续,也是认识更大自然数的基础,是学生建立数位概念的重要节点。一年级学生大多数能按顺序从1数到20,甚至更多,但学生对于计数单位“十”“满十进一”、位值等概念还很模糊,大多数学生不理解“位值原理”。因此,这节课让学生体会体验计数单位“十”产生的必要性是一个核心点。
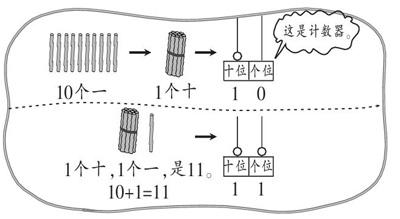
<F:\冯旻\学周刊\2016年\1期\1 4-125\陈曦-3.tif><F:\冯旻\学周刊\2016年\1期\1 4-125\陈曦-3.tif><F:\冯旻\学周刊\2016年\1期\1 4-125\陈曦-3.tif><F:\冯旻\学周刊\2016年\1期\1 4-125\陈曦-3.tif><F:\冯旻\学周刊\2016年\1期\1 4-125\陈曦-3.tif><F:\冯旻\学周刊\2016年\1期\1 4-125\陈曦-3.tif><F:\冯旻\学周刊\2016年\1期\1 4-125\陈曦-3.tif><F:\冯旻\学周刊\2016年\1期\1 4-125\陈曦-3.tif><F:\冯旻\学周刊\2016年\1期\1 4-125\陈曦-3.tif><F:\冯旻\学周刊\2016年\1期\1 4-125\陈曦-3.tif><F:\冯旻\学周刊\2016年\1期\1 4-125\陈曦-3.tif> [10个一][1个十][1 0][这是计数器。] [十位 个位][1 1][十位 个位]<F:\冯旻\学周刊\2016年\1期\1 4-125\陈曦-3.tif><F:\冯旻\学周刊\2016年\1期\1 4-125\陈曦-3.tif>[1个十,1个一,是11。
10+1=11]
教学片断:解决“沙滩上有多少只海鸥”—— 认识数“11”
1.数海鸥:先估计再数数——突出数法指导,渗透数数策略。
2.摆小棒表示数——体验计数单位“十”产生的必要性。
3.用计数器表示数。——建立1个“十”和10个“一”的不同表象。
(1)计数器上拨出11。
(2)增加数位,对比小棒法认识计数器上的个位和十位。
教师:计数器上还有很多的珠子,它们坐的位置不一样,表示的意义就不一样。十位上的珠子是专门用来表示几个十的,十位上坐上 1 颗珠子,它就表示 1 个十,就是刚才我们捆起来的一捆小棒;个位上的这些珠子是专门用来表示几个一的,个位上坐上 1 颗珠子,它就表示 1个一。
4.用符号表示数——把计数器上表示的数抽象化,就是数的书写形式。
价值分析:这里计数器的使用是必需的,数学思维一般通过数学活动要揭示(发现、掌握)的新的、未知的东西是什么。有些新的、未知的东西,学生自己能够发现,比如海鸥有11只,可以通过数知道。但学生不可能发现新的计数单位 “十”。因此,计数器从一个数位扩展到两个数位,并通过比较小棒摆11和计数器拨11的两个活动,让学生体会其相同点和不同点。因为同一个数字符号在不同的数位上表示不同的数值,所以,用较少的数字符号可以表示很多数,古人用位值制就将数学的简洁、智慧与优越彰显无遗。
课例二:9加几(青岛版课程标准实验教科书小学数学一年级上册第七单元)
“9加几”作为20以内进位加法的第一课时,是一节种子课。这样一节种子课的教学价值不言而喻。因此教师不仅要熟悉教材中的每个知识点、清楚知识链接的逻辑体系,也要厘清9加几的算理、算法分别是什么、知识生长点在哪里,才能更好地引导学生学可以生长的数学。为此,我翻阅了相关资料,对“9加几”中涉及算理、算法、十进制等文化。
教学片断:探究9+6=
方法一:接着数
生1:1,2,3……15。
生2:10,11,12,13,14,15。
方法二:凑整
生1:老师我是这样做的。我先算的10+6=16,9+6=15。(板书)
方法三:凑十
1.摆小棒“凑十”
生1:我从6拿出1个一,给9,9变成10,10再加上剩下的5就合成了15。
生2:我把这个1和9合成了10,10再加上剩下的5,就是15。
师:(课件动画)我们一起来看看他是怎么做的。9+6,我们先从6里面拿出1个一,给9,9凑成1个十,再和原来的5个一合成15。
师:既然是把9凑成10,我们就叫它凑十法吧。
2.计数器感知的必要性。
师:你能在计数器上拨出9+6吗?
先拨9,再拨6——十位上拨出6个十(不行)——不会拨,因为个位只剩1个。由此得出这个6必须拨在个位上,可是个位上只剩下1个了。那怎么拨6,想办法。
先拨一个,用十位上的1个代替个位上的10个。(学生交流:为什么?十位上因为10个一,就是1个十。)
再在个位上拨剩下的5个了。(学生交流:为什么+6,却拨5个)
师:9+6。先拨9,9+6再先拨其中的1,这样就10个一了,用.十位上的一个代替个位上的10个,再在个位上拨剩下的5个,听明白了吗?
3.抽象算法。
……
价值分析:该课例在处理9+6=?这一个核心知识点的建构时通过摆小棒、圈图、用计数器等方法,利用数的组成、十进制计数策略等不仅注重了凑十的形象思维,还突出满十进一的十进制计数法,诠释了“凑十法”与十进制计数法之间的联系,把表象转化成学生头脑中的思维程序,使学生不仅知其然, 还要知其所以然, 从而保证了在进位加法中的有效迁移,实现了核心知识以生长的姿态的主动建构。
课例三:两位数加两位数(不进位)(五年制青岛版小学数学教科书一年级下册第六单元)
分析两位数加两位数(不进位)的教材,不难发现算法可多样,重点介绍笔算。通过对学生的了解分析,我着重关注了两点:一是如何将学生更习惯的口算的方法与笔算对接;二是如何将算理直观,算法抽象;三是课本中的“在竖式计算时,相同数位要对齐。”如何帮助学生理解建构?我在对上述问题深度思考的过程中,觉得计数器更加接近笔算的样子,那么借助计数器帮助学生直观算理,算法抽象应该效果会好。
<F:\冯旻\学周刊\2016年\1期\1 4-125\陈曦-3.tif><F:\冯旻\学周刊\2016年\1期\1 4-125\陈曦-3.tif><F:\冯旻\学周刊\2016年\1期\1 4-125\陈曦-3.tif><F:\冯旻\学周刊\2016年\1期\1 4-125\陈曦-3.tif><F:\冯旻\学周刊\2016年\1期\1 4-125\陈曦-3.tif><F:\冯旻\学周刊\2016年\1期\1 4-125\陈曦-3.tif><F:\冯旻\学周刊\2016年\1期\1 4-125\陈曦-3.tif><F:\冯旻\学周刊\2016年\1期\1 4-125\陈曦-3.tif><F:\冯旻\学周刊\2016年\1期\1 4-125\陈曦-3.tif><F:\冯旻\学周刊\2016年\1期\1 4-125\陈曦-3.tif><F:\冯旻\学周刊\2016年\1期\1 4-125\陈曦-3.tif> [26
12][+][38][十位][十位]
[竖式计算也叫笔算,也就是把
口算的过程用笔写出来。
例如:26+12][6+2=8
20+10=30
30+8=38] [26
12
8
30
38][+][26
12
38][+]
价值分析:此课例中,计数器实际就是一个半抽象的竖式原型,因此计数器在直观算理,算法抽象中起到了极其重要的作用。本课有序的呈现了估算、口算、笔算的三算过程,以“口算——在新知生长点处形成横式算理、摆小棒——形成竖式算理原型、计数器——构建竖式算理模型、笔算——实现算理与算法的融合“四个活动为主线,通过三算四活动让学生实现算理和算法的完美对接,多表征沟通,数形结合直观,多途径促进学生的形象思维向抽象思维过渡,有效的建构了”相同计数单位的数直接相加“的核心概念,积累了数学活动经验。
(责编 赵建荣)
