加强思维训练 提高数学素质
2016-01-14林阳清
林阳清
摘要:小学数学教学不仅要让学生获得相应的学习知识,还需要养成学生的学习习惯,培养其自主学习的能力,形成良好的思维品质,让学生能够运用所学知识,解决生活中的数学问题。因此,在平时教学中,教师要格外注意学生思维能力的培养。数学思维具有很多特点,比如灵活性,直觉性,发散性等,所以,在数学教学中,重视培养学生的思能力,是提高学生数学素质的重要方向,结合本人教学经验,谈一些体会。
关键词:小学数学 教学任务 思维训练 数学素质
DOI:
10.16657/j.cnki.issn1673-9132.2016.01.130
一、培养思维的独立性,提高学生自主探索的能力
创新是数学思维的主要特点,但却需要学生具有较强的独立思维能力。而学生的这种独立性如何培养?我通过在日常教学中的经验总结出,教师应为学生选择一些具有较强探索性的数学重点或问题,鼓励和激励所有学生积极参与,让他们感受获取知识的过程,这样既激发了学生学习的积极性,又充分发挥了学生的主体作用。
例如,在进行“三角形面积”教学过程中,课前我先让每个学生自己准备完全一样钝角三角形、直角三角形、锐角三角形各一对,上课时学生每4人一组,让学生先用多对三角形来摆一摆,拼一拼,看看能不能摆出以前学过的图形。通过分组讨论,同学们分别拼出长方形、正方形、平行四边形,然后问一问学生们这三种图形有什么关系呢?得到学生的回答:长方形、正方形是特殊的平行四边形后再放手让学生讨论并思考:拼成的平行四边形的底和高与三角形的底和高有什么关系?通过学生自己认真观察,学生会发现平行四边形的底相当于三角形的底,平行四边形的高相当于三角形的高。最后通过平行四边形的面积和三角形的面积的关系,学生自然而然就推导出三角形的面积公式。这样的安排,使学生真正经历了知识的发生与形成的过程,让每个学都能够积极参与教学过程从而激发了学生学习的积极性和主动性。
二、训练思维的广阔性,提高学生解决问题的应变力
数学思维的广阔性是指思维活动作用范围的广泛和全面的程度。它表现为思路开阔,能全面的分析问题、多方向、多层次的思考问题多角度的研究问题。在解题时,将问题逐步引申,是解题思路顺利迁移,不仅能巩固所学的数学知识,而且能较好的培养和发展学生思维的广阔性,提高里他们解决问题的应变能力。例如,在教学“工程应用题”时给出这么一道题:“一条水渠3000米,甲队单独修10天完成,乙队单独修15天完成,两队合修几天完成?”这道题解法比较简单,我们所要做的是要引导学生对这道题进行变化。
(一)只改变条件
变化1:一条水渠,甲队单独修10天完成,乙队单独修15天完成,两队合修几天完成?
变化2:一条水渠,甲队单独修10天完成,乙队单独修15天完成,若甲队先修5天,乙队再加入合修还要几天完成?
(二)同时变化条件和问题
变化1:一条水渠,甲队单独修10天完成,乙队单独修15天完成,甲乙两队合修两天后由甲队独修,还需要几天才能完成?
变化2:一条水渠,甲乙合修6天完成如果甲队单独修10天能完成,甲乙两队合修一段时间以后,甲队有别的任务被调走,剩下有乙队独自完成,结果9天就完成甲队修了几天?
通过这样从一个问题变化成若干问题的训练,学生真正收到举一反三、触类旁通的功效。
三、精心设计问题,提高学生提问题的能力
小学生有着丰富的想象力,对新鲜的事或物总想去感知。因此,我们要认真
给学生设计问题,创设问题情景,从而培养并提高学生提问题的能力。
在数学教学中,课堂上的知识传授、信息反馈、数学思维的启发大多通过提
问题的方法来实现。所以,在数学教学课堂里我们要充分利用各个环节,根据学生的特点把握好教学中的重点、难点,去挖掘出能启迪学生的数学思维,开发学生语言的问题情景,激发学生积极作答,从而去启发学生学会提出问题。这样,从让学生回答问题到学会提问题,从而发展了学生的语言和思维。例如:教学分数的基本性质时我们可以提问学生:“看了课本里的分数的基本性质,你们觉得有什么问题需要老师解决呢?”。通过这样的引导,学生可能会提这样的问题,为什么在这句话里要加“都”呢?为什么要加“相同”二字呢?,为什么要“非0的数”?如果分子和分母都加上相同的数,分数的大小会发生变化吗?学生们题这么多的问题后,接着引导学生认真观察课本上的情景图和等式,并要求学生围绕这些问题展开讨论,这样的教学过程,不仅使学生弄清了这些问题,培养了思维能力,而且也提高了学生的提问题的能力。
四、训练思维的灵活性,提高学生的联想能力
要想实现创新,就要能想到别人想不到的问题,解决别人解决不了的问题,而这些问题的产生多数是在平常现象中的,只有善于探索、善于“由此到彼”的人才能达到以上要求,而这种“由此到彼”的联想能力,即为思维的灵活性,即是创造性思维的核心。主要体现在顺向思维、整体思维等方面。
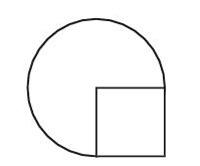
例如,教学“组合图形面积计算”,给出如下的习题:如图,正方形的面积为16平方分米,求圆的面积?
不少学生按照常规思路,想先求出正方形的边长,也就是圆形的边长,再求圆形的面积但是怎样苦思冥想,终究因无法求出正方形的边长而失败,可有的学生却能逆向思维想到正方形的面积就是圆形半径的平方,只要把正方形的面积乘圆周率既是圆形的面积。这样的方法跳出常规的数学思维模式,根据题中隐含的条件应用逆向思维,使解题过程简单、易懂,让创造性思维在解决数学问题中充分体现。
五、培养思维的发散性,提高学生一题多解的能力
创造思维能力以心理学方面分析,是指将集中思维和发散思维进行有效结合,其中,发散思维是关键,所以,在教学过程中,学会利用各种手段培养学生的发散能力,如定期开展课堂讨论,组织一题多问、一题多解等训练方式,不仅对培养创造型人才有重要意义,还可以使学生解题思路开阔,妙法频生。
以上阐述的多种解法,可使学生充分了解、掌握分数应用题的常用方程式,且有助于学生复习之前学习的知识内容,达到一举多得的教学效果。激发了学生思维能力的同时,提高了他们一题多解的能力。
数学思维并不是单一的、独立的,它是一种心理活动,也是各种思维品质的结合体。教师要为学生创造和谐民主的学习环境,通过正确的指导让学生自主活动,可有助于学生各种思维品质的正确、和谐发展,最终实现提高数学课堂效率、学生数学素质的目标。
(责编 赵建荣)
