导体角域静电场问题及其分析
2016-01-14刘煜琛
刘煜琛
摘要:角域导体是指两个半无限大平面沿一定的角度放置,在角域空间中分布有一定的电荷时,求其电场分布,是静电场的基本问题.但是,由于角域导体的角度不同,其分析方法也不一样,而且一不小心就容易出错.本文对导体角域静电场问题进行了分析和总结.
关键词:导体角域;静电场;问题;分析
中图分类号:G633.7 文献标志码:A 文章编号:1674-9324(2016)02-0182-02
一块无限大平面导体沿某一条直线折成一定的角度,角域导体的两个半无限大平面是一个等势面,几何像电荷的空间分布必须满足该边界条件;满足该边界条件的所有点在角域中任一点P的电势即它所满足的拉普拉斯方程的解[1].但是,此求解过程一般不简单,因此,可以用等效方法[1-3],例如镜像法和保角变换法求解某些特殊形状边界区域中的静电场,直观简洁、可避免大量繁冗运算[1-3].但是,鏡像法和保角变换法都有其适用条件,由于角域导体的角度不同,其分析方法也不一样,而且一不小心就容易出错.本文对导体角域静电场问题进行了分析和总结.
一、特殊导体角域内静电场问题求解——镜像法
当电荷分布于角域空间时,因为静电感应,在导体表面上会出现感应电荷,此时,角域空间中任一点的电势和电场强度是原电荷和导体表面的感应电荷产生的电势和场强的叠加.但是,导体表面感应电荷的分布规律一般情况下是很难求出,甚至不能求出的.而对某些具有特殊形状边界条件导体的静电场问题,可用镜像电荷来代替分界面感应电荷所产生的效果,避免了求解感应电荷分布函数的大量繁冗运算,从而使问题的求解大为简化.
当θ=π/n,N∈Z即π/θ为整数时,该角域中的场可以用镜像法求解.
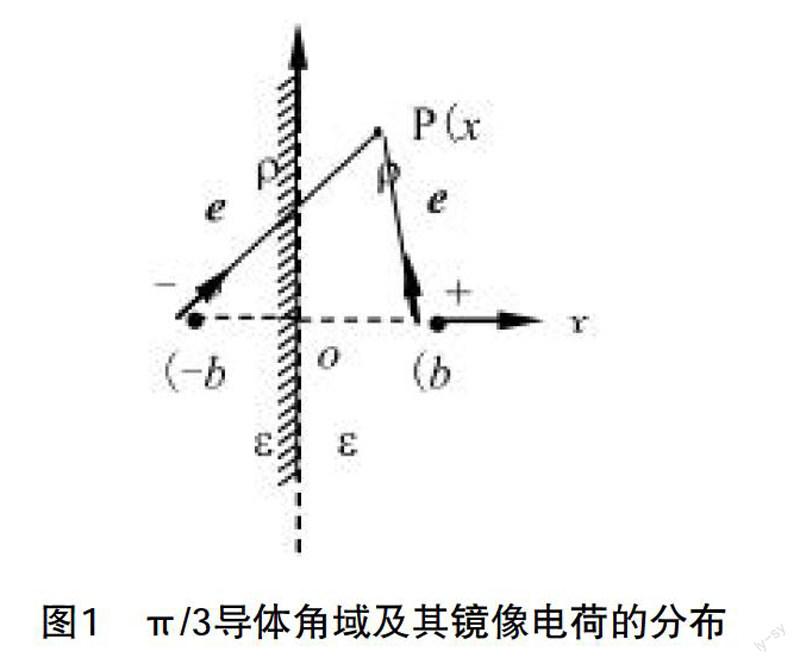
1.特殊导体角域内点电荷的静电问题.设角域导体的夹角为θ,该角域中的电荷有(2n-1)个镜像电荷.
以n=3为例,即角域导体的夹角为π/3,设角域内有一个点电荷q,则角域外有2n-1=5个镜像电荷,大小和位置如图1所示.所有镜像电荷都正、负交替地分布在同一个圆周(圆心为该角域的顶点,半径为该点电荷到顶点的距离)上.
因此,角域内任一点(点电荷q点所在的点除外)的电位φ为6个点电荷产生的电位的叠加.
对于夹角为θ的点电荷导体角域,设点电荷的极坐标位置为((r ,θ )),其镜像电荷有如下特点:
(1)所有的镜像电荷(包括点电荷本身)均匀分布在以角域顶点为圆心、半径为r 的圆上;
(2)任意相邻两个镜像电荷(包括点电荷本身)都是带等量电荷的异号电荷(等值异号),且相互之间以夹角2θ 和2(θ-θ )交替分布.
二、特殊导体角域内线电荷的静电问题
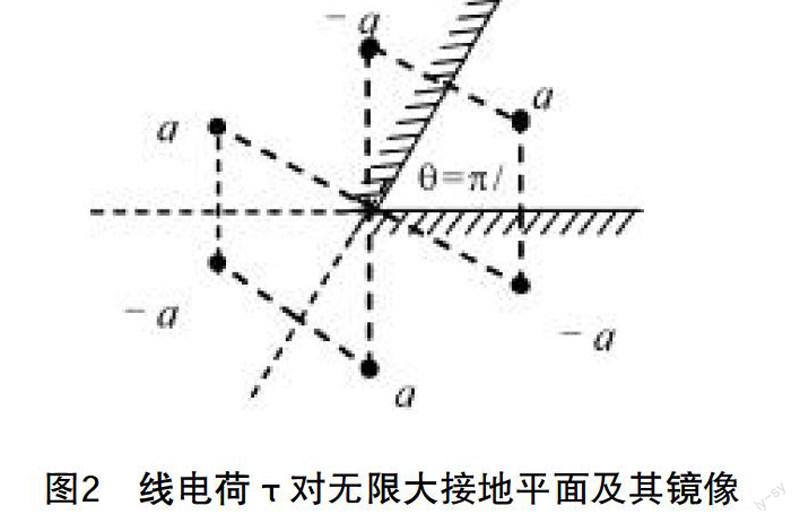
设由两个接地导体平面组成的夹角为θ的角域,有一电荷线密度为τ的无限长直线置于二面角内部,当θ=π/n,N∈Z,即π/θ为整数时,可以用镜像法求解.例如,线电荷τ对无限大接地平面及其镜像电荷如图2所示.
任取Q点为电位参考点,则P点电位为
φ = dρ- dρ
=C+ ln
由于导体平面接地,所以C=0.因此场中任意点p电位为
φ = ln = ln ,但是π/θ,不为整数或者角域夹角为钝角时,镜像法不再适用.采用保角变换法求解.
二、一般导体角域的线电荷静电场问题求解——保角变换法
设接地导体θ角域内置无限长线电荷,为使表达简洁,采用极坐标系.设线电荷τ的极坐标位置为(r ,θ ),做保角变换W=z ,n=π/θ,设变换后的线电荷位置为(ρ ,φ ),有ρ e =(r e )
除Z=0(W=0)点外,保角变换将Z平面上的θ导体角域变为W平面的上半平面,线电荷密度变换后保持不变,其位置为w (r ,nθ )处.因此,其镜像电荷位于W平面的下半平面,位置为w (ρ ,-φ ).故上半平面任意一点w(ρ,φ)的电势为
φ = ln .
还原到Z平面,将变换函数:n=π/θw=(re ) ,w =(r e ) ,w =(r e ) 代入上式中,有
φ = ln .
三、一般导体角域的点电荷静电场问题求解——分离变量法
当点电荷位于任意导体角域时,如果运用保角变换和镜像法求解,过程和第2节类似,有
φ = ( - ).
很显然,上述表达式错误.其原因是保角变换在二维平面静电场问题时确实具有保角性,而三维变换与反演不具保角性.且点电荷明显是三维问题,因此,采用保角变换求解三维点电荷问题会出错.须采用分离变量法[4]进行求解,任意一点p(r,α,z)的电势为φ = φ coskzdk
其中,
φ = K (kr )I (kr)sin(iθ )sin(iθ) rr 式中n=π/θ,k ,I 为柱函数.
参考文献:
[1]王福谦.基于保角映射的镜像法的应用[J].大学物理,2015,34(3):14-16,24.
[2]王福谦.求解静电场边值问题的一种方法[J].大学物理,2013,32(10):24—26.
[3]梁昌洪,陈曦.平面镜像法与有源保角变换[J].电气电子教学学报,2010,32(2):2-5.
[4]尼蒂盒,扎普蒂金.电动力学习题集[M].北京:人民教育出版社,1978:45-46,230-231.
