基于极大似然法的负偏水文序列参数估计方法研究

基于极大似然法的负偏水文序列参数估计方法研究

胡诗松a，陈进a，b，尹正杰a,c

(长江科学院 a.流域水资源与生态环境科学湖北省重点实验室；b.院长办公室；

c.水资源综合利用研究所，武汉430010)

摘要：针对皮尔逊Ⅲ型曲线参数估计方法中尺度参数β>0，无法适用于潮位、水位等负偏水文序列(β<0)参数估计的问题，从正偏序列与负偏序列的关系出发，提出了一种极大似然估计的新方法。该方法是将负偏序列先后转换为正偏序列、伽马分布序列，并利用负偏序列确定ξ初值，通过伽马分布序列迭代计算得到α,β的极大似然估计值。以某潮位站44 a的最高潮位数据为算例，比较了负偏极大似然法、负偏矩法、正偏查表法3种估计方法对负偏序列拟合的精度，结果发现负偏极大似然估计法的3项拟合指标：PPCC检验值为0.993，OLS检验值为0.010，KS检验值为0.052，均优于负偏矩法、正偏查表法。为此，负偏极大似然法对负偏序列拟合的精度为最优。

关键词：水文频率；负偏序列；极大似然估计；皮尔逊Ⅲ型曲线；MATLAB软件

中图分类号：TV12

文献标志码：A

文章编号：1001-5485(2015)06-0116-04

Abstract:The commonly used probability density function of Pearson-III distribution is invalid for negative-skewness water level and tide level series (β<0). To solve this problem, a means of maximum likelihood estimation (MLE) based on the relationship between negative-skewness series and positive-skewness series is proposed. In this method negative-skewnessPearson-Ⅲ distribution is translated into positive-skewnessPearson-Ⅲ and gamma

收稿日期：2015-04-02；修回日期：2015-04-13

作者简介：李凌霄(1991-)，男，湖北武汉人，硕士研究生, 主要从事信息技术开发与应用方面的研究，(电话)18627744329(电子信箱)lukelee0329@gmail.com。

DOI:10.3969/j.issn.1001-5485.2015.06.021

1研究背景

在水文计算中常需推求100 a一遇、甚至1 000 a一遇的设计值，水文频率曲线是合理解决这一问题的有效“工具”。根据《水利水电工程设计洪水计算规范》(SL44—2006)，我国水文频率计算线型采用皮尔逊Ⅲ型曲线。目前常用的皮尔逊Ⅲ型曲线尺度参数β>0，适用于Cs>0的正偏水文序列[1]，但分析水库水位、潮位等水文序列时经常出现负偏的情况，此时如仍沿用上述曲线配线，解得的理论频率曲线和经验点偏离较大。为解决该问题，很多学者进行了相关研究。如蔡体录[2]研究了负偏和正偏频率的关系，提出了一种基于查表的“三点法”；张涛等[3]提出用多项式代替皮尔逊Ⅲ型曲线配线以提高拟合精度；李兴拼等[4]给出了基于矩法的正负偏转换公式；张家鸣等[5]提出了一种直接求解负偏皮尔逊Ⅲ型曲线的方法。

国家标准规定使用其他线型配线需要单独论证，由于多项式法通用性不强，而用矩法直接估计偏态系数Cs抽样误差又太大。因此，针对这2方面的问题，本文从正偏负偏频率曲线的转换关系出发，提出了比矩法精度更高的负偏水文序列皮尔逊Ⅲ型曲线参数估计的极大似然估计方法(后文统一简称为负偏极大似然法)，并以某潮位站44 a的最高潮位数据为算例，比较负偏极大似然法、负偏矩法、正偏查表3种方法对负偏序列拟合的精度，同时，对本文提出的方法加以了分析和验证。

2计算原理

负偏水文序列的皮尔逊Ⅲ型曲线计算主要有2种思路：①寻找正偏负偏序列的关系，把负偏序列计算转化为正偏，然后查表或者用矩法等方法估计参数；②直接根据负偏皮尔逊Ⅲ型曲线密度函数求解，需先计算该密度函数的积分然后用矩法或极大似然等方法估计参数。

皮尔逊Ⅲ型曲线密度函数为

(1)

式中：α为形状参数(α>0 )；β为尺度参数；ξ为位置参数；x是样本值；Γ(α)为α的伽马函数[6]。

当β<0时式(1)为负偏序列对应的皮尔逊Ⅲ型曲线密度函数。采用第1种思路计算时，如果用矩法估计参数，取100个样本点时α的抽样误差为40%～126%之间[1]，序列样本数一般不会超过100，所以实际抽样误差会更大；采用第2种思路计算时，如果用极大似然法估计参数，由于式(1)右边有负数，不能同时对两端取对数，直接进行极大似然估计将十分困难。为了兼顾计算精度和简易性，本文结合了2种思路，采用先把负偏序列转换为正偏序列，再对正偏序列采用极大似然法对P-Ⅲ型曲线密度函数进行估计参数的计算。

2.1负偏与正偏序列频率曲线关系

(2)

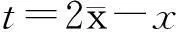
(3)

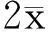
《工程水文学》[1]中给出的正偏皮尔逊Ⅲ型曲线密度函数为

(4)

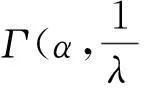
(5)

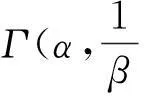
(6)

2.2参数α,β,ξ的极大似然估计

与矩法相比，极大似然估计不仅利用了样本点的信息，还利用了样本分布函数的信息，因此，相较矩法有一定的优势[7]。极大似然估计是用样本在总体中出现几率最大时的参数模拟样本总体参数，对于样本x1,x2,…,xn，设他们的总体密度函数为f(x,α)，则有

(7)

式(7)称为似然函数，使似然函数最大的参数α为样本的极大似然参数估计值。把式(4)代入式(7)就得到了正偏皮尔逊Ⅲ型曲线的似然函数，即

(8)

(9)

把估计出的α，1/β初值代入式(9)就可以解出ξ。具体的转换及迭代求解步骤如下：

(1) 对原始负偏序列x1,x2,…,xn用矩法计算一个ξ的初值ξ1；

(3) 把α1,β1代入式(9)解出ξ2，注意β1与式(9)中的β是互为倒数的关系；

(4) 利用ξ2重复步骤②至③直到相邻2次ξi-ξi-1足够小时停止迭代，最后一次得到的ξi,αi-1,1/βi-1即为所需的极大似然估计值。

3实例应用

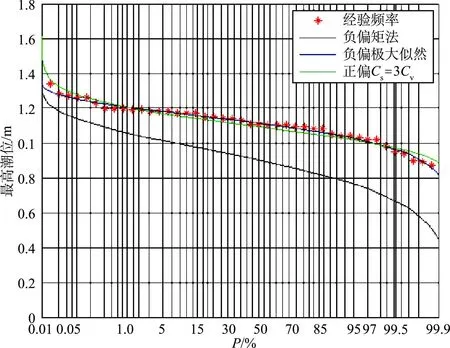
图1　最高潮位频率曲线拟合结果对比 Fig.1　Fitting results of maximum tide level frequency curves

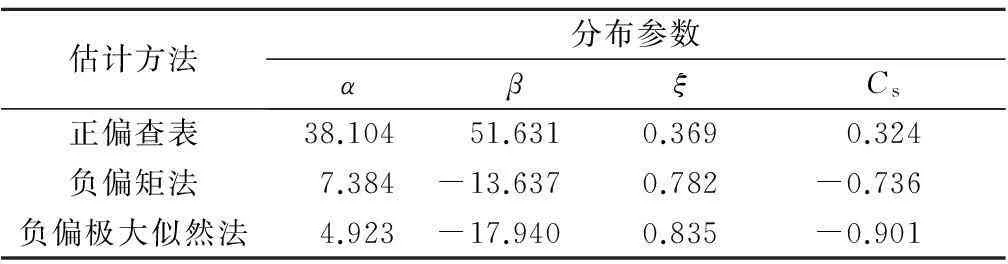
估计方法分布参数αβξCs正偏查表38.10451.6310.3690.324负偏矩法7.384-13.6370.782-0.736负偏极大似然法4.923-17.9400.835-0.901

从图1中可以直观地发现负偏极大似然法和正偏查表2种方法拟合效果较好，正偏查表(取Cs=3Cv)在频率区间两端处有所偏离；负偏矩法拟合效果最差，整个概率区间上偏离经验点距较大。

结合表1分析上述3种估计方法产生不同拟合效果的原因：对负偏水文序列采用正偏查表拟合在频率区间两端处偏离经验点距，是因为我们忽略了样本序列的负偏特性，强制令Cs=3Cv>0，而Cs越大皮尔逊Ⅲ型曲线的上段越陡，下段越平缓[9]；正偏查表和负偏极大似然拟合效果差别不显著是因为本例中Cs=-0.736较小，加上潮位序列本身变化范围很小(0.75~1.34 m)；负偏矩法α=7.384，与负偏极大似然法α=4.923误差达50%，而α是影响皮尔逊Ⅲ型曲线形状的敏感因子，因此， 负偏矩法考虑负偏序列特性拟合效果依然不理想。

为了更加客观地比较3种估计方法的拟合效果，下面分别对3种估计方法进行PPCC(概率点据相关系数)检验[10]、OLS(离差平方和)检验[11]、KS(柯尔莫哥洛夫-斯摩洛夫)检验[12]。这3种检验方法从不同角度描述拟合效果，PPCC检验反映了模拟值和样本值的相关性，数值越大拟合效果越好；OLS检验反映了离差的累积情况，数值越小拟合效果越好；KS检验反映了拟合最差点的离差，数值越小拟合效果越好。3种检验方法的公式及3种估计方法的检验值见表2。

表2拟合优度检验值

Table 2Test values of fitting efficiency

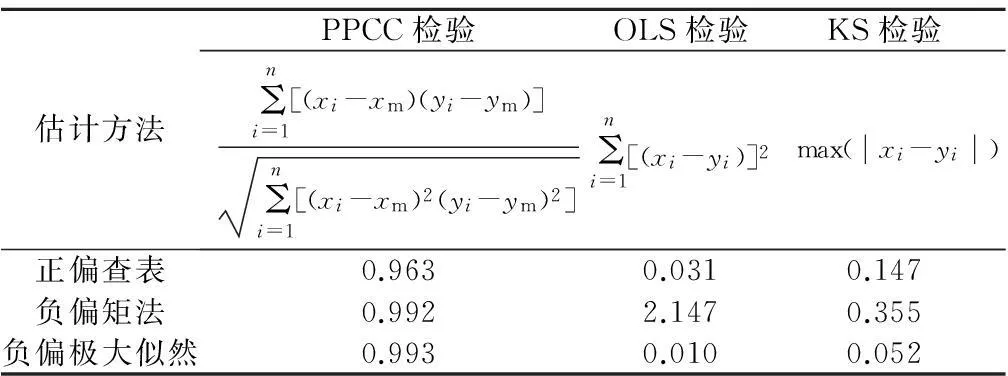
估计方法PPCC检验OLS检验KS检验Σni=1[(xi-xm)(yi-ym)]Σni=1[(xi-xm)2(yi-ym)2]Σni=1[(xi-yi)]2 max(xi-yi)正偏查表0.9630.0310.147负偏矩法0.9922.1470.355负偏极大似然0.9930.0100.052

注:xi,yi分别为同频率对应经验曲线值和拟合曲线值；xm,ym分别为xi,yi均值。

表2结果表明:负偏矩法除了在PPCC检验所得检验值优于正偏查表法外，其他指标均劣于正偏查表法；负偏极大似然法3种检验方法所得检验值都是最优的，拟合度最优；3种估计方法的PPCC检验所得指标都比较好，说明最高潮位曲线采用皮尔逊Ⅲ型曲线作为分布密度函数是符合实际情况的；OLS和KS检验法所得检验指标正偏查表分别是负偏极大似然的3倍和2.7倍，说明本文提出的负偏极大似然法在累积离差和拟合最差点离差方面拟合效果比正偏查表有较大提升。负偏矩法KS检测指标为0.355已经超过了《水文情报预报规范》(GB/T22482—2008)潮位的误差限，因此不能直接使用该方法的计算结果。

4结论

正偏查表法估计负偏序列在频率区间两端处拟合效果较差，无论正偏负偏序列用矩法估计参数Cs都是无效的。本文基于先把负偏序列转换为正偏序列，再用极大似然法对转化后的正偏序列进行P-Ⅲ型曲线密度函数参数估计的计算思路，提出了一种新的极大似然迭代求解方法，并经过了某潮位站44 a的最高潮位数据验证。所提出的负偏极大似然估计法3项拟合指标：PPCC检验值为0.993，OLS检验值为0.010，KS检验值为0.052，均优于负偏矩法、正偏查表法。为此，负偏极大似然法对负偏序列拟合的精度为最优。

建议采用皮尔逊Ⅲ型曲线估计水文系列时应先判断该水文系列是正偏还是负偏，如果是负偏系列，应转化为对应的正偏系列后采用极大似然估计密度函数参数，这既可以提高频率分布曲线估计的精度也便于使用计算机自动化计算。

参考文献：

[1]詹道江，徐向阳，陈元芳.工程水文学[M]. 北京：中国水利水电出版社，2010. (ZHAN Dao-jiang, XU Xiang-yang, CHEN Yuan-fang. Engineering Hydrology[M]. Beijing: China Water Power Press, 2010. (in Chinese))

[2]蔡体录. 负偏频率曲线的计算[J]. 东海海洋,1983,1(4):1-7.(CAI Ti-lu. Calculation of Negative Deviation Distribution Frequency[J]. Donghai Marine Science, 1983, 1(4): 1-7. (in Chinese))

[3]张涛,王世勋,王祥三，等. 水位负偏分布频率计算方法分析与研究[J].水文,2008,28(2):5-9. (ZHANG Tao, WANG Shi-xun, WANG Xiang-san,etal. Analysis of Negative Deviation Distribution Frequency for Water Stage Calculation[J]. Journal of China Hydrology, 2008,28(2):5-9.(in Chinese))

[4]李兴拼,郑江丽. 浅论P-Ⅲ型负偏频率曲线计算方法[J]. 广东水利水电, 2010, 9(9): 17-18. (LI Xing-pin, ZHENG Jiang-li. Calculation Method of Negative-skewness Series with Pearson-Ⅲ Frequency Curve[J]. Guangdong Water Resources and Hydropower, 2010, 9(9): 17-18. (in Chinese))

[5]张家鸣,陈晓宏,叶长青. Pearson-Ⅲ型频率曲线对负偏水文序列的计算[J]. 水利学报,2012, 43(11):1296- 1301. (ZHANG Jia-ming, CHEN Xiao-hong, YE Chang-qing. Calculation of Negative-skewness Hydrological Series with Pearson-Ⅲ Frequency Curve[J]. Journal of Hydraulic Engineering, 2012, 43(11): 1296-1301. (in Chinese))

[6]STEDINGER J R, VOGEL R M, FOUFOULA-GEORGIOU E. Handbook of Hydrology. New York: McGraw-Hill, 1993.

[7]余泱悦,贺信. P-Ⅲ曲线的极大似然估计及应用[J]. 人民长江, 2012, 43(21): 21-23. (YU Yang-yue, HE Xin. Maximum Likelihood Estimation of Pearson-Ⅲ Curve and Its Application[J]. Yangtze River, 2012, 43(21): 21-23. (in Chinese))

[8]PONCE V M. Engineering Hydrology[M]. New Jersey: Englewood Cliffs, 1989: 214-216.

[9]RAO A R, HAMED K H. Flood Frequency Analysis[M]. Boca Raton: CRC Press, 2000.

[10]涂新军,陈晓宏. 基于PPCC检验法的枯水径流概率分布选型研究[J]. 水电能源科学,2006,24(1):76-79. (TU Xin-jun, CHEN Xiao-hong. Study on Probability Distribution of Low Flow Based on PPCC Method[J].Water Resources and Power, 2006,24(1):76-79. (in Chinese))

[11]成静清. 非一致性年径流序列频率分析计算[D].陕西：西北农林科技大学,2010. (CHENG Jing-qing. Hydrological Frequency Calculation Principle of Inconsistent Annual Runoff Series[D]. Shaanxi: Northwest A& F University, 2010. (in Chinese))

[12]郭生练. 设计洪水研究进展与评价[M]. 北京：中国水利水电出版社，2005. (GUO Sheng-lian. Advance and Assessment of Design Flood Hydrograph Methods[M]. Beijing: China Water Power Press, 2005. (in Chinese))

(编辑：陈绍选)

Maximum Likelihood Estimation of Negative-skewnessHydrological Series

HU Shi-song1,CHEN Jin1,2,YIN Zheng-jie1,3

(1.Key Lab of Basin Water Resource and Eco-environmental Science in Hubei Province,

Yangtze River Scientific Research Institute, Wuhan 430010, China; 2.Administration Office,

Yangtze River Scientific Research Institute, Wuhan430010, China; 3.Water Resources Department,

Yangtze River Scientific Research Institute, Wuhan430010, China)

distribution in sequence. The initial value ofξis decided by the negative-skewness distribution and the MLE ofαandβare calculated through the gamma distribution. In the iterative process the sampling error with evaluating coefficient of skewness will be avoided. Moreover, the 44-year record of maximum tide level at a tide station is used as calculation example. The fitting accuracy of negative-skewness MLE, negative-skewness moment method and positive-skewness table look-up are compared. The fitting results of negative-skewness MLE (test value of PPCC is 0.993, OLS 0.010, and KS 0.052) are superior to those of the other two methods. In conclusion, negative-skewness MLE has the optimum fitting accuracy for negative-skewness hydrological series.

Key words: hydrological frequency; negative-skewness series; MLE; Pearson-Ⅲ frequency curve; MATLAB software

欢 迎 订 阅欢 迎 投 稿

2015,32(06):120-126