基于流形学习的阔叶树叶面积指数的研究

2016-01-12薛联凤,云挺,罗毅等

森林工程 2015年2期

关键词：降维

基于流形学习的阔叶树叶面积指数的研究

薛联凤，云挺，罗毅，姚志安

(南京林业大学信息学院，南京 210037)

摘要：叶面积指数(LAI)是一个量化植物绿色指数的重要参数之一。精确测量叶面积指数对研究生态系统的功能结构特性具有重要的意义。植物生存环境影响植物叶子的形态，叶舒展、卷曲、病虫害引起缺损等几何形态的变化，对于测量带来很大不便。本论文鉴于在传统的叶面积指数的测量方法存在许多弊端，借助于流形学习方法，将三维数据降为二维数据，在二维空间进行数据的精确测量，得到相当准确的叶面积指数，从而获得植物精确的参数有了一定科学依据。

关键词：叶面积指数；流形学习；降维

中图分类号：S 718.4；TP 301.6

文献标识码：A

文章编号：1001-005X(2015)02-0075-06

Abstract：Leaf area index(LAI)is one of the important parameters for green rating.The precise measurement of LAI has great significance to study the functional structure characteristics of ecosystems.The living environment can affect the form of leafs and the leaf stretch，curly，plant diseases and insect pests also cause the change of leaf form，which is not convenient to the measurement of leafs.In this paper，in consideration of the drawbacks of traditional measurement methods of leaf area index，the mani-fold learning method was used to reduce the three-dimensional data to two-dimensional data and realize precise measurement.In this way，a fairly accurate LAI can be obtained，which provides scientific basis for the accurate measurement of the parameter.

Keywords：leaf area index；mani-fold learning；dimension reduction

收稿日期：2014-10-20

基金项目：国家自然科学基金(31300472)；江苏省自然科学基金(BK2012418)；2014江苏省社会发展项目基金资助(SBE2014070966)

作者简介：第一薛联凤，硕士，副教授。研究方向：图像处理。E-mail：285201972@qq.com

Study of Broad-leaved Trees LAI Based on Mani-fold Learning

Xue Lianfeng，Yun Ting，Luo Yi，Yao Zhian

(College of Informaiton，Nanjing Forestry University，Nanjing 210037)

引文格式：薛联凤，云挺，罗毅，等.基于流形学习的阔叶树叶面积指数的研究[J].森林工程，2015，31(2)：75-80.

目前，人们对地球居住的生存环境的优良指数要求越来越高，在有限地球绿化面积范围内提高优化指数，对于植物种植种类，以及植物性能改变，都会直接影响人类的生存优良指数[1-4]。其中叶面积指数(LAI)是研究植物的林分重要参数，是描述森林冠层结构特征的重要因子之一，是植物冠层空隙的动态、平衡的认识和掌握的重要指标。叶面积指数在植物生长模型、气候模型、能量平衡模型和冠层反射模型等都有着重要作用，叶面积指数控制着植被冠层的多种生物物理和生理过程[5-9]。精确测量叶面积指数是一个森林绿化评价指标，也是对研究生态系统的结构和功能结构特性具有重要的意义[10-14]。

在测量LAI时要受到其定义、采样方法、数据分析和仪器误差等多种因素影响，植物生存状态也都会影响植物叶子的形态，许多植物的叶子，在阳光和水分充足时，树叶舒展，但是随着季节变换，由于气候下降和水分的流失会发生向内卷曲等几何形态的变化，对于测量带来很大不便。国内外至今没有通用而简便的方法，国内外学者对各种测量方法进行了长期大量的研究[15-20]。由于传统测量方法对植物本身具有一定破坏性，即必须人工采集叶子样品，且耗时耗力，很难扩大研究范围，所以一般都采用光学仪器测量的方法。利用光学仪器测得的LAI虽然方便、快速，但数值上比真实的LAI要小。流形学习的方法可以克服这种叶脉内部平整的情况，使高维数据降为低维数据，可以精确测量树叶面积。

流形学习是一种有效的数据降维的处理算法，可以从原始高维采样数据中把低维流形结构恢复出来，即找出高维空间中嵌入的低维流形，实现数据的可视化或维数的约简，并构造出对应的映射。具体到图像数据，就是找出隐藏在由原始图像数据张成的高维空间中的低维结构，挖掘出隐藏在其中的内在规律与本征信息。本论文依据流形学习方法，来测试叶面积指数的，将叶子从复杂的植物图像提取出来。实验结果表明该方法不仅提高了叶子的识别速度，而且具有较为准确的测量数据。

1阔叶树中的流形学习

激光点云数据量大、分布离散，且单点信息量小，因此要尽可能挖掘其中的结构信息(如邻域信息、流形结构等)，而此类信息结构的描述也是一个难点。本文从以下几个方面考虑在原始点云数据中如何流形结构提取有用叶子信息。流形学习是一种有效的数据降维的处理算法，早在20年前seung和Lee就已经在《科学》发表的文章提到流形学习方法理念，并在论文中提到感知以流形的方式存在，并通过实验证明了人脑中的确存在着稳态的流形。在统计模式识别让人类感知过程中架起了一座桥梁，使流形学习具有了更加坚实的理论与实验基础。当前典型的流形学习方法有等度同构映射(Isomap)局部线性嵌入(LLE)、拉普拉斯特征映射(LaP1acianEigemap)、扩散映射，局部切空间标定等。这些流形学习方法能保持原始数据的局部几何结构，从而获得非常好的低维可视化效果，从根本上提升了人们感知高维数据的能力。

本文考虑使用流形学习的方法，即流形局部切空间来构造点云邻域信息。

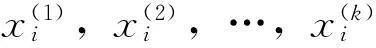
(1)

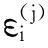
(2)

(3)

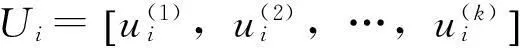
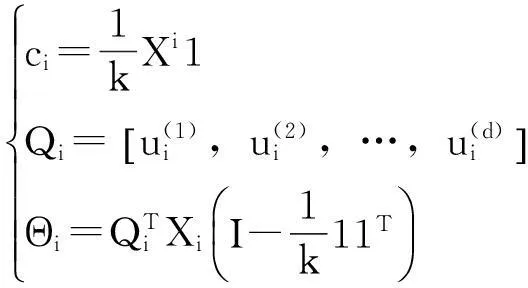
(4)

图1　局部切空间示意图 Fig.1 Schematic of local tangent space

如图1所示，图中平面上红色星点表示样本点xi，蓝色点表示样本点xi的Nk(此图取k=50)，平面(ci,Qi)为点xi的三维局部切平面，高维流形对应的是局部切空间。

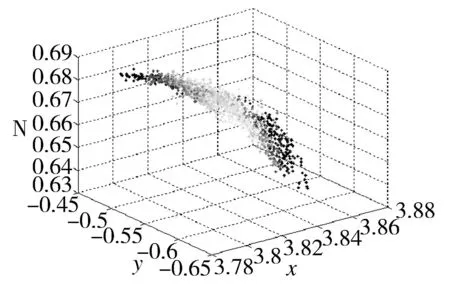
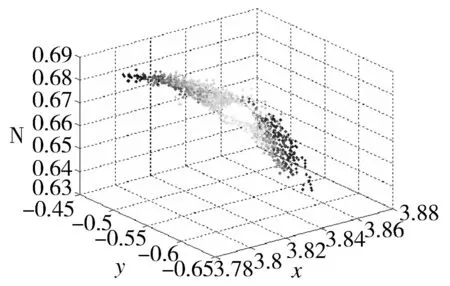
以上介绍了单点的切空间。而同一叶面上不同单点的局部切平面具有连贯性，如图2所示，如此，一片叶面就可以通过一系列局部切平面进行描述。

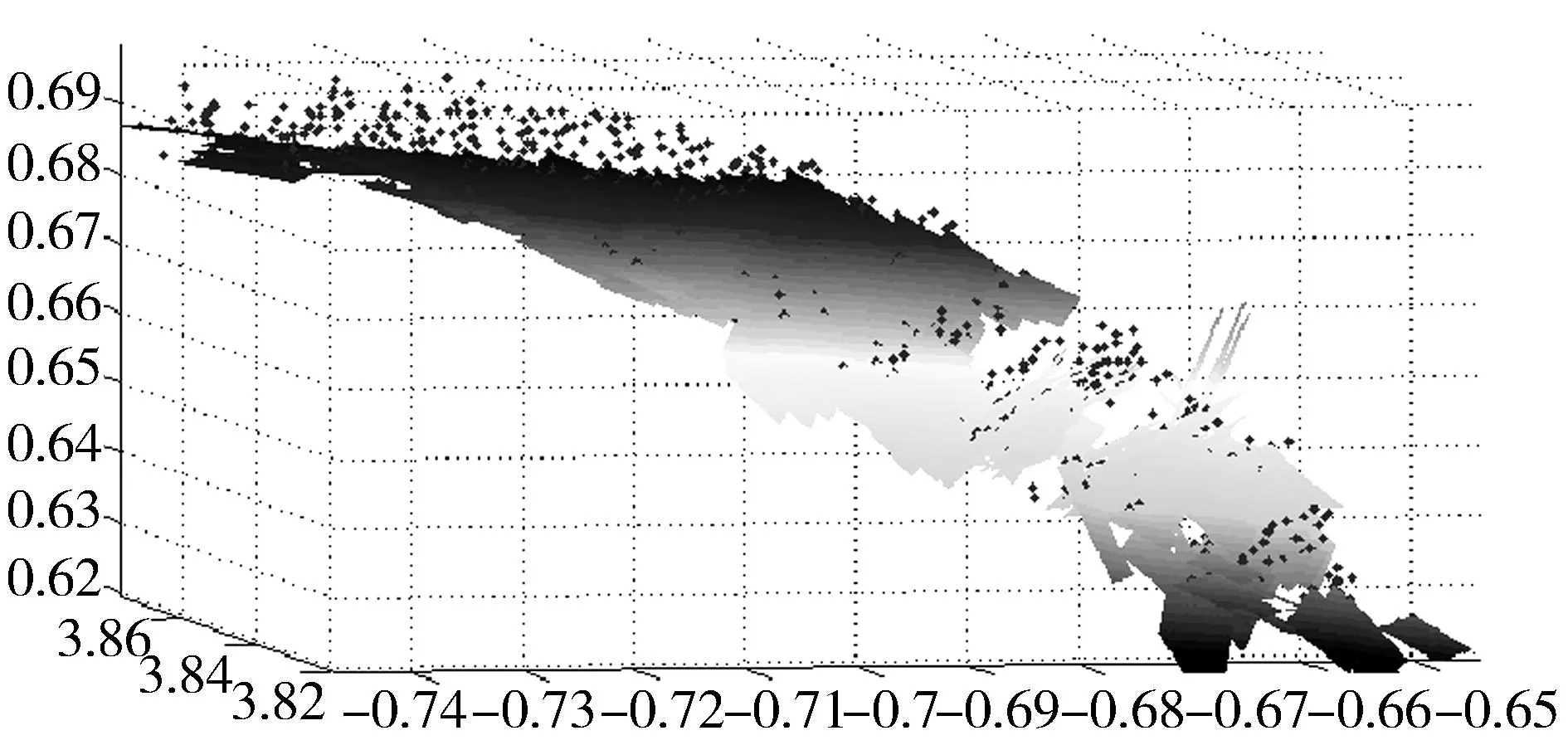
图2　叶面局部切平面 Fig.2 Local tangent plane of the leaf

1.1　流形学习的概念

陈维恒对流形学习的定义是：设X是一个hansdorff空间，若对任意一点χ∈X，都有χ在X中的一个领域U同胚于d维欧氏空间Rd的一个开集。则称X是一个d维流形(或者拓扑流形)。

流形：设M是一个Hausdorff空间拓扑空间，若对每一点P∈M，都有P的一个开邻域U，它与Rd的某个子集同胚，则称M为d维拓扑流形，简称为d维流形。

切向量和切空间：光滑流形M在点x的切向量就是一个映射vxi：C∞→R，且对∀g,h∈C∞(M),a,b∈R，满足：

(1)vx(ag+bh)=avx(g)+bvx(h)。

(2)vx(gh)=vx(g)h+gx(h)。

假设(U,φ)，为点x的一个局部坐标系，则映射

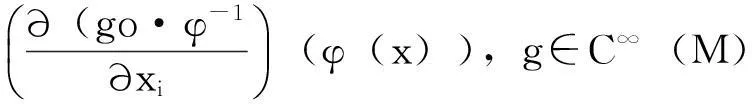
上面为x点的一个切向量。光滑流形的切向量是曲线的切向量的一种推广。xi点的切向量全体记为Π(M)，它是一个实线性空间，称之为M在点x的切空间。

黎曼流形：在光滑流形M的每个切空间Π(M)中都给定了内积，则称M为黎曼流形。

测地距离：设p、q是黎曼流形M中任何两点，则这两点间的测地距离dM(p,q)为M中连接p和q的所有分段光滑曲线的弧长的上下界。

等距流形：设M为d维的黎曼流形，若存在光滑映射g:M→Rd满足：

(1)g:M→g为同胚；

(2)对任意的p,q∈M，有dM(p,q)=‖g(p)-g(q)‖

则称M为d维的等距流形。

1.2　流形学习方法的统一框架

目前流形学习的方法很多，具体方法都由各自处理图像的特点，基本步骤首先在原始输入空间为每个点构建邻域，其次对邻域构建矩阵M，最后对矩阵M进行谱分解，获得低维嵌入结果。这些算法之间的不同之处只是在于收集的邻域的局部信息不同，并且如何利用这些收集的信息来构造全局的嵌入。比如，Iosmap利用每个邻域的邻域点之间的联系和欧氏距离在数据点上构造出一个图，并根据图距离来估计出所有数据点之间的测地距离。构造出的全局低维坐标需要保持估计的测地距离。LLE，HLLE找出每个点同它的邻域点之间的一个线性组合关系，并且由此决定保持这种线性组合结构的低维嵌入。TLSA将每个点的邻域点投影到它在流形上的局部切空间上，然后排列所有的局部坐标来决定低维的全局坐标。

而经典的降维方法如PCA、MDS、LDA等都是通过寻找最优投影子空间来实现降维，而流形学习则假设高维数据分布在低维流形上，目的是恢复数据内在的非线性低维流形结构。

它们的共同优势在于：它们都是非参数的方法，不需要对流形的很多的参数假设；都基于流形的内在几何结构，更能体现现实中数据的本质；它们的求解简单，都转化为求解特征值问题，而不需要用迭代算法，并且避免了局部极值问题。

2树冠的叶片面处理

植物生存环境，都会影响植物叶子的形态，许多植物的叶子，在阳光和水分充足时，树叶舒展，但是随着季节变换，由于气候下降和水分的流失会发生向内卷曲等几何形态的变化，根据函数f(s,t)=[scos,t,ssin(s)]等处理来模拟植物叶子在不同生存环境中，因为外界影响而出现卷曲、缺损和扭曲等现象。人类视觉感知的植物叶子图像在光照和形状变化的情况，都有高维图像空间形成低维流形。在很多实际图像中，都将面临不完整具有缺失观察属性的数据。然而针对具有缺失值得数据集数据，如何快速有效地恢复数据集的内在流形结构。

在图3研究的技术线路图，在一个树枝采取一个树叶进行变形处理，模拟现实的生长状态，对各种变形树叶进行流形学习处理。

图3　局部树冠以及提取树叶变形处理图 Fig.3 Local crown and processed image with leaf deformation extraction

在树枝上提取一个叶子如图4中(b)，树叶利用函数进行变形处理分别得到图4中(c)(d)(e)(f)四幅已经变形的叶片，为了鉴别流形学习方法处理变形叶子优缺点，选取图中一个变形叶片作为一个测试对象，进行下面实验。

3实验结果

实验1，首先利用经典的swiss roll的样图，如图5所示。利用8种流形学习方法处理，比较各种方法优缺点。

实验2：在swiss roll 图中，有意处理一个空洞分别在不同方法来测试，测试各种流形学习处理结果，如图6所示。

实验3：在测量树冠的采集阳光，以及叶面积指数时，树叶卷曲破损，都影响采集计算精确度，利用流形学习，降维处理克服以上问题的缺点。现在利用传统流形学习方法处理，再在实际树木叶子测试，测试结果如图7所示。

在同一树木采取不同树叶，分别进行处理，在各种处理结果中，可以看到各种算法的处理效果图，如图7所示。同时统计各个算法的降维面积，各种算法处理的面积见表1。

(a)树冠一部分

(b)提取一片叶子

(c)函数处理变形叶子1

(d)函数处理变形叶子2

(e)函数处理变形叶子3

(f)函数处理变形叶子4

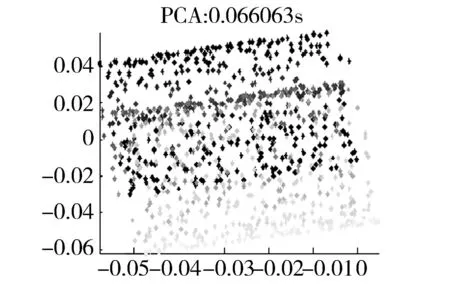
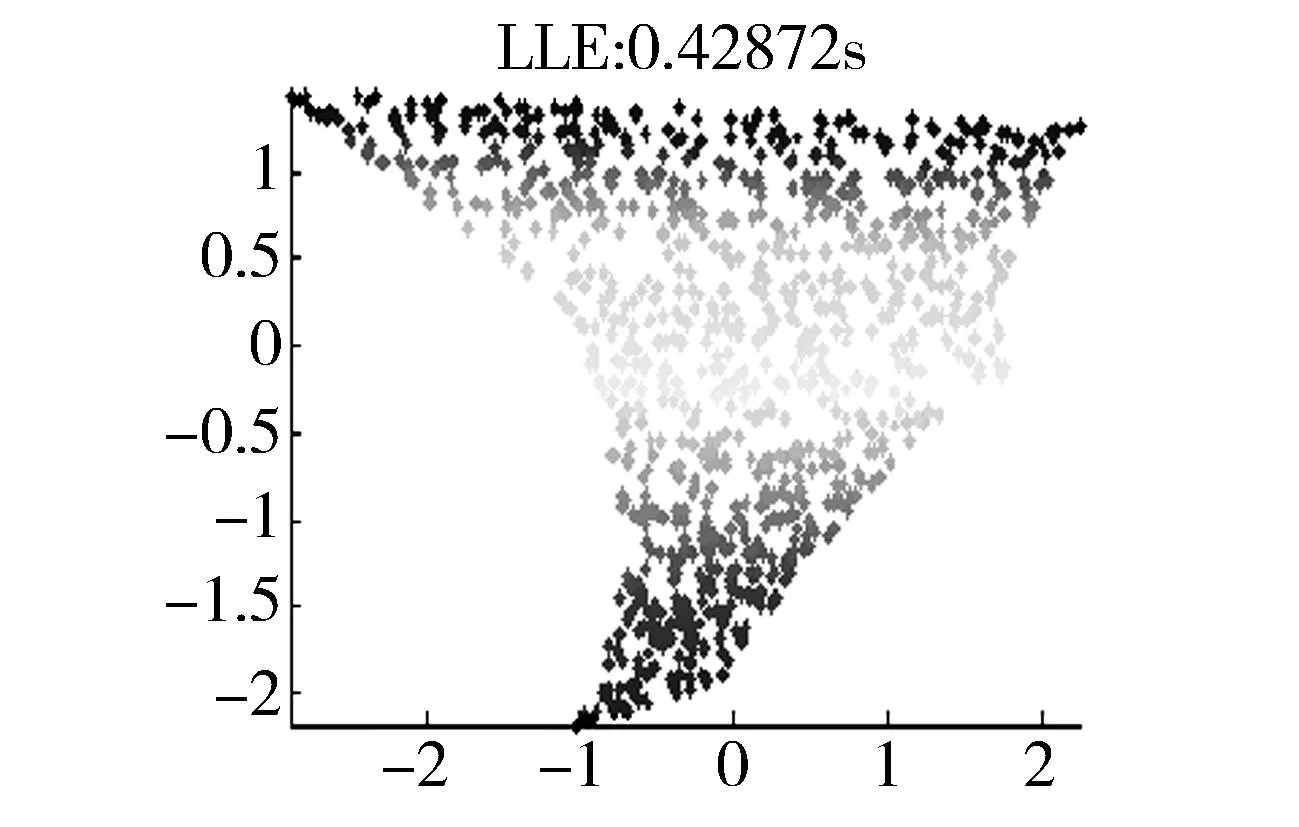
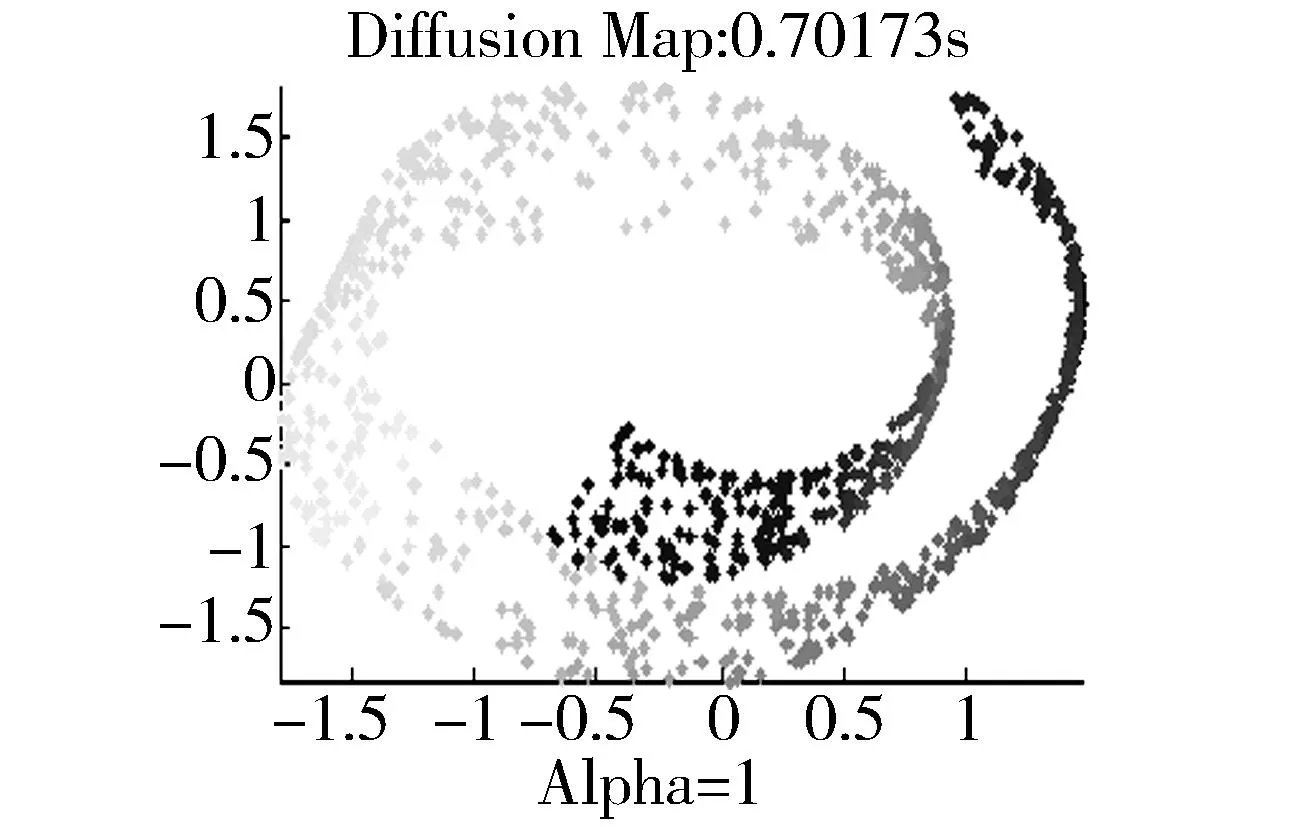
图5　swiss roll 在不同流形学习算法处理的效果图 Fig.5 Effect of swiss roll with different mani-fold learning algorithms

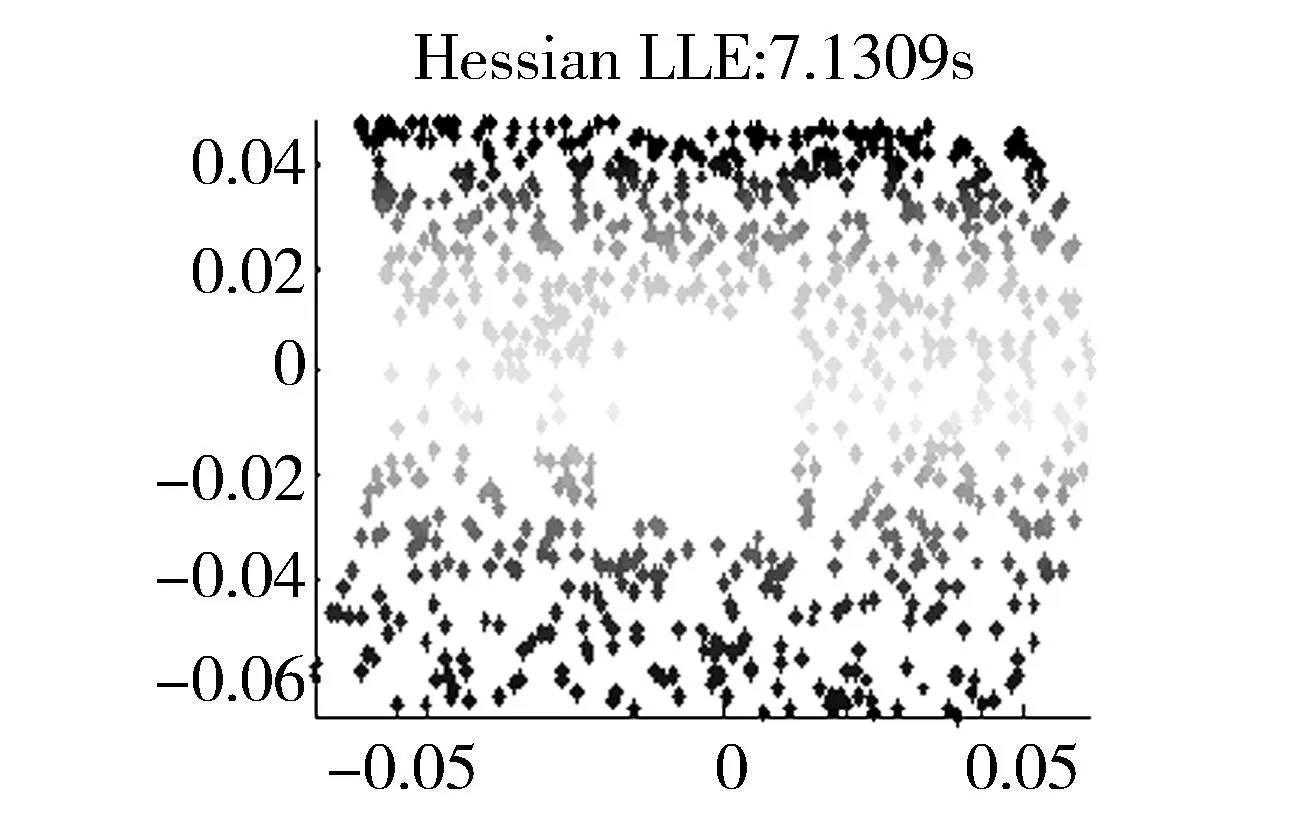
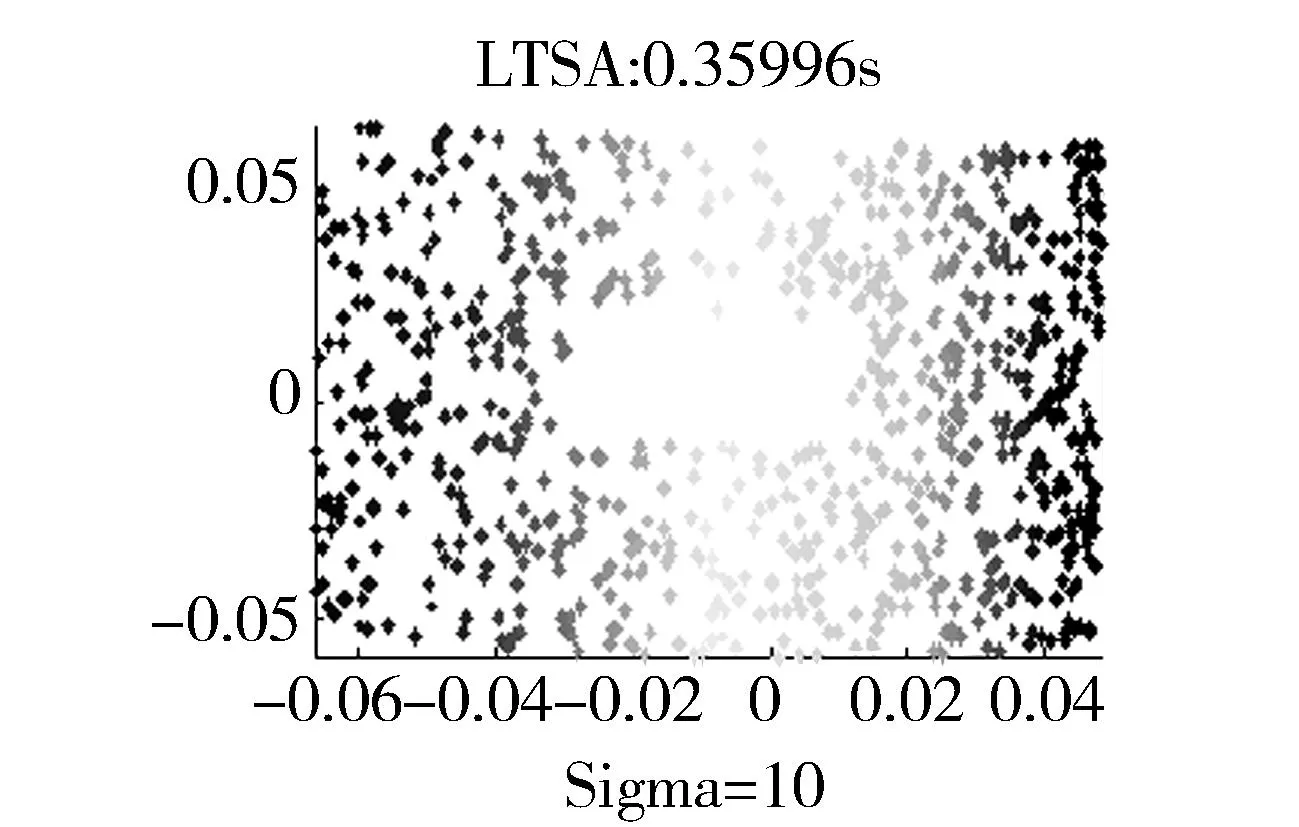
图6　swissholl在不同流形学习算法处理的效果图 Fig.6 Effect of swissholl with different mani-fold learning algorithms

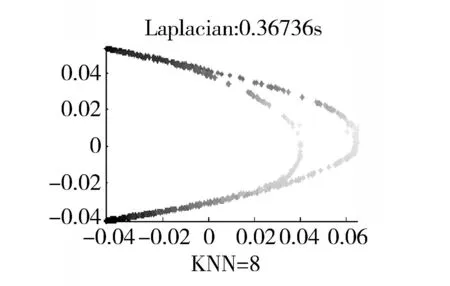
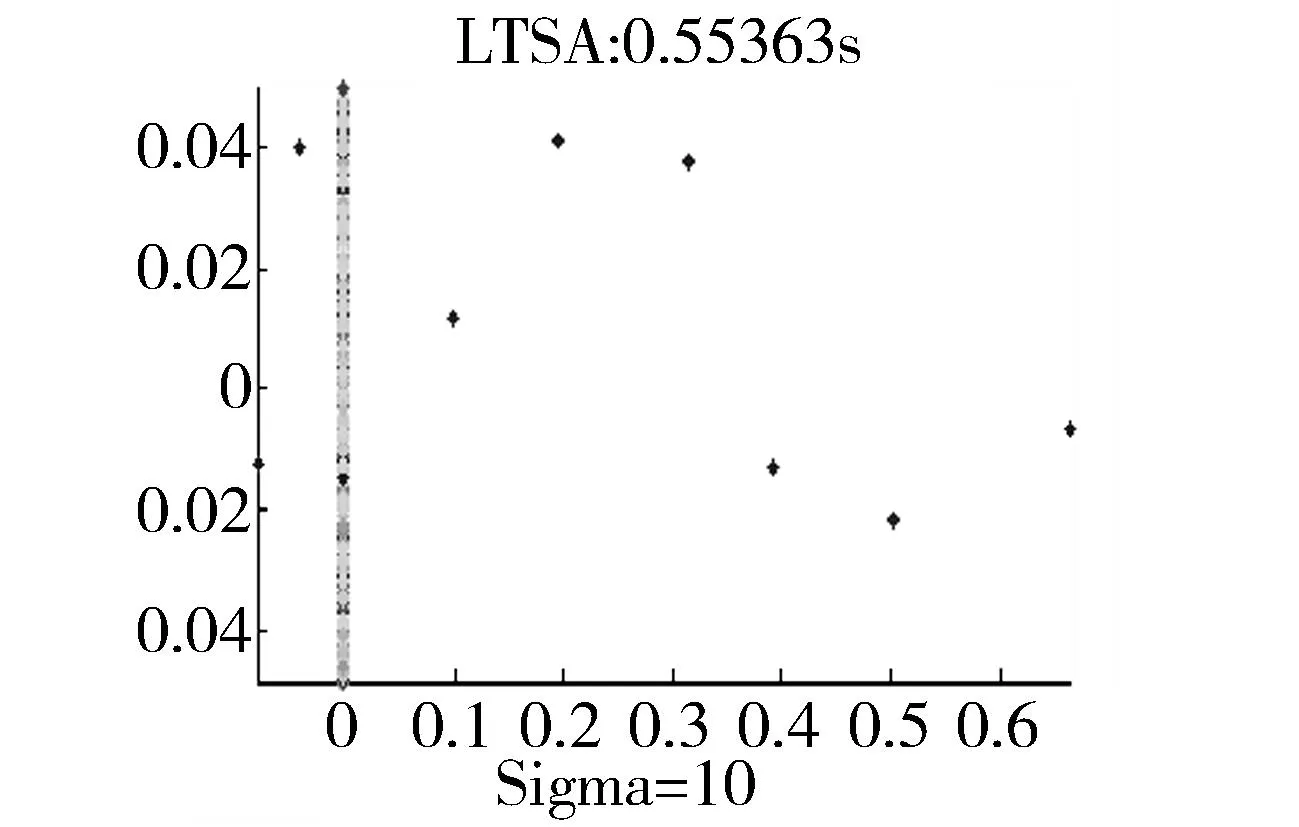
图7　变形树叶在不同流形学习算法处理的效果图 Fig.7 Effect of leafs with deformation by different mani-fold learning algorithms

方法降维后面积(像素个数)瑞士卷有洞瑞士卷折平面高斯模型叶子1叶子2叶子3叶子4多维尺度变换(MDS)6256256256.250.00648000.0060.006主成分分析(PCA)0.0060.0070.0050.0040.00040.0030.00040.0004等距映射(ISOMAP)18000.00590040.00564000.0050.006局部线形嵌入(LLE)96991661612Hession局部线形嵌入(HessionLLE)0.150.010.010.010.0060.00590.06拉普拉斯(Laplacaian)0.0080.010.0060.010.0060.060.0060.06扩散映射(DiffasionMap)12121691691616局部切空间排列(LTSA)0.0150.010.01440.00640.480.00360.0480.008

图8　流形学习降维后面积 Fig.8 Results of image area after mani-fold learning

根据表1所数据，利用图8分析处理的面积值的关系，从处理图像看，可以看到集中处理数据区，比较有规律，通过不同算法，综合考虑得到面积均等，用来计算叶面积指数。

4结论

流形学习方法能有效测试非线性高维数据，并且保留这些结构的特色，生物结果多样，生存形式的多样化，都需要处理降维，准确测量，在本文中，针对函数处理的各种叶子，利用流形学习处理数据高维，使各种变形树叶在不同流形学习方法处理中，获得降维后的树叶的平面图像，并且测得准确的叶面积指数，避免高维数据测量时数据误差。流形学习理论和方法作为一种新型高效的数据分析和处理工具，为植物研究者“不分时间和地域，可以有效地利用数据和信息”提供了解决方案。

【参考文献】

[1]詹宇斌，殷建平，刘新旺，等.流形学习中基于局部线性结构的自适应邻域选择[J]，计算机研究与发展，2011，48(4)：576-583.

[2]侯臣平，吴翊，易东云，等.新的流形学习方法统一框架及改进的拉普拉斯特征映射方法[J]，计算机研究与发展，2009，46(4)：676-682.

[3]Zhang P，Ren Y，Zhang B.A new embedding quality assessment method for manifold learning[J].Neurocomputing，2012，97：251-266.

[4]文贵华，江丽君，文军，等.局部测地距离估计的 Hessian局部线性嵌入[J]，智能系统学报，2008，5(3)：100-103.

[5]Raducanu B，Dornaika F.A supervised non-linear dimensionality reduction approach for manifold learning[J].Pattern Recognition，2008，45：2432-2444.

[6]Fu H，Au O K，Tai C.Effective derivation of similarity transformations for implicit laplacianMesh editing[J].2003，22(13)：1-12.

[7]Wachinger C，Yigitsoy M，Rijkhorst E，et al.Manifold learning for image-based breathing gating in ultrasound and MRI[J].Medical Image Analysis，2011，16(4)：806-818.

[8]Han Y，Xu Z，Ma Z，et al.Image classification with manifold learning for out-of-sample data[J].Signal Processing，2012，5(3)：100-103.

[9]方秀琴，张万昌.叶面积指数(LAI)的遥感定量方法综述[J].国土资源遥感，2003，57(3)：58-62.

[10]任承辉，陈辉，周丽华，等.尤溪县楠木林叶面积指数的研究[J].福建林学院学报，2008，10(1)：68-71.

[11]刘建伟，刘雅荣，朱春全，等.杨树不同无性系叶面积模型的选择及其建立[J].林业科学，1994，30(6)：481-485.

[12]刘铁梅，曹卫星，罗卫红，等.小麦叶面积指数的模拟模型研究[J].麦类作物学报，2001，21(2)：38-41.

[13]张佳华，符淙斌，延晓冬，等.全球植被叶面积指数对温度和降水的响应研究[J].地球物理学报，2002，45(5)：631-637.

[14]周宇宇，唐世浩，朱启疆，等.长白山自然保护区叶面积指数测量及其结果[J].资源科学，2003，25(5)：38-42.

[15]梁达丽，黄克福.台湾桂竹叶面积指数与生物量关系的研究[J].竹子研究汇刊，1994，13(1)：42-46.1994.

[16]彭少麟，张祝平.鼎湖山森林植被优势种云南银柴和柏拉木的生物量及第一性生产力研究[J].应用生态学报，1992，3(3)：202-206.

[17]惠凤鸣，田庆久，金震宇，等.植被指数与叶面积指数关系研究及定量化分析[J].遥感信息，2003：10-13.

[18]王勇.基于流形学习的分类与聚类方法及其应用研究[D].北京：国防科学技术大学，2011.

[19]王婧.流形学习理论和方法研究[D].杭州：浙江大学，2006.