例谈化归思想在物理解题过程中的运用
2016-01-12施亚明
例谈化归思想在物理解题过程中的运用
施亚明
(苏州市第三中学江苏 苏州215000)
搞 要:讨论了运用化归思想解决问题的过程,并举隅说明了化归思想的实际运用.
关键词:化归思想运用过程举隅
1对化归思想的认识
化归思想是数学中解决问题常用的思想方法之一,但化归思想并非源于数学,而是源于人类的思维定势——以现有的方法去解决新的问题.化归即转化和归结,化归思想是指将待解决的问题,通过某种转化手段,归结为另一个容易解决或己经解决的问题,从而解决原问题的一种理性认识.化归思想的核心是“变”字,符合中学生的思维能力及认知特点,易于理解和掌握.
在学习“新知识”的过程中,以化归思想为指导,结合认知同化理论,根据原认知结构中已掌握的旧知识与新知识之间的逻辑关系,通过“同化”或“顺应”作用方式,把原认知结构主动地与新知识相互作用,将新知识转化纳入原有认知结构,形成新的认知结构.
2运用化归思想解决问题的过程
运用化归思想解决问题的过程如图1所示,表现为不是对原问题进行直接求解,而是将待解决问题A转换为相对于求解者来说能够解决的B问题.

图1 化归思想解决问题的过程
在同一个问题序列中,不是由旧问题的求解逻辑演进到新问题的求解,而是从新问题出发,逆向转换,寻求与旧问题连接的通路.其中,问题的转换是化归的关键,只要沟通待解决问题A与已解决问题B之间的桥梁,问题即解决,解决过程体现了化归思想的转换性、间接性、后瞻性、简捷性等基本特征.
学生的物理认知结构中存在着“已解问题网”和“已知结论链”等,这些既是解决问题能力高低的关键要素之一,也是实现化归思想运用的关键环节.学生在问题解决实际操作过程中,只需将待解决问题转化为“网”“链”中的某一环节.由于“网”“链”是动态的,每向“网”“链”上化归一个新的问题,“网”“链”便不断拓展,同时优化“网”“链”结构,使其功能得到加强.
3化归思想的实践运用举隅
在物理教学中,化归思想蕴含在物理概念、定义、定理、定律及公式等之中,物理解题亦是培养学生化归思想的途径之一,此处仅探讨解题过程中的化归思想运用.
3.1审题过程中通过语义转换实现化归
解题活动中,首先是解题情境的辨认,在头脑中建立题目结构的表征,这种情境辨认过程即“审题”.审题的核心过程是“通过语义转换实现化归”,即实现由题目文字(符号)表述到题目物理条件和问题的转化.譬如2013年高考山东卷第23题.
【题目】如图2所示,在坐标系xOy的第一、第三象限内存在相同的匀强磁场,磁场方向垂直于xOy面向里;第四象限内有沿y轴正方向的匀强电场,电场强度大小为E. 一质量为m,带电荷量为+q的粒子自y轴的P点沿x轴正方向射入第四象限,经x轴上的Q点进入第一象限,随即撤去电场,以后仅保留磁场.已知OP=d,OQ=2d,不计粒子重力.

图2
(1)求粒子过Q点时速度的大小和方向;
(2)若磁感应强度的大小为一定值B0,粒子将以垂直y轴的方向进入第二象限,求B0;
(3)若磁感应强度的大小为另一确定值,经过一段时间后粒子将再次经过Q点,且速度与第一次过Q点时相同,求该粒子相邻两次经过Q点所用的时间.
审题通过语义转换实现题中物理条件的化归,如图3所示,把题中阐述的内容情境转化为物理图景的表象,转化为学生所熟知的基本运动情境.

图3 通过语义转换实现化归
3.2解题过程中的化归思想运用
物理题中的条件与条件、条件与问题结论之间存在着差异性矛盾,解题过程就是利用化归思想有目的和有效地转化并解决矛盾的过程.从该角度剖析学生“一听就懂、一做就错”的现象,即学生缺乏将新问题转化为熟知问题解决的化归意识.
以下仅举几例从部分视角阐释化归思想在解题过程中的运用.
3.2.1构建物理模型转化——化复杂为简单
【例1】探究某种笔的弹跳问题时,把笔分成轻质弹簧、内芯和外壳3部分,其中内芯和外壳质量分别为m和4m.笔的弹跳过程分为3个阶段:
(1)把笔竖直倒立于水平硬桌面,下压外壳使其下端接触桌面如图4(a);
(2)由静止释放,外壳竖直上升至下端距桌面h1时,与静止的内芯碰撞如图4(b);
(3)碰后,内芯与外壳以共同的速度一起上升到外壳下端距桌面最大高度h2处,如图4(c).设内芯与外壳间的撞击力远大于笔所受重力,不计摩擦与空气阻力,重力加速度为g.

图4
化归思想运用分析:该题是重庆理综的高考题,涉及的是命题者捕捉到学生课间无意识玩的小游戏的绝佳命题素材,不少学生虽耳熟能详,但对于此类原始物理问题的物理建模转化有相当困难,难以下手.运用化归思想,通过等效简化和抽象,把问题中复杂的具体现象转换为简洁的物理模型,转化建模过程如下.
(1)转化构件模型:舍弃对各阶段过程没有实质性影响的外壳A和内芯B的形状、长度,把图5(a)里的长管状外壳A和柱状内芯B逐步转化为图5(b)(过渡形式)和(c),图5(d)是学生熟悉的常见块状形式(即构件模型);
(2)转化构件位置关系模型:舍弃对各阶段过程没有实质性影响的外壳A和内芯B的内外位置关系,转化为图5(d)所示的外壳A和内芯B的上下关系;

图5
(3)转化为熟悉的物理过程模型:等效的移动某些力的作用点(外壳A所受的外力作用点移动),忽略次要的影响因素(相对次要的重力、摩擦与空气阻力),使外壳与内芯碰撞“粘合”过程转化为学生熟悉的动量守恒过程.
3.2.2建立过程关系图像——化模糊为清晰
【例2】装甲车和战舰采用多层钢板比采用同样质量的单层钢板更能抵御穿甲弹的射击.通过对以下简化模型的计算可以粗略说明其原因.质量为2m,厚度为2d的钢板静止在水平光滑桌面上.质量为m的子弹以某一速度垂直射向该钢板,刚好能将钢板射穿.现把钢板分成厚度均为d,质量均为m的相同两块,间隔一段距离水平放置,如图6所示.若子弹以相同的速度垂直射向第一块钢板,穿出后再射向第二块钢板,求子弹射入第二块钢板的深度.设子弹在钢板中受到的阻力为恒力,且两块钢板不会发生碰撞,不计重力影响.
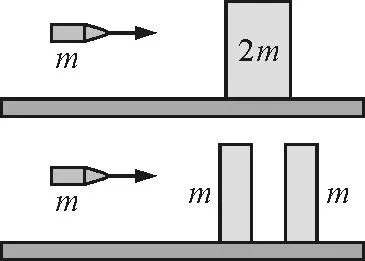
图6
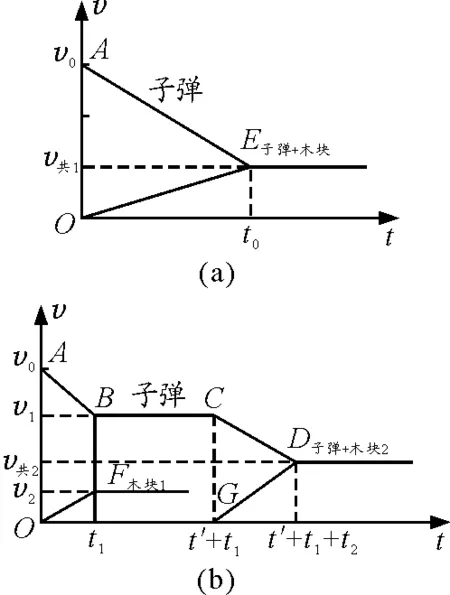
图7
化归思想运用分析:该题是全国理综高考题,题设物理情境是典型的“双重”子弹打木块模型,原标准答案(详细解答略)是运用动量守恒定律和功能原理求解,但是计算量大且过程复杂,运用化归思想将物理过程转化建立过程v-t图像,如图7(a)和(b),使得物理过程清晰显化,并简化过程计算,譬如原解3次运用动量守恒定律和功能原理方程,在此只运用1次动量守恒定律方程,且不必计算出v2和v共2,只需运用图像中的相关面积计算即可.
3.2.3情境图示降维处理——化抽象为直观
【例3】如图8所示,光滑斜面长为a,宽为b,倾角为θ,一物体从斜面左上方P点水平射入,而从斜面右下方顶点Q离开斜面,求入射初速度.

图8
化归思想运用分析:该题物理情境描述的是物体在三维立体斜面上的运动,不少学生缺乏空间想象能力,感觉较为抽象,分析不出物体在斜面上做“类平抛运动”.运用化归思想对情境示意图进行降维处理,将其转化为较为直观的二维平面侧视图9(a)和垂直斜面视线的俯视图9(b),则可将物体运动分解为在光滑斜面上沿b方向的速度为v的匀速直线运动和沿a方向的初速度为零加速度为a=gsinθ的匀加速直线运动,为学生解决问题铺平了道路.
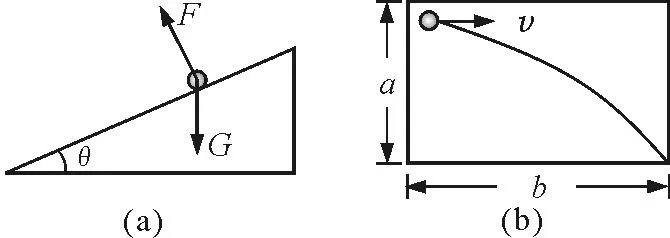
图9
3.2.4合理拆分物理过程——化整体为局部
【例4】如图10所示,沿水平方向放置一条平直光滑槽,它垂直穿过开有小孔的两平行薄板,板相距3.5L.槽内有两个质量均为m的小球A和B,球A带电荷量为+2q,球B带电荷量为-3q,两球由长为2L的轻杆相连,组成一带电系统.最初A和B分别静止于左板的两侧,离板的距离均为L.若视小球为质点,不计轻杆的质量,在两板间加上与槽平行向右的匀强电场E后(设槽和轻杆由特殊绝缘材料制成,不影响电场的分布),求:
(1)球B刚进入电场时,带电系统的速度大小;
(2)带电系统从开始运动到速度第一次为零所需的时间及球A相对右板的位置.
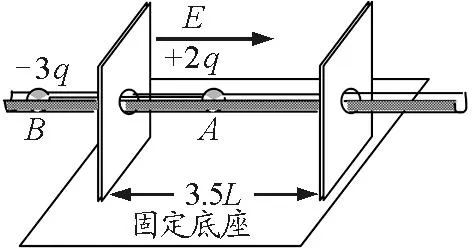
图10
化归思想运用分析:该题是典型的多过程问题,运用化归思想,利用“拆”字诀,用“慢镜头”方式将物理过程转化为几个子过程进行分析.如图11所示,图11(a)位置系统刚要运动,B在电场外,A在电场内,图11(b)位置B刚进入电场,A与B均在电场内,图11(c)位置A球刚要离开电场,A与B均在电场内,图11(d)位置B在电场内,A在电场外,系统末速度为零.由过程分析可得,(a)→(b)过程做匀加速直线运动,(b)→(c)过程做匀减速直线运动,(c)→(d)过程做匀减速直线运动.

图11
3.2.5巧妙运用合成分解——化陌生为熟悉

图12
(1)带电粒子第一次穿越x轴时横坐标x0;
(2)带电粒子在区域Ⅱ中到达最低点的纵坐标y0.
化归思想运用分析:该题第(2)问如图13(a)所示,根据A点位置的电场力、洛伦兹力和速度三者情况,可判断出该粒子所做运动是一种学生陌生的未知复杂曲线运动.运用化归思想转化未知复杂曲线运动,沿x和y轴方向分别分解洛伦兹力和速度,如图13(b)所示,可知fy=qE二力平衡,由此作为切入口,将未知复杂运动转化为沿x轴正方向的vx匀速直线运动和以速率为vy,qvyB为向心力的匀速圆周运动,而这两种运动恰是学生最为熟知的基本运动,问题便迎刃而解.
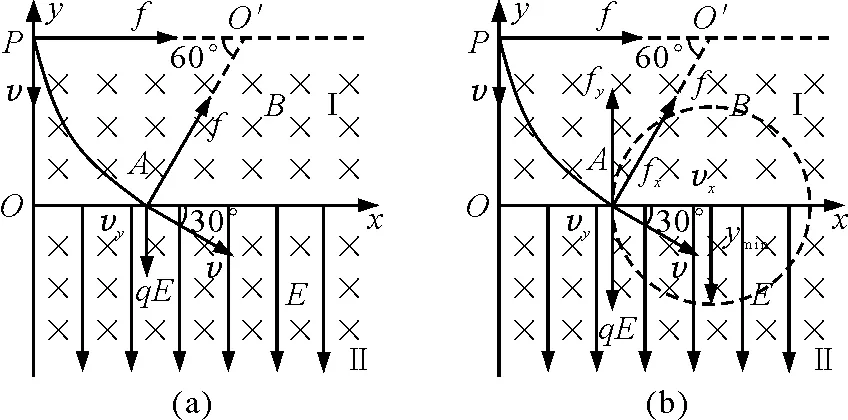
图13
3.2.6灵活转化参考系——化繁琐为方便
【例6】汽车甲以速度v1向前行驶,司机突然发现前方距甲d处有汽车乙正以较小速度v2同向匀速行驶,于是他立即刹车,使汽车做匀减速运动,为了使两车不相撞,加速度a应满足什么条件?
化归思想运用分析:该题传统求解以地面为参考系,甲乙两车满足不相撞的临界条件:
位移

速度
v1-at=v2
联立求解出时间t,然后再求出加速度a.运用化归思想,将参考系转化为乙车,则甲相对乙的运动转化为初速度为(v1-v2)、加速度为a的匀减速运动,不相撞的临界条件:甲车减速到与乙车车速相同时,甲相对乙的位移为d,即
0-(v1-v2)2=-2ad
化归思想的运用远非限于此,在此仅是对化归思想在物理解题过程中运用研究的抛砖引玉,期待引起专家同仁的共同探讨.
收稿日期:(2015-04-03)
