δ冲击条件下相关性竞争失效过程的系统可靠性建模
2016-01-12常春波,曾建潮
第一作者常春波男,博士生,1979年生
通信作者曾建潮男,博士生导师,1963年生
δ冲击条件下相关性竞争失效过程的系统可靠性建模
常春波1,2,曾建潮2
(1.兰州理工大学电信学院,兰州730050;2. 太原科技大学工业与系统工程研究所,太原030024)
摘要:研究系统受到δ冲击时,考虑系统自然退化和冲击两个竞争性失效过程间具有相关性时,系统可靠性的建模问题。相关性一方面表现为冲击造成系统退化量的增加,另一方面表现为系统的自然退化程度对冲击结果的影响。假设系统因冲击而失效的过程是δ冲击过程,通过系统自然退化过程和冲击过程的分布函数,导出了系统的可靠度函数,建立了系统可靠度模型的一般形式,并给出一种特例的具体形式,最后利用文献中的具体参数进行仿真,以验证模型的正确性和有效性。
关键词:竞争性失效;δ冲击;可靠性;相关性
基金项目:国家自然科学
收稿日期:2013-10-21修改稿收到日期:2014-05-10
中图分类号:TB114.3文献标志码:A
Reliability modeling for dependent competing failure processes under δ-shock
CHANGChun-bo1,2,ZENGJian-chao2(1. College of Electrical and Information Engineering, Lanzhou University of Technology, Lanzhou 730050, China;2. Division of Industrial and System Engineering, Taiyuan University of Science and Technology, Taiyuan030024, China)
Abstract:The system reliability modeling was studied considering the correlation between two s-dependent competing failure processes including degradation and shock when a system was subjected to δ-shock. On the one hand, shock process caused the additional abrupt degradation of the system; on the other hand, the degradation of the system affected the results of the shock process. Assuming that the system was subjected to δ-shock process, based on the distribution functions of the system natural degradation process and the shock process, the system’s reliability function was derived. The general form of the system’s reliability model was established and one of its specific forms was given. Finally, the simulation was preformed using parameters listed in a literature. The simulation results showed the correctness and validity of the model.
Key words:competing failure processes;δ-shock; reliability; dependent
系统在运行过程中,性能随时间的推移不断发生着退化,经过一段时间的运行后,最终失效。在这一过程中,其功能也可能会在某一时刻由于外部冲击突然丧失。即系统既会出现退化型失效(软失效),也可能会出现突发型失效(硬失效),系统的失效则是这两种失效模式竞争的结果[1]。
在有关系统可靠性建模的文献中,最初仅考虑自然退化或冲击单独造成系统的失效。而对于高可靠性、长寿命的系统,基于退化过程的分布函数则能更有效的反映系统失效的机理过程,并且能提供一种间接的可靠性预测方法。因此,自20世纪90年代早期,大量的文献用退化过程建模来分析系统的可靠性和统计特性[2-4]。对于那些易受到冲击影响的系统,已有文献对冲击的建模也进行了广泛的研究,并归纳为四种类型[5-8]:①极端冲击模型。系统的失效是由于某个量级超过设定阈值的冲击造成的;②累计冲击模型。系统的失效是由于冲击造成的退化量累计到一定程度造成的;③连续冲击(run shock model)模型。系统的失效是由于k个连续的量级达到一定程度的冲击造成的;④δ冲击模型。系统的失效是由于两个连续冲击的间隔时间小于某一阈值δ而造成的。
在由多个退化过程组成的竞争性失效过程的可靠性分析方面。Ye等[9]考虑了自然退化和极端冲击共同作用时系统的可靠度模型。Wang等[10]考虑了一种包含两种冲击的双冲击过程。Li等[11-12]分析了由两种退化过程和一种冲击过程构成的3个独立的失效过程,考虑了3个失效过程间的竞争性,只要有任意一个过程达到失效阈值,就认为系统失效。在这些模型中,只考虑了多个退化过程间的竞争性,但均假设各个过程间是独立的,互相不影响。
在考虑自然退化与冲击过程有相互影响方面,Wang等[13]分别考虑了冲击对自然退化的两种影响方式,分别是冲击导致系统失效率的增大和退化量的增加,在假设系统受到极端冲击的条件下,给出了自然退化过程的可靠性模型。Peng等[14]认为系统的自然退化和累计冲击是相关的,累计冲击造成了的系统退化量的增加,在该假设条件下推导出了系统的可靠度函数。Jiang等[15-16]同样考虑了冲击导致退化量的增加,并在此基础上提出了冲击失效的阈值可变性,但阈值的变化不是与系统的退化程度有关,而是因冲击自身满足某种条件引起的阈值变化。
在现有的文献中,大多数只考虑冲击对自然退化的影响。关于自然退化对冲击的影响,现有文献并没有过多考虑。然而,在实际的系统运行过程中,系统的自然退化程度对冲击的结果也会有一定的影响。例如,新投入使用的电力设备,可靠度往往很高,当电网发生波动或受到雷击时,在一定的范围内(强度或频率),一般不会造成损坏。但经过长时间的运行后,相同强度或频率的冲击,就可能造成设备的失效,设备只能承受强度较小或频率较低的冲击,即系统因冲击而失效的阈值随着系统的退化而降低。
在冲击模型的四种类型中,极端冲击、累计冲击和连续冲击模型均考虑的是冲击的量级对系统可靠性的影响,而δ冲击则考虑的是冲击的间隔时间或频率对系统的影响。Li等[17-18]研究了δ冲击条件下复杂系统的可靠性和寿命特性。Ery1lmaz[19]利用连续冲击的思想推广δ冲击模型,推导了系统的生存函数和平均故障时间,并给出了同时考虑连续冲击的量级和间隔时间下系统的生存函数。Yeh[20]考虑δ冲击的失效阈值δ是可变的,随着系统维修次数的增加,δ变大或变小。在实际的系统运行过程中,系统受到δ冲击的情况也很常见,如雨季时多次密集降雨导致的泥石流、山体滑坡,多个洪峰对水库大坝的影响,电网的频繁波动对电力设备造成的损害等。
本文假设系统因冲击而失效的过程是δ冲击过程,自然退化和冲击过程的相关性一方面表现为冲击造成系统退化量的增加,另一方面表现为自然退化过程对系统因冲击而失效的阈值的影响。文中通过系统自然退化过程和冲击过程的分布函数,推导出了系统的可靠度函数,建立了系统可靠度模型的一般形式和一种特例的具体形式,最后利用文献中的具体参数进行了数值仿真。
1系统可靠性问题的描述
假设系统在服役期内,受到包括自然退化和冲击两个退化过程的影响。系统受到的冲击过程为δ冲击,即两次冲击的间隔时间小于某一阈值时,系统失效。系统的运行过程根据退化程度划分为运行前期和运行后期两个区间,在每个区间内,系统因冲击而失效的阈值不同,以反映系统的实际运行情况。冲击对系统的另一个影响是每次冲击都会造成系统退化量的增加。
系统总的退化量包括自然退化的退化量和每次受到冲击时造成的退化量,随着服役时间的增加,其退化量不断增大,当退化量超过某一阈值时,认为系统不再适合服役,这一阈值称为系统的失效阈值,达到失效阈值的系统认为是已经失效的系统。
这样,系统的失效就有两种情况:系统总的退化量达到失效阈值或受到的冲击的间隔时间小于某一阈值。其中任何一个条件符合,系统均会失效。系统的失效则可以看作是两种失效模式竞争的结果。

图1 δ冲击下系统退化过程的示意图 Fig.1 Schemes of system degradation process subject to δ-shock
系统有两种失效模式,即,系统的退化量达到某一阈值H或冲击的间隔时间小于阈值δ或bδ,其中任何一个条件符合,系统均会失效。
系统的退化量由两部分构成,包括系统自然退化的退化量和冲击造成的退化量,当总的退化量达到H时,系统失效(软失效)。
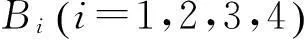
2对自然退化过程和冲击过程的一些具体假设
2.1 系统自然退化过程的假设
系统的自然退化过程假设为一随机过程,可以为任意一种退化类型,包括线性和非线性退化过程,这里假设系统的退化量X(t)在某时刻t的分布函数为G(x,t)。
2.2 冲击过程的假设
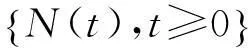
若t时刻冲击到达的个数为N(t),则在t时刻由冲击造成的退化量的总量为:
(1)

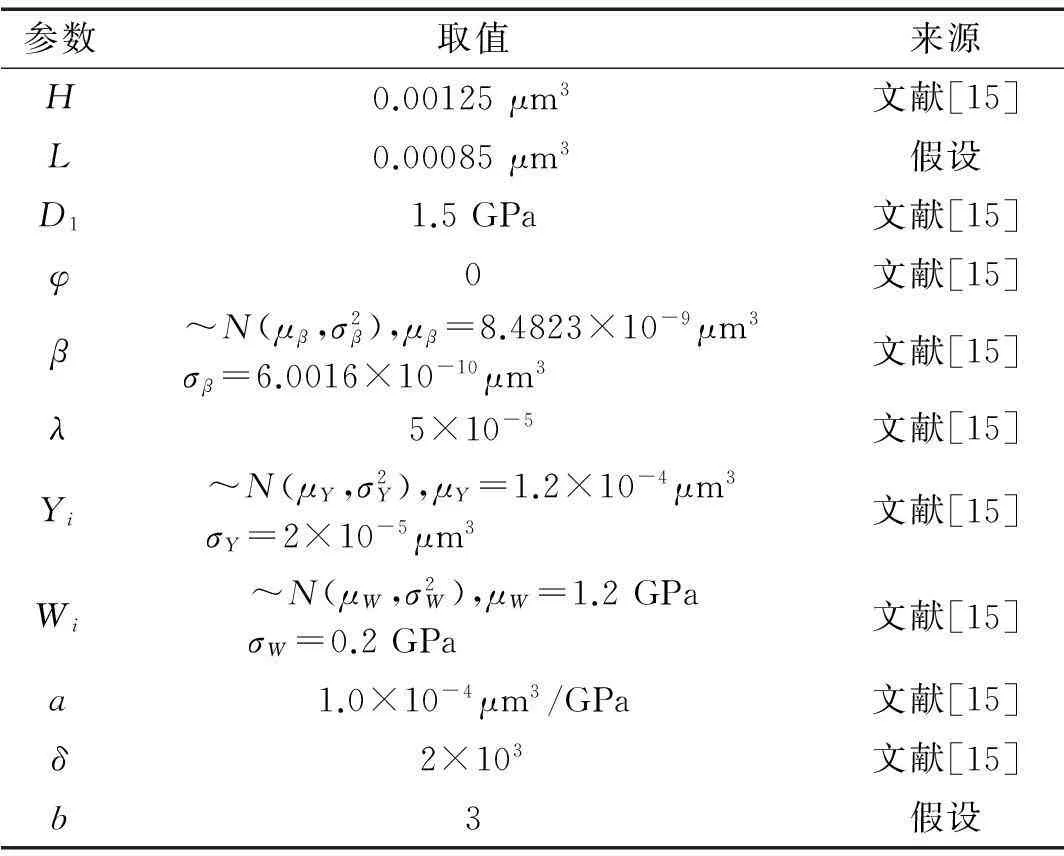
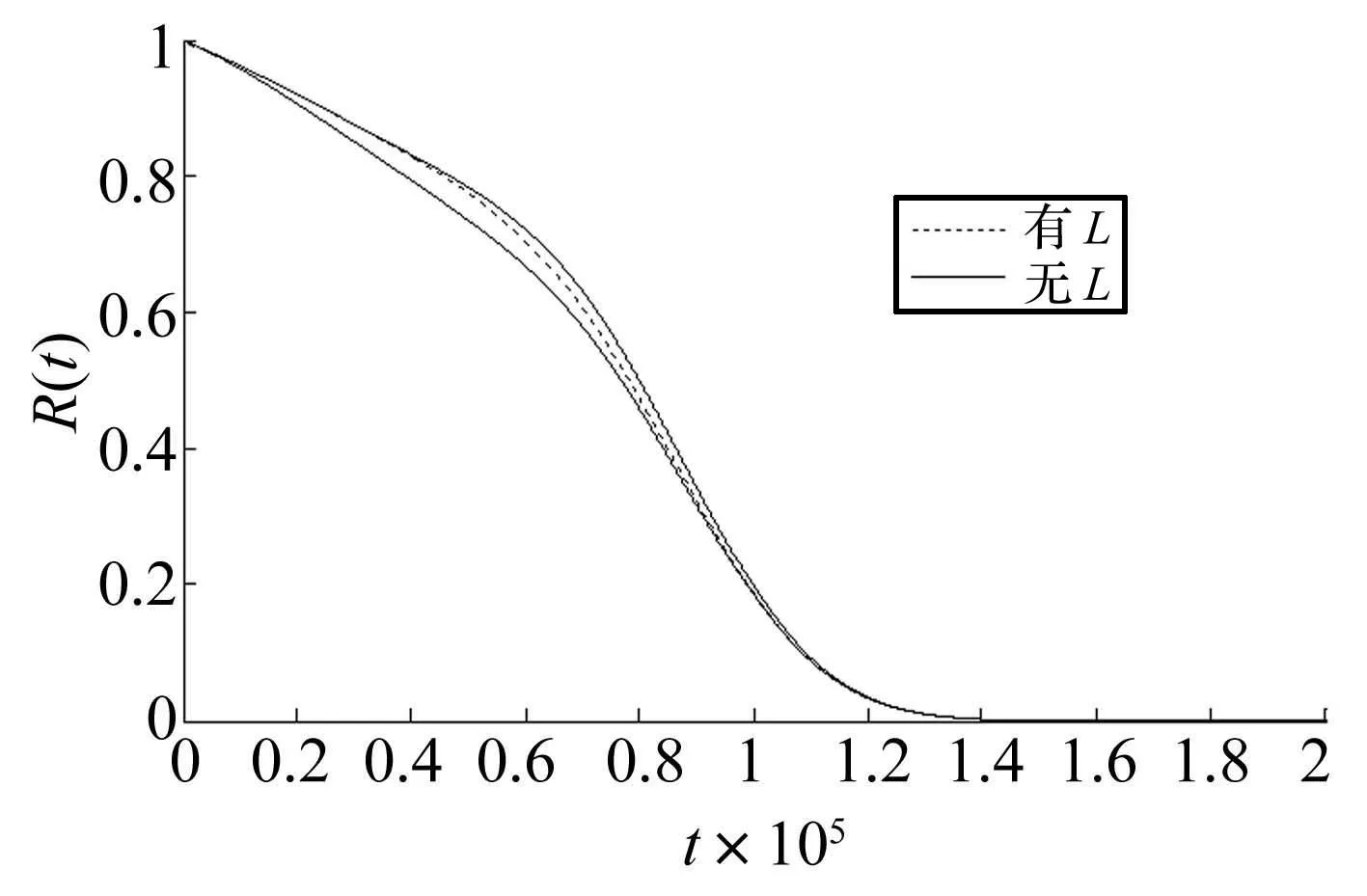
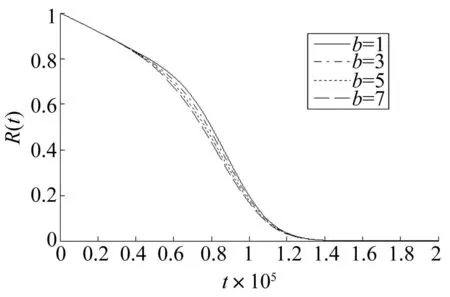
FX(x,t)=P(Xs(t) G( x, t)exp(- λt)+ (2) 其中第一项为冲击的个数为0时,系统的退化量小于x的概率,第二项为冲击的个数为i,i=1,2…,∞时系统总的退化量小于x的概率。 若系统的失效阈值为H,则在时刻t系统不发生软失效的概率为 P(Xs(t) (3) 如图1所示,系统不发生硬失效的条件为所有冲击的幅值均小于阈值,间隔时间均大于阈值,设第i次冲击后系统不发生硬失效的概率为: P(Wi 式中i=1,2,…,∞,FW(w)为Wi的累积分布函数。 在冲击和自然退化竞争失效的条件下,系统在t时刻的可靠度为: (4) 3系统可靠度函数的建立 系统因冲击而失效的模式为:当退化量XS(t) 根据t时刻系统受到冲击的个数,系统的可靠度函数可以分以下几种情况讨论: (1)t时刻冲击的个数为0,此时主要考虑系统不发生软失效的概率: R(t|N(t)=0)=P(XS(t) P(X(t) (5) (2)t时刻冲击的个数为1。由于只有一次冲击,不存在时间间隔的问题,所以只考虑冲击的幅值和系统总退化量小于阈值的概率: R(t|N(t)=1)=P(W1 XS(t) P(W1 (6) (3)t时刻冲击的个数大于1。由于系统在运行的前期和后期,发生硬失效的阈值不同,因此,根据系统的退化量又可分为两种情况: 1)t时刻系统的退化量XS(t) R(t|N(t)=i,2≤i≤[t/δ]+1)= (7) 2)t时刻系统的退化量L≤XS(t) R(t|N(t)=i≥2)= XS(tj)≥L,L≤XS(t) (8) 若已知t时刻系统受到i个冲击,且系统的退化量在L和H之间,这时系统不失效的概率应包括:所有的冲击的幅值都小于D1的概率,第j-1个冲击时系统的退化量小于L的概率,第j个冲击时系统的退化量大于L的概率,前j-1个冲击的间隔时间大于δ的概率,剩余冲击的间隔时间大于bδ的概率,系统总的退化量在L和H之间的概率。 其中I(A)为指示函数,当A成立时,I(A)=1,反之I(A)=0。 综合以上三种情况,系统的可靠度函数为: R(t)=P(X(t) (9) 将式(2)代入,可得系统可靠度函数的一般形式为: (10) 式(10)为冲击的到达服从速率为λ的泊松过程{N(t),t≥0}时,系统可靠度函数的一般形式。 在该式中,系统的退化量X(t)在某时刻t的分布函数以符号G(x,t)表示,系统的退化可以为线性退化过程,也可以为非线性退化过程,G(x,t)的具体形式则取决于系统的实际退化过程。 根据系统的实际情况,不同的退化过程采用不同的具体形式。 式(10)中tj-1为第j-1个冲击到达的时刻,tj为第j个冲击到达的时刻,均为随机变量,考虑用各自的均值代替。 设{N(t),t≥0}是参数为λ的泊松过程,如果已知在[0,t)内有i个冲击到达,则i个冲击的到达时刻τ1<τ2<…τi和i个相互独立同服从[0,t)上均匀分布的随机变量U1,U2,…Ui的次序统计量U(1) 对于次序统计量的密度函数,有如下结论[22]: 设总体X的密度函数为p(x),分布函数为F(x),x1,x2,…,xn为样本,则第k个次序统计量x(k)的密度函数为: pk(x)= (11) 若总体X服从[0,t)内的均匀分布,则第k个次序统计量x(k)的密度函数为: (12) 根据期望值(均值)的定义求x(k)的期望: 4实例分析 第3节中得到的可靠度函数为冲击的到达服从速 (13) 为了分析可靠度函数的正确性,采用文献[15]中的参数进行仿真。文献[15]的参数选自美国圣地亚国家实验室微机电系统可靠性试验时记录的参数值,具有典型的竞争性失效过程。 表1 可靠度分析的参数值 仿真的参数如表1所示。表中假设的参数可以根据系统的实际情况进行设定,仿真过程中分析了这些参数改变时对系统可靠性的影响。 将表1中的参数代入式(13),得到的系统可靠度曲线如图2所示。图中曲线“有L”为采用本文可靠度模型得到的曲线,曲线“无L”为文献[15]中可靠度模型的曲线。可以看到,在加入系统中后期的控制线L后,系统的可靠度有所降低,反映了对于相同间隔时间的冲击,系统运行的前期和后期会有不同的冲击结果这一现象。 图2 系统的可靠度曲线 Fig.2 System reliability curve 图3为冲击失效阈值的系数b分别为1、3、5、7时系统的可靠度曲线,可以看到,随着b的增加,系统的可靠度随之降低。b增大,意味着系统进入后期时,要求冲击的间隔时间更长,因此,在冲击的到达速率保持不变的前提下,系统更容易失效,即系统的可靠度会降低。 图3 失效阈值系数b变化时 系统的可靠度曲线的变化趋势 Fig.3 Trend of reliability curve with b changes 图4为系统中后期的控制线L分别为0.001 05、0.000 85、0.000 65和0.000 45时系统的可靠度曲线,可以看到,随着控制线L的降低,系统的可靠度也随之降低,且可靠度降低的时间点提前了,对应实际运行时系统更早的进入中后期。L对可靠度曲线的影响主要集中在系统运行的中后期。 图4 控制线L变化时系统的可靠度曲线的变化趋势 Fig.4 Trend of reliability curve with L changes 图5 δ变化时系统的可靠度曲线的变化趋势 Fig.5 Trend of reliability curve with δ changes 图5为δ变化时,对可靠度曲线的影响。δ的取值分别为1 000、1 500、2 000和2 500时,系统的可靠度曲线。由于系统的设定是两个连续冲击的间隔时间小于δ时,系统失效,所以当冲击的速率不变,δ变大时,冲击的间隔时间更容易小于δ,即系统更容易失效,表现为系统的可靠度降低。 5结论 本文根据系统退化量的不同,将系统的运行过程分为运行前期和运行后期两个区间。在不同的区间,对δ冲击设定不同的失效阈值,即对于相同间隔时间的冲击,系统运行的前期和后期会有不同的冲击结果。利用系统和冲击的分布函数,建立系统可靠度模型的一般形式,并给出了一个具体的形式,通过仿真验证,可靠度模型达到了本文设定的目的。 本文的后续工作是将冲击的失效阈值设定为系统退化量的函数研究其可靠性,这样能更准确、及时的反映冲击的失效阈值随系统退化量变化的现象。 参考文献 [1]赵建印, 基于性能退化数据的可靠性建模与应用研究[D]. 长沙:国防科学技术大学, 2005. [2]Lu C J, Meeker W O. Using degradation measures to estimate a time-to-failure distribution[J]. Technometrics, 1993, 35(2): 161-174. [3]Singpurwalla N D. Survival in dynamic environments[J]. Statistical Science, 1995, 10(1): 86-103. [4]Kharoufeh J P, Cox S M. Stochastic models for degradation-based reliability[J]. IIE Transactions, 2005, 37(6): 533-542. [5]Nakagawa T. Shock and damage models in reliability theory[M]. Springer, 2007. [6]Liu Y, Huang H Z, Pham H. Reliability evaluation of systems with degradation and random shocks[C]. Reliability and Maintainability Symposium, RAMS Annual. IEEE, 2008: 328-333. [7]Chien Y H, Sheu S H, Zhang Z G, et al. An extended optimal replacement model of systems subject to shocks [J]. European Journal of Operational Research, 2006, 175(1): 399-412. [8]Bai J M, Li Z H, Kong X B. Generalized shock models based on a cluster point process[J]. IEEE Transactions on Reliability, 2006, 55(3): 542-550. [9]Ye Z S, Tang L C, Xu H Y. A distribution-based systems reliability model under extreme shocks and natural degradation [J]. IEEE Transactions on Reliability, 2011, 60(1): 246-256. [10]Wang G J, Zhang Y L. A shock model with two-type failures and optimal replacement policy[J]. International Journal of Systems Science, 2005, 36(4): 209-214. [11]Li W, Pham H. An inspection-maintenance model for systems with multiple competing processes[J]. IEEE Transactions on Reliability, 2005, 54(2): 318-327. [12]Li W, Pham H. Reliability modeling of multi-state degraded systems with multi-competing failures and random shocks[J]. IEEE Transactions on Reliability, 2005, 54(2): 297-303. [13]Wang Z, Huang H Z, Li Y, et al. An approach to reliability assessment under degradation and shock process[J]. IEEE Transactions on Reliability, 2011, 60(4): 852-863. [14]Peng H, Feng Q M,Coit D W.Reliability and maintenance modeling for systems subject to multiple dependent competing failure processes[J].IIE Transactions, 2011,43:12-22. [15]Jiang L, Feng Q, Coit D W. Reliability and maintenance modeling for dependent competing failure processes with shifting failure thresholds [J]. IEEE Transactions on Reliability, 2012, 61(4): 932-948. [16]苏春, 瞿众洲, 郝会兵. 考虑相关竞争故障过程及变动阈值的可靠性评估[J]. 东南大学学报(英文版), 2013, 29(1), 52-56. SU Chun, QU Zhong-zhou, HAO Hui-bing. Reliability assessment considering dependent competing failure process and shifting-threshold[J].Journal of Southeast University(English Edition), 2013, 29(1): 52-56. [17]Li Z H, Kong X B.Life behavior of δ-shock model[J]. Statist. Probab. Lett,2007,77:577-587. [18]Li Z H, Zhao P. Reliability analysis on the δ-shock model of complex systems[J]. IEEE Trans. Reliab,2007, 56:340-348. [19]Ery1lmaz S. Generalized δ-shock model via runs[J]. Statistics & Probability Letters, 2012, 82(2): 326-331. [20]Lam Y, Zhang Y L. A geometric-process maintenance model for a deteriorating system under a random environment[J]. Reliability, IEEE Transactions on, 2003, 52(1): 83-89. [21]张卓奎, 陈慧婵. 随机过程[M]. 西安: 西安电子科技大学出版社, 2003. [22]吴赣昌, 概率论与数理统计(理工类·第四版)[M]. 北京: 中国人民大学出版社, 2011.
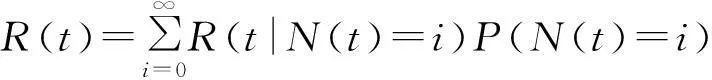
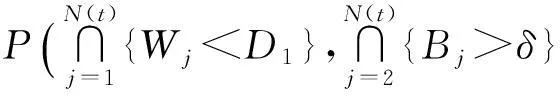
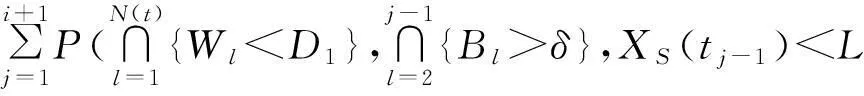

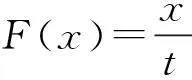
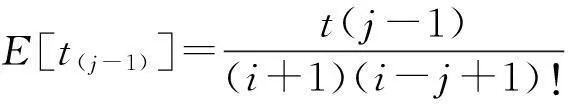
4.1 可靠度函数形式的具体化

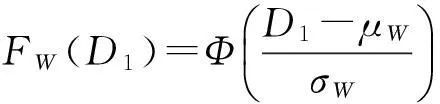
4.2 参数的选取