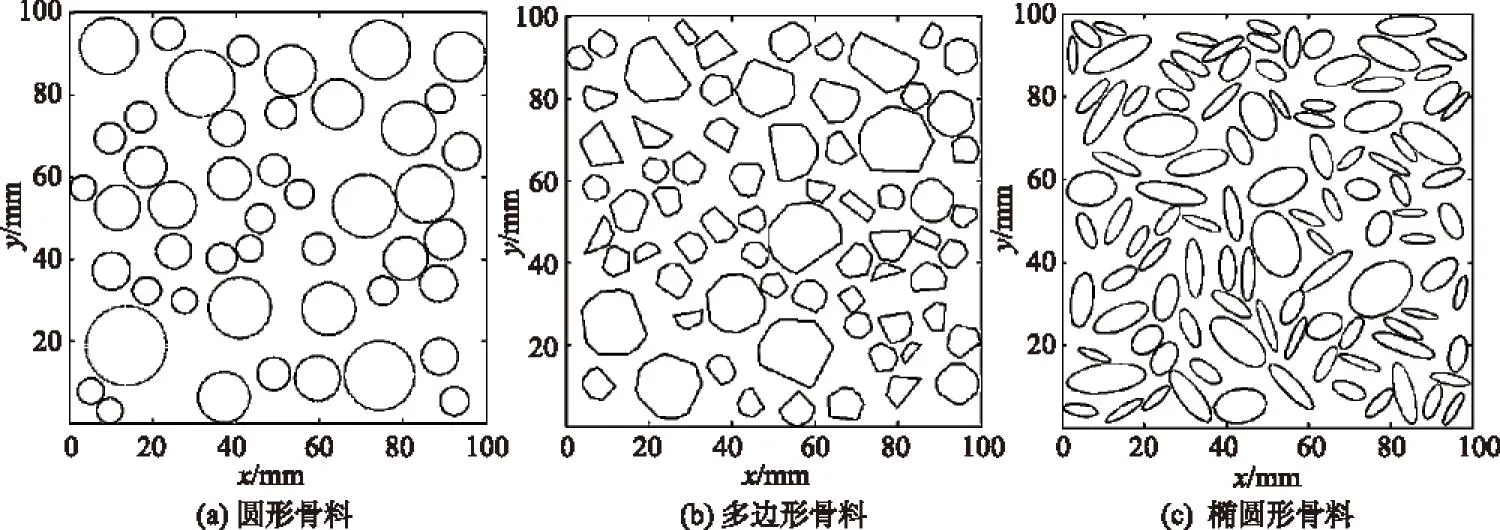
基于细观层次的混凝土随机骨料建模
2016-01-11屈瑾,娄宗科,刘兆松
基于细观层次的混凝土随机骨料建模
屈瑾, 娄宗科,刘兆松
(西北农林科技大学 水利与建筑工程学院,陕西 杨凌712100)
摘要:在细观层次上,将混凝土视为由骨料、砂浆和二者之间的界面层构成的三相复合材料,而界面层是混凝土的最薄弱环节,也是混凝土抗拉强度低的主要原因。基于MATLAB软件生成圆形、多边形和椭圆形3种随机骨料模型,并生成一定厚度的骨料界面层,结合有限元软件ABAQUS划分界面层单元,建立二维混凝土细观数值模型。通过算例表明:骨料投放算法简单,模型真实可靠。通过引入界面层并对其进行网格剖分,对多边形骨料模型进行单轴拉伸试验,得到的应力-应变曲线基本符合宏观混凝土单轴拉伸试验结果,为后续研究混凝土的损伤断裂机理提供了数值模拟基础,并且有效地解决了MATLAB,AUTOCAD和有限元软件之间的接口问题。数字模拟生成的多边形骨料分布情况占有率与真实骨料最接近,可用作混凝土的损伤断裂机理分析。
关键词:混凝土;随机骨料;抗拉强度;数值模拟;MATLAB
中图分类号:TU471.91文献标志码:A
收稿日期:2014-04-28;修回日期:2014-05-11
基金项目:国家科技支撑计划课题(2012BAB03B01);江苏省基础研究计划(自然科学基金)资助项目(BK2012414)
作者简介:王鑫浩(1990-),男,安徽滁州人,硕士研究生,主要从事海洋地理信息技术应用和区域规划研究,(电话)025-83787579(电子信箱)xinghaobsb@hotmail.com。
DOI:10.3969/j.issn.1001-5485.2015.04.026
1研究背景
随着科学技术的不断发展,对于混凝土的研究不仅仅局限于宏观和微观层次,其细观力学性能也越来越多地被人们所认识。在细观层次上,认为混凝土是由骨料、砂浆和二者之间的黏结界面构成的一种非均质的多相复合材料。对混凝土进行数值模拟,了解混凝土中骨料和砂浆及两者之间界面层的破坏过程及其细观力学性能。混凝土的细观力学研究不仅能正确反映出混凝土复合材料性能,而且能与实际的宏观力学性能相联系。
在混凝土中,混凝土的性能与骨料的形状、配合比等有很大的关系,因此,对混凝土骨料形状的生成就成了混凝土数值模拟的一个重要前提。早在1984年就开始研究混凝土骨料的数值模拟问题,20世纪90年代初,Bazant等[1-2]提出随机颗粒模型,采用随机分布的颗粒来模拟混凝土骨料,生成的圆形和球形骨料模型接近卵石骨料的形态,但与工程实际中的碎石骨料差异较大。王宗敏等[3]提出二维混凝土任意形状骨料随机投放算法,借助Monte Carlo抽样原理,采用极坐标方式生成随机多边形。高政国等[4]提出以面积为参数的骨料侵入判别准则,按多边形随机生长方式建立随机骨料的投放算法,采用凸型骨料假定的算法简单,但所建立的模型骨料含量较低, 且没有考虑实际骨料级配。宋来忠等[5]针对矩形区域产生大量随机分布椭圆的算法进行了改进,但仍不能满足实际工程中的需要。唐欣薇等[6]基于混凝土随机骨料生长方式,提出了骨料投放的“分层摆放法”,极大地提高了骨料的投放效率,但没有考虑骨料与砂浆之间的界面层。目前随机骨料的建模大都将重心放在算法的研究和骨料的干涉判断上[7],对于界面层的讨论较少。且本文利用MATLAB软件自编圆形、多边形和椭圆形3种二维剖面形状骨料的生成程序,详细写出各自的投放过程,在此基础上引入界面层使骨料更具真实性,并结合有限元软件对混凝土的三相单元进行网格剖分,生成网格模型,为研究混凝土的损伤破坏机理奠定基础。
2随机骨料模型的生成
在骨料生成过程中应该满足如下条件:
(1) 确定骨料的投放区域。
(2) 确定骨料的粒径、级配及骨料所占的百分比。
(3) 骨料参数由随机数控制,使得其在一定范围内呈均匀分布。
(4) 保证相邻骨料之间不能相互干涉。
2.1 骨料的级配
骨料级配包含2方面的内容[8]:一方面是粒径问题,即颗粒的尺寸大小问题;另一方面是粒径分布的问题,即各粒径数量相对多少。目前的混凝土级配理论主要有2种:连续级配和间断级配。连续级配即颗粒由小到大,每级粗骨料都占有一定比例,相邻2级粒径之比为2。间断级配即认为剔除某些中间粒径颗粒,用小颗粒的粒径直接和大颗粒的粒径相配,颗粒级差大,空隙率的降低比连续级配快得多,可最大限度地发挥骨料的骨架作用,减少水泥用量。
美国科学家富勒(W.B.Fuller)于20世纪初提出了理想的最大密实度级配曲线,即富勒曲线。其做法是首先将砂石分级后进行级配,找出相邻2级的最优比例,然后整理成抛物线形式。其抛物线为
(1)
式中:P为通过筛孔D骨料的质量百分比;Dmax为最大粒径。
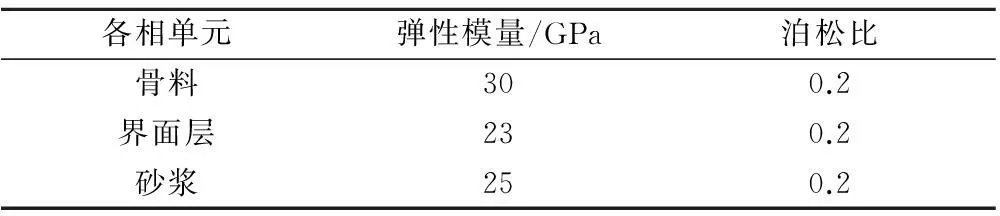
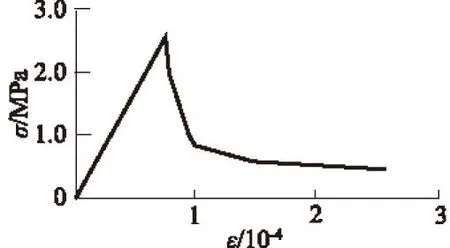
瓦拉文(Walraven)等人将富勒(Fuller)三维骨料级配曲线转化为二维平面内任意直径骨料出现的概率。Walraven的研究工作表明:基于富勒公式,将三维级配曲线转化为试件内截面上任一点具有骨料直径D (2) 式中:D0为筛孔直径;Pk为骨料体积占总体积的百分比。 圆形骨料的生成算法比较简单,控制参数有圆心坐标x,y和半径R,模型的生成投放过程如下: (1) 生成骨料的投放区域。 (2) 确定骨料所占的面积百分比,用于判断是否停止生成骨料,如满足则停止生成,反之进行下一步。 (3) 确定满足随机分布的骨料控制参数,即圆心坐标x,y和半径R。 (4) 判断骨料是否满足边界条件。其中,x,y分别为[R,A-R]和[R,B-R]上均匀分布的随机变量,A为投放区域宽度,B为投放区域高度,若满足则执行下一步,反之返回(3)。 (5) 判断新生成的骨料是否与已生成的骨料发生干涉,依据是 (3) 式中η为骨料范围影响系数,取1.05。若发生干涉,则返回(3);反之,输出参数R,x,y。 (6) 将输出的随机参数连接起来生成圆形骨料。 人工骨料多是凸多面体,因此在二维多边形骨料生成中常保证骨料为凸性。在以往的方法[3]中,首先生成随机三角形基骨料,然后向外延伸生成任意凸多边形骨料,此方法的不足是需要进行骨料的凸性判断[10],生成效率不是很高。本文在研究中为保证骨料为凸性,引入了一种简洁有效的新方法,以随机生成的圆形骨料为基础生成凸多边骨料模型,即在圆周上随机生成多边形的顶点数N,然后顺次连接起来生成多边形,多边形的顶点是由随机生成的N个相对于x轴的角度αi确定的。这种算法既可以生成等边数的多边形,也可以生成不等边数的多边形,并且可以保证生成的多边形均为凸多边形,省去了凸性判断的步骤。对于干涉的判断只需要判断圆形骨料是否干涉即可。模型的生成投放过程如下: (1) 生成骨料的投放区域。 (2) 确定骨料所占的面积百分比,用于判断是否停止生成骨料,如满足则停止生成,反之进行下一步。 (3) 确定满足随机分布的骨料控制参数,即圆心坐标x,y和半径R,凸多边形的顶点个数N及顶点对应的角度α; (4) 随机生成N个角度,确定多边形的N个顶点坐标,并顺次连接各顶点,生成多边形骨料。 以往对椭圆形骨料干涉判断有很多种,可以利用两椭圆的代数条件判断[7],但算法精度有待提高,也可以用一个椭圆外接多边形去逼近椭圆[11]。本文基于面积准则,根据多边形的面积与椭圆矩形的面积关系判断两骨料是否干涉。模型的生成投放过程如下: (1) 生成骨料的投放区域。 (2) 判断是否停止生成骨料,当骨料面积占截面面积的百分比大于设定的百分比时停止生成骨料,否则进行下一步。 (3) 确定满足随机分布的骨料控制参数,即形心坐标x和y,长轴a,长短轴的比率η以及长轴绕x轴正方向的旋转系数α。 (4) 判断骨料是否满足边界条件,若不满足则返回(3),否则进行下一步。 (5) 利用面积准则判断新生成的骨料是否与已生成的骨料发生干涉。 (6) 将输出的随机参数连接起来生成椭圆骨料。 3界面层的生成 混凝土材料的本质特征是不均匀性,由于泌水、干缩和温度变化等原因会使得骨料和水泥砂浆之间产生初始裂缝,而其发展直接影响混凝土的宏观力学性能。本文在编写投放过程的基础上,引入界面层,将3种形状的骨料边界坐标复制到AUTOCAD命令窗口中,生成骨料模型,然后设置一定厚度的界面层,并将剩余的部分作为砂浆模型,然后生成细观结构矢量图,输出扩展名为.dxf的图形文件,为导入有限元软件进行网格剖分做准备。 图1 3种二维骨料模型 Fig.1 Models of two-dimensional aggregates 图2 3种二维骨料的有限元网格模型 Fig.2 Finite element models of two-dimensional aggregates 4有限元网格模型的生成与加载 在细观层次上认为混凝土是由骨料、砂浆和二者之间的界面层组成的三相复合非均质材料,所以在模型的建立时要分别对骨料单元、界面单元和砂浆单元赋予不同的力学特性[12]。混凝土在承载后的破坏是由微裂缝的萌生和扩展引起的,所以本文用弹性损伤力学本构模型描述各相单元的力学特性。混凝土各相单元的材料特性参数见表1。 将生成的.dxf图形文件导入到有限元软件ABAQUS中进行网格划分,其中骨料采用三角形单元,界面和砂浆采用四边形占优单元,允许在界面层区域含有少量的三角形单元,最终生成骨料二维混凝土有限元网格数值模型。 对生成的混凝土数值模型进行裂缝扩展分析[9],首先破坏的是微裂缝所在的界面单元,随着加载过程的继续,微裂缝不断扩展直至贯通,最终试件丧失承载能力,验证了界面层是混凝土的最薄弱环节,界面单元的力学性能也决定了混凝土的宏观差异。 表1 混凝土各相单元的材料特性参数 Table 1 Material parameters of concrete’s each phase 5本文算例 下面分别给出圆形、多边形和椭圆形骨料的模型实例,说明本文生成骨料的有效性和ABAQUS网格剖分的实用性。 本文算例均采用边长为100 mm×100 mm的混凝土试件,骨料的投放率为40%,生成的随机骨料模型见图1(x,y为混凝土试件边长),用ABAQUS软件进行网格剖分的有限元网格模型见图2。其中,圆形骨料有限元网格模型含有骨料单元(CPS3)2 382个,砂浆单元(CPS4R)1 677个,界面单元(CPS3,CPS4R)304,405个;多边形骨料有限元网格模型含有骨料单元(CPS3)3 839个,砂浆单元(CPS4R)2 429个,界面单元(CPS3,CPS4R)690,2 169个;椭圆形骨料有限元网格模型含有骨料单元(CPS3)4 228个,砂浆单元(CPS4R)3 339个,界面单元(CPS3,CPS4R)558,16 307个。 图3 多边形骨料单轴 拉伸试验应力-应变曲线 Fig.3 Stress-strain curve of uniaxial tensile test on polygonal aggregate 用生成的混凝土随机骨料与同截面尺寸的真实二级配骨料(中石∶小石为45%∶55%)进行对比分析,可知在截面尺寸相等的条件下,数值模拟生成的多边形骨料的分布情况及面积占有率与真实骨料最接近,因此在一定程度上,可以用多边形骨料模拟真实混凝土的损伤断裂性能。 在ABAQUS软件中对多边形骨料模型进行单轴拉伸试验,采用位移加载方式进行控制,底边节点法向约束,加载位移步长0.001 mm/步,最终得到的应力-应变关系如图3所示。 6结语 本文通过对已有二维混凝土骨料生成算法的分析,利用MATLAB软件自编圆形、多边形和椭圆形3种二维剖面形状的模型生成程序,结合AUTOCAD及ABAQUS软件模拟了具有一定尺寸和骨料投放率的混凝土试件,结果表明生成的骨料投放算法简单,模型真实可靠,且其随机性也满足要求,并得到数值模拟生成的多边形骨料的分布情况及面积占有率与真实骨料最接近。通过引入界面层,对其进行有限单元剖分,为后续研究混凝土的损伤断裂机理提供了数值模拟基础,且有效地解决了MATLAB,AUTOCAD和有限元软件之间的接口问题。对多边形骨料模型进行单轴拉伸试验得到的应力-应变曲线,基本符合宏观混凝土单轴拉伸试验结果,为以后在细观层次上研究混凝土性能奠定了基础。本文的不足在于骨料的级配较简单,且其投放率还需要进一步提高。对于界面层对混凝土损伤断裂性能的影响仍需要进行更深入的研究,这也是作者目前的工作之一。 参考文献: [1]BAZANT Z P, TABBARA M R. Random Particle Models for Fracture of Aggregate or Fiber Composites[J]. Journal of Engineering Mechanics, ASCE, 1990, 116(8): 1686-1705. [2]BAZANT Z P. Crack Band Theory for Fracture of Concrete[J]. Material and Structures, 1983,16(3): 155-177. [3]王宗敏.不均质材料(混凝土)裂隙扩展及宏观计算强度与变形[D].北京:清华大学,1996. (WANG Zong-min. Crack Extension of Heterogeneous Materials (Concrete) and Macroscopic Strength and Deformation Calculation[D]. Beijing: Tsinghua University,1996. (in Chinese)) [4]高政国,刘光廷.二维混凝土随机骨料模型研究[J].清华大学学报(自然科学版),2003,43(5):710-714. (GAO Zheng-guo, LIU Guang-ting. Two-dimensional Random Aggregate Structure for Concrete[J]. Journal of Tsinghua University(Science and Technology),2003,43(5):710-714. (in Chinese)) [5]宋来忠.具有大量椭圆随机分布区域的数值模拟 及应用[J].计算力学学报,2012,29(5):662-667. (SONG Lai-zhong. Numerical Simulation Method for the Domain with Large Number of Random Ellipse Grains and Their Application[J]. Chinese Journal of Computational Mechanics, 2012, 29(5): 662-667. (in Chinese)) [6]唐欣薇.随机骨料的分层摆放法及有限元坐标的生成[J].清华大学学报:自然科学版,2008,48(12):2048-2052. (TANG Xin-wei. Layering Disposition and FE Coordinate Generation for Random Aggregate Arrangements[J]. Journal of Tsinghua University (Science and Technology), 2008,48(12):2048-2052. (in Chinese)) [7]高巧红,关振群,顾之宽,等.混凝土骨料有限元模型自动生成方法 [J].大连理工大学学报,2006,46(5):641-646. (GAO Qiao-hong,GUAN Zhen-kuan,GU Zhi-xian,etal. Automatic Generation of Finite Element Model for Concrete Aggregate[J]. Journal of Dalian University of Technology, 2006,46(5):641-646. (in Chinese)) [8]伍君勇.混凝土细观结构的自动生成[D].大连:大连理工大学,2006. (WU Jun-yong. Automatic Generation of the Mesoscopic Structure of Concrete[D]. Dalian: Dalian University of Technology, 2006. (in Chinese)) [9]马怀发.混凝土试件细观结构的数值模拟[J].水利学报, 2004, (10): 27-35. (MA Huai-fa. Meso-structure Numerical Simulation of Concrete Specimens[J]. Journal of Hydraulic Engineering, 2004, (10): 27-35. (in Chinese)) [10]张剑,金南国,金贤玉,等.混凝土多边形骨料分布的数值模拟方法[J].浙江大学学报:工学版,2004,38(5):581-585. (ZHANG Jian,JIN Nan-guo, JIN Xian-yu,etal. Numerical Simulation Method for Polygonal Aggregate Distribution in Concrete[J]. Journal of Zhejiang University (Engineering Science), 2004, 38(5): 581-585. (in Chinese)) [11]李友云,崔俊芝.具有大量椭圆颗粒/孔洞随机分布区域的计算机模拟及其改进三角形自动网格生成算法[J].计算力学学 报, 2004, 21(5): 540-545. (LI You-yun, CUI Jun-zhi. Computer Simulation Method for the Domain with Large Numbers of Random Ellipse Grains/Cavities and the Improving Automatic Triangle Mesh Generation Algorithm[J]. Chinese Journal of Computational Mechanics, 2004, 21(5): 540-545. (in Chinese)) [12]王宗敏,邱志章.混凝土细观随机骨料结构与有限元网格剖分[J].计算力学学报,2007,24(4):50-56. (WANG Zong-min, QIU Zhi-zhang. Random Aggregate Structure of Mesoscopic Concrete and Finite Element Mesh[J]. Chinese Journal of Computational Mechanics, 2007, 24(4): 50-56. (in Chinese)) (编辑:曾小汉) Modeling of Concrete’s Random Aggregate on Mesoscopic Level QU Jin, LOU Zong-ke, LIU Zhao-song (College of Water Resources and Architectural Engineering, Northwest A & F University, Yangling712100, China) Abstract:In mesoscopic sense, concrete is a three-phase composite material which is composed of aggregate, mortar and the interface layer between them. The interface layer is the weakest part of concrete, and is also the main cause of concrete’s low tensile strength. MATLAB software is used to establish three random aggregate models of circle, polygon and elliptic shape and to generate the interface layer of certain thickness. Furthermore, finite element software ABAQUS is employed to establish two-dimensional mesoscopic numerical model of concrete. Computation examples show that the algorithm is simple and the model is reliable. By introducing interface layer and grid subdivision, we provide a foundation for the numerical simulation of concrete’s damage fracture mechanism, and effectively solve the problem of connection among MATLAB, AUTOCAD and finite element software. Key words: concrete; random aggregate; tensile strength; numerical simulation; MATLAB 2015,32(04):133-1382.2 圆形骨料的投放过程
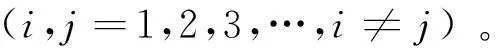
2.3 多边形骨料的生成
2.4 椭圆形骨料的生成