回归支持向量机集成模型在年径流预测中的应用

回归支持向量机集成模型在年径流预测中的应用

代兴兰

(云南省水文水资源局 曲靖分局，云南 曲靖655000)

摘要：为进一步提高径流预测精度和泛化能力，根据回归支持向量机(SVR)特性及基本原理，提出考虑不同影响因子(输入向量)的SVR集成预测模型，以云南省南盘江西桥站1961—2007年径流预测为例进行实例研究。首先，利用相关分析法选取年径流预测的若干影响因子，依次构建不同影响因子的SVR单一模型对研究实例进行预测，并构建对应的RBF模型作为对比预测模型；然后，采用加权平均和简单平均2种方法对具有较好预测精度和互补性的单一模型的预测结果进行综合集成。结果表明：基于SVR的加权平均和简单平均2种集成模型径流预测的平均相对误差绝对值分别为1.27%和1.54%，最大相对误差绝对值分别为2.99%和2.74%，其精度和泛化能力均大幅优于各单一模型以及基于RBF的加权平均和简单平均集成模型，表明加权平均SVR和简单平均SVR集成模型具有较高的预测精度和泛化能力。相对而言，加权平均集成模型赋予了预测效果好的模型更大的权重，预测精度和泛化能力均优于简单平均集成模型。预测模型和方法可为相关预测研究提供参考和借鉴。

关键词：径流预测；集成模型；回归支持向量机；加权平均；简单平均

中图分类号：P333文献标志码：A

1研究背景

提高径流预测精度对于水文预测预报具有重要意义。目前，径流预测方法主要有时间序列、回归分析、模糊模式、小波分析、集对分析等，均在径流预测预报中取得了一定的成效。但由于河川径流受多种因素的影响和制约，其预测常表现出复杂、随机、多维等特性，探寻能够有效提高径流预测精度的模型和方法一直是水文预测预报工作中的热点和难点。人工神经网络(Artificial Neural Network，ANN) 是一种模仿动物神经网络行为特征，进行分布式并行信息处理的数学模型。ANN依靠系统的复杂程度，通过调整内部大量节点之间相互连接的关系，从而达到处理信息的目的，在处理复杂、高维、非线性系统和不确定性问题方面有着广泛的应用[1]。然而，由于传统ANN算法是基于渐近理论，即当样本容量趋向于无穷大时的解决方案，在实际应用中存在着当样本容量有限时可能出现较差的推广能力、结构及参数选择困难、及收敛速度慢和易陷入局部极值等问题[2-3]。支持向量机(Support Vector Machine，SVM)是20世纪90年代中后期发展起来的基于统计学习理论构建的典型神经网络，它由Vapnik首先提出，是一种通用的前馈神经网络，用于解决模式识别和非线性映射问题。SVM具有严谨的数学基础，通过统计学习中的VC维(Vapnik-Chervonenkis Dimension)理论和寻求结构风险最小化原理来提高泛化能力，已成为继ANN之后机器学习领域新的研究热点，尤其在解决小样本容量时，很大程度上解决了传统BP在模型选择、过学习、高维和局部极值等问题，在模型识别及回归预测中有着广泛的应用[4-10]。神经网络集成(Neural Network Ensemble,NNE)是Hansen和Salamon于1990年提出的集成方法，其利用有限个神经网络对同一问题进行学习，将个体神经网络的输出以某种综合方法进行集成，集成输出的结果由各个体神经网络的输出共同决定[1,11]。实践表明，不同的预测方法往往有着不同的预测结果，不同的预测方法挖掘不同的有用信息，不同模型的预测结果通常具有互补性，其预测精度也各有差异，而没有一种适用于所有预测的通用方法。任何一种预测方法都有其适用性和局限性，应依据实际问题选择适当的模型与方法。

在实际应用中，决定预测模型精度的关键因素是问题本身的复杂程度，针对不同问题选择恰当的预测方法是决定预测效果优劣的关键。本文基于回归支持向量机(Support Vector Regression，SVR)原理及NNE基本思想，依次构建若干以不同影响因子作为输入向量的SVR单一模型分别对云南省南盘江西桥站年径流进行预测，采用加权平均和简单平均2种方法对具有较好预测精度和互补性的几种SVR单一模型的预测结果进行综合集成，为提高相关水文预测预报的精度提供模型及方法上的参考。

2SVR集成预测模型

2.1　回归支持向量机

SVM最初是为研究线性问题提出的，其用于模式识别的基本思想是通过非线性变换将输入空间变换到一个高维空间，在此新空间中通过求解凸二次规划问题，寻求最优线性分类超平面；而用于回归预测时，其基本思想不再是寻找最优分类面将样本分开，而是寻找一个最优超平面，使得所有训练样本离该最优超平面距离最短，这个超平面可看作拟合好的曲线，将SVM用于逼近函数的方法称为SVR。SVR实现回归预测步骤归纳如下[7-10,12]。

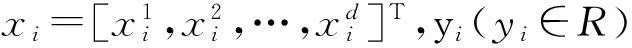
(1)

式中Φ(x)为非线性映射函数。

步骤2，定义ε线性不敏感损失函数为

(2)

式中:f(x)为回归函数返回的预测值；y为对应的真实值。

(3)

式中:C为惩罚因子，C越大表示对训练误差大于ε的样本惩罚越大;ε规定了回归函数的误差要求，ε越小表示回归函数的误差越小。求解式(3)时，同时引入Lagrange函数，并转换成对偶形式,即

(4)

式中K(xi,xj)=Φ(xi)Φ(xj)为核函数。

(5)

(6)

式中Nnsv为支持向量机个数。

步骤5，将w*和b*代入式(1)得到回归函数为

(7)

2.2　集成方法

2.2.1加权平均集成

加权平均集成是按照各单一模型预测效果的优劣给出不同的权重，然后求加权平均值，以加权平均值作为集成模型的预测值。计算公式为

(8)

(9)

式中ei为第i个模型预测相对误差的绝对值。

2.2.2简单平均集成

简单平均集成是按照各单一模型的预测值求简单平均作为最终集成模型的预测值，计算公式为

(10)

2.3　集成预测步骤

基于上述SVR基本原理和集成预测方法，SVR集成模型实现径流预测步骤可归纳如下：

(1) 利用SPSS软件选取与年径流显著相关的若干月均流量作为影响因子，确定各SVR与RBF模型的训练样本和检验样本，并对样本进行归一化处理。

(2) 基于Matlab软件环境和libsvm工具箱，依次构建不同影响因子(输入向量)的SVR单一模型及对应的RBF模型，利用训练样本对各模型进行训练及调试，率定各模型的相关参数，并利用检验样本对各模型进行预测精度及泛化能力检验。

(3) 对各SVR单一模型及对应RBF模型的预测精度及泛化能力进行分析评价，并选取若干最优模型的预测结果，采用加权平均和简单平均2种方法对预测结果进行综合集成。

(4) 对SVR集成模型预测结果进行分析。若SVR集成模型预测值达不到期望精度和泛化能力要求，则反向对各SVR单一模型进行调试和预测检验，直至SVR集成模型预测结果满足期望的精度要求。

(5) 对SVR集成模型最终预测结果进行评价分析，并与单一模型及对应的RBF集成模型的预测结果进行比较，并得出结论。

3实例应用

3.1　数据来源与分析

以云南省南盘江西桥站1961—2007年47 a的实测资料为例进行分析。利用SPSS软件分析年径流与1—11月份月均流量的相关性，分析结果见表1。

从表1可以看出，年径流与6—11月份月均流量呈显著正相关，与1—5月份月均流量无显著相关。本文选取与年径流在0.01水平(双侧)上显著相关的6—11月份月均流量作为年径流预测的影响因子，并以1961—2000年的实测资料作为训练样本，2001—2007年作为检验样本。

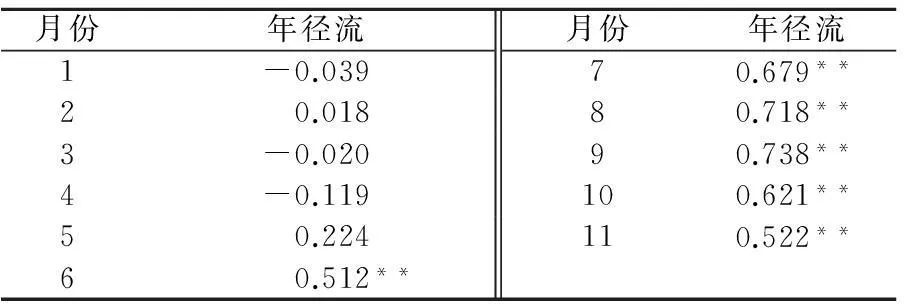
表1　年径流与1—11月份月均流量相关系数 Table 1　Coefficients of correlation between annual runoff and monthly runoff from January to November

注：“**”表示在0.01水平(双侧)上显著相关。

3.2　年径流预测的实现

3.2.1数据归一化处理

利用式(11)对各径流序列进行归一化处理。

(11)

3.2.2网络训练及模型设计

本文基于Matlab环境和libsvm工具箱，创建不同输入向量的SVR与RBF模型对南盘江西桥站47 a的实测资料进行训练和检验，各SVR与RBF模型参数的设置方法如下。

SVR模型：SVR在选定核函数条件下，模型中的惩罚因子C和核函数参数g的选取对模型的预测精度有着关键性影响。参考文献[9-10,12]，选择径向基核函数均为SVR的核函数，设置惩罚因子C和核函数参数g的搜索空间均设置为2-2～26，K取值2～5，g和C的步进大小均取0.1，不敏感系数ε均为0.001(其他参数采用默认值)，利用交叉验证法(Cross Validation,CV)确定模型中的惩罚因子C和核函数参数g。

RBF模型：在设定期望误差均为0.001条件下，编写循环训练算法程序确定RBF模型具有最佳预测效果时的径向基函数扩展速度spread。

本文从6—11月份月均流量中选取不同组合类型的月均流量为SVR与RBF模型的输入向量，年径流为输出，构建不同输入向量的SVR与RBF径流预测模型。考虑维数过低，SVR与RBF模型不能充分挖掘数据间的有用信息，因此确定SVR与RBF单一模型的输入向量维数为4～7维，并经反复调试，在下述参数设置情况下，SVR与RBF单一模型具有较好预测效果(除此之外的其他参数采用系统默认值)。各SVR与RBF单一模型的最佳参数设置见表2。

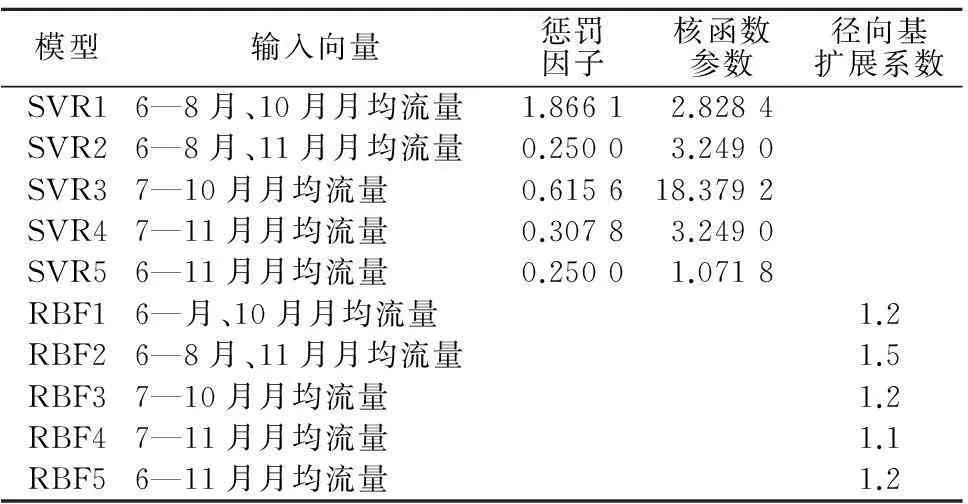
表2　各SVR与RBF单一模型最佳相关参数 Table 2　Optimum parameters of the single-models based on SVR and RBF respectively

3.3　集成预测模型权重的确定

按照上述集成预测方法和步骤，利用上述5种SVR与RBF单一模型预测样本的平均相对误差绝对值确定各自权重，结果见表3。

表3　加权平均集成模型中各SVR与 RBF单一模型权重表 Table 3　Weights of single-models in the weighted average model based on SVR and RBF respectively

3.4　预测结果及分析

利用上述训练好的5种SVR模型及对应的RBF模型分别对云南省南盘江西桥站2001—2007年年径流进行预测，结果见表4；并利用加权平均、简单平均集成方法对SVR与RBF单一模型的预测结果进行综合集成，结果见表5。

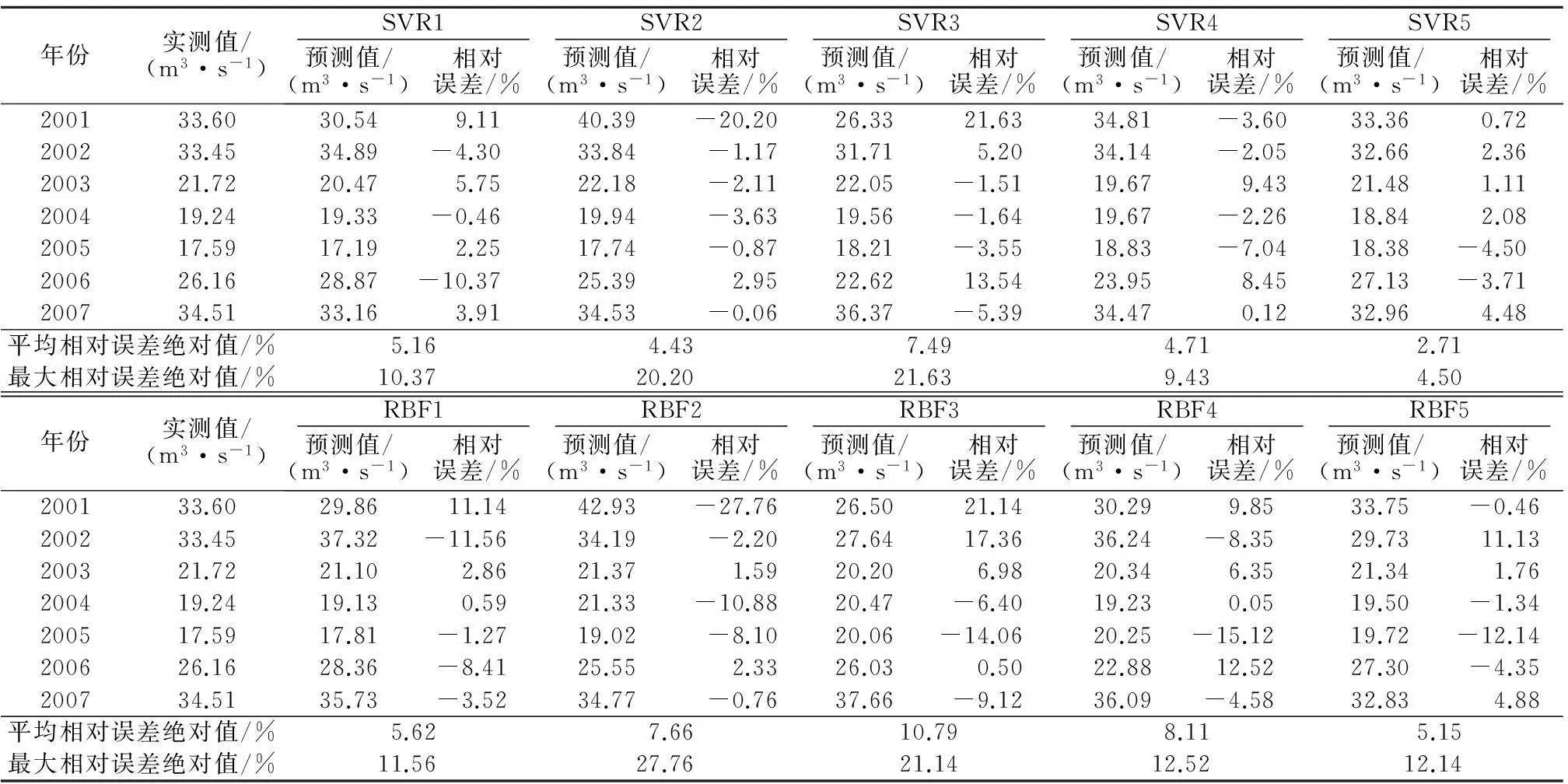
表4　西桥站2001—2007年各单一模型径流预测结果及比较 Table 4　Comparison of the runoff prediction results of each single model for west bridge station from 2001 to 2007

表5　西桥站2001—2007年SVR与RBF集成模型径流预测结果及比较 Table 5　Comparison of the runoff prediction results between SVR and RBF ensemble models for west bridge station from 2001 to 2007

分析上述诸表可以得出以下结论：

(1) 从表4可以看出，各SVR单一模型的平均相对误差绝对值、最大相对误差绝对值均优于相对应的各RBF单一模型，表明SVR模型具有较好的预测精度和泛化能力，尤其在小样本情况下，SVR模型的预测精度和泛化能力是RBF所不可比拟的。从SVR单一模型的预测结果来看，其预测的平均相对误差绝对值在2.71%～7.49%之间，这一定程度上均能满足径流预测的实际应用需求。

(2) 从表4各单一模型的预测结果来看，凡输入向量(影响因子)中有第11月月均流量的单一模型的预测效果(除RBF2模型)均要优于其他单一模型，表明11月份月均流量对于各SVR与RBF单一模型的预测效果有着重要影响。

(3) 从表5可以看出，加权平均SVR集成模型与简单平均SVR集成模型的平均相对误差绝对值分别为1.27%和1.54%，最大相对误差绝对值分别为2.99%和2.74%，精度和泛化能力均大幅优于各单一模型以及加权平均RBF集成模型与简单平均RBF集成模型，表明集成模型和集成方法用于径流预测是合理可行的。集成模型融合了各单一模型预测结果的互补性，有效提高了径流预测的精度和泛化能力。相对而言，加权平均集成模型赋予了预测效果好的模型更大的权重，预测精度和泛化能力要优于简单平均集成模型。

4结语

NNE早在1990年就由Hansen和Salamon提出，但由于目前仍没有较成熟的理论和方法来选定差异较大的个体网络以及评价多个网络之间的差异度(互补性)，这在很大程度上制约了NNE在实际中的应用。本文基于SVR原理和NNE的基本思想，利用不同输入向量(不同维数)的方法构建5种SVR单一模型，采用加权平均和简单平均2种集成方法构建SVR集成模型对云南省南盘江西桥站后7 a年径流预测进行实例验证。验证结果表明，SVR集成模型具有较高的预测精度和泛化能力，是提高径流预测精度的有效方法。

参考文献：

[1]田景文,高美娟.人工神经网络算法研究及应用[M].北京：北京理工大学出版社,2006. (TIAN Jing-wen, GAO Mei-juan. Artificial Neural Network Algorithm： Research and Application [M]. Beijing: Beijing Institute of Technology Press, 2006.(in Chinese))

[2]田雨波.混合神经网络技术[M].北京：科学出版社,2009. (TIAN Yu-bo. Hybrid Neural Network Technology [M]. Beijing: Science Press, 2009.(in Chinese))

[3]王雷.支持向量机在汽轮机状态监测中的应用[M].北京：北京师范大学出版社,2012. (WANG Lei. Application of Support Vector Machine to the Monitoring of Steam Turbine[M]. Beijing: Beijing Normal University Press, 2012. (in Chinese))

[4]张楠,夏自强,江红.基于多因子量化指标的支持向量机径流预测[J].水利学报,2010,41(11):1318-1323. (ZHANG Nan, XIA Zi-qiang, JIANG Hong. Prediction of Runoff Based on the Multiple Quantity Index of SVM[J]. Journal of Hydraulic Engineering, 2010, 41(11): 1318-1323. (in Chinese))

[5]肖浩波,谷艳昌.混凝土坝安全监控最小二乘支持向量机模型[J].长江科学院院报,2013,30(5):34-37. (XIAO Hao-bo, GU Yan-chang. Monitoring Model for Concrete Dam Safety Using Least Square Support Vector Machine[J]. Journal of Yangtze River Scientific Research Institute, 2013, 30(5): 34-37. (in Chinese))

[6]李代华,崔东文. 相空间重构支持向量机在径流模拟中的应用研究[J].长江科学院院报,2013,30(10):21-26. (LI Dai-hua, CUI Dong-wen. Phase Space Reconstruction of Support Vector Machine in Runoff Simulation[J]. Journal of Yangtze River Scientific Research Institute, 2013,30 (10): 21-26. (in Chinese))

[7]李波,刘明军,马奕仁,等.基于平均曲率模态和最小二乘支持向量机的混凝土拱坝损伤识别方法研究[J].长江科学院院报,2013,30(11):113-118. (LI Bo, LIU Ming-jun, MA Yi-ren,etal. Damage Identification of Concrete Arch Dam Using Mean Curvature Mode and Least Squares Support Vector Machine [J]. Journal of Yangtze River Scientific Research Institute, 2013,30 (11): 113-118. (in Chinese))

[8]徐飞,徐卫亚,刘大文,等.洞室围岩变形预测的ACA-LSSVM模型及工程应用研究[J].长江科学院院报,2009,26(2):32-35. (XU Fei, XU Wei-ya, LIU Da-wen,etal. ACA-LSSVM for Deformation Forecasting of Cavern Surrounding Rock and Its Application[J]. Journal of Yangtze River Scientific Research Institute, 2009,26 (2): 32-35. (in Chinese))

[9]崔东文. 支持向量机在湖库营养状态识别中的应用研究[J].水资源保护,2013,29(4):26-30. (CUI Dong-wen. Application of Support Vector Machine to Lake and Reservoir Trophic Status Recognition[J]. Water Resource Protection, 2013,29 (4): 26-30. (in Chinese))

[10]崔东文.支持向量机在水资源类综合评价中的应用研究——以全国31个省级行政区水资源合理性配置为例[J].水资源保护,2013,29(5):20-27. (CUI Dong-wen. Support Vector Machine for Comprehensive Evaluation of Water Resources: Application to Reasonable Allocation of Water Resources in 31 Provincial-level Administrative Regions in China[J]. Water Resource Protection, 2013,29 (5): 20-27. (in Chinese))

[11]SOLLICH P, KROGH A. Learning with Ensemble: How Over-fitting Can be Useful[M]. Cambridge: MIT Press, 1996: 190-193.

[12]史峰,王辉,郁磊,等. MATLAB智能算法30个案例分析[M].北京:北京航空航天大学出版社,2011. (SHI Feng, WANG Hui, YU Lei,etal. MATLAB Intelligent Algorithm: 30 Case Analysis [M]. Beijing: Beihang University Press, 2011. (in Chinese))

(编辑：赵卫兵)

Application of SVR Ensemble Model to Annual Runoff Forecasting

DAI Xing-lan

(Qujing Branch of Yunnan Hydrological and Water Resource Bureau, Qujing655000, China)

Abstract:An ensemble model involving different impact factors (input vectors) based on support vector regression (SVR) is put forward to improve runoff prediction accuracy and generalization ability. The runoff at Nanpanjiang west bridge station in Yunnan from 1961 to 2007 is taken as a case study. First, a number of impact factors for annual runoff forecast are selected to build different models for the study of a single instance of SVR, and the corresponding RBF models are built as a comparison. In subsequence, the results of single models (which are accurate and complementary) are integrated by using weighted average and simple average respectively. Results showed that: the average relative absolute error of weighted average and simple average ensemble model based on SVR was respectively 1.27% and 1.54%, and the maximum relative absolute error is 2.99% and 2.74%. The accuracy and generalization capabilities are significantly superior to the single models as well as the weighted average and simple average ensemble model based on RBF models. The weighted average ensemble model based on SVR has better accuracy and generalization capability than simple average because it gives more weight to the models with good prediction result.

Key words:runoff forecasting; ensemble model; SVR; weighted average; simple average