基于一维漂移流模型的并联矩形双通道密度波流动不稳定性数值模拟

基于一维漂移流模型的并联矩形双通道密度波流动不稳定性数值模拟

熊万玉，唐瑜*，陈炳德

(中国核动力研究设计院，四川 成都610041)

摘要：基于一维漂移流模型构建了并联矩形双通道密度波流动不稳定性数学模型。模型中采用Zuber推荐的经验关系式计算两相流体空泡份额，采用Chisholm关系式和中国核动力研究设计院自拟关系式计算两相流体的摩擦压降。求解过程中将质量方程、能量方程与动量方程解耦，并在计算域内沿流动方向依次求解方程组。计算过程中，首先开展稳态计算，在稳态解的基础上，通过添加流量或功率扰动，诱发流体周期性振荡，通过辨识瞬态计算中得到的流量振荡模式来获得流动不稳定边界。采用数值计算获得的密度波脉动图像与实验中观察到的密度波脉动现象的特征基本一致。最后，针对16组典型实验工况开展数值模拟，结果表明，大部分工况下计算不稳定界限热流密度与实验值的相对偏差小于±20%。

关键词：并联矩形双通道；密度波不稳定性；漂移流模型；数值模拟

中图分类号：TK124 文献标志码：A

收稿日期：2014-08-01;修回日期：2014-11-05

作者简介：熊万玉(1973—)，女，湖北公安人，研究员，硕士，从事反应堆热工水力研究

doi：10.7538/yzk.2015.49.11.1989

*通信作者：唐瑜，E-mail: tangyu614@hotmail.com

Numerical Simulation on Density Wave Oscillation in Parallel Twin

Rectangular Channels Based on One-dimensional Drift Flux Model

XIONG Wan-yu, TANG Yu*, CHEN Bing-de

(NuclearPowerInstituteofChina,Chengdu610041,China)

Abstract:A mathematical model was proposed for the density wave oscillation in parallel twin rectangular channels based on one-dimensional drift flux model in this paper. In the model, an empirical correlation recommended by Zuber was applied to calculate the void fraction of two-phase flow. Chisholm correlation and the correlation developed by NPIC were used for the prediction of the frictional pressure drop of two-phase flow. During the process of solving, mass, momentum and energy balance equations were decoupled and solved along the flow direction successively in the whole computational domain. The steady state calculation was made at first, then the periodical oscillation of flow was induced by adding small flow rate or heating power disturbance to the steady state solution. The flow instability boundary can be obtained by checking the oscillation mode in transient calculation. The calculation results indicate that the flow oscillations obtained through simulation have the same characteristics as those observed in the experiment. At last, the simulation were made for sixteen typical cases chosen from the experiment, and the results indicate that the relative differences between the calculated flow instability boundary heat flux and the corresponding experimental data are no more than ±20% for most part of cases.

Key words：parallel twin rectangular channels; density wave oscillation; drift flux model; numerical simulation

两相流动不稳定性是反应堆热工水力研究的重要课题之一，它涉及到反应堆设计、运行、维护等多个方面的内容。根据流量变化方式不同，流动不稳定性可分为静态流动不稳定性和动态流动不稳定性。静态流动不稳定性是指流量由一个值变化到另一个值，出现新的工况，且系统仍维持在新工况下工作。动态流动不稳定性多是指有固定频率的脉动现象，系统进口流量围绕一平均值可能呈现收敛的、发散的或稳定的脉动变化[1]。密度波流动不稳定性是反应堆中最为常见的动态不稳定性之一，它与流量、密度以及压降三者之间的相互作用有关。由于密度波不稳定性对反应堆设计及安全运行有重要影响，迄今为止，研究者已针对密度波脉动问题开展了大量的实验和理论研究。就理论研究而言，主要可分为时域法和频域法两大类，本文所开展的流动不稳定性数值模拟属于时域分析法。时域法一般从两相流解析数学模型开始，建立守恒方程组。然后把非线性方程组进行有限差分离散，进行数值计算。从预设初始条件开始，计算流量、压差、温度等物理量随时间的变化，来判断预设的初始工况下是否会发生流动不稳定。采用时域法进行流动不稳定性研究的学者很多，早在1963年，Meyer等[2]就采用欧拉方法建立了守恒方程，并利用有限差分方法在时域内求解方程组。在他们的模型中，整个系统是一个两端压力固定的沸腾流道。1982年，Dogan等[3]运用集总参数法对垂直沸腾两相流动单管内的压力降型脉动进行了数值求解。1990年，Lecoq等[4]利用时域法对蒸汽发生器内密度波型脉动进行了数值计算，通过两相驻留时间，分析了延迟效应对密度波型脉动的影响，另外还分析了极限环振荡。黄军等[5]以一维漂移流模型为基础，对管间脉动建立了计算模型，采用C语言和SIMPLER算法编制了程序，并调试通过。李虹波[6]以圆管平行双通道管间脉动理论模型为基础，针对矩形通道进行修正，表征出矩形双通道内管间脉动的动态行为。夏庚磊等[7]采用RELAP5程序对垂直并联管中气液两相流动不稳定性实验装置进行模拟，并与实验结果对比，发现计算结果与实验结果符合较好。

本文基于一维漂移流模型构建并联矩形双通道密度波流动不稳定性数学模型，给出该模型的数值求解方法，选定16组计算工况开展流动不稳定性数值模拟，获得各工况下流动不稳定的界限热流密度，绘制相应的流动不稳定边界，并与实验数据进行对比。

1数学物理模型

图1　并联双通道几何模型 Fig.1　Geometry model of parallel twin channels

1.1几何模型

并联双通道的几何结构如图1所示。图1中，两个结构完全相同的矩形通道分别与上下联箱相连接后构成并联通道，在联箱内部流体的压力相等。流体从下联箱进入装置后分别经由两个通道垂直向上流动，在流动过程中受到管壁的加热后从单相过冷水变为气液两相混合物，最终汇集到上联箱中。流道沿轴向依次为入口段、加热段和上升段，其中入口段和上升段均设有节流件模拟体，以模拟实际管路中的阀门、弯头等装置带来的节流效应。通道基本几何参数列于表1。

表1　并联双通道基本几何参数

1.2基本假设

本文中，数学模型的构建基于下述假设：1) 流动是一维的；2) 两相流动传热采用漂移流模型；3) 两个实验段进出口之间的压差相等；4) 沿轴线方向计算流体的物性参数时，均以进口压力为基准；5) 热负荷沿管长均匀分布；6) 忽略加热管壁热容。

其中，假设2涉及到两相模型的选择，漂移流模型曾被多数研究者使用，其有效性得到了充分验证。假设4的提出是考虑到管间压差远低于运行压力，因此在物性计算时将整个通道的压力视为一致。假设5的提出是为了与实验条件保持一致，便于对数值模拟结果进行验证。

1.3数学模型

本文中，数学模型主要包括单相和两相基本守恒方程，以及用以封闭方程组的本构关系式和两相摩阻经验关系式。

1) 单相守恒方程组

(1)

(2)

(3)

(4)

式中：ρ为流体密度；u为流体速度；p为压力；f为流体的摩阻系数；De为等效直径；h为流体焓；q为热流密度；g为重力加速度。

2) 两相守恒方程组

(5)

(6)

(7)

本构关系式：

(8)

3) 空泡份额和两相摩阻经验关系式

在模型中，空泡份额采用Zuber推荐的经验关系式进行计算，空泡份额的分布系数C0采用针对矩形通道的关系式计算。在12 MPa以下，采用Chisholm两相摩阻关系式，在12～16 MPa压力范围内，采用中国核动力研究设计院自拟关系式，此自拟关系式是针对高压条件下矩形通道两相摩阻提出的。

(1) Zuber空泡份额关系式[8]

(9)

式中：x为热平衡干度；C0=1.4-0.4p/pcr，pcr为临界压力。

(2) Chisholm两相摩阻关系式[8]

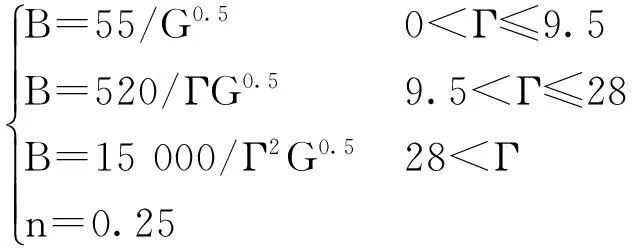
(10)

式中，Γ为Chisholm数。

(3) 中国核动力研究设计院自拟高压矩形通道两相摩阻关系式[9]

(11)

式(11)的适用范围为：12.1～15.7 MPa，520～2 500 kg/(m2·s)。

2模型求解

2.1网格划分及微分方程组的离散

本文采用等长度的计算控制体对计算区域进行网格划分，速度、焓、密度等物理量均位于控制体的中心。经网格无关性分析，采用1 mm与0.5 mm网格时，对同一工况计算获得的不稳定界限功率的相对偏差不超过2%，故将每个控制体的空间步长设为1 mm，时间步长设为0.01 s，如图2所示。基于时间和空间网格，对式(1)～(7)进行差分离散，可获得单相和两相守恒方程的差分方程组。其中，对流项的差分采用一阶迎风差分格式。

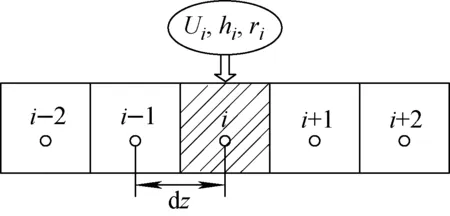
图2　网格划分方法 Fig.2　Method of mesh division

2.2数值求解方法

数值求解的基本流程如图3所示。根据流程图，首先应求出给定热工工况下的稳态解，然后将稳态解作为瞬态计算的初始条件，引入扰动后展开瞬态计算。根据瞬态计算的结果，结合相应的判定准则，判断流动不稳定是否发生，并决定是否需要改变加热功率继续运算。

图3　数值求解基本流程 Fig.3　Flow path of numerical solving

1) 小扰动的添加方法

在稳态计算完成之后、瞬态计算开始之前，需引入外加小扰动来打破流动传热的平衡，以观察系统对扰动的响应，从而判断该参数下系统是否会发生流动不稳定。引入扰动的方法有两种，一是流量扰动，二是功率扰动。

流量扰动的实施方法：假设某通道(如通道1)入口流量W在t=0时刻发生了一个有限幅值的扰动，由W1变为W1+δW，由于总入口流量不变，通道2的流量由W2变为W2+δW，且在t=Δt时刻，扰动消失。

功率扰动的实施方法：假设在t=0时刻，功率发生了偏离稳态的有限幅值的扰动，由Q变为Q′，并在持续一段时间(通常设为1 s)后，恢复至原功率。

2) 瞬态计算内迭代中方程组的求解策略

目前，针对二维以上流动传热问题的数值计算，较成熟的求解方法有SIMPLE系列算法、PISO算法以及由两者结合而成的SIMPISO算法等。这些算法大都将质量、动量和能量方程耦合在一起，并对计算域内所有方程组联立求解。对于一维流动传热问题，微分方程组被简化为抛物型方程，因此一方面可将质量、能量方程与动量方程解耦，即在每一时层的内迭代计算中，先求出满足连续性方程和能量方程的解，在内迭代收敛后，再根据已求得的速度和焓来计算压降；另一方面，无需对全场方程组联立求解，而是采用图4所示的沿流动方向依次求解方程组。每完成一次从入口到出口的求解称为一轮迭代，每一轮迭代之前，首先假设计算区域内的密度场分布，若一轮迭代之后，新求解得到的密度场与假设的密度场足够接近(满足收敛条件)，则认为获得了满足连续性方程和能量方程的解，否则，从入口开始进行下一轮迭代，直到满足收敛条件。

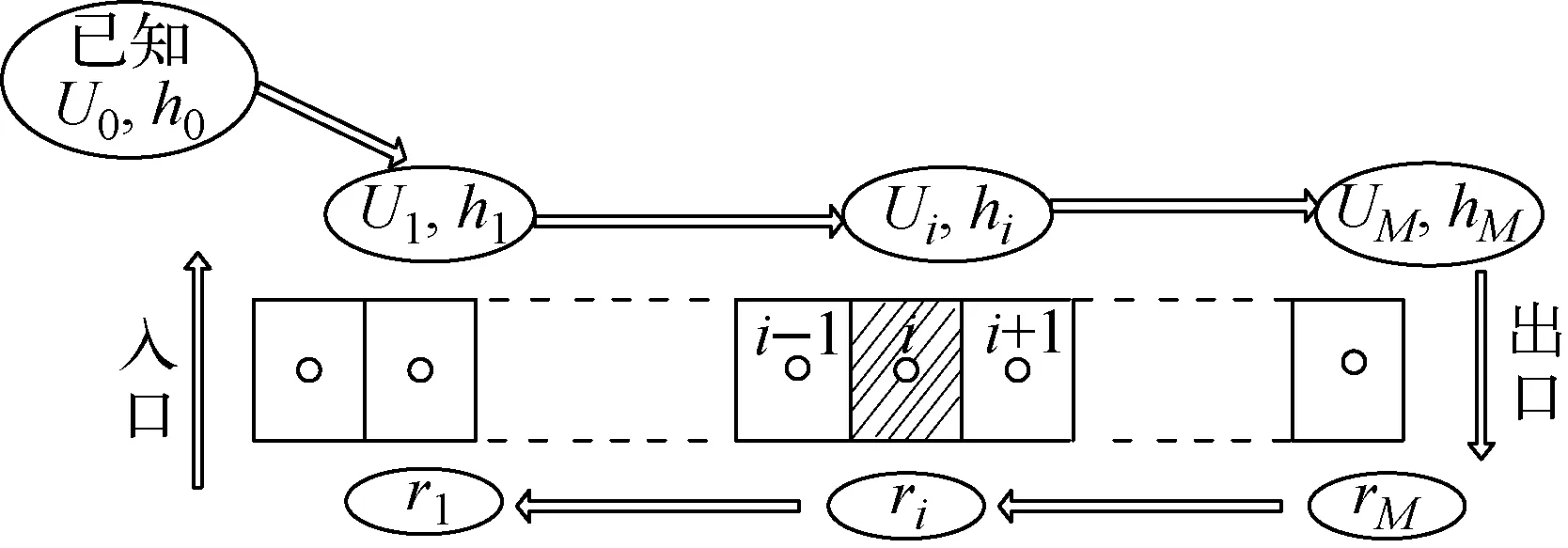
图4　求解方程组的次序 Fig.4　Order to solve equations

3) 微分方程组的离散及求解

将偏微分方程组在时间和空间节点上离散，得到差分方程组。

单相区的差分方程组为：

(12)

(13)

(14)

两相区的差分方程组为：

(15)

(16)

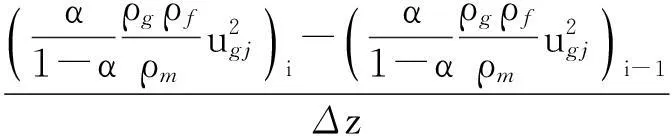
(17)

方程迭代顺序如图4所示，具体求解步骤如下：

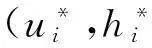
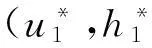
(3) 用计算出的流体焓(hi)和系统压力更新整个区域内各节点的流体物性(ρi，μi)。

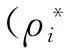
(5) 将通过步骤1～4求解出的满足连续性方程和能量守恒方程的速度(ui)、密度(ρi)和焓(hi)，代入动量守恒方程计算出各节点之间的压降(Δpi)，再对分压降求和以获得流体在整个流域上的总压降。

4) 流量的动态分配

上述算法是针对单个通道的，对于并联通道中的各分通道，在计算的任意时刻入口焓是恒定且已知的，但入口速度却是随时间变化的，若无法确定入口速度，则内迭代就无法按照前文描述的方式进行。欲计算分通道入口流速，需利用两个边界条件，一是流量边界条件，即入口总流速恒定且已知，二是压力边界条件，即并联通道的分通道总压降相等。

基于上述边界条件，可采用下述方法求解并联通道流量动态分配问题。

(1) 令p′=Δp1-Δp2，则p′为入口流量的函数，可记为p′(W1，W2)，又由于W1+W2=W，W为已知量，则p′(W1，W2)可变为p′(W1)。

(2) 令W(n)为第n次迭代值，则由弦截法可得：

(18)

又知p′(W1(n))=0，因此，可得：

(19)

(3) 反复迭代，直至p′(W(n))<ε，取W1=W1(n)、W2=W-W1。

5) 流动不稳定的判断方法

实验中通过观察流量脉动幅值是否放大来判断流动不稳定是否发生，在数值模拟中，也可采用相似的方法来寻找流动不稳定边界。事实上，在计算过程中，无论热流密度是否达到发生流动不稳定的界限热流密度，当小扰动被引入后，入口流量都会出现周期性振荡，不同之处在于振荡幅值是逐渐衰减、不断放大还是恒定不变。显然，脉动幅值逐渐减小意味着流量振荡终会消失，流动仍处于稳定状态，脉动幅值不断放大意味着流动已失稳，而流量呈等幅振荡则标志着流动正处于稳定和失稳的边界，在这种情况下所获得的热流密度即为流动不稳定界限

热流密度。

3计算结果

3.1流动不稳定基本现象

通过数值模拟，获得了入口流量振荡的基本图像，如图5所示。并联通道中发生的是典型的周期性异相脉动，且由振荡模式的不同可分辨出图5中流动分别处于稳定、失稳和不稳定边界。

图6示出流动失稳后入口流量与进出口压降的瞬时变化情况。可看出，各分通道的入口压降与各自通道入口流量的变化同相，而出口压降则与各自通道入口流量的变化反相。这与通过实验所获得的结论完全一致。

3.2不稳定界限热流密度及不稳定边界计算

表2为所选择的16组热工工况，均来自并联矩形双通道密度波流动不稳定性实验[10]，实验中所采用矩形通道的基本几何参数与表1中完全一致。实验参数范围为：系统压力，3～14 MPa；质量流速，400～800 kg/(m2·s)；入口过冷度，5～120 ℃。

a——幅值衰减(流动稳定)；b——幅值放大(流动失稳)；c——等幅振荡(不稳定边界) 图5　流量振荡的3种模式 Fig.5　Three oscillation modes of flow

图6　流动失稳后入口流量与进出口压降的瞬时变化 Fig.6　Transient variation of inlet flow and pressure drop at inlet and exit of channel during flow oscillation

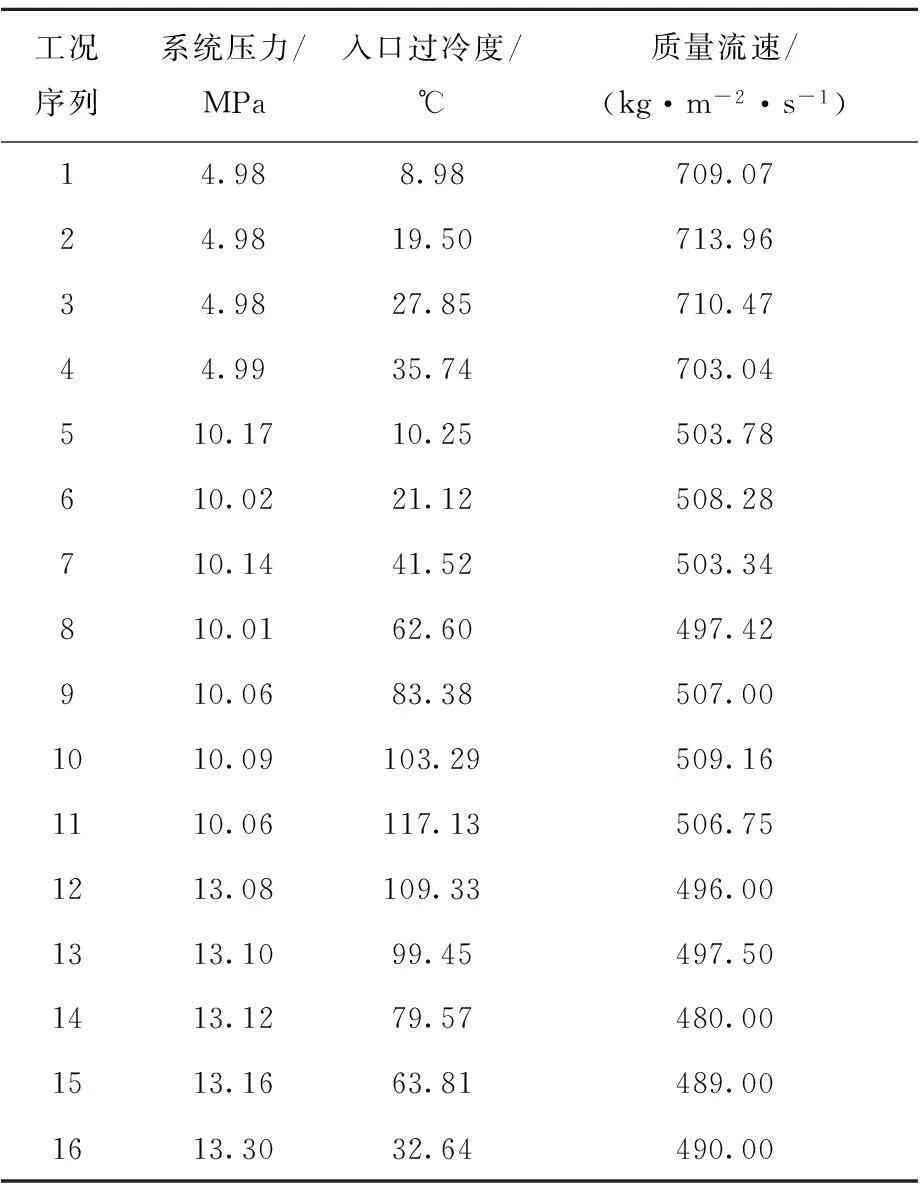
表2　计算工况

通过计算，获得了16组工况的不稳定界限热流密度，并与实验数据进行了对比，具体结果列于表3。从表3可见，除工况1和工况5外，其余工况下流动不稳定界限热流密度的计算值与实验值的相对偏差在±20%以内，说明数值计算的结果具有一定的准确性。此外，从表3还可看到，在13 MPa的系统压力下，计算相对偏差小于±6%，这是因为在高压下采用了针对矩形通道的两相摩擦压降关系式之故。

按式(14)、(15)将表2、3中热工参数整理成过冷度数Nsub和相变数Npch，获得了不同压力下的计算流动不稳定边界，其中流动不稳定边界采用Isshi[11]推荐的过冷度数-相变数空间进行描述，如图7所示。与通过实验获得的流动不稳定边界相比，计算不稳定边界在13 MPa下与实验值吻合较好；10 MPa下，计算值与实验值在低过冷度区域吻合较好，在高过冷度区域则偏差较大，且随着过冷度的增加有放大趋势；5 MPa下，计算不稳定边界偏保守。

表3　不稳定界限热流密度计算值与实验值的对比

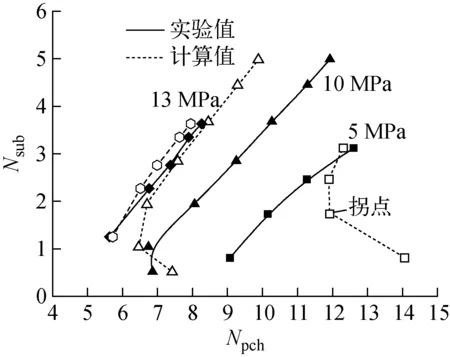
图7　不稳定边界计算值和实验值对比 Fig.7　Comparison between calculated flow instability boundary and experimental data

(20)

(21)

式中：Δhsub为入口欠焓；Δρfg为气液相密度差；Ah为加热面积；A为流通面积。

综上可知，数值模拟的计算结果在高压下与实验值吻合得更好。这是因为在12 MPa以上的工况下采用了针对矩形通道的摩阻关系式，而在对12 MPa以下工况进行计算时，由于缺乏相应的矩形通道两相摩阻关系式，而采用了基于圆管的经验关系式，使得计算结果与实验结果存在偏差。

4结论

本文基于一维漂移流模型构建了并联双通道密度波流动不稳定性数学模型。模型中采用Zuber推荐的经验关系式计算流体空泡份额，分别采用Chisholm关系式和中国核动力研究设计院自拟关系式计算12 MPa以下和12 MPa以上两相流体的摩擦压降。通过数值模拟，获得了与实验现象特征一致的密度波脉动图像。选择16组实验工况进行数值模拟，计算结果表明，在所有选择计算工况中，除个别工况外，通过计算获得的流动不稳定界限热流密度与实验值的相对偏差小于±20%。尤其是在13 MPa下，其相对偏差小于±6%，这表明，采用本文构建的数学模型和提出的数值求解方法可对并联矩形双通道流动不稳定性进行较为准确的模拟。

参考文献：

[1]鲁钟琪. 两相流与沸腾传热[M]. 北京：清华大学出版社，2002.

[2]MEYER J, ROSE R. Application of a momentum integral model to the study of parallel channel boiling flow oscillations[J]. J Heat Transfer, 1963, 85(1): 1-9.

[3]DOGAN T, KAKAC S, VEZIROGLU T N. Lumped parameter analysis of two-phase flow instabilities[C]∥Proceedings of the 7th International Heat Transfer Conference. Munchen: [s. n.], 1982: 213-218.

[4]LECOQ G, METAICH M, SLASSI-SENNOU M. A simple model for the study of dynamic instabilities[J]. Nuclear Engineering and Design, 1990, 122: 41-52.

[5]黄军，黄彦平，王飞. 两管平行通道管间脉动建模及程序编制[C]∥中国工程热物理学会多相流学术会议年会论文集. 成都：中国工程热物理学会，2004：157-162.

[6]李虹波. 矩形双通道流动不稳定性基础研究[D]. 成都：中国核动力研究设计院，2006.

[7]夏庚磊，郭赘，彭敏俊. 基于RELAP5的两管平行通道流动不稳定性研究[J]. 原子能科学技术，2010，44(6)：694-700.

XIA Genglei, GUO Yun, PENG Minjun. Investigation on two-phase flow instability in parallel channels based on RELAP5 code[J]. Atomic Energy Science and Technology, 2010, 44(6): 694-700(in Chinese).

[8]徐济鋆，贾斗南. 沸腾传热和汽液两相流[M]. 北京：原子能出版社，1993.

[9]洪钢. 矩形通道两相摩阻实验研究[R]. 成都：中国核动力研究设计院，2009.

[10]唐瑜. 并联矩形双通道第一二类密度波流动不稳定性研究[D]. 成都：中国核动力研究设计院，2014.

[11]ISHII M. Thermal induced flow instabilities in two-phase mixtures in thermal equilibrium[D]. Georgia, US: Georgia Institute of Technology, 1971.