基于最快衰减余弦窗全相位FFT的电力谐波分析

基于最快衰减余弦窗全相位FFT的电力谐波分析

蔡晓峰1，熊欣2

(1.河南工程学院 机械工程学院，河南 郑州 451191；

2.河南工程学院 电气信息工程学院，河南 郑州 451191)

摘要：傅里叶变换是电力谐波分析的常用算法，但在非同步采样情况下会出现频谱泄漏，从而影响谐波分析的精度.为抑制频谱泄漏，提出了基于最快衰减余弦窗全相位FFT的电力谐波分析方法.该方法将最大旁瓣衰减速率余弦窗与全相位频谱分析技术相结合，利用前者旁瓣衰减快与后者泄漏抑制能力强的双重优势实现谐波分析，推导了方便实用的谐波幅值校正公式，通过仿真测试，验证了该算法抑制频谱泄漏的能力强、谐波分析的精度高.

关键词：全相位；快速傅里叶变换；窗函数；插值；谐波分析

中图分类号：TM935文献标志码：A

收稿日期：2015-01-05

作者简介：蔡晓峰(1981-)，女，河南永城人，讲师，硕士，主要研究方向为数字信号处理.

电力谐波一般指电力系统电压或电流中所含有的频率为基波整数倍的电量成分，通常是由非线性负载产生的.谐波对电力系统的危害十分严重，比如谐波使电能的生产、传输和利用效率降低，使电气设备过热、产生振动和噪声、绝缘老化、使用寿命缩短甚至发生故障或烧毁，谐波还会引起继电保护和自动装置误动作，使电能计量出现混乱[1].因此，对电力系统中的谐波进行准确测量，确切掌握谐波的实际状况，对于防止谐波危害、维护电网的安全经济运行是十分必要的.在工程实践中，通常采用快速傅里叶变换(Fast Fourier Transform，FFT)进行谐波分析，但在FFT中非同步采样所引起的频谱泄漏会影响频谱分析精度，通常采用加窗和频谱校正法对FFT谱计算结果进行处理[2]以降低频谱分析的误差.文献[3]在此基础上，对数据截断方式进行改进，提出了一种全相位(all-phase)FFT频谱分析方法，即apFFT，文献[4]证明了该算法具有优良的泄漏抑制能力.随后出现的apFFT相位差校正法[5]被应用于机械测试[6]、频率测量[7]等领域.但全相位FFT频谱分析理论上仍然受到频谱泄漏的影响，故施加良好的窗函数对抑制泄漏、提高频谱分析的精度至关重要.为此，将性能优良的最大旁瓣衰减速率窗(Maxium Side Lobe Decay Speed Windows，简称MSLD窗)[8]引入全相位FFT频谱分析中，推导了相应的幅值校正公式，通过仿真测试，验证了该算法抑制频谱泄漏的能力强且谐波分析的精度高.

1apFFT频谱分析原理简介

N阶全相位频谱分析过程如图1所示.从图1可看出，只需用长为2N-1的卷积窗wc对中心样点x(0)前后2N-1个数据进行加权，然后对两两间隔为N的加权数据进行重叠相加形成N个数据，再作点数为N的FFT即可得全相位谱分析结果.其中，图1中的卷积窗由前窗f与翻转的后窗b卷积而成，即

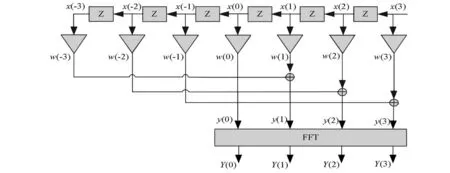
图1　N阶全相位FFT谱分析基本框图(N=4) Fig.1　Block diagrams of N-order all-phase FFT spectrum analysis(N=4)

wc(n)=f(n)*b(-n)，n=[-N+1,N-1].

(1)

若f=b=RN(RN为矩形窗)，则称为无窗全相位频谱分析；若f和b中其一为RN，则称单窗全相位频谱分析；若f=b≠RN，则称为双窗全相位频谱分析.其中,双窗全相位频谱分析比无窗全相位频谱分析具有更好的频谱泄漏抑制能力，应用较多.

图1中，若输入信号为单一频率信号，则

x(n)=ej(ωn+θ0) ，n∈[0,N-1].

(2)

由文献[4-5]可知，双窗apFFT输出的频谱

Y(k)=|X(k)|2ejθ0，k=0,1,2,…,N-1,

(3)

其中,X(k)为信号x(n)加f窗FFT的频谱,即双窗apFFT输出的幅度谱为传统加窗FFT幅度谱的平方.这种关系使旁瓣谱线相对于主谱线的比值也按照平方衰减，使主谱线更为突出，所以apFFT具有优良的频谱泄漏抑制性能.此外,apFFT的相位谱为中心样点x(0)的理论相位值，该相位值不受频偏影响，不用校正，即apFFT具有“相位不变性”且相位精度很高，这是用全相位频谱分析进行参数校正的基础.

2apFFT时移相位差法

apFFT相位差法与传统FFT相位差法原理类似，都是利用两段一定间隔的数据段间的相位关系校正信号参数.考虑对区间[-N+l，N-1]进行apFFT，取apFFT主谱线上的相位值可得中心样点x(0)的相位,记为φ0.若将采样序列延迟L个采样间隔，显然这时序列的中心样点也会有大小为L的相移，对延时后的序列再做apFFT.根据前面阐述的apFFT的“相位不变性”，取apFFT主谱线上的相位值φ1，则

φ1=φ0-ΩL×Ts.

(4)

可得模拟角频率Ω的估计式:

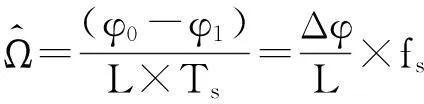
(5)

对应数字角频率

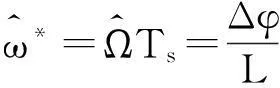
(6)

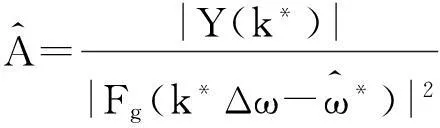
(7)

其中,Fg(ω)为双窗apFFT频谱分析中所采用的窗函数的幅度谱.

3基于MSLD窗的双窗apFFT频谱校正算法

apFFT使用的窗函数对其频谱泄漏抑制能力有重要影响，在众多窗函数当中，文献[8]提出的MSLD窗是相同项数的组合余弦窗中旁瓣衰减速率最快的，具有优良的抑制频谱泄漏的能力.将MSLD窗与全相位FFT结合，能够获得很好的频谱分析效果.表1反映了这些MSLD窗的频谱特性.

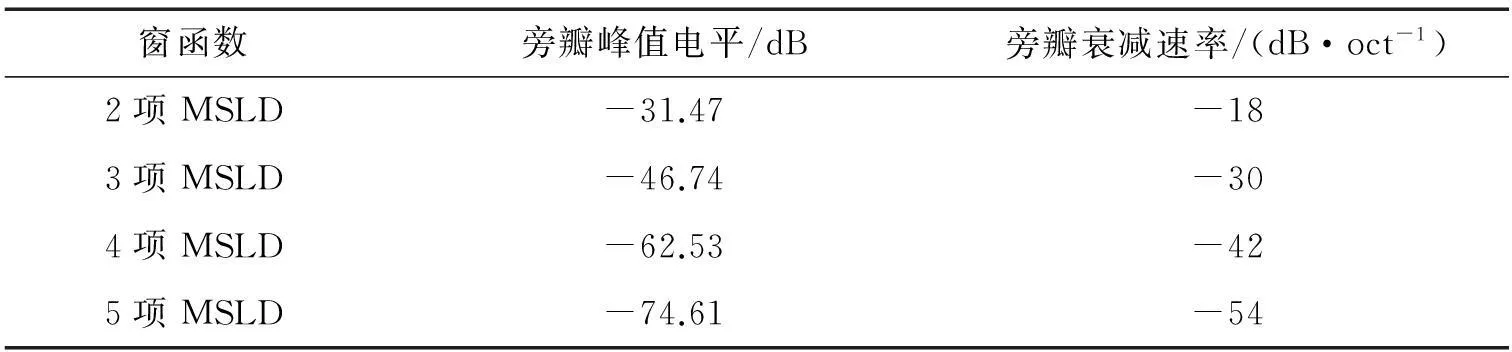
表1　MSLD窗的旁瓣特性 Tab.1　The sidelobe characteristic of the MSLD windows

从表1可以看出，项数越大的MSLD窗旁瓣峰值电平越低、衰减速率越快，但窗函数主瓣也会变宽、频谱分辨能力变差.在电力谐波分析中，选择3项和4项MSLD窗较为合适，因为两者不但具有较快的旁瓣衰减速率，而且主瓣也不过宽.

为了利用MSLD窗进行全相位频谱分析，首先需要分析窗函数的频谱，如下式所示的余弦组合窗:

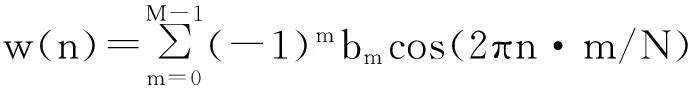
(8)

其中，M为窗函数的项数；N为窗函数的点数，n=0，1，2，…，N-1； bm为余弦项系数，其频谱[9]为

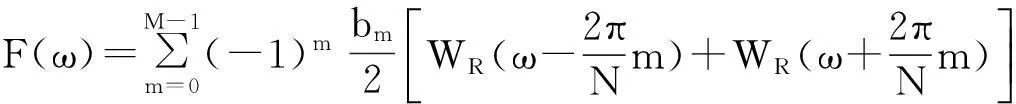
(9)

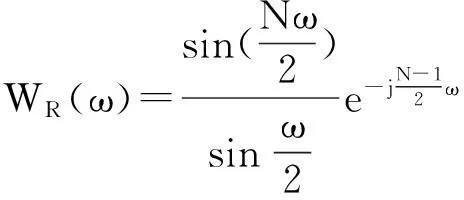
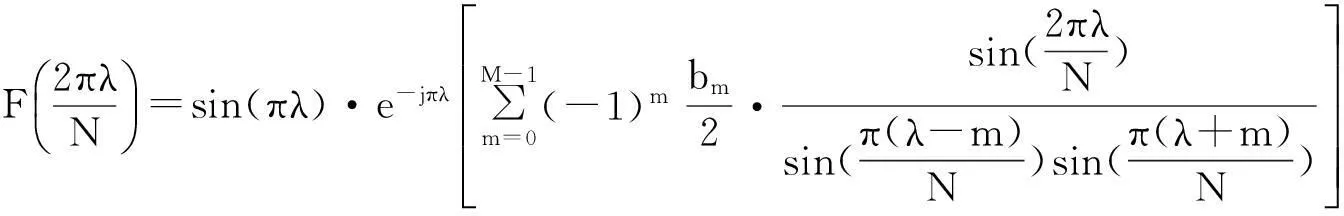
(10)

那么，当λ≪N时,式(10)可以简化为

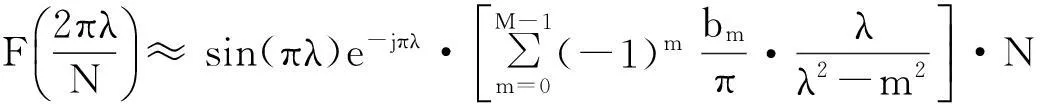
(11)

其幅度谱

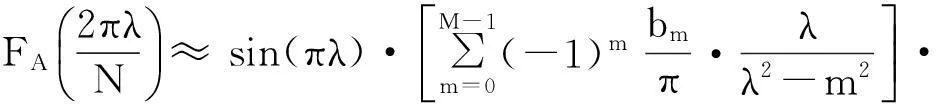
(12)

由于apFFT一般采用归一化的窗函数[11]，其幅度谱也应进行归一化处理.因此,对式(12)除以FA(0)进行归一化，而

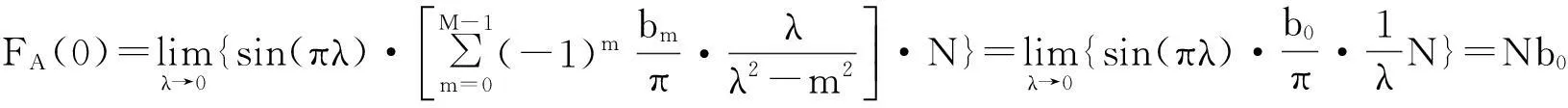
所以,式(12)除以Nb0即得归一化的幅度谱：

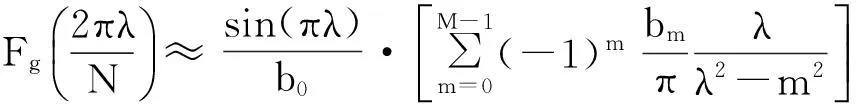
(13)

对于3项MSLD窗，将其系数代入式(13)并化简可得

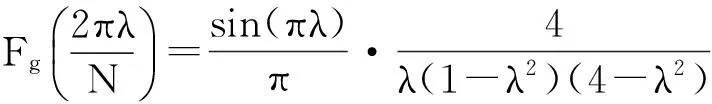
(14)

对于4项MSLD窗，将其系数代入式(13)并化简可得

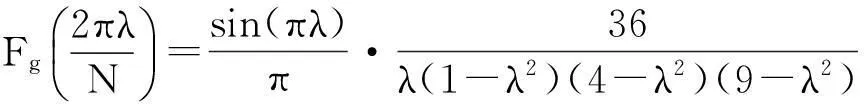
(15)

利用式(14)和(15)即可修正信号幅值，为此对式(7)进一步化简,由于

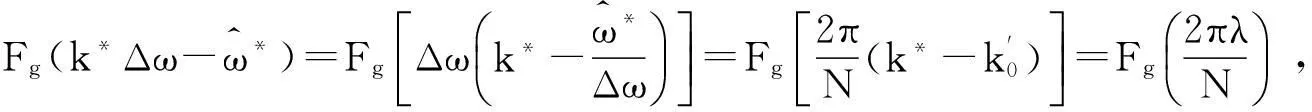
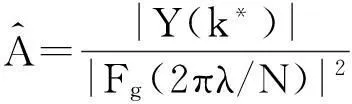
(16)

将式(14)和(15)分别代入式(16)可得3项MSLD窗双窗apFFT幅值修正公式与4项MSLD窗双窗apFFT幅值修正公式：

(17)

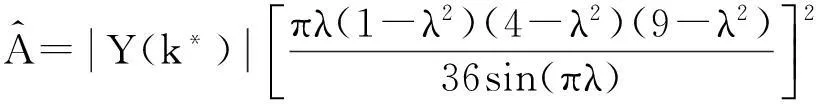
(18)

需要注意，以上的校正公式是针对式(3)的复单频信号，实际信号一般为实信号.由于实信号的频谱是双边谱，根据式(17)和(18)计算出的信号幅值是实际信号幅值的一半，故对于实信号，幅值的校正公式应对应乘以2.

4算法在电力系统谐波分析中的应用

基于MSLD窗的双窗apFFT算法具有优良的频谱泄露抑制能力，能获得较高的电力系统谐波分析精度.为了检验算法的实用效果，在Matlab中进行了仿真，采用的信号模型如下：

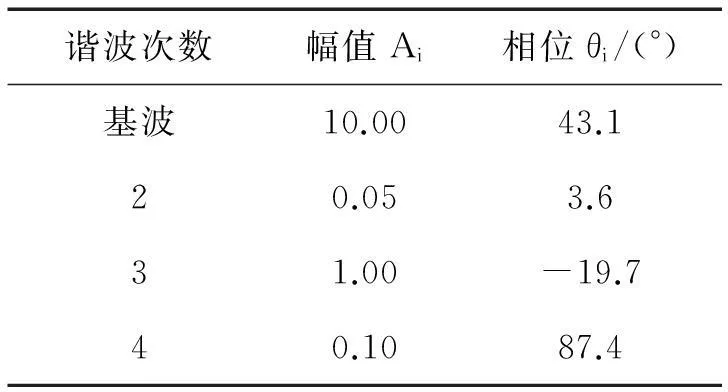
表2　仿真信号构成 Tab.2　Components of the simulated signal

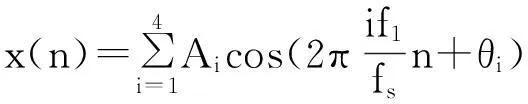
式中, f1为基波频率，各信号成分构成如表2所示.仿真中,采样频率fs取2 500 Hz，FFT的数据长度N取256 点，对应截断数据长度2N-1=511(近似10个工频周期)，两段序列的间隔L取1.

首先,检验算法的测频精度.让基波频率f1从49 Hz以0.1 Hz步进至51 Hz，各分量幅值和相位不变，按全相位FFT时移相位差法计算信号的基波频率f1，图2反映了f1变化时MSLD窗的双窗apFFT对应的f1计算精度.

从图2可以看出，3项和4项MSLD窗的基波频率测量精度均达到了10-8，4项MSLD窗的精度略优于3项MSLD窗.这与窗函数的旁瓣峰值和衰减速度有关，旁瓣峰值越低、衰减速度越快的窗函数抑制泄漏的效果越好、频率测量的精度越高.不过，在实际应用中还应考虑频谱分辨率，如果信号频率接近而频谱分辨率较高，主瓣较宽的MSLD窗可能不能分辨这样的谐波成分而导致频谱混叠，严重影响分析精度，这时应选择主瓣较窄的MSLD窗.

下面的仿真检验算法选择幅值较弱的2次谐波信号为考察对象，同样将基波频率f1从49 Hz以1 Hz步进至51 Hz对2次谐波产生不同程度的频谱干扰.仿真中，先对同样的两段采样序列分别进行3项和4项MSLD窗的双窗apFFT，之后按时移相位差法计算2次谐波的频率(2f1)，最后利用前面推导的幅值校正公式计算2次谐波的幅值，得到的幅值误差见图3.

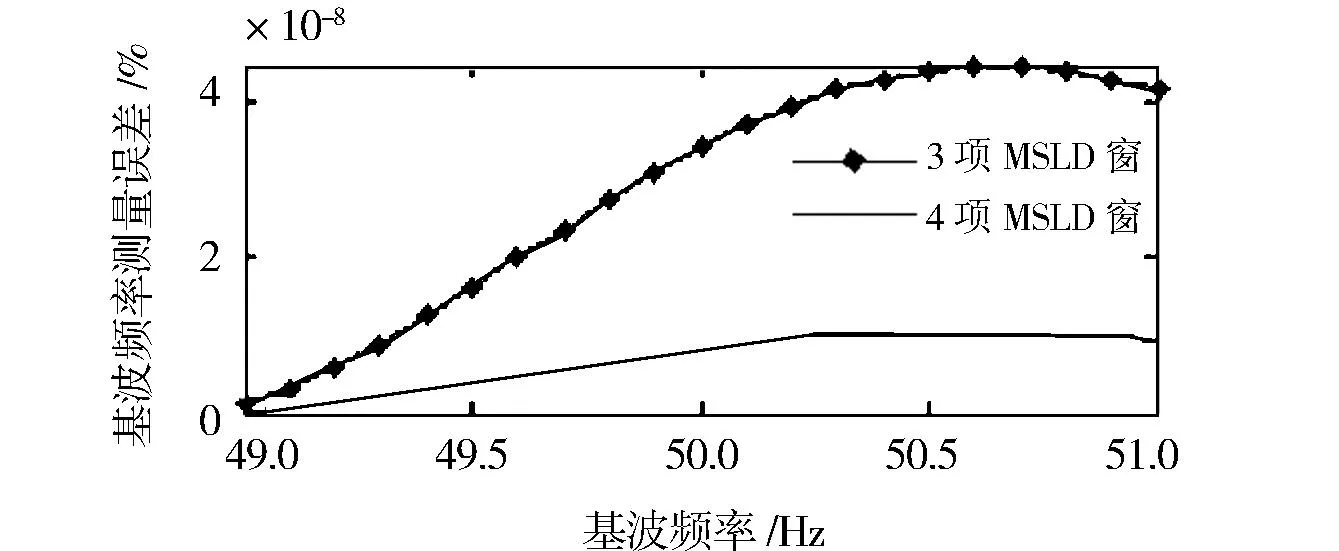
图2　基波频率测量误差 Fig.2　Relative errors in calculating fundamental frequency

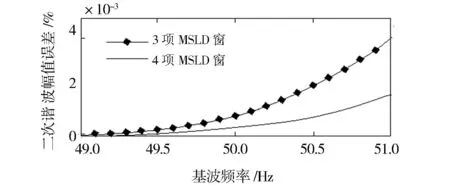
图3　二次谐波幅值测量误差 Fig.3　Relative errors in calculating secondary harmonic amplitude

从图3中可以看出，即使对容易被干扰的弱谐波成分，利用MSLD窗的双窗apFFT相位差法测量其幅值，也能达到较高精度.另外，与频率测量误差类似，旁瓣峰值越低、衰减速度越快的MSLD窗抑制泄漏的效果越好、幅值测量精度也越高.

apFFT的相位检测非常方便，因为apFFT无须校正就可以得到采样数据中心点的相位，同样以2次谐波为测试对象，图4反映了基波频率f1变动时2次谐波的相位检测误差.

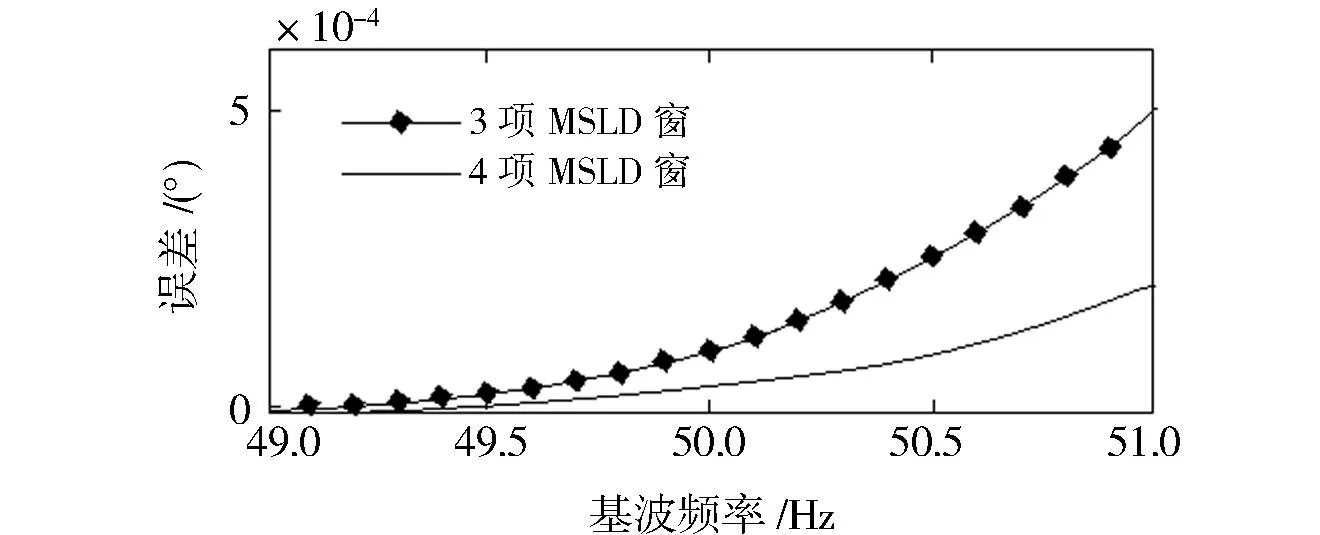
图4　二次谐波相位测量误差 Fig.4　Errors in calculating secondary harmonic phase

从图4中可以看出，MSLD窗的双窗apFFT相位检测精度也较高.同样，项数越大的MSLD窗泄漏抑制效果越好、测量精度越高.

综合以上仿真结果可以看出，基于MSLD窗的双窗apFFT对信号频率、相位、幅值的检测精度均较高，可完成高精度的电力谐波分析；在满足频谱分辨率要求的前提下，采用项数较大的MSLD窗有利于获得更好的抑制泄漏效果、提高谐波分析的精度.

5结论

基于MSLD窗的双窗全相位FFT频谱分析算法将MSLD窗应用于apFFT中，具有良好的频谱泄漏抑制能力，所推导的幅值校正公式形式简洁、实现方便.该算法具有高精度的频率、相位和幅值检测能力，可应用于电力系统谐波分析等需要对信号进行高精度频谱分析的场合.

参考文献：

[1]吕润如.电力系统高次谐波[M].北京:中国电力出版社,1998.

[2]朱小勇,丁康.离散频谱校正方法的综合比较[J].信号处理,2001,17(1):91-97.

[3]王兆华,侯正信,苏飞.全相位FFT 频谱分析[J].通信学报,2003,24(11A):16-19.

[4]黄翔东,王兆华.全相位DFT抑制谱泄漏原理及其在频谱校正中的应用[J].天津大学学报：自然科学版,2007,40(7):574-578.

[5]黄翔东,王兆华.全相位时移相位差频谱校正法[J].天津大学学报：自然科学版,2008,41(7):815-820.

[6]秦小屿,陈卫泽.全相位FFT算法在机械传动测试系统中的应用[J].电讯技术,2010,50(5):117- 120.

[7]董翠英.基于DSP的全相位FFT频率计设计[J].制造业自动化,2012,34(7):138-140.

[8]黄深喜,樊晓平,刘少强,等.用于谐波分析的最大旁瓣衰落速度优化组合余弦窗函数[J].信息与控制,2010,39(4):435-440.

[9]黄翔东.全相位数字信号处理[D].天津:天津大学,2006.

[10]卿柏元,滕召胜，高云鹏,等.基于Nuttall窗双谱线插值FFT的电力谐波分析方法[J].中国电机工程学报，2008,28(25):153-158.

[11]王兆华,黄翔东.数字信号全相位谱分析与滤波技术[M].北京:电子工业出版社,2009.

Spectral analysis based on all-phase FFT with maximum

side lobe decay speed windows

CAI Xiaofeng1, XIONG Xin2

(1.CollegeofMechanicalEngineering,HenanInstituteofEngineering,Zhengzhou451191,China;

2.CollegeofElectricalInformationEngineering,HenanInstituteofEngineering,Zhengzhou451191,China)

Abstract:Fourier analysis is commonly used in power harmonic analysis. However, spectrum leakage problem exists in this method when the sampling is asynchronous, in this case the detection accuracy decreases seriously. In order to restrain spectrum leakage and enhance the precision, the all-phase FFT based on the maximum side lobe decay speed windows(short for MSLD windows) is proposed for power harmonic analysis, which can take the advantage of the MSLD windows' fast side lobe decay speed and the good ability of apFFT to restrain spectrum leakage. The convenient harmonic magnitude analysis formula of proposed algorithm is derived. Matlab simulation verifies that the proposed method has the good ability to restrain spectrum leakage and high precision for harmonic analysis．

Key words: all-phase; Fast Fourier Transform(FFT); window functions; interpolation; harmonic analysis